Abstract
We demonstrate here that cold antihydrogen beams formed and extracted from a cusp magnet (anti-Helmholtz coils) are well focused and spin-polarized. A new discovery was the fact that the antihydrogen beam follows the well-known lens formula of optical lenses with its focal length properly scaled with the initial kinetic energy, the magnetic field strength and the magnetic moment. Furthermore, the simulation revealed that for a certain kinetic energy region of antihydrogen atoms, the optimum production position is upstream of the center of the cusp magnet, where a well-known nested potential configuration can be applied.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The CPT (C: charge conjugation, P: parity operation, T: time reversal) symmetry is assumed to be the most fundamental symmetry in physics, and guarantees that atomic properties of antihydrogen ( ) and hydrogen are exactly the same. This symmetry might be violated if, for example, the gravitational interaction is taken into account, which causes the space-time to be curved [1]. The standard model extension developed by Kostelecky et al discusses physical quantities which are sensitive to the CPT violation [2]. High-precision comparisons of hyperfine transitions between
) and hydrogen are exactly the same. This symmetry might be violated if, for example, the gravitational interaction is taken into account, which causes the space-time to be curved [1]. The standard model extension developed by Kostelecky et al discusses physical quantities which are sensitive to the CPT violation [2]. High-precision comparisons of hyperfine transitions between  and hydrogen atoms are predicted to constitute stringent tests of the CPT violation [3].
and hydrogen atoms are predicted to constitute stringent tests of the CPT violation [3].
Syntheses of  atoms have been extensively studied in the last few decades. The ALPHA and the ATRAP collaborations aim at 1S–2S high-precision laser spectroscopy of
atoms have been extensively studied in the last few decades. The ALPHA and the ATRAP collaborations aim at 1S–2S high-precision laser spectroscopy of  atoms trapped in magnetic bottles [4, 5]. The ASACUSA collaboration attempts the CPT test through high-precision microwave spectroscopy of ground-state hyperfine transitions using
atoms trapped in magnetic bottles [4, 5]. The ASACUSA collaboration attempts the CPT test through high-precision microwave spectroscopy of ground-state hyperfine transitions using 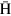 beams extracted in a magnetic field-free region [6–8].
beams extracted in a magnetic field-free region [6–8].
Recently, the ASACUSA collaboration successfully synthesized 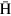 atoms in a so-called cusp trap, which is a unique method of preparing a spin-polarized
atoms in a so-called cusp trap, which is a unique method of preparing a spin-polarized  beam for a microwave spectroscopy of
beam for a microwave spectroscopy of 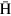 atoms, and produced
atoms, and produced  atomic beams [9, 10]. Figure 1 shows a conceptual drawing of the experimental setup, which is composed of the cusp trap, a microwave cavity, a sextupole magnet and an
atomic beams [9, 10]. Figure 1 shows a conceptual drawing of the experimental setup, which is composed of the cusp trap, a microwave cavity, a sextupole magnet and an 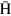 detector. The cusp trap consists of superconducting anti-Helmholtz coils and a stack of multiple ring electrodes (MRE).
detector. The cusp trap consists of superconducting anti-Helmholtz coils and a stack of multiple ring electrodes (MRE).  atoms formed in the cusp trap are emitted in all directions under the influence of the cusp magnetic field. As discussed in detail in the next section,
atoms formed in the cusp trap are emitted in all directions under the influence of the cusp magnetic field. As discussed in detail in the next section,  atoms in low-field-seeking states (LFS) are preferentially focused along the magnet axis, and a spin-polarized
atoms in low-field-seeking states (LFS) are preferentially focused along the magnet axis, and a spin-polarized  beam is automatically produced. It is noted that the magnetic bottle to trap
beam is automatically produced. It is noted that the magnetic bottle to trap  atoms [11, 12] employs a strong non-uniform magnetic field, which deteriorates the spectroscopic behavior of
atoms [11, 12] employs a strong non-uniform magnetic field, which deteriorates the spectroscopic behavior of  atoms. To avoid this problem, we designed the cusp trap scheme to extract
atoms. To avoid this problem, we designed the cusp trap scheme to extract 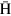 atoms from the cusp magnet region to a magnetic field-free region where a weak uniform magnetic field is easily prepared for high-precision microwave spectroscopy. Conventionally it is necessary to place a spin selector downstream of the
atoms from the cusp magnet region to a magnetic field-free region where a weak uniform magnetic field is easily prepared for high-precision microwave spectroscopy. Conventionally it is necessary to place a spin selector downstream of the 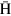 synthesizer to produce polarized beams, which are well integrated into the cusp trap, realizing efficient productions of polarized beams [13]. The
synthesizer to produce polarized beams, which are well integrated into the cusp trap, realizing efficient productions of polarized beams [13]. The 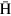 beam in LFS passes through the microwave cavity and is refocused on the
beam in LFS passes through the microwave cavity and is refocused on the  detector by the sextupole magnet. If the microwave frequency matches with one of the hyperfine transition frequencies, the
detector by the sextupole magnet. If the microwave frequency matches with one of the hyperfine transition frequencies, the  atoms in LFS are converted into high-field-seeking states (HFS). Because
atoms in LFS are converted into high-field-seeking states (HFS). Because 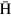 atoms in HFS are defocused by the sextupole magnet, most of them do not reach the
atoms in HFS are defocused by the sextupole magnet, most of them do not reach the  detector; i.e., the transition frequencies are precisely determined by measuring the number of
detector; i.e., the transition frequencies are precisely determined by measuring the number of  atoms reaching the
atoms reaching the  detector as a function of the microwave frequency.
detector as a function of the microwave frequency.
Figure 1. Schematic diagram for the ground-state hyperfine transition measurements of  atoms using the cusp trap, the microwave cavity, the sextupole magnet and the
atoms using the cusp trap, the microwave cavity, the sextupole magnet and the  detector.
detector.
Download figure:
Standard image High-resolution imageWe report here novel properties of the cusp magnet in transporting  beams; namely that the
beams; namely that the  atoms in LFS produced in the cusp trap are extracted along the magnet axis following a well-known lens formula for a broad range of experimental conditions.
atoms in LFS produced in the cusp trap are extracted along the magnet axis following a well-known lens formula for a broad range of experimental conditions.
2. Trajectory calculations of  beams
beams
The force acting on an 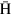 atom in a magnetic field
atom in a magnetic field  is given by
is given by  , where
, where  is the magnetic moment of the
is the magnetic moment of the 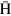 atom. In the magnetic field, the energy level of the
atom. In the magnetic field, the energy level of the 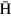 atom in the ground state splits into four sub-states. For a strong magnetic field,
atom in the ground state splits into four sub-states. For a strong magnetic field,  is approximately constant for all the four hyperfine states, and the forces are given by
is approximately constant for all the four hyperfine states, and the forces are given by 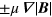 depending on whether
depending on whether 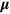 is parallel (HFS) or antiparallel (LFS) to
is parallel (HFS) or antiparallel (LFS) to 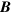 , respectively. In the following discussions, this strong magnetic field condition is assumed for the sake of simplicity.
, respectively. In the following discussions, this strong magnetic field condition is assumed for the sake of simplicity.
The above consideration is valid as far as the magnetic moment  of the
of the  atom adiabatically follows
atom adiabatically follows  . Such an adiabatic condition might not be satisfied near the center of the cusp magnet where
. Such an adiabatic condition might not be satisfied near the center of the cusp magnet where 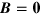 , and
, and  of the
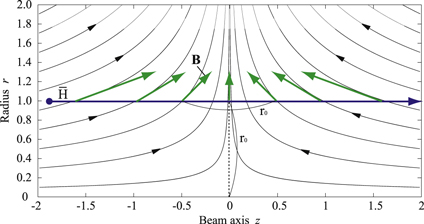
of the  atom makes a transition, which is called the Majorana spin-flip [15]. The criterion for the Majorana spin-flip can be obtained carefully as follows. The axial and radial magnetic fields of the cusp magnet near the center are given by
atom makes a transition, which is called the Majorana spin-flip [15]. The criterion for the Majorana spin-flip can be obtained carefully as follows. The axial and radial magnetic fields of the cusp magnet near the center are given by 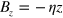 and
and 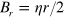 , respectively, where η is around 36 [T/m] in the case of the cusp magnet of the ASACUSA collaboration. The direction of
, respectively, where η is around 36 [T/m] in the case of the cusp magnet of the ASACUSA collaboration. The direction of 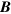 acting on the
acting on the 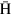 atom is shown along the trajectory passing near z = 0 at
atom is shown along the trajectory passing near z = 0 at  in figure 2. The time necessary to vary the direction by 1 radian would be evaluated by
in figure 2. The time necessary to vary the direction by 1 radian would be evaluated by 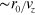 , where
, where  is the axial velocity of the
is the axial velocity of the 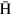 atom. Because the Larmor frequency is
atom. Because the Larmor frequency is 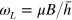 , if
, if 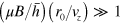 ,
,  is expected to follow the direction of
is expected to follow the direction of 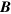 adiabatically. For example, when
adiabatically. For example, when 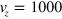 [m/s] (∼50 K),
[m/s] (∼50 K), 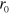 is estimated to be
is estimated to be 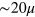 m for the ground state adopting the minimum
m for the ground state adopting the minimum 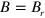 . Considering that the maximum radial position of the
. Considering that the maximum radial position of the  atoms at z = 0 reaching the cavity is about 5 mm (see the next paragraph), the fraction to make the Majorana spin-flip is about
atoms at z = 0 reaching the cavity is about 5 mm (see the next paragraph), the fraction to make the Majorana spin-flip is about  or less, which is negligibly small.
or less, which is negligibly small.
Figure 2. Magnetic field lines of the cusp magnet around the center where the 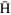 atom passes through the position z = 0.
atom passes through the position z = 0.
Download figure:
Standard image High-resolution imageTrajectories of  atoms in the cusp magnetic field are calculated solving the Newtonian equations of motion numerically. Initial emission directions of
atoms in the cusp magnetic field are calculated solving the Newtonian equations of motion numerically. Initial emission directions of 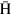 atoms are assumed to be isotropic. The z component of the magnetic field,
atoms are assumed to be isotropic. The z component of the magnetic field, 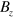 , of the model cusp magnet is drawn in figure 3(a). Figures 3(b) and (c) show examples of trajectories of
, of the model cusp magnet is drawn in figure 3(a). Figures 3(b) and (c) show examples of trajectories of 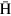 atoms in ground states having the initial kinetic energy of
atoms in ground states having the initial kinetic energy of  K synthesized at the maximum magnetic field,
K synthesized at the maximum magnetic field, 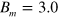 T, for LFS and HFS, respectively (
T, for LFS and HFS, respectively (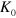 is given as a temperature unit, i.e., the kinetic energy divided by Boltzmannʼs constant). It is seen that the number of
is given as a temperature unit, i.e., the kinetic energy divided by Boltzmannʼs constant). It is seen that the number of  atoms in LFS traveling along the magnet axis is much larger than that in HFS; i.e., one can obtain an intensified and spin-polarized
atoms in LFS traveling along the magnet axis is much larger than that in HFS; i.e., one can obtain an intensified and spin-polarized  beam automatically. The 10 cm disk 1.5 m downstream from the cusp magnet center actually corresponds to the size and the position of the entrance of the microwave cavity in the ASACUSA setup (see figure 1).
beam automatically. The 10 cm disk 1.5 m downstream from the cusp magnet center actually corresponds to the size and the position of the entrance of the microwave cavity in the ASACUSA setup (see figure 1).
Figure 3. (a) The z component of the magnetic field,  , of the model cusp magnet. (b) Trajectories of
, of the model cusp magnet. (b) Trajectories of 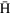 atoms in LFS synthesized on the magnet axis at the maximum magnetic field
atoms in LFS synthesized on the magnet axis at the maximum magnetic field 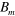 having the kinetic energy of
having the kinetic energy of 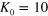 K. The open circle in (b) shows the
K. The open circle in (b) shows the  production position. The disk with its diameter of 10 cm placed at z = 1.5 m shows the size and the position of the entrance of the ASACUSA microwave cavity (see figure 1). Initial emission directions are assumed to be isotropic, and the lines are drawn every 1 degree from the beam axis. (c) The same as (b) but for
production position. The disk with its diameter of 10 cm placed at z = 1.5 m shows the size and the position of the entrance of the ASACUSA microwave cavity (see figure 1). Initial emission directions are assumed to be isotropic, and the lines are drawn every 1 degree from the beam axis. (c) The same as (b) but for  atoms in HFS.
atoms in HFS.
Download figure:
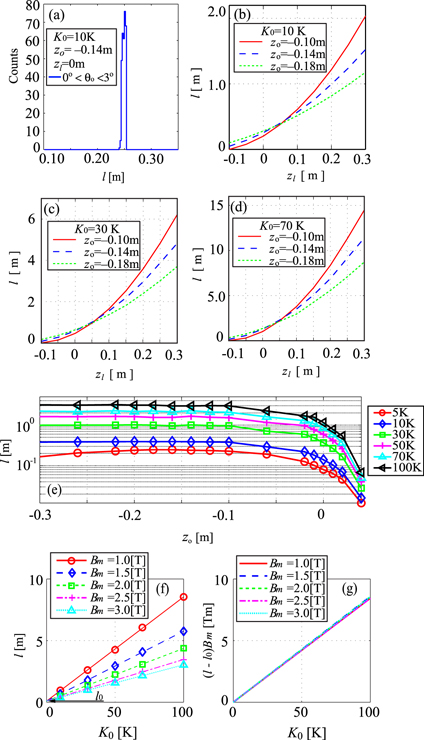
Standard image High-resolution imageFigure 4(a) again shows 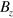 . Symbols in figures 4(b) and (c) plot the fractions of LFS (
. Symbols in figures 4(b) and (c) plot the fractions of LFS ( ) and HFS (
) and HFS ( )
)  atoms reaching the 10 cm disk, calculated solving the equations of motion as a function of the
atoms reaching the 10 cm disk, calculated solving the equations of motion as a function of the 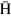 production position,
production position,  , respectively. Different symbols correspond to different kinetic energies,
, respectively. Different symbols correspond to different kinetic energies,  , from 5 K to 100 K. The thick blue solid lines in figures 4(b) and (c) show the fraction of
, from 5 K to 100 K. The thick blue solid lines in figures 4(b) and (c) show the fraction of 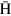 atoms arriving at the disk when
atoms arriving at the disk when  atoms are emitted isotropically following straight trajectories (the solid angle divided by
atoms are emitted isotropically following straight trajectories (the solid angle divided by  from
from  to the 10 cm disk). For all the temperatures calculated, the fractions of
to the 10 cm disk). For all the temperatures calculated, the fractions of 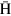 atoms in LFS transported to the disk are larger than the fraction of the straight trajectory case for
atoms in LFS transported to the disk are larger than the fraction of the straight trajectory case for 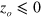 m; i.e.,
m; i.e.,  beams in LFS are focused. In the case of
beams in LFS are focused. In the case of 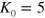 K and 10 K (the red open circles and blue open diamonds, respectively), the fraction increases considerably for smaller
K and 10 K (the red open circles and blue open diamonds, respectively), the fraction increases considerably for smaller 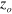 . In other words, the best position to synthesize
. In other words, the best position to synthesize  atoms is located upstream of the cusp magnet center, although synthesis at the center was anticipated in the original cusp trap scheme [13]. This is particularly true because the densities of antiproton and positron plasmas are higher at the higher magnetic field, resulting in a higher
atoms is located upstream of the cusp magnet center, although synthesis at the center was anticipated in the original cusp trap scheme [13]. This is particularly true because the densities of antiproton and positron plasmas are higher at the higher magnetic field, resulting in a higher  yield. Actually, the first
yield. Actually, the first  production in the cusp trap was realized at the maximum magnetic field region taking this optimal property into account [9, 10]. In the case of
production in the cusp trap was realized at the maximum magnetic field region taking this optimal property into account [9, 10]. In the case of  ,
, 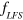 reaches its maximum at
reaches its maximum at  m (with the intensity enhancement of ∼ 200), because 5 K
m (with the intensity enhancement of ∼ 200), because 5 K 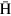 atoms produced at
atoms produced at 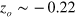 m are focused on the disk 1.5 m downstream of the cusp magnet. For
m are focused on the disk 1.5 m downstream of the cusp magnet. For  ,
, 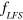 is almost constant, independent of
is almost constant, independent of 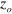 . This finding suggests that
. This finding suggests that 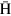 atoms in a certain kinetic energy range can be synthesized in a strong magnetic field region, where a well-known nested potential configuration [14] can be applied, still optimizing the
atoms in a certain kinetic energy range can be synthesized in a strong magnetic field region, where a well-known nested potential configuration [14] can be applied, still optimizing the  beam intensity. For
beam intensity. For  atoms in HFS in figure 4(c), the behavior is just the opposite: the lower the kinetic energy, the lower the transport efficiency; i.e., the cusp magnetic field acts in itself as the spin filter as well as the beam intensifier of
atoms in HFS in figure 4(c), the behavior is just the opposite: the lower the kinetic energy, the lower the transport efficiency; i.e., the cusp magnetic field acts in itself as the spin filter as well as the beam intensifier of  atoms in LFS. Figure 4(d) shows the polarization of
atoms in LFS. Figure 4(d) shows the polarization of  beams calculated using the results of figures 4(b) and (c) assuming that an equal number of LFS and HFS are produced, where the polarization is defined by
beams calculated using the results of figures 4(b) and (c) assuming that an equal number of LFS and HFS are produced, where the polarization is defined by 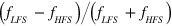 . The polarization decreases gradually as
. The polarization decreases gradually as 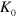 increases.
increases.
Figure 4. (a) 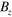 on axis. The different symbols in (b) and (c) correspond to the calculated transport fraction of
on axis. The different symbols in (b) and (c) correspond to the calculated transport fraction of 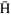 atoms in LFS and HFS reaching the 10 cm disk, solving the equations of motion as a function of the production position
atoms in LFS and HFS reaching the 10 cm disk, solving the equations of motion as a function of the production position  . The curves in (b) and (c) correspond to the transport fraction evaluated using equations (1) and (5) (see the text for details), respectively. (d) The spin-polarization of
. The curves in (b) and (c) correspond to the transport fraction evaluated using equations (1) and (5) (see the text for details), respectively. (d) The spin-polarization of 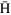 atoms reaching the disk.
atoms reaching the disk.
Download figure:
Standard image High-resolution image3. Lens formula and the scaling law
Having observed that the cusp magnet has the ability to enhance the beam intensity of 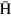 atoms in LFS, the next step is to quantitatively study the transport property. In doing so, the image point,
atoms in LFS, the next step is to quantitatively study the transport property. In doing so, the image point,  , is evaluated calculating trajectories with different ejection angles,
, is evaluated calculating trajectories with different ejection angles,  , from the axis at a fixed object point (
, from the axis at a fixed object point ( production position
production position 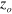 ). Then, the thin lens formula,
). Then, the thin lens formula, 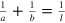 , is applied to get the focal length l, where a and b are given by
, is applied to get the focal length l, where a and b are given by 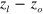 and
and  , respectively, and
, respectively, and 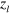 is an effective lens position. Figure 5(a) shows the example of l evaluated using
is an effective lens position. Figure 5(a) shows the example of l evaluated using  for 10 K
for 10 K 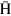 atoms in LFS produced at
atoms in LFS produced at  m assuming
m assuming 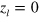 m for
m for 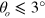 . It is observed that for different ejection angles, l is distributed in a narrow region for a fixed
. It is observed that for different ejection angles, l is distributed in a narrow region for a fixed 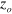 ; i.e., the concept of the focal length is well satisfied. In the following, the central value of l for
; i.e., the concept of the focal length is well satisfied. In the following, the central value of l for  atoms arriving at the disk is re-defined as the focal length l. Figure 5(b) shows l evaluated as a function of
atoms arriving at the disk is re-defined as the focal length l. Figure 5(b) shows l evaluated as a function of  for 10 K
for 10 K 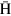 atoms (
atoms (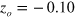 ,
, 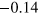 and
and 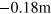 ). Figures 5(c) and (d) are the same as figure 5(b) but for
). Figures 5(c) and (d) are the same as figure 5(b) but for 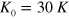 and 70 K, respectively. It is observed that l can be determined consistently independent of
and 70 K, respectively. It is observed that l can be determined consistently independent of  for each
for each  if
if 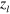 is chosen to be ∼0.05 m; i.e., the cusp magnet acts practically as a converging lens for
is chosen to be ∼0.05 m; i.e., the cusp magnet acts practically as a converging lens for  beams in LFS, fulfilling the lens formula with a small aberration. Figure 5(e) shows l as a function of
beams in LFS, fulfilling the lens formula with a small aberration. Figure 5(e) shows l as a function of 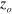 for 5 K
for 5 K 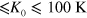 , setting
, setting 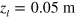 . l is almost constant for
. l is almost constant for 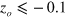 m for each
m for each 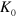 . Figure 5(f) shows l as a function of
. Figure 5(f) shows l as a function of  for five different
for five different  with
with 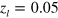 m, where l is evaluated, e.g., from figure 5(e) for
m, where l is evaluated, e.g., from figure 5(e) for 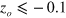 m in the case of
m in the case of 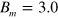 T, and the lines are drawn employing the linear least square method. It is seen that l increases linearly with
T, and the lines are drawn employing the linear least square method. It is seen that l increases linearly with 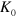 , having a steeper slope for a lower
, having a steeper slope for a lower 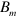 . Furthermore, all lines merge at the same point when
. Furthermore, all lines merge at the same point when  is extrapolated to 0 with a finite intercept,
is extrapolated to 0 with a finite intercept,  0.09 m. Figure 5(g) plots
0.09 m. Figure 5(g) plots 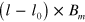 as a function of
as a function of 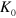 . All the lines overlap with each other; i.e., l has an excellent scaling property with respect both to
. All the lines overlap with each other; i.e., l has an excellent scaling property with respect both to  and to
and to 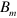 :
:
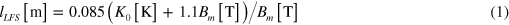
for  atoms in LFS (
atoms in LFS (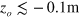 ). Because we know the lens position,
). Because we know the lens position,  , as well as l,
, as well as l,  and
and  , the transport fraction of
, the transport fraction of  atoms to the 10 cm disk is easily calculated, and is shown by the lines in figure 4(b). These lines are in good agreement with results obtained by numerical simulations (symbols in figure 4(b)).
atoms to the 10 cm disk is easily calculated, and is shown by the lines in figure 4(b). These lines are in good agreement with results obtained by numerical simulations (symbols in figure 4(b)).
Figure 5. (a) The focal length distribution of 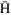 atoms in LFS evaluated using the relation
atoms in LFS evaluated using the relation 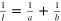 for the ejection angle of
for the ejection angle of 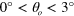 . (b), (c) and (d) The focal length l for
. (b), (c) and (d) The focal length l for  atoms in LFS as a function of
atoms in LFS as a function of 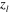 for three different
for three different  for
for 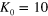 , 30 and 70 K. (e) The focal length l as a function of
, 30 and 70 K. (e) The focal length l as a function of  for
for 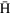 atoms in LFS with
atoms in LFS with  . (f) The focal length l as a function of
. (f) The focal length l as a function of 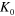 for
for 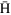 atoms in LFS with
atoms in LFS with 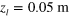 for five different
for five different 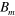 . (g)
. (g) 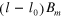 as a function of
as a function of  for
for 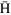 atoms in LFS with
atoms in LFS with 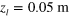 .
.
Download figure:
Standard image High-resolution image4. Qualitative analysis of the property of the cusp magnet
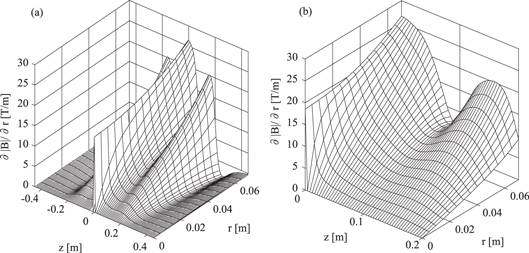
To understand why the lens formula is applicable to the cusp magnet, which is quadrupolar in its nature but not sextupolar, the behavior of the magnetic field of the cusp magnet is studied in detail. The focusing property is primarily determined by the radial force acting on the beam; i.e.  for
for  atoms in LFS. Figure 6(a) shows
atoms in LFS. Figure 6(a) shows 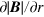 , and figure 6(b) is a closeup for 0 m
, and figure 6(b) is a closeup for 0 m 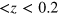 m. When
m. When 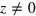 ,
, 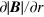 is 0 at r = 0 and increases monotonically with r for
is 0 at r = 0 and increases monotonically with r for  m (actually the inner radius of the MRE in the ASACUSA setup is 0.04 m). Although
m (actually the inner radius of the MRE in the ASACUSA setup is 0.04 m). Although  is almost constant with respect to r at z = 0, this is just a singular point. Taking e.g.
is almost constant with respect to r at z = 0, this is just a singular point. Taking e.g.  at z = 0.004 m (the curve closest to z = 0 in figure 6(b)), it increases more or less linearly for
at z = 0.004 m (the curve closest to z = 0 in figure 6(b)), it increases more or less linearly for 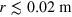 . As a whole,
. As a whole, 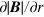 can be practically approximated as
can be practically approximated as 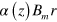 , where
, where 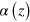 is a coefficient of the field gradient as a function of z. Accordingly, the radial force acting on the
is a coefficient of the field gradient as a function of z. Accordingly, the radial force acting on the 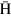 atom is given by
atom is given by 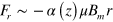 ; i.e., the cusp magnet here behaves like a sextupole magnet (
; i.e., the cusp magnet here behaves like a sextupole magnet ( ).
).
Figure 6. (a)  of the model cusp magnet. (b) The closeup of (a).
of the model cusp magnet. (b) The closeup of (a).
Download figure:
Standard image High-resolution imageThe change of the deflection angle,  , due to the radial momentum transfer from the magnetic field to the
, due to the radial momentum transfer from the magnetic field to the  atom is given by
atom is given by
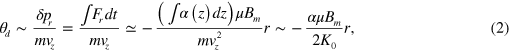
where m is the 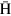 mass,
mass,  and
and 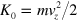 . In contrast to the direction, the radial position of
. In contrast to the direction, the radial position of  atoms does not vary very much during the deflection; therefore the trajectory of
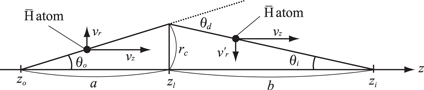
atoms does not vary very much during the deflection; therefore the trajectory of 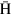 atoms can be approximated as in figure 7. In this case, the radial position of the
atoms can be approximated as in figure 7. In this case, the radial position of the 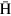 atom produced at
atom produced at 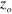 with its ejection angle
with its ejection angle 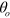 with respect to the axis is given by
with respect to the axis is given by  at
at  , and the angle at the image point,
, and the angle at the image point, 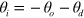 , is given by
, is given by 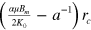 . In this case, all the trajectories meet at the same point at
. In this case, all the trajectories meet at the same point at 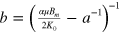 , independent of
, independent of 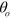 . Using a and b above, one can immediately obtain the focal length l as
. Using a and b above, one can immediately obtain the focal length l as  . Furthermore, the small correction appearing in equation (1) can be understood as the result of the acceleration of
. Furthermore, the small correction appearing in equation (1) can be understood as the result of the acceleration of 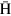 atoms in LFS by the magnetic field, which amounts to
atoms in LFS by the magnetic field, which amounts to  . By replacing
. By replacing 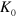 with
with 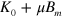 , one gets
, one gets
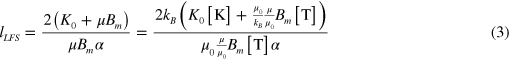

where  and
and  are the Bohr magneton and Boltzmannʼs constant, respectively. The third equation is obtained considering the size of the magnet (
are the Bohr magneton and Boltzmannʼs constant, respectively. The third equation is obtained considering the size of the magnet (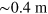 ) and
) and 
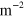 assuming
assuming 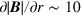 T/m at r = 0.04 m (figure 6(b)). For the ground state (
T/m at r = 0.04 m (figure 6(b)). For the ground state (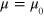 ), equation (4) is semi-quantitatively consistent with equation (1); i.e., the behavior of the cusp magnet is well understood. As shown in equation (3),
), equation (4) is semi-quantitatively consistent with equation (1); i.e., the behavior of the cusp magnet is well understood. As shown in equation (3), 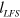 also has the scaling property with respect to μ.
also has the scaling property with respect to μ.
Figure 7. A schematic trajectory of the  atom in LFS approximating that the momentum transfer takes place only at
atom in LFS approximating that the momentum transfer takes place only at  .
.
Download figure:
Standard image High-resolution imageIn the case of 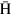 atoms in HFS, the direction of the force is just the opposite; i.e.,
atoms in HFS, the direction of the force is just the opposite; i.e., 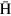 atoms are axially decelerated and radially defocused. Accordingly, by replacing
atoms are axially decelerated and radially defocused. Accordingly, by replacing  by
by 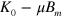 and
and  by
by  , and employing more correct coefficients obtained in equation (1), one gets
, and employing more correct coefficients obtained in equation (1), one gets
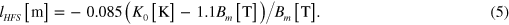
The transport fraction of 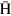 atoms in HFS can be evaluated in a similar way as in LFS, employing equation (5), which is shown by the lines in figure 4(c). It is seen that these lines reproduce the results of numerical simulations quite well. The polarization using
atoms in HFS can be evaluated in a similar way as in LFS, employing equation (5), which is shown by the lines in figure 4(c). It is seen that these lines reproduce the results of numerical simulations quite well. The polarization using 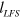 and
and  is also shown by the lines in figure 4(d), which again reproduces the numerical simulations quite well; i.e., the cusp magnet works as a magnetic lens for LFS and also for HFS
is also shown by the lines in figure 4(d), which again reproduces the numerical simulations quite well; i.e., the cusp magnet works as a magnetic lens for LFS and also for HFS  beams. It is also noted that the cusp magnet can be used as a good spin-selector for molecular beam experiments.
beams. It is also noted that the cusp magnet can be used as a good spin-selector for molecular beam experiments.
5. Conclusion
Here, we study the transport properties of cold 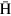 atoms produced in the cusp magnet. Although the cusp magnet (anti-Helmholtz coils) has in principle a quadrupolar field distribution, it is found that the
atoms produced in the cusp magnet. Although the cusp magnet (anti-Helmholtz coils) has in principle a quadrupolar field distribution, it is found that the  beams prepared upstream of the center of the cusp magnet are well characterized and follow the lens formula of optical lenses. The focal length satisfies a scaling law on the initial kinetic energy (
beams prepared upstream of the center of the cusp magnet are well characterized and follow the lens formula of optical lenses. The focal length satisfies a scaling law on the initial kinetic energy ( ), the maximum magnetic field strength(
), the maximum magnetic field strength(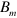 ) and the magnetic moment (μ) of
) and the magnetic moment (μ) of 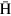 atoms. Because the cusp magnet focuses
atoms. Because the cusp magnet focuses 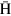 atoms in LFS along the magnet axis and defocuses those in HFS, one gets a spin-polarized intensified
atoms in LFS along the magnet axis and defocuses those in HFS, one gets a spin-polarized intensified 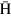 beam automatically.
beam automatically.
Furthermore, it is found that the best position to produce 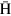 atoms for a stronger
atoms for a stronger  beam with higher polarization is upstream of the center of the cusp magnet for a broad range of
beam with higher polarization is upstream of the center of the cusp magnet for a broad range of 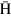 kinetic energy. This allows the use of the so-called nested trap configuration, which greatly simplifies the
kinetic energy. This allows the use of the so-called nested trap configuration, which greatly simplifies the  production procedures.
production procedures.