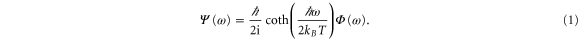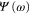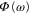Focus on nonequilibrium fluctuation relations: from classical to quantum

A central finding of equilibrium statistical physics is that fluctuations inevitably induce dissipation in a system with many degrees of freedom. This is the content of the well-known fluctuation-dissipation theorem. For a system at thermal equilibrium, it relates the fluctuations in the system with its dissipative response to sufficiently weak external perturbations. Historically, this connection was first observed by William Sutherland [1, 2] and Albert Einstein [3–5] for the relation between the mobility of a Brownian particle, which is a quantity that measures the response to an external electric field, and the diffusion constant, which is a quantity that characterizes the fluctuating forces at equilibrium. The resulting Einstein relation between the diffusion constant and temperature is of fundamental importance.

Yet another form is known as the Johnson–Nyquist relation [6, 7] for thermal charge fluctuations in an electrical resistor and the electrical resistance of a circuit regardless of any applied voltage. A generalized quantum relation, consistent with the second law of thermodynamics and the principle of detailed balance, has been derived by Callen and Welton [8] in form of the quantum fluctuation-dissipation theorem

$$\begin{eqnarray}&&\Psi (\omega )=\frac{\hbar }{2{\rm i}}{\rm coth} \left( \frac{\hbar \omega }{2{{k}_{B}}T} \right)\Phi (\omega ).\end{eqnarray} \tag{ 1 }$$

Here, the Fourier transform $\Psi (\omega )$ of the symmetric equilibrium correlation function of an observable is related to the Fourier transform $\Phi (\omega )$ of the antisymmetric response function of this observable in thermal equilibrium at temperature T. It was recognized by Green [9, 10] and Kubo [11] that the fluctuation-dissipation theorem is a special case of the general linear response theory. This formalism relates the quantities of the system which is perturbed out of thermal equilibrium only to quantities given at thermal equilibrium.

Clearly, the assumption of thermal equilibrium is often not appropriate, for example, for systems in strong external fields, charge currents in transport systems with large differences in the electrochemical potential, heat currents in systems with large temperature gradients, or systems strongly coupled to polar solvents and disordered media which themselves are in a metastable quasi-equilibrium only.

It is an interesting question how the equilibrium fluctuation dissipation theorem can be generalized for nonequilibrium situations. Generalized nonequilibrium fluctuation theorems have been formulated for classical nonstationary Markov processes [12] and for stationary Markov processes away from thermal equilibrium [13, 14]. They relate the higher-order nonlinear response to higher-order correlation functions of stationary nonequilibrium fluctuations. An exact universal nonlinear classical fluctuation relation has been provided by Bochkov and Kuzovlev [15]. It solely builds on the time-reversal invariance of the equations of motion and the assumption of a thermally equilibrated initial state. The quantum version was formulated by Andrieux and Gaspard [16] and led to fundamental insights into the fact that work injected to or extracted from a system is not a quantum mechanical operator or observable, because it characterizes a process rather than a state of the system [17]. An alternative formulation for the statistics of nonequilibrium fluctuations in steady states has been provided by Evans et al [18] and by Gallavotti and Cohen [19]. Moreover, Jarzynski [20] and Crooks [21] have formulated a corresponding relation for the statistics of work performed by a transient time-dependent perturbation. The reviews [22–28] give an overview in this field.

In this 'focus on' series, we have collected recent works to illustrate the present state of the art on nonequilibrium fluctuation relations from classical to quantum statistical physics. Fluctuation relations build on the fundamental connection between the response of a physical system to an externally applied force (which is not necessarily weak) to corresponding changes of equilibrium state functions. For classical nonequilibrium systems, the separation of the total entropy production into the adiabatic and nonadiabatic contributions is useful for understanding irreversibility. For driven open quantum systems, Horowitz and Parrondo [29] formulate quantum analogues in terms of quantum jump trajectories. A quantum formulation of the local detailed balance condition is found.

Then, Talkner et al [30] characterize the work which is performed on a system in a microcanonical state by changes in a control parameter in terms of transition probabilities between eigenstates of the system Hamiltonians at the beginning and the end of the parameter change. They obey a detailed balance-like relation from which various forms of the microcanonical fluctuation theorem are obtained. Verley et al [31] identify the conditions under which a stochastic driving that induces energy changes into a system coupled with a thermal bath can be treated as a work source. Then, the work statistics satisfy the Crooks fluctuation theorem which is traditionally derived for deterministic drivings.

A scheme of a calorimetric measurement of work in a quantum system is proposed by Pekola et al [32] for a Cooper-pair box driven by a gate voltage past an avoided level crossing at charge degeneracy. Then, the temperature measurement of a resistor (environment) can detect single microwave photons emitted or absorbed. By this method, the full distribution of work in repeated measurements can be measured, and, thus quantum fluctuation relations can be directly revealed.

The transient quantum fluctuation theorems of Crooks and Jarzynski restrict and relate the statistics of work performed in forward and backward forcing protocols. For these theorems, it has been assumed that the work is determined by two projective energy measurements, one at the end, and the other one at the beginning of each run of the protocol. Venkatesh et al have found [33] that one can replace these two projective measurements only by special error-free generalized energy measurements with pairs of tailored, protocol-dependent post-measurement states that satisfy detailed balance-like relations.

A nonthermal environment also can yield to nonequilibrium fluctuation relations. For the exactly analytically solvable case of a quantum harmonic oscillator in a nonthermal harmonic environment, Pagel et al [34] have derived nonequilibrium fluctuation relations. Moreover, Campisi [35] uses the canonical distribution of wave functions, as originally proposed by Schrödinger, to derive novel fluctuation relations. They do not involve any quantum collapse, but involve instead a notion of work as the change in the expectation value of the Hamiltonian.

Rahav and Jarzynski [36] argue that fluctuation theorems can be understood in terms of the equilibrium dynamics of a larger supersystem which contains both the system of interest and its thermal surroundings. By applying the principle of detailed balance to underlying rare events, they are able to recover the fluctuation theorem in both its transient and steady-state formulations.

Nonequilibrium entropy production can also be related to the information exchange between two stochastic systems. This is shown by Sagawa and Ueda [37] in terms of a general formula that decomposes the total entropy production into the thermodynamic and informational parts. Nonequilibrium equalities such as the fluctuation theorem in the presence of information processing are the result.

In contrast with the understanding of fluctuation symmetries for entropy production, Maes and Salazar [38] develop corresponding ideas for the time-symmetric fluctuation sector. They provide time-symmetric fluctuation symmetries in boundary-driven particle systems such as the open Kawasaki lattice gas and the zero-range model.

When a current flows across an open system in contact with several reservoirs at different temperatures and chemical potentials, or when a system is driven by time-independent external mechanical forces, general nonequilibrium fluctuations also arise. Gaspard [39] derives multivariate fluctuation relations for all the currents in the presence of several reservoirs at different temperatures and electrochemical potentials, or driven by time-independent external mechanical forces. A nonequilibrium quantum transport setup is also analyzed by Zazunov et al [40]. Several helical Luttinger liquid nanowires are coupled to a joint mesoscopic superconductor with finite charging energy. Including the Majorana bound states formed near the ends of superconducting wire parts, they derive and analyze the Keldysh phase action describing non-equilibrium charge transport properties of the junction.

A modulated nonlinear oscillator also provides the framework to study quantum fluctuations far away from thermal equilibrium. Peano and Dykman [41] address a simple but important nonequilibrium effect—quantum heating. Here, quantum fluctuations lead to a finite-width distribution of a resonantly modulated oscillator over its quasienergy (Floquet) states. They analyze large rare fluctuations responsible for the tail of the quasienergy distribution and switching between metastable states of forced vibrations.

An effectively driven nonequilibrium system is furthermore studied by Pigeon et al [42] in the form of three interacting spin $-1/2$, one of which is coupled to a harmonic oscillator. This effectively modulates the interactions between all of them. By using the large-deviation theory, they find a Gallavotti–Cohen symmetry in the dynamics of the system which involves a global rather than a local degree of freedom and which gives rise to a fluctuation relation associated to the quantum jump rate.

An efficient numerical method for obtaining Markovian equations of motion for a many body system of interacting coarse-grained variables and additional fluxes is introduced by Kauzlarić et al [43]. The system of Markovian equations of motion approximates Mori's exact non-Markovian generalized Langevin equation and is easy to solve by computer simulation.

We believe that the research assembled in this 'focus on' series provides an exciting account of the topic of nonequilibrium fluctuation relations. Such a collection can only be made possible by the contributing authors and we use this opportunity to thank them for their submissions. Likewise, we are grateful to all the reviewers for the their careful assessment of the manuscripts and their insightful advice during the review process. Finally, we are indebted to the publisher Elena Belsole for her support in launching this 'focus on' series.