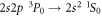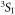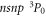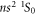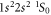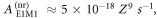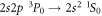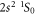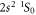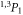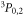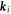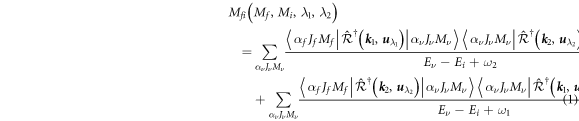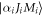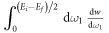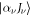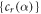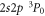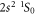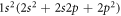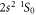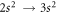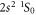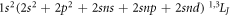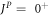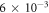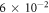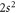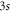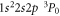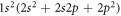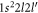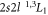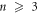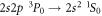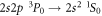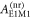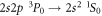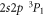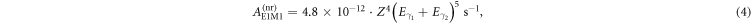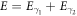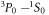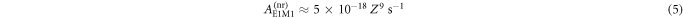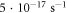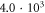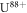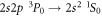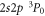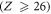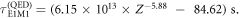Relativistically prolonged lifetime of the 2s2p³P₀ level of zero nuclear-spin beryllium-like ions

Since the beginning of atomic spectroscopy, metastable states have attracted much interest in studying electronic excitations in many-electron atoms and ions and their interaction with light and matter. Perhaps the two best known metastable states are the singlet and triplet 1s2s^1,3S levels of neutral helium with lifetimes of about 19 ms and ∼ 8000 s [1], but where the decay of the ${}^{3}{S}_{1}$ needs still to be measured accurately. The large differences in the lifetimes of these metastable levels arise from quantum-mechanical selection rules and the different coupling of the electronic density to the radiation field. For the ${}^{3}{S}_{1}$ level of helium, for instance, a simultaneous spin-flip of one of the electrons is required in order to allow a transition into the $1{s}^{2}{\;}^{1}{S}_{0}$ ground state. Apart from long-living atomic and ionic states, metastable levels are quite common in many branches of physics, including nuclear and molecular isomers, amorphous solids, the folding of proteins, or even metastable formations of macroscopic matter.

While transitions from metastable atomic states towards the ground level of the system are typically forbidden due to the well-known electric-dipole selection rule, these levels can often still decay by either higher-multipole or multi-photon transitions. For example, the helium ³S₁ level mentioned above decays via a single-photon magnetic-dipole transition at 62.5 nm or by a E1E1 two-photon process [1–3]. Both of these decay modes have been observed experimentally for various ions along the helium isoelectronic sequence [4–6] as well as in astrophysical sources [7]. Beside the analysis of the total rates, recent emphasis was placed also upon the angular emission and correlations of the two photons [8–11]. Only quite rarely, as for the ${nsnp}{\ }^{3}{P}_{0}$ levels of alkaline-Earth-like atoms and ions with zero nuclear spin, neither any single-photon nor E1E1 two-photon transition is possible, and such excited atoms must decay by an E1M1 (or by an even weaker 3E1) transition to the ${{ns}}^{2}{\ }^{1}{S}_{0}$ ground state in order to obey the inversion symmetry (parity) of isolated atoms. However, such weak decay channels are already not important for the quite analogous $1s2p{\ }^{3}{P}_{0}$ state of helium-like ions, which predominantly decays via a single-photon E1 transition to the $1s2s{\ }^{3}{S}_{1}$ level, though the relative importance of the alternative E1M1 transition mode increases with the nuclear charge Z [12, 13]. In practice, moreover, such strongly suppressed E1M1 transitions will become visible only for well-isolated atoms and isotopes with zero-nuclear spin, in which no single-photon transitions can be induced by hyperfine interactions or any external fields. When compared with the dipole-allowed E1E1 two-photon transitions, the simultaneous emission of an electric and magnetic dipole photon is suppressed by (at least) a factor ${\alpha }^{2}$ in the fine-structure constant and, indeed, no E1E1 forbidden two-photon decay process has yet been measured in the laboratory. For beryllium-like ions with non-zero nuclear spin, in contrast, the hyperfine-induced decay rates of the $2s2p{\ }^{3}{P}_{0}$ level have been calculated and explored in first laboratory measurements [14–17].

While, for the reasons given previously, pure E1M1 two-photon transitions are not relevant for helium-like ions, they form the only decay mode for the lowest-excited $1{s}^{2}2s2p{\ }^{3}{P}_{0}$ level of beryllium-like ions with zero nuclear-spin because of the necessary J = 0 → 0 transition into the $1{s}^{2}2{s}^{2}{\ }^{1}{S}_{0}$ ground state. First theoretical estimates for the E1M1 transition rate of this ${}^{3}{P}_{0}\ \to {\;}^{1}{S}_{0}$ line have been provided by Schmieder [18] for beryllium-like ions with Z = 12 to 20 as well as by Laughlin [19] who made use of a Z-expansion method in order to derive the scaling rule $\ {A}_{\;{\rm{E}}1{\rm{M}}1}^{({\rm{nr}})}\ \approx 5\times {10}^{-18}\ {Z}^{9}\ {s}^{-1},$ and which predicts lifetimes as long as 2 × 10⁸ s, 51s, and 0.4 s for beryllium-like Ne⁶⁺, Xe⁵⁰⁺, and U⁸⁸⁺ ions, respectively. From these computations, Laughlin concluded that the E1M1 transition rates are simply too small in order to become observable in experiments [19]. Only recently, an indirect observation of the lifetime of the $2s2p{\ }^{3}{P}_{0}$ level has been considered in [20] by analyzing the dielectronic recombination (DR) data of zero nuclear-spin beryllium-like ¹³⁶Xe⁵⁰⁺ ions, and a more direct measurement of this lifetime has meanwhile been suggested at the GSI storage ring in Darmstadt [21]. Obviously, such lifetime measurements are of great interest to better understand the electron–photon coupling beyond the well-known dipole approximation.

Already from the $2s\to 1s$ E1E1 transitions in helium-like ions, it is known however that two-photon transition rates may depend quite sensitively on the treatment of relativistic and correlation effects as well as the multipole structure of the radiation field. In this work, we therefore re-explore the $2s2p{\ }^{3}{P}_{0}\to 2{s}^{2}{\ }^{1}{S}_{0}$ E1M1 transition rates for beryllium-like ions with zero nuclear spin within the framework of relativistic second-order perturbation theory. Both a series of multiconfiguration and quantum-electrodynamic computations have been carried out independently in order to explore how the correlated and relativistic motion of the electrons in the initial, intermediate, and final states affect the two-photon rates and lifetimes. From these computations, it is found that the lifetime of the metastable $2s2p{\ }^{3}{P}_{0}$ level is larger by about 2–3 orders of magnitude for all medium and heavy ions along the beryllium isoelectronic sequence than estimated previously. Apart from the relativistic contraction of the wave functions and the proper excitation energies to the levels nearby, especially the electronic correlations in the $2{s}^{2}{\ }^{1}{S}_{0}$ ground state has been found relevant for predicting reasonably accurate lifetimes.

For isotopes with zero nuclear spin, the metastable $2s2p{\ }^{3}{P}_{0}$ level cannot decay by any single-photon transition, and the lowest-order decay channel is the strongly suppressed E1M1 two-photon process into the $2{s}^{2}{\ }^{1}{S}_{0}$ ground state, cf figure 1. The lifetime of this level is expected to be more than 12 orders of magnitude larger than for the neighboured ${}^{\mathrm{1,3}}{P}_{1}$ levels and still more than 10 orders of magnitude longer than for the ${}^{3}{P}_{2},$ which predominantly decays via M2 transitions. For such two-photon transitions, second-order perturbation theory is required in order to describe the coupling of the radiation field, while the major electron–electron interaction contributions are usually treated non-perturbatively by some proper wave function expansion of the initial, intermediate, and final states. Indeed, the selection rules for the multi-photon transitions are derived quite easily from the standard single-photon selection rules with regard to differences in their total angular momenta ΔJ and the parity P, and by taking into account the possible multipole transitions to the (virtual) intermediate states within the spectrum of the atom or ion.

Zoom In Zoom Out Reset image size

Because a good number of second-order perturbation calculations have been performed recently to study the two-photon decay of helium- [2, 3, 10, 23] and beryllium-like ions [24], we here restrict ourselves to a short compilation of the basic formulas as needed for the discussion next. In a relativistic, jj–coupled representation of the atomic bound states involved, the second-order transition amplitude for the emission of two photons with wave vectors ${{\boldsymbol{k}}}_{i}$ (i = 1, 2) and polarization vectors ${{\boldsymbol{u}}}_{{\lambda }_{i}}$ (λ_i = ±1 ) is given by [10, 24]

$$\begin{eqnarray}&&{M}_{{fi}}({M}_{f},{M}_{i},{\lambda }_{1},{\lambda }_{2})\\ &&\quad =\displaystyle \sum _{{\alpha }_{\nu }{J}_{\nu }{M}_{\nu }}\displaystyle \frac{\left\langle {\alpha }_{f}{J}_{f}{M}_{f}\right|{\hat{{\mathcal{R}}}}^{\dagger }({{\boldsymbol{k}}}_{1},{{\boldsymbol{u}}}_{{\lambda }_{1}})\left|{\alpha }_{\nu }{J}_{\nu }{M}_{\nu }\right\rangle \left\langle {\alpha }_{\nu }{J}_{\nu }{M}_{\nu }\right|{\hat{{\mathcal{R}}}}^{\dagger }({{\boldsymbol{k}}}_{2},{{\boldsymbol{u}}}_{{\lambda }_{2}})\left|{\alpha }_{i}{J}_{i}{M}_{i}\right\rangle }{{E}_{\nu }-{E}_{i}+{\omega }_{2}}\\ &&\qquad +\displaystyle \sum _{{\alpha }_{\nu }{J}_{\nu }{M}_{\nu }}\displaystyle \frac{\left\langle {\alpha }_{f}{J}_{f}{M}_{f}\right|{\hat{{\mathcal{R}}}}^{\dagger }({{\boldsymbol{k}}}_{2},{{\boldsymbol{u}}}_{{\lambda }_{2}})\left|{\alpha }_{\nu }{J}_{\nu }{M}_{\nu }\right\rangle \left\langle {\alpha }_{\nu }{J}_{\nu }{M}_{\nu }\right|{\hat{{\mathcal{R}}}}^{\dagger }({{\boldsymbol{k}}}_{1},{{\boldsymbol{u}}}_{{\lambda }_{1}})\left|{\alpha }_{i}{J}_{i}{M}_{i}\right\rangle }{{E}_{\nu }-{E}_{i}+{\omega }_{1}},\end{eqnarray} \tag{ 1 }$$

where $\left|{\alpha }_{i}{J}_{i}{M}_{i}\right\rangle$ and $\left|{\alpha }_{f}{J}_{f}{M}_{f}\right\rangle$ refer to the initial and final atomic states with well-defined total angular momenta J_{i, f} and magnetic projections M_{i, f}, respectively, and where α_{i, f} denote all additional quantum numbers that are necessary for a unique specification of these states. The transition operator $\hat{{\mathcal{R}}}$ describes the interaction of the electrons with the (spontaneous) field fluctuations and can be written in velocity (Coulomb) gauge as a sum of the one-particle multipole operators:

$$\begin{eqnarray}&&\hat{{\mathcal{R}}}({\boldsymbol{k}},{{\boldsymbol{u}}}_{\lambda })=\displaystyle \sum _{m}{{\boldsymbol{\alpha }}}_{m}\;{{\boldsymbol{u}}}_{\lambda }\;{{\rm{e}}}^{{\rm{i}}{\boldsymbol{k}}\cdot {{\boldsymbol{r}}}_{m}},\end{eqnarray} \tag{ 2 }$$

where ${{\boldsymbol{\alpha }}}_{m}=\left({\alpha }_{x,m},{\alpha }_{y,m},{\alpha }_{z,m}\right)$ denotes the vector of the Dirac matrices for the mth particle ⁵ .

The well-known multipole decomposition of the electron–photon interaction operator (2) also enables one to simplify the second-order amplitude (1) and to re-write it in terms of the standard single-photon amplitudes [25–27] by just keeping a summation over all (one-electron) continua of the atom. In this simplified form, each photon is identified as an irreducible component of the radiation field which, apart from its frequency, has also a well-defined multipolarity L and parity P. From the reduced two-photon amplitudes, one then obtains the total rate by integrating the (energy-) differential rate over half of the transition energy, $\ {\displaystyle \int }_{0}^{({E}_{i}-{E}_{f})/2}{\rm{d}}{\omega }_{1}\ \frac{{\rm{d}}w}{{\rm{d}}{\omega }_{1}}\$ for the first photon, while the energy of the second photon is fixed of course due to energy conservation.

Expression (1) of the transition amplitude is quite standard for second-order perturbation theory and appears similarly also in studying two-photon excitation and ionization processes [24], or even the Rayleigh scattering of high-energetic photons at heavy target materials [28–30]. The main differences in calculating the various—energy-differential and total—two-photon transition rates and cross sections typically arise from the different representation of the atomic bound states as well as the particular procedure in dealing with the integration over the complete spectrum of intermediate states. Most generally, this integration includes a summation over the discrete part of the spectrum as well as an integration over the positive- and negative-energy continua. In a radial-angular representation of the (many-electron) atomic states one often distinguishes different continua, owing to their overall symmetry J_ν and P_ν with regard to a rotation and inversion of coordinates. In the amplitudes (1), this symmetry of the continua is encoded into the symmetries of the intermediate states $\left|{\alpha }_{\nu }{J}_{\nu }\right\rangle$ and requires them to be consistent with the particular multipoles of the radiation field as well as the representation of the (correlated) initial and final states of the given transition. In the present work, we independently applied two different methods to evaluate these amplitudes: (i) the multiconfiguration Dirac–Fock (MCDF) method, in which all atomic states of interests are built from a finite set of jj-coupled configuration state functions (CSF) and (ii) quantum-electrodynamical calculations, based on a perturbative treatment of the interelectronic interaction. In the following, we briefly explain these two different approaches and how they can be simplified in order to keep the computations feasible.

2.1. Use of relativistic wave function expansions

In the MCDF method, to summarize the first approach, a representation of all atomic states involved in expression (1) are generated by using linear combinations of CSF of the given symmetry [26]

$$\begin{eqnarray}&&{\psi }_{\alpha }({PJ})=\displaystyle \sum _{r=1}^{{n}_{c}}\;{c}_{r}(\alpha )\;\left|{\gamma }_{r}{PJ}\right\rangle ,\end{eqnarray} \tag{ 3 }$$

where n_c refers to the number of CSF and { c_r(α) } to the representation of the atomic state(s) in this many-electron basis. Like in standard computations, the CSF are constructed as antisymmetrized products of a common set of orthonormal orbitals and are optimized on the basis of the Dirac–Coulomb Hamiltonian. Relativistic effects due to the Breit interaction, i.e., the magnetic and retardation contributions to the electron–electron interaction, were then added to the representation $\{{c}_{r}(\alpha )\}$ by diagonalizing the Dirac–Coulomb–Breit Hamiltonian matrix [31, 32]. To describe excitation and decay processes in multiple and highly-charged ions the MCDF method has been found a very versatile tool, especially if inner-shell electrons or different open shells are involved in the computations [33, 34].

To generate the initial $2s2p{\ }^{3}{P}_{0}$ and final $2{s}^{2}{\ }^{1}{S}_{0}$ atomic states as well as the relevant intermediate states of the spectrum in equation (1), a series of computations has been carried out based on the three $1{s}^{2}(2{s}^{2}+2s2p+2{p}^{2})$ reference configurations. Especially for the $2{s}^{2}{\ }^{1}{S}_{0}$ ground state of beryllium-like ions, the double excitations $2{s}^{2}\;\to 2{p}^{2}$ and $2{s}^{2}\;\to 3{s}^{2}$ are known to be quite important and, for neutral beryllium, they alone give rise to about 65% of the overall correlation energy for the $2{s}^{2}{\ }^{1}{S}_{0}$ ground level [35]. Using these reference configurations, the wave function expansions have then been enlarged stepwise in order to incorporate all $1{s}^{2}(2{s}^{2}+2{p}^{2}+2{sns}+2{snp}+2{snd}){\ }^{\mathrm{1,3}}{L}_{J}$ levels with ${J}^{P}=\ {0}^{+}$ and 1⁻as well as n ≤ 30, and by including also single excitations of Brillouin's type [36, 37]. This results in a total of 290 intermediate states with energies partially well above of the single and double ionization limit. Because of the discretization of the radial grid for the representation of the CSF, this procedure effectively incorporates a summation over the continuum since single-electron excitations with $n\;\gtrsim 8$ usually belong already to the continuum of the corresponding lithium-like and, for higher n, also to the helium-like ions. A great advantage of the MCDF method is that different approximations with regard to the electron–electron correlations as well as the summation over the continuum can be explored rather readily by choosing sets of CSF due to different classes of excitations [38].The major computational models that were used in the present calculations will be explained next in section 3 together with the ³P₀ − ¹S₀ E1M1 transition rates.

Apart from the Breit interaction in the Hamiltonian matrix, we also included the vacuum polarization into the Hamiltonian but no self-energy corrections that are more difficult to handle, especially for highly excited states within the continuum. For the low-lying levels, however, all major QED corrections are incorporated implicitly by applying accurate theoretical excitation energies [14, 22, 39] in the summation over the intermediate states, though these corrections are not included into the wave function representation itself. This clearly improves the agreement between the different approximations. Especially for the transition energies to the two lowest levels, the uncertainties were estimated in these references to about $6\times {10}^{-3}$ eV for the ³P levels and $6\times {10}^{-2}$ eV for the ¹P level [22]. From the comparison of these results we also learned about the uncertainties that arise from the different approximations.

2.2. Quantum-electrodynamical treatment

In the QED treatment, we have accounted for the electron–electron correlation within the framework of perturbation theory. In the zeroth-order approximation, we here solve the Dirac equation with a local screening potential, which partially incorporates already the interelectronic interaction. Indeed, the inclusion of a screening potential into the unperturbed Hamiltonian is known as the extended Furry picture, a picture that enables one to remove the quasi-degeneracy of the levels in the Coulomb potential and which improves the low-lying excitation energies already in zeroth-order approximation. The remaining interelectronic interaction is then taken into account via the QED perturbation expansion following the description of [23]. In the present calculations, we have rigorously taken into account all the first-order QED diagrams as depicted in figure 2. The formal expressions for these diagrams in the case of a four-electron ion have been derived in a same way as it was done for two-electron ions in [23] previously. We note, however, that the E1M1 transitions rates appear to be quite sensitive to the treatment of the intermediate $1{s}^{2}2s2{p}_{1/2}\ J=1$ level (which, in first order in the electron–electron interaction, is just represented by a single determinant). Owing to this sensitivity, we have extended our approach to partially account for the contributions with this intermediate state not only in the first-order but in second and higher orders with regard to the electron–electron interaction. For this intermediate state, in particular, we therefore performed a complete resummation of the ladder diagrams.

Zoom In Zoom Out Reset image size

The rigorous QED approach employed in this work enabled us to perform the calculations without an α Z-expansion, i.e., beyond the (so-called) Breit approximation. This approach accounts for the frequency-dependence in the exact photon propagator, and for the interaction of bound electrons also with the Dirac continuum, i.e. the summation runs over the complete Dirac spectrum of the positive and negative energy states. As first shown in [40], the contribution from the negative-continuum energy states can be of a great importance especially for the cases of M1 transitions. The negative-continuum effects were investigated also for the transitions in beryllium-like ions in [41, 42], and for hydrogen-like ions, in [43, 44]. In the present QED approach, we also sum over the negative-continuum energy states and, hence, evaluate this contribution explicitly, similar as done for the helium-like ions in [23, 45]. In some further detail, this summation over the spectrum has been performed by employing the dual-kinetic-balance finite basis set method [46] with basis functions constructed from B-splines [47].

As outlined previously, the major difficulty in calculating the two-photon transition amplitude (1) and rates arises from the summation over the intermediate states and the extent to which the electron–electron correlation is finally taken into account in the representation of the atomic bound states. For the $1{s}^{2}2{s}^{2}{\ }^{1}{S}_{0}$ ground state of beryllium-like ions, for example, sizeable correlation contributions are added by virtual double excitations of the $2{s}^{2}$ electrons into the 2p and $3s$ shells, and which can be omitted only for high-Z ions. Other single and double excitations also affect the $1{s}^{2}2s2p{\ }^{3}{P}_{0}$ level and, similarly, also the representation of the intermediate states. For these reasons, all atomic states in the MCDF computations were based on the $1{s}^{2}(2{s}^{2}+2s2p+2{p}^{2})$ reference configurations, together with possible single and double excitations of the 2>̃ s and 2p electrons. Moreover, in order to generate a proper one-particle spectrum that covers both the bound and continuum states of the individual electrons, a x_α local-density potential was used [48, 49], and where α was chosen to reproduce the binding energies of the electron in the low-lying $1{s}^{2}2l2l^{\prime}$ levels. To further understand the effects of different correlation contributions to the two-photon transition amplitude, a series of systematically enlarged wave function expansions (3) was utilized to evaluate the E1M1 rates as function of the nuclear charge Z. Apart from the independent-particle model, a number of multi-configuration expansions were analyzed especially for their influence of how the summation over the $2s2l{\ }^{\mathrm{1,3}}{L}_{1}$ states with $n\;\geqslant \;3$ as well as the 2p² correlation contributions to the ¹S₀ ground state eventually affect the E1M1 amplitude. While, typically, deviations of up to a factor 2 occured for different multi-configuration expansions (3), the results tend to converge with increasing number of states in the representation of the one-particle spectra. The remaining deviations are also quite moderate with regard to the overall relativistic effects. Here, we shall not discuss all these computations in great detail but just display our best results, i.e., those from the largest expansions (3), and compare them with the independent QED computations and previous (non relativistic) estimates; cf figure 3 and table 1.

Zoom In Zoom Out Reset image size

Table 1.  The lifetimes of the $2s2p\ {}^{3}{P}_{0}$ state and rates for the $2s2p\ {}^{3}{P}_{0}\to 2{s}^{2}\ {}^{1}{S}_{0}$ E1M1 decay of beryllium-like ions. Results of the QED computations are compared with the nonrelativistic prediction equation (5) previously obtained by Laughlin [19]. In the second column we also present the corresponding transition energies from [14] that were employed in present calculations. Numbers in square brackets denote powers of ten.

		Lifetime (s)		Decay rate (s−1)
	Transition
Z	energy (eV)	${\tau }_{{\rm{E}}1{\rm{M}}1}^{(\mathrm{QED})}$	${\tau }_{{\rm{E}}1{\rm{M}}1}^{(\mathrm{nr})}$	${A}_{{\rm{E}}1{\rm{M}}1}^{(\mathrm{QED})}$	${A}_{{\rm{E}}1{\rm{M}}1}^{(\mathrm{nr})}$
10	13.794	1.2[9]	2.0[8]	8.5[-10]	5.0[-9]
18	28.352	4.2[6]	1.0[6]	2.4[-7]	9.9[-7]
26	43.169	2.9[5]	3.7[4]	3.4[-6]	2.7[-5]
40	70.946	2.3[4]	7.6[2]	4.3[-5]	1.3[-3]
54	104.475	4.0[3]	5.1[1]	2.5[-4]	1.9[-2]
79	193.670	2.8[2]	1.7[0]	3.6[-3]	5.9[-1]
92	257.564	9.1[1]	4.2[-1]	1.1[-2]	2.4[0]

In the QED approach, similarly, different screening potentials were employed to understand the interplay of relativity and correlations in predicting accurate transition rates. These potentials include the core–Hartree, Kohn–Sham, Perdew–Zunger, and local Dirac–Fock potentials. All these screening potentials have been utilized quite frequently in recent QED calculations and need not to be described here in detail. In [50, 51], for example, these potentials were applied to calculate the binding and ionization energies of beryllium-like ions. Moreover, to make use of perturbation theory in dealing with electron–electron correlations, the first-order corrections to the transition energies and amplitudes were derived. For a given order in the electron–electron interaction the corrections to the energies and rates are gauge invariant. This invariance provides an excellent tool to check for the consistency of a formally equivalent expression and for the numerical implementation of all diagrams. However, if one applies only first-order perturbation theory for the inter–electronic interaction, the two-photon transition energy typically differs quite sizeably from the experiment. This applies to both the low-Z ions because of missing correlation contributions as well as to high-Z ions, for which the radiative corrections become important. For this reason, we employed the total transition energies $({E}_{i}-{E}_{f})$ from [14] here. Again, we have also investigated here the role of the negative continuum and found that its contribution is less than 8% within the velocity gauge and less than 1% in the length gauge for any of the screening potentials employed here. In our final QED computations, as displayed in figure 3, the local Dirac–Fock potential and the length gauge were used to calculate the two-photon transition rates. By comparing the results for the four screening potentials from previously, an uncertainty of 10–20% is estimated for the two-photon transition rates apart, perhaps, from the low-Z region for which the perturbation theory converges only slowly and where we assign an uncertainty of about 50%.

Figure 3 displays the E1M1 two-photon transition rates for the $2s2p{\ }^{3}{P}_{0}\to 2{s}^{2}{\ }^{1}{S}_{0}$ transition of zero nuclear-spin beryllium-like ions as a function of the nuclear charge Z. Results are shown from our best MCDF and QED computations and are compared with previous nonrelativistic estimates that are available in the literature. Most other computational models that were analyzed differ by less or about a factor 2 and were taken to estimate the accuracy of the calculations. A proper treatment of the electron–electron interaction, in particular, leads to some clear reduction of the transition rates, and this applies to both the MCDF and QED computations. In figure 3, our fully relativistic calculations are compared also with the nonrelativistic estimates by Schmieder ([18], red open diamonds) and Laughlin [19]; cf table 1. While Schmieder performed nonrelativistic computations for six selected ions with Z = 12 to 20 and restricted the summation over the intermediate states to just the two dominant $2s2p{\ }^{3}{P}_{1}$ and $2s2p{\ }^{1}{P}_{1}$ levels, Laughlin [19] applied a Z-expansion and also presented his results in terms of a closed formula:

$$\begin{eqnarray}&&{A}_{{\rm{E}}1{\rm{M}}1}^{(\mathrm{nr})}=4.8\times {10}^{-12}\cdot {Z}^{4}{({E}_{{\gamma }_{1}}+{E}_{{\gamma }_{2}})}^{5}\ {{\rm{s}}}^{-1},\end{eqnarray} \tag{ 4 }$$

where $E={E}_{{\gamma }_{1}}+{E}_{{\gamma }_{2}}$ denotes the ${}^{3}{P}_{0}{-}^{1}{S}_{0}$ transition energy (in atomic units) as shared by the two photons. The non relativistic estimate ${E}_{{\gamma }_{1}}+{E}_{{\gamma }_{2}}=0.06487\;Z$ for this transition energy then leads to the simple scaling

$$\begin{eqnarray}&&{A}_{{\rm{E}}1{\rm{M}}1}^{(\mathrm{nr})}\approx 5\times {10}^{-18}\;{Z}^{9}\;{{\rm{s}}}^{-1}\end{eqnarray} \tag{ 5 }$$

as displayed by the green solid circles in figure 3. If we use instead the correct two-photon energy in equation (4), the black triangles are obtained, showing some moderate though not negligible reduction of the two-photon transition rate for medium and heavy ions; see [20]. Schmieder [18] also estimated the rate for a 3E1 three-photon decay that is suppresed by at least a factor α, the fine-structure constant, as well as the small ³P₀ − ¹S₀ transition energy. This has been confirmed by our own estimates for this three-photon decay with rates of about ${10}^{-20}\ {{\rm{s}}}^{-1}$ and $5\cdot {10}^{-17}\ {{\rm{s}}}^{-1}$ for beryllium-like argon and uranium, respectively. When compared with the non relativistic estimates for the E1M1 two-photon rates, the relativistic transition rates are clearly lowered for all medium and heavy elements and deviate from previous computations by more than three orders of magnitude for the heaviest beryllium-like ions. For more accurate predictions, our QED computations indicate also that the radiative corrections to the two-photon transition amplitudes need to be taken into accout, a task that has never been considered before in the literature.

All calculations were made for the transition amplitudes (1) and the corresponding E1M1 rates as summarized in figure 3. Obviously, the major decrease of these rates arises from the relativistic contraction of the electron density as well as the treatment of the electron–electron interaction. No attempt has yet been made however, to include the radiative corrections, and especially the self-energy diagrams, into the evaluation of the two-photon transition rates. Of course, the strong reduction of the two-photon transition rate is associated also with a much longer lifetime of the $1{s}^{2}2s2p{\ }^{3}{P}_{0}$ level since no other decay channel is simply possible for isolated ions in this lowest-excited level along the beryllium isoelectronic sequence. For zero nuclear-spin isotopes, this reduction in the transition rates gives rise to lifetimes as long as ${\tau }_{{\rm{E}}1{\rm{M}}1}^{(\mathrm{QED})}=\ 4.2\cdot {10}^{6}$ s, $4.0\cdot {10}^{3}$ s, and 91 s for Ar${}^{14+},$ Xe${}^{50+},$ and ${{\rm{U}}}^{88+}$ ions, respectively; see table 1.⁶ Therefore, ions with a nuclear charge larger than Xe⁵⁰⁺ are likely more preferable for performing lifetime measurements as proposed for the GSI storage ring [21].

For such measurements, indeed, lifetimes longer than about a second are required in order to have time to prepare the ions in the $1{s}^{2}2s2p{\ }^{3}{P}_{0}$ level, while they should not exceed the ion-beam storage due to vacuum conditions and intra-beam scattering processes [20]. If these two conditions are fulfilled, the strength of the resonances as a function of storage time may help measure directly the E1M1 two-photon transition rate. In practice, however, external electric and magnetic fields might also be important and may induce single-photon transition, which would shorten the lifetime of the zero nuclear-spin beryllium-like ions in the $1{s}^{2}2s2p{\ }^{3}{P}_{0}$ level. Such magnetically induced E1 transition, sometimes refered to as MIT, have been explored recently by Grumer et al [52] and were found, for typical storage ring environments, comparable in order as obtained for the E1M1 two-photon rates. In addition, Maul et al [53] investigated the effects of the so-called Stark quenching for the beryllium-like ions due to external electric fields.

In summary, the E1M1 transition rate of the $2s2p{\ }^{3}{P}_{0}\to 2{s}^{2}{\ }^{1}{S}_{0}$ line in zero nuclear-spin beryllium-like ions has been calculated within the framework of relativistic second-order perturbation theory. Both multiconfiguration and quantum-electrodynamic computations were independently performed in order to include and test for all major contributions that affect this rate, such as the relativistically contracted wave functions and electron–electron correlations in the representation of the initial, intermediate, and final states. From the comparison of these two methods, which agree reasonably well for all ions along the beryllium isoelectronic sequence, the lifetime of the metastable $2s2p{\ }^{3}{P}_{0}$ level is found to be larger by about 2–3 orders of magnitude larger than predicted previously. This makes the ³P₀ level of zero nuclear-spin beryllium-like ions to one of the longest living (low-lying) electronic excitations of a tightly bound system with potential applications for atomic clocks [54] or for studying correlation effects in high-Z ions [55].

AV acknowledges the support of the DFG under the project No. VO 1707/1-2.