Exploring quasiparticles in high-T_c cuprates through photoemission, tunneling, and x-ray scattering experiments

Understanding the elementary excitations of superconducting cuprates is one of the central problems in the field of high-T_c superconductivity. It is widely accepted that the quasiparticle spectrum involves two distinct energy scales: the superconducting gap and the 'pseudogap' (see for example [1, 2] and references therein). However, the physical origin of the pseudogap is still debated. One common interpretation relates the pseudogap to a distinct long-range order that competes with superconductivity. Supporting evidence for this order was provided by periodic modulations in scanning tunneling microscope (STM) maps [3–8], pronounced peaks in x-ray scattering [9–13], and quadrupole broadening in nuclear-magnetic resonances (NMR) [14]. The simplest interpretation of both experiments is the presence of an incommensurate charge–density–wave (CDW) order coexisting with superconductivity. This competition can be described in terms of first-principles two-gap theories (see for example [15, 16]). However, two gap models do not provide an adequate description of all experimental observations. Motivated by angle-resolved photoemission spectroscopy (ARPES)³ and electrical conductivity measurements [17], in this paper we explore a scenario in which the second energy scale characterizing the pseudogap phase is the finite inelastic relaxation rate of antinodal quasiparitcles. We develop a simple phenomenological model that accurately describes the experimental observations and, in particular, accounts for the wavevector and correlation length of the spatial modulations .

Our interpretation of the experimental results relies on a weak-coupling analysis of the interplay between finite quasiparticle lifetime and disorder in d-wave superconductors. Even in the absence of true CDW order, Friedel oscillations around a single impurity can give rise to short-range incommensurate checkerboard patterns. For materials with a long quasiparticle lifetime, these oscillations are well described by the 'octet model' [18] and appear as dispersive peaks in the STM spectra [19]. In contrast, when the quasiparticle lifetime is short, we find that the STM spectra exhibit non-dispersive peaks close to the antinodal scattering wavevectors. The predicted signal for both STM and resonant elastic x-ray scattering (REXS) agrees quantitatively with recent experiments on (Pb_x,Bi_2-x)₂(La_y,Sr_2-y)CuO_6+δ (Pb-Bi2201) [12, 20, 21], Bi₂Sr₂CaCu₂O_8+δ (Bi2212) [13, 22–26], and YBa₂Cu₃O_7-x (Y123) [10].

The present analysis does not rule out the existence of competing orders in cuprates. In particular, all cuprates become antiferromagnetic when approaching zero doping, in the Mott insulating phase. Similarly, at $1/8$ filling ${\rm L}{{{\rm a}}_{2-x}}{\rm B}{{{\rm a}}_{x}}{\rm Cu}{{{\rm O}}_{4}}$ [9] displays sharp diffraction peaks, accompanied by a suppression of the superconducting critical temperature T_c. An analogous effect was recently observed by NMR [27] and quantum oscillations [28] at high magnetic fields, as well. These phenomena indicate the onset of a true long-range order and require a separate analysis [29] ⁴ .

The starting point of our analysis of fermionic quasiparticles in cuprates is the retarded Green's function $G(k,\omega )$. In the absence of disorder, and using the Nambu notation (see [32] for an introduction), it satisfies

$$\begin{eqnarray}{{G}^{-1}}(k,\omega )=\left( \begin{array}{ccccccccccccccc} \omega -{{\epsilon }_{k}}+\mu +{\rm i}{{\Gamma }_{k}} & {{\Delta }_{k}} \\ {{\Delta }_{-k}} & \omega +{{\epsilon }_{-k}}-\mu +{\rm i}{{\Gamma }_{-k}} \\ \end{array} \right).\end{eqnarray} \tag{ 1 }$$

The four ingredients of equation (1) are: (i) a phenomenological band structure ${{\epsilon }_{k}}$, obtained from ARPES measurements (we use the single-band model of [33] for both Bi2212 and Pb-Bi2201, and the two-band model of [34] for Y123); (ii) a doping-dependent shift of the chemical potential μ (measured with respect to the aforementioned models); (iii) a d-wave pairing gap ${{\Delta }_{k}}={{\Delta }_{0}}/2\left( {\rm cos} ({{k}_{x}})-{\rm cos} ({{k}_{y}}) \right)$; (iv) an inverse quasiparticle lifetime ${{\Gamma }_{k}}$, describing the inelastic scattering of quasiparticles. Microscopically, ${{\Gamma }_{k}}$ is due to electron–electron interactions, but it can also be conveniently described as the inelastic scattering of quasiparticles on dynamic charge and spin fluctuations [35]. At zero temperature, ${{\Gamma }_{k}}$ vanishes for quasiparticles with ${{\epsilon }_{k}}=\mu$, but it is generically finite and positive elsewhere. Because, as we will show, STM and REXS signals are dominated by the scattering of quasiparticles with specific momentum (antinodal quasiparticles), these experiments are well described by the simplifying assumption of a constant ${{\Gamma }_{k}}\equiv \Gamma$ [36] (see also SI-3, where we consider the effects of an anisotropic scattering rate).

STM probes the differential conductance $g(r,V)\equiv {\rm d}I(r,V)/{\rm d}V={\rm Im}\left[ \mathcal{G}(r,V) \right]$. In the presence of weak time-independent scatterers its Fourier transform is given by [18, 37–41], $\mathcal{G}(k,k^{\prime} ,V)=G(k,V){{\delta }_{k,k^{\prime} }}$ $+\;G(k,V)T(k,k^{\prime} )G(k^{\prime} ,V)$, where $T(k,k^{\prime} )$ describes the scattering of quasiparticles from momentum k to momentum $k^{\prime}$. In the case of long-range-ordered waves the elements of $T(k,k^{\prime} )$ are sharply peaked around the ordering wavevector $q=k-k^{\prime}$. In contrast, for local impurities the scattering amplitude does not depend on the momentum difference and, for $q\ne 0$, we have (see also SI-2)

$$\begin{eqnarray}&&g(q,V)={{{\rm e}}^{{\rm i}q{{r}_{0}}}}\mathop{\sum }\limits_{k-k^{\prime} =q}{\rm Im}\left[ G(k,V)\left( {{T}_{k}}+{{T}_{k^{\prime} }} \right)G(k^{\prime} ,V) \right].\end{eqnarray} \tag{ 2 }$$

Here r₀ is the position of the impurity and T_k is a k-dependent 2 × 2 matrix describing the scattering process. We stress that equation (2) relies on the Born approximation to describe the scattering of independent quasiparticles (with a finite lifetime) from local impurities: it does not require an enhancement due to electron–electron interactions, nor imply a finite stability threshold.

By comparing the intensity of the predicted signal, equation (2), with the experimental observations at an arbitrary wavevector we are able to uniquely determine the pairing gap ${{\Delta }_{0}}$, the quasiparticle lifetime Γ, and chemical potential μ throughout the whole superconducting dome (see Methods section and table 1). We find that both ${{\Delta }_{0}}$ and Γ increase with underdoping, i.e. as approaching the antiferromagnetic insulating phase, in agreement with previous theoretical calculations (FLEX approximation [42] and functional RG [43]) and experimental observations (magneto-resistance of ${\rm T}{{{\rm l}}_{2}}{\rm B}{{{\rm a}}_{2}}{\rm Cu}{{{\rm O}}_{6+\delta }}$ [44] and STM of Bi2212 [23]). By studying the symmetry of the voltage with respect to $V\to -V$ we can further identify the nature of the dominant source of scattering. As explained in the methods section, we find that (at low temperatures) the dominant source of disorder is due to local modulations of the pairing gap.

Table 1.  Phenomenological parameters found by comparing theory and experiment at $\vec{q}=(0.25,0)\times 2\pi$ for four samples of Pb-Bi2201. The name of the sample indicates whether the sample is overdoped (OD), optimally doped (OPT), or underdoped (UD) and its critical temperature. The chemical potential is measured with respect to the band structure of [33]. The concentration of holes (p) is obtained from the Luttinger count (i.e. counting the number of states with ${{\epsilon }_{k}}\lt \mu$) and found in good agreement with ARPES measurements in the normal phase [63]. All energies are given in meV and the precision of each entry is of about 10%.

	${{\Delta }_{0}}$	Γ	μ (p)
OD15K	8	6	−30 (p = 0.33)
OPT35K	18	7	−15 (p = 0.24)
UD32K	20	8	−5 (p = 0.20)
UD25K	22	10	5 (p = 0.16)

Having extracted all the model parameters from the voltage dependence at an single wavevector, we can now compute the STM signal at all wavevectors without any additional fitting parameter. Figure 1(a) shows our theoretical predictions for wavevectors aligned along the Cu-O axis, $\vec{q}=(q,0)\times 2\pi$. Our calculations clearly indicate a non-dispersive peak at wavevector $q\approx 0.2\times 2\pi$ for voltages $5\;{\rm meV}\lesssim V\lesssim 20\;{\rm meV}$, which was observed in experiments (figures 1(a)–(b)). Figures 1(d)–(g) demonstrate that our model quantitatively predicts the wavelength and the width of the incommensurate peaks at all dopings. Remarkably, our model includes only scattering from local impurities, without any long-range density or pairing waves. The peaks observed in the STM experiments result from an enhanced scattering of antinodal quasiparticles (see also SI-3). Because the quasiparticles have a finite lifetime, their energy does not need to be exactly conserved during a scattering event. The scattering at wavevectors connecting antinodal quasiparticles is then strongly enhanced at all voltages, giving rise to broad non-dispersive peaks in the STM signal.

Zoom In Zoom Out Reset image size

To highlight the effects of a finite quasiparticle lifetime, we repeat the above calculations for a smaller value of Γ (figure 1(c)). The predicted signal displays dispersive features for $V\lt {{\Delta }_{0}}$ and sharp non-dispersive features for $V\gt {{\Delta }_{0}}$, in agreement with low-temperature STM measurements of Bi2212 (see [25] for a review). Our theoretical calculations predict the appearance of an intermediate regime in which both types of peaks disappear and are substituted by broad non-dispersive peaks. As shown in SI-4, the upper and lower boundaries of this intermediate regime are proportional to ${{\Delta }_{0}}-\Gamma$ and ${{\Delta }_{0}}+\Gamma$ respectively. With increasing underdoping, both ${{\Delta }_{0}}$ and Γ become larger [23] and the two boundaries move apart: the lower boundary is approximately constant, while the upper one shifts to higher energies. (See also SI-5 for the appearance of two energy scales in the real-space spectra.) Accordingly, at higher temperatures [6] and at lower doping values [13], the non-dispersive peaks were observed to extend down to zero voltage. An analogous interplay between dispersive and non-dispersive peaks was observed in the autocorrelation analysis of ARPES data [45, 46]. We propose that Γ may play the role of the second energy scale detected in the pseudogap phase, approached with increasing underdoping and/or temperature.

Our theoretical approach accounts for all the key features of the non-dispersive peaks. In particular, our calculations show that these features are stronger at positive voltages than at negative one: see figures 1(a)–(b) and 2. At low voltages $V\ll \Delta$, the symmetry of the signal with respect to $V\to -V$ is determined by the nature of the impurities: modulations of the chemical potential lead to a signal that is mainly anti-symmetric, while modulations of the pairing gap lead to a signal that is mainly symmetric. However, the non-dispersive peaks are most prominent at $V\sim \Delta$, where this symmetry does not hold. In particular, in figures 1(b) and 2(a)–(c) we considered only the effects of local perturbations of the pairing gap. The predicted signals at $V\sim \Delta$ and $V\sim -\Delta$ is very different, and non-dispersive peaks are evident only in the former.

Zoom In Zoom Out Reset image size

The non-dispersive peaks were observed to persist to the temperature $T*\gg {{T}_{{\rm c}}}$ [47], marking the transition from the pseudogap phase to the normal phase. In our model the intensity of the non-dispersive peaks is roughly proportional to ${{\Delta }_{0}}$, indicating that a local superconducting gap may be present in the pseudogap phase, even though its long range coherence is already suppressed. As pointed out by Fischer et al [48], this argument is consistent with the observation that the ratio $T*/{{\Delta }_{0}}$ is approximately constant in all cuprates. Experimental evidence for superconducting fluctuations well above T_c also comes from recent μSR data by Mahyari et al [49]. In SI-1 we show that this model is consistent with ARPES measurements as well [50, 51].

Up to this point, we considered the STM signal along a specific momentum cut (parallel to the Cu-O axis) only. In order to reproduce the full two-dimensional $({{q}_{x}},{{q}_{y}})$ dependence, we need to take into account two additional factors. First, local modulations of the gap do not scatter quasiparticles at ${{\vec{q}}_{\pi ,\pi }}=(0.5,0.5)\times 2\pi$ because at this wavevector the integrand of equation (2) is identically zero (due to the d-wave symmetry of the gap, ${{T}_{k}}+{{T}_{k+{{q}_{\pi ,\pi }}}}\sim {{\Delta }_{k}}+{{\Delta }_{k+{{q}_{\pi ,\pi }}}}=0$). In contrast, the experimental signal shows a broad peak around this wavevector. As shown in SI-6, the peak at ${{\vec{q}}_{\pi ,\pi }}$ is due to local modulations of the chemical potential, which coexist with the local modulations of the gap. Along the Cu-O axis, the coherence factors appearing in equation (2) significantly suppress the scattering from modulations of the chemical potential, making the modulations of the gap dominant (see SI-3). To explain the full range of STM results at all wavevectors we need to include both sources of disorder: the experiments are best reproduced by adding modulations of the chemical potential and of the gap with the same amplitude and the same phase . Physically, this implies that the local modulations of μ and ${{\Delta }_{0}}$ have a common origin, probably related to a modified density of carriers around the impurity. This finding is in agreement with [20] who observed a positive correlation between the gap and the wavelength of the incommensurate modulations (which is positively correlated to the chemical potential) and with [52] who found that checkerboard oscillations are mostly pinned by vacancies of apical oxigens, which locally increase the pairing gap and the local electron concentration.⁵

Second, equation (2) refers to a lattice model and predicts a signal that is periodic under $\vec{q}\to \vec{q}+(n,m)\times 2\pi$, where n and m are integers. In contrast, the experimental signal globally decreases as function of q. To explain this effect we need to take into account the overlap function $\psi (r)$, describing the tunneling amplitude of quasiparticles from the tip to the sample. This leads to a modified version of equation (2), which reads [37, 53]:

$$\begin{eqnarray}\begin{array}{rcl} g^{\prime} (q,V) & \equiv & {{{\rm e}}^{{\rm i}q{{r}_{0}}}}{{\sum }_{k}}{\rm Im}\left[ {{\psi }^{*}}(k)G(\omega =V,k)\left( {{T}_{k}}+{{T}_{k+q}} \right) \right. \\ {} & {} & \times \left. G(\omega =V,k+q)\psi (k+q) \right], \\ \end{array}\end{eqnarray} \tag{ 3 }$$

where $\psi (k)=\int {{{\rm d}}^{2}}r{{{\rm e}}^{{\rm i}kr}}\psi (r)$. In our calculations we assume a Gaussian overlap function $\psi (r)={{{\rm e}}^{-{{r}^{2}}/2\delta {{r}^{2}}}}$, or $\psi (k)={{{\rm e}}^{-\delta {{r}^{2}}{{k}^{2}}/2{{a}^{2}}}}$, where a is the lattice constant. The single fitting parameter $\delta r=0.55a$ is phenomenologically determined by the ratio between the Fourier components at small and large wavevectors, and allows us to reproduce the experimental data for all four samples, as shown in figure 3.

Zoom In Zoom Out Reset image size

We now use our understanding of the quasiparticle Green's function to analyze x-ray scattering. Sharp peaks in these experiments are considered a 'smoking-gun' evidence of competing charge order. In particular, we focus here on resonant elastic x-ray scattering (REXS) experiments, in which one electron is transferred to the conduction band from a core hole, characterized by an energy E_h and an inverse lifetime ${{\Gamma }_{h}}$. The simplest description of this process [55, 56] is given by the convolution of $g(q,\omega )$ (which describes the conduction band) with the response function of the core hole, $1/(\omega -{{E}_{h}}+{\rm i}{{\Gamma }_{h}})$:

$$\begin{eqnarray}&&{{I}_{{\rm REXS}}}(q,E)=\left |\int _{0}^{\infty }{\rm d}\omega ^{\prime} {{\frac{g(q,\omega ^{\prime} )}{E-\omega ^{\prime} -{{E}_{h}}+{\rm i}{{\Gamma }_{h}}}}}\right |^{2}.\end{eqnarray} \tag{ 4 }$$

Here the integral from 0 to $+\infty$ indicates that the x-ray beam can only create electron excitations above the Fermi surface (with positive energy).

Before showing the results of our calculations, we now briefly discuss the validity of equation (4). This expression neglects the effects of the core–hole potential, and essentially assumes the core hole and the conduction band to be completely decoupled. The validity of this approximation is still debated in the literature. In particular, Kourties et al [57] found significant effects of the core–hole potential on the predicted experimental signal, while Benjamin et al [56] claims these effects to be negligible. This fundamental debate is however not directly relevant to the present discussion: both Kourtis et al and Benjamin et al considered the energy dependence of the signal, while the present analysis deals with its momentum dependence. Because the core–hole potential has an atomic-size support, its effects are expected to be momentum independent. As a consequence, although equation (4) may not always be sufficient to study the energy dependence, this expression is expected to provide a good approximation for the momentum dependence of REXS experiments.

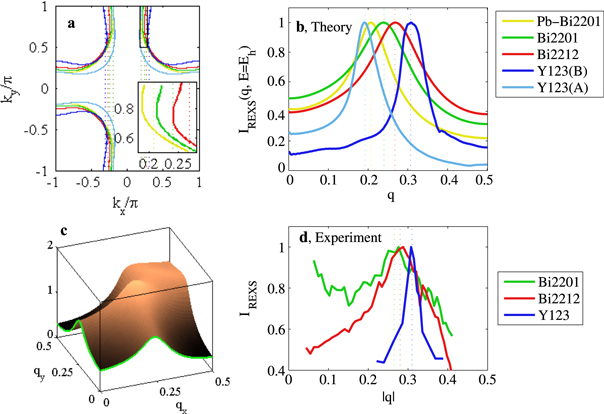
Combining the above calculations of the STM signal $g(q,V)$ with equation (4) at E = 0, we predict the REXS signal in underdoped samples of Pb-Bi2201 (p = 0.16), Bi2201 (p = 0.11), and Bi2212 (p = 0.04) and find a pronounced peak even in the presence of local scatterers only (figure 4(b)). In analogy to the STM signal described above, this peak is due to enhanced coherence factors in the antinodal regions, amplified by the nearly-nested Fermi surface of cuprates. As shown in equation (2), the predicted signal is determined by a weighted sum over all momenta, leading to a maximal intensity at a wavevector that is approximately 10% larger than the antinodal nesting wavevector (see inset of figure 4(a)). The width of the peak (full-width half-maximum $\delta q\approx 0.1$) corresponds to an estimated correlation length of approximately ten atoms, or $\xi \approx 40\;\overset{\circ}{A}$, and is in quantitative agreement with recent measurements [12, 13]. A similar effect was observed in x-ray scattering experiments of Y123 [10, 11]. Our calculations for the bonding (B) band of Y123 exactly reproduce the wavevector $q\approx 0.31$ of the observed signal. The computed width $\delta q\approx 0.07$ is larger than the one extracted from the experiments ($\delta q=0.04\pm 0.01$ corresponding to $\xi =100\pm 20\;\overset{\circ}{A}$ [10, 11]). As shown in SI-7, $\delta q$ strongly depends on the details of the band structure in the antinodal region, which are generically hard to determine from ARPES measurements. In Y123 the precision of these measurements is further impaired by the polarity of the unit cell and the presence of CuO chains [58]. Both effects are absent in Bi2201 and Bi2212, where we expect our predictions to have a better accuracy. In figure 4(c) we predict the two-dimensional dependence of the REXS signal for a sample of Bi2201 with hole doping p = 0.11. We predict that, in addition to the peak at $\vec{q}\approx (0.25,0)\times 2\pi$, a pronounced peak at $\vec{q}\approx (0.25,0.25)\times 2\pi$ should be observed, highlighting the checkerboard nature of Friedel oscillations (see also SI-7). We emphasize that equation (4) has only two free parameters, E_h = 931.5 eV and ${{\Gamma }_{h}}=400$ meV, which can be inferred from the position and width of the x-ray absorption (XAS) peak [10], while all other parameters are fixed from ARPES and/or STM measurements. The REXS signal shown in figures 4(b)–(c) are therefore model-independent consequences of previously-measured quantities.

Zoom In Zoom Out Reset image size

To summarize, in this paper we studied the effect of a finite lifetime of quasiparticles on STM and REXS, and provided a minimal framework to quantitatively describe these experiments. We showed that the inverse lifetime Γ can play the role of a second energy scale detected by different observations. In particular, we demonstrated that the incommensurate checkerboard short-range order observed in superconducting cuprates Pb-Bi2201, Bi2201, Bi2212, and Y123 can be quantitatively described as the scattering of short-lived quasiparticles on local impurities, in close analogy to Friedel oscillations in a Fermi liquid. This is in contrast to the strongly-coupled unidirectional stripes revealed at high magnetic fields, or specific dopings, whose long correlation length indicates the onset of a true long-range order. In the present analysis we employed a perturbative expansion in the disorder strength: from its success we infer that the effects of the disorder are weak and should not strongly affect Γ. We therefore suggest that the finite lifetime of quasiparticles at low temperatures is due to inelastic processes, possibly enhanced by the interplay between charge and spin degrees of freedom characteristic of cuprates. Both STM and ARPES [59, 60] measurements clearly indicate that Γ rapidly increases with temperature and underdoping. This finding suggests that a finite quasiparticle lifetime may have a significant role in the determination of the dome shape of the critical temperature of cuprates (see also SI-9). In particular, it is possible that the suppression of the critical temperature in underdoped samples could be due to a decreased quasiparticle lifetime.

In this section we show how to identify the main source of scattering and the three phenomenological parameters (${{\Delta }_{0}}$, Γ, and μ) by comparing equation (2) with STM experimental data. Our method consists in the analysis of a single point in momentum space. As shown in the text, the full momentum dependence can be predicted without any further fitting parameter.

The theoretical model (2) depends on the 2 × 2 matrix T_k, describing the effects of a local scatterer. The two main sources of scattering are local modulations of the chemical potential and of the pairing gap. Clearly, the former are diagonal in Nambu space and k independent, while the latter are off-diagonal and possess a d-wave symmetry. For completeness, we consider here four distinct scattering operators:

$$\begin{eqnarray}\begin{array}{rcl} T_{k}^{(1)} & = & \left( \begin{array}{ccccccccccccccc} 1 & 0 \\ 0 & -1 \\ \end{array} \right),\quad T_{k}^{(2)}=\left( \begin{array}{ccccccccccccccc} {{d}_{k}} & 0 \\ 0 & -{{d}_{k}} \\ \end{array} \right), \\ T_{k}^{(3)} & = & \left( \begin{array}{ccccccccccccccc} 0 & 1 \\ 1 & 0 \\ \end{array} \right),\quad T_{k}^{(4)}=\left( \begin{array}{ccccccccccccccc} 0 & {{d}_{k}} \\ {{d}_{k}} & 0 \\ \end{array} \right), \\ \end{array}\end{eqnarray} \tag{ 5 }$$

where ${{d}_{k}}={\rm cos} ({{k}_{x}})-{\rm cos} ({{k}_{y}})$ is a d-wave function. The operators $T_{k}^{(1)}$ and $T_{k}^{(4)}$ correspond respectively to local modulation of the chemical potential and of the pairing gap. All four perturbations respect time-reversal symmetry: in the present analysis we neglect the effects of local magnetic impurities, which may lead to short-ranged periodic spin modulations.

In figure 5 we isolate the effects of the free parameters of our theory by varying each of them independently. In figure 5(a) we vary the scattering matrix T_k among the four options of equation (5), and observe dramatic effects on the voltage-dependence of the resulting signal. In particular, we observe that at low voltages $V\lt {{\Delta }_{0}}$ the predicted signal is mainly anti-symmetric with respect to $V\to -V$ for modulations of the chemical potential (${{T}^{(1)}}$) and symmetric for modulations of the pairing gap (${{T}^{(4)}}$). Figure 5(b) shows that ${{\Delta }_{0}}$ controls the position of the peaks. Note however that the maxima are not located at $\pm {{\Delta }_{0}}$ (as often assumed in the literature), but rather at approximately $\pm 0.75{{\Delta }_{0}}$. As explained in SI-3, this is due to the fact that the STM signal is due to quasiparticles in a broad range of momenta (close to the antinodes), whose energy is necessarily smaller than ${{\Delta }_{0}}$. Figure 5(c) shows that the inverse quasiparticle lifetime Γ controls the width of the peaks and the amplitude of the zero-voltage-conductance. Finally, figure 5(d) shows that the chemical potential μ controls the relative intensity of the two peaks.

Zoom In Zoom Out Reset image size

We now move to the experimental data. The absolute value of the Fourier transformed signal $\mid {{g}_{{\rm exp} }}(q,V)\mid$ is shown in figure 5(e) at four q-points that are equivalent under the lattice symmetry group. As usual, the raw data is smoothed by averaging over a small region in q-space $\delta q\approx 0.03\times 2\pi$ to increase the signal-to-noise ratio. Note that, for wavevectors inside the Brillouin zone (green and black curves), the differential conductance is peaked at $V\approx \pm 15$ meV, while for larger wavevectors (red and blue curves) its maximum is at $V\approx 40$ meV. A similar behavior was observed in [47] and to date not explained. As shown in SI-10, this effect is probably related to the normalization procedure required to analyze the STM data.

As mentioned in the text, the nature of the dominant scattering matrix T_k can be deduced from the phase of the Fourier-transformed STM signal [37, 61]. However, in the raw data the phase also depends on the random position of the impurities r₀ and may vary across the sample, through the factor e^iqr₀ appearing in equation (2). Due to this random phase, the smoothing techniques presented above cannot be straightforwardly applied. To overcome this problem, we first divide the signal at each wavevector by the corresponding low-voltage phase, ${{{\rm e}}^{{\rm i}\phi (q)}}={{\sum }_{\mid V\mid \lt {{V}_{{\rm max} }}}}g(q,V)/\mid g(q,V)\mid$, where ${{V}_{{\rm max} }}=10$ meV is an arbitrary cutoff (see also SI-6 for a different choice of ${{{\rm e}}^{{\rm i}\phi (q)}}$ leading to similar results). This allows us to subsequently average over $\delta q$ and isolate the real and imaginary components of the signal, as shown in figures 5(e)–(g). The imaginary part is small, indicating that the phase of the signal is voltage independent, in agreement with our model of scattering from time-independent perturbations. The real part is analogous to the signal observed in Bi2212 [4] and is now suitable for a direct comparison with the theoretical predictions (figures 5(a)–(d)).

At low voltages the experimental signal is symmetric with respect to $V\to -V$, demonstrating that the scattering is dominated by local modulations of the gap (${{T}^{(4)}}$) [37, 61]. Remarkably, the same impurity model also describes localized magnetic vortices (where the pairing amplitude is strongly suppressed), in whose vicinity the incommensurate order was first observed [3].

At higher voltages, all four spectra show pronounces peaks at positive and negative voltages. The position of the peaks ($V\approx \pm 15$ meV) indicates that the pairing gap is ${{\Delta }_{0}}\approx 20$ meV. From the width of the peaks and their relative height, we deduce that $\Gamma \approx 8$ meV and $\mu \approx -5$ meV. By repeating this approach for the other three samples (not shown here) we obtain the parameters presented in table 1. The values of the gaps obtained by the present analysis coincide with the superconducting gaps found in ARPES measurements on the same material (see [62] and references therein). Surprisingly, these experiments showed strong deviations of the gap from a simple d-wave form, leading to a two-fold-larger gap around the antinodes (${{\Delta }_{{\rm antinode}}}\approx 40$ meV). This larger gap, which may be related to a competing order, is not observed in STM experiments (see figure 1(a)). This point deserves further investigation.

We are grateful to Mike Boyer, Kamalesh Chatterjee, Eric Hudson, Jennifer Hoffman, and Doug Wise for giving us access to their unpublished experimental data. We also acknowledge Mehrtash Babadi, Erez Berg, Lucio Braicovich, Andrea Damascelli, JC Séamus Davis, Thierry Giamarchi, Jennifer Hoffman, Yachin Ivry, Marc-Henri Julien, Amit Kanigel, Malcolm Kennett, Nimrod Moiseyev, Elisabeth Nowadnick, Daniel Podolsky, Subir Sachdev, Jeff Sonier, and Philipp Strack for many useful discussions. This research is supported by THE ISRAEL SCIENCE FOUNDATION (grant no. 1542/14), NSF grant DMR-1308435, Harvard-MIT CUA, and AFOSR New Quantum Phases of Matter MURI.