Abstract
The quantum navigation problem of finding the time-optimal control Hamiltonian that transports a given initial state to a target state through quantum wind, that is, under the influence of external fields or potentials, is analyzed. By lifting the problem from the state space to the space of unitary gates realizing the required task, we are able to deduce the form of the solution to the problem by deriving a universal quantum speed limit. The expression thus obtained indicates that further simplifications of this apparently difficult problem are possible if we switch to the interaction picture of quantum mechanics. A complete solution to the navigation problem for an arbitrary quantum system is then obtained, and the behaviour of the solution is illustrated in the case of a two-level system.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
With the advances in the implementation of quantum technologies, the theoretical understanding of controlled quantum dynamics and, in particular, of their limits, is becoming increasingly important. One aspect of such limits that has been investigated extensively in the literature concerns the time-optimal manoeuvring of quantum states [1–18]. If the time-evolution is unconstrained (apart from a bound on the energy resource), then this amounts to finding the time-independent Hamiltonian that generates maximum speed of evolution. However, in general there can be a range of constraints that prohibits the implementation of such an elementary protocol, and various optimizations will have to be applied to determine time-dependent Hamiltonians that generate the dynamics achieving required tasks.
An important class of problems arising in this context is the identification of the time-optimal quantum evolution under the influence of external fields or potentials that cannot be easily eliminated in a laboratory. Solutions to such problems are indeed relevant to practical implementations of time-optimal controlled quantum dynamics because in real laboratories external influences (e.g, electromagnetic fields) are typically present. Problems of this kind can be thought of as representing the quantum counterpart of the classical Zermelo navigation problem of finding the time-optimal control that takes a ship from one location to another, under the influence of external wind or currents [19, 20]. Within the context of quantum Zermelo problems, there are two distinct questions that arise, namely, finding the time-optimal Hamiltonian (i) that generates a required unitary gate; and (ii) that transports a given initial state to a required target state. In the context of constructing a unitary gate, this problem was formulated in [21], and solved more recently in [22, 23]. The construction of the time-optimal Hamiltonian that transports a given initial state to a target state, on the other hand, is a priori more challenging (see also [24]), because (as shown below) this involves a variational problem with free boundaries. The purpose of the present paper is to derive the full solution to this latter problem for an arbitrary quantum system.
One way of addressing the quantum-state navigation problem is to work in the space of rays through the origin of the underlying Hilbert space (i.e. the complex projective space, or simply the 'state space'). Then the Schrödinger evolution generated by the background field gives rise to a Hamiltonian vector field on the state space, and the task at hand can be formulated as a Hamiltonian control problem, the solution of which is typically difficult to obtain. We are nevertheless able to go forward by exploiting certain subtle geometric structures of the unitary group, which in turn allows us to efficiently make use of the results obtained in [22, 23]. A remarkable feature of the solution that we obtain is that it is strikingly reminiscent of the analysis of quantum dynamics in the interaction-picture of Schwinger and Tomonaga [25]. On account of this observation we are able to revisit our analysis by employing a physical symmetry argument, rather than purely variational reasoning. As a consequence, a considerably simpler derivation of the solution emerges. In fact, it turns out that by invoking the line of thinking behind the Schwinger–Tomonaga theory, a straightforward solution can be found of closely-related and apparently difficult problems in geometry [26, 27]. For an illustration we conclude the paper by presenting examples in the case of a two-level system.
Let us begin by stating more explicitly the Zermelo navigation problem for quantum states: For a given initial state 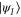 and a final target state
and a final target state 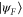 , the task of an experimentalist is to find the control Hamiltonian
, the task of an experimentalist is to find the control Hamiltonian 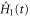 such that the total Hamiltonian
such that the total Hamiltonian 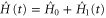 will generate the transformation
will generate the transformation 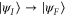 in the shortest possible time. Here
in the shortest possible time. Here 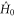 represents the Hamiltonian of the background field or potential that cannot be manipulated. Since the objective is to realize a time-optimal transformation (navigation), it is assumed that the available energy resource, which evidently has to be bounded, will be consumed fully. This translates into the 'full throttle' condition that the squared magnitude of the evolution speed generated by the control Hamiltonian
represents the Hamiltonian of the background field or potential that cannot be manipulated. Since the objective is to realize a time-optimal transformation (navigation), it is assumed that the available energy resource, which evidently has to be bounded, will be consumed fully. This translates into the 'full throttle' condition that the squared magnitude of the evolution speed generated by the control Hamiltonian 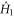 , which is given on account of the Anandan–Aharonov relation [28] by four times the variance
, which is given on account of the Anandan–Aharonov relation [28] by four times the variance 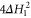 of
of 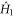 , is held fixed at all times at the maximum attainable value.
, is held fixed at all times at the maximum attainable value.
To illustrate the nature of the task involved, let us first consider a more elementary problem of Zermelo navigation on the plane 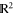 , with constant (in space and in time) wind, represented by the vector
, with constant (in space and in time) wind, represented by the vector 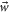 . Suppose that, departing from the origin o the desired destination is given by the endpoint of a vector
. Suppose that, departing from the origin o the desired destination is given by the endpoint of a vector 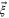 . To work out the time it takes to reach the destination, consider a circle whose radius is determined by the distance that can be reached with full speed over one unit of time. In the absence of wind this unit circle is clearly centred at the origin. However, under the influence of the wind the centre of the circle is shifted by
. To work out the time it takes to reach the destination, consider a circle whose radius is determined by the distance that can be reached with full speed over one unit of time. In the absence of wind this unit circle is clearly centred at the origin. However, under the influence of the wind the centre of the circle is shifted by  . For the moment let us assume that the wind is not dominant, i.e.
. For the moment let us assume that the wind is not dominant, i.e.  so that the origin remains inside the shifted circle. This configuration is schematically illustrated in figure 1. Under the influence of the wind, therefore, to reach the endpoint ξ of the vector
so that the origin remains inside the shifted circle. This configuration is schematically illustrated in figure 1. Under the influence of the wind, therefore, to reach the endpoint ξ of the vector 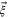 , it suffices to determine the distance
, it suffices to determine the distance 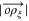 , where
, where 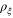 is the point of intersection of the vector
is the point of intersection of the vector 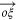 with the shifted circle. This follows on account of the fact that since it takes one unit of time to reach
with the shifted circle. This follows on account of the fact that since it takes one unit of time to reach 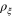 , it will take
, it will take 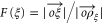 units of time to reach ξ. Elementary algebra then shows that the required time
units of time to reach ξ. Elementary algebra then shows that the required time 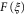 is given by the expression
is given by the expression
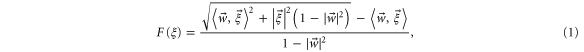
where 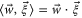 is the Euclidean inner product,
is the Euclidean inner product,  , and
, and 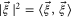 .
.
Figure 1. Unit circle in the wind. In the absence of the wind, the 'unit-time' circle is centred at the origin o. However, with the prevailing wind, with strength 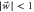 , the unit-time circle reachable from the origin is shifted in the direction of the wind. Since it takes one unit of time to reach
, the unit-time circle reachable from the origin is shifted in the direction of the wind. Since it takes one unit of time to reach 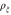 , reaching the target ξ will take
, reaching the target ξ will take 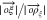 units of time.
units of time.
Download figure:
Standard image High-resolution imageThe foregoing analysis on 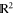 extends naturally to the general case of navigation on a Riemannian manifold of arbitrary dimension, albeit the Euclidean inner product
extends naturally to the general case of navigation on a Riemannian manifold of arbitrary dimension, albeit the Euclidean inner product 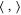 has to be replaced by the Riemannian one. This is because the total journey time can be decomposed into a large number of infinitesimal journey times, each on a tangent space of the manifold. In the case of optimal quantum navigation, we recall that the space of pure states is equipped with the unitary-invariant Fubini–Study metric [29–31]. The wind
has to be replaced by the Riemannian one. This is because the total journey time can be decomposed into a large number of infinitesimal journey times, each on a tangent space of the manifold. In the case of optimal quantum navigation, we recall that the space of pure states is equipped with the unitary-invariant Fubini–Study metric [29–31]. The wind  is then replaced by the infinitesimal Hamiltonian symplectic flow generated by
is then replaced by the infinitesimal Hamiltonian symplectic flow generated by 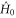 , whereas
, whereas 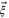 is some vector tangent to quantum state space. The total journey time T along a path on state space is given by the integral of
is some vector tangent to quantum state space. The total journey time T along a path on state space is given by the integral of 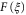 , where
, where 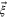 is the velocity vector. In particular, for the Zermelo problem,
is the velocity vector. In particular, for the Zermelo problem, 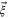 is generated by
is generated by  , and this implies that
, and this implies that 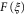 in the quantum context is given by a function of the variance
in the quantum context is given by a function of the variance 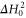 of
of 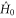 , the variance
, the variance 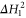 of
of 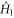 , and the covariance
, and the covariance  of the two Hamiltonians. The optimal control is obtained by minimizing T over all
of the two Hamiltonians. The optimal control is obtained by minimizing T over all 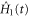 , subject to the full throttle constraint
, subject to the full throttle constraint 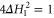 . The no-dominance condition on the wind is required in the case of a navigation problem on an open manifold such as
. The no-dominance condition on the wind is required in the case of a navigation problem on an open manifold such as 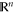 , since otherwise the target may never be reached. In the quantum context we are able to relax the requirement
, since otherwise the target may never be reached. In the quantum context we are able to relax the requirement  , since the manifold of pure states is compact, which means that if the wind against the shortest path is too strong, one can always go 'the other way around' to reach the target state (note incidentally that
, since the manifold of pure states is compact, which means that if the wind against the shortest path is too strong, one can always go 'the other way around' to reach the target state (note incidentally that 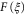 remains well defined in the limit
remains well defined in the limit 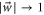 since
since 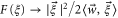 ).
).
The Hamiltonian control problem specified above is not straightforward to solve directly, and this leads us to employ an alternative approach based on the idea of lifting the problem from state space to the unitary group acting on the states. In fact, from a physical point of view this is more appealing, since, although we are seeking the time-optimal path on state space, physical implementations are always carried out by constructing the Hamiltonian that generates the desired unitary operator.
With this in mind, we proceed by considering a fibre space above the state space with the property that for any state 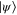 , the fibre above it consists of elements
, the fibre above it consists of elements  of the special unitary group fulfilling the condition that
of the special unitary group fulfilling the condition that 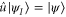 . Although our solution is applicable to both finite and infinite dimensional Hilbert spaces, to simplify the discussion let us assume that the Hilbert space is of finite dimension
. Although our solution is applicable to both finite and infinite dimensional Hilbert spaces, to simplify the discussion let us assume that the Hilbert space is of finite dimension 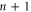 . The totality of such fibres, when bundled together, then forms the group SU
. The totality of such fibres, when bundled together, then forms the group SU 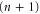 , which acts on the state space (the complex projective space
, which acts on the state space (the complex projective space 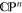 ). This configuration is illustrated in figure 2. Let
). This configuration is illustrated in figure 2. Let 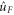 be an element of the fibre above the target state
be an element of the fibre above the target state 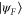 , i.e.
, i.e. 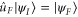 . Then the problem of finding the time-optimal transformation
. Then the problem of finding the time-optimal transformation  translates into the problem of constructing the unitary gate
translates into the problem of constructing the unitary gate 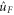 from the identity element
from the identity element 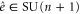 in the shortest possible time, under the influence of an external field. This translation of the problem helps us because the optimal Zermelo navigation for a specified unitary gate has been worked out recently [22, 23], and we can make use of the result in deducing the optimal control Hamiltonian for the state transfer; however, we encounter two difficulties: (a) the 'target' unitary gate
in the shortest possible time, under the influence of an external field. This translation of the problem helps us because the optimal Zermelo navigation for a specified unitary gate has been worked out recently [22, 23], and we can make use of the result in deducing the optimal control Hamiltonian for the state transfer; however, we encounter two difficulties: (a) the 'target' unitary gate 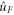 is not unique since a priori it can be any element of the fibre above
is not unique since a priori it can be any element of the fibre above 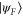 . In other words, if
. In other words, if 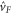 is any unitary operator that leaves the state
is any unitary operator that leaves the state 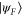 invariant, then the unitary gate
invariant, then the unitary gate 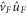 also satisfies the required condition
also satisfies the required condition 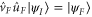 so we have to deal with a free final boundary; (b) the 'full throttle' condition
so we have to deal with a free final boundary; (b) the 'full throttle' condition 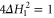 on state space is concerned with the evolution speed, whereas the condition used in [21–23] for unitary gates appears to be distinct since it concerns the Hilbert–Schmidt norm
on state space is concerned with the evolution speed, whereas the condition used in [21–23] for unitary gates appears to be distinct since it concerns the Hilbert–Schmidt norm 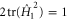 . In what follows we shall show that these two apparent issues evaporate once the relevant 'horizontality condition' is imposed on the control Hamiltonian.
. In what follows we shall show that these two apparent issues evaporate once the relevant 'horizontality condition' is imposed on the control Hamiltonian.
Figure 2. Lifting of the navigation problem. We construct a fibre space of unitary group elements above the state space with the property that any element 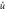 in the fibre above the state
in the fibre above the state 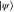 is projected down according to
is projected down according to 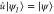 . Starting from the identity element
. Starting from the identity element 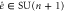 in the fibre above
in the fibre above  , the unitary group elements that can be reached in one unit of time under the influence of the 'wind'
, the unitary group elements that can be reached in one unit of time under the influence of the 'wind' 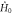 form a shifted unit sphere. The projection of the sphere onto the state space
form a shifted unit sphere. The projection of the sphere onto the state space 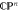 then determines the set of states reachable in that time. The furthest that one can transport the state is by moving away from
then determines the set of states reachable in that time. The furthest that one can transport the state is by moving away from 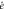 in the horizontal direction. There remain many horizontal directions, one of which is singled out by the boundary condition
in the horizontal direction. There remain many horizontal directions, one of which is singled out by the boundary condition 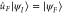 .
.
Download figure:
Standard image High-resolution imageTo see this we begin by noting that since 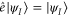 , the identity element
, the identity element 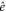 belongs to the fibre above the initial state
belongs to the fibre above the initial state  . In fact, the fibre above
. In fact, the fibre above 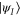 coincides with the totality of unitary group elements
coincides with the totality of unitary group elements 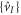 that leave the initial state
that leave the initial state 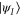 invariant. Intuitively, to reach from
invariant. Intuitively, to reach from 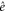 a target gate
a target gate 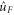 above
above 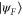 in a timely manner we would like to move away from
in a timely manner we would like to move away from 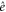 as quickly as possible, and this is achieved by manoeuvring horizontally, i.e. towards a direction that is orthogonal to the fibre. That is to say, the choice of the initial control Hamiltonian
as quickly as possible, and this is achieved by manoeuvring horizontally, i.e. towards a direction that is orthogonal to the fibre. That is to say, the choice of the initial control Hamiltonian  has to be such that
has to be such that 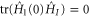 for all Hamiltonians
for all Hamiltonians 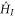 that leave the initial state invariant (i.e.
that leave the initial state invariant (i.e. 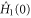 has to be orthogonal to all generators of
has to be orthogonal to all generators of 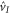 ). This suggests that the horizontality condition
). This suggests that the horizontality condition 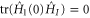 gives rise to the maximum evolution speed. To show this more explicitly we shall derive a kind of universal quantum speed limit. The statement of the result we shall establish is as follows: The squared speed of the evolution of a quantum state generated by a Hamiltonian
gives rise to the maximum evolution speed. To show this more explicitly we shall derive a kind of universal quantum speed limit. The statement of the result we shall establish is as follows: The squared speed of the evolution of a quantum state generated by a Hamiltonian 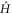 , as defined by Anandan and Aharonov [28], is bounded above by twice the Hilbert–Schmidt norm
, as defined by Anandan and Aharonov [28], is bounded above by twice the Hilbert–Schmidt norm 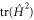 of the Hamiltonian, and the bound is attained if
of the Hamiltonian, and the bound is attained if 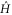 is horizontal. The implication of this result is that under the horizontality requirement the norm condition and the maximum speed condition are equivalent, and this resolves the issue (b) raised above. As a consequence, we are able to borrow the results of [22, 23] to deduce that the time-optimal control Hamiltonian
is horizontal. The implication of this result is that under the horizontality requirement the norm condition and the maximum speed condition are equivalent, and this resolves the issue (b) raised above. As a consequence, we are able to borrow the results of [22, 23] to deduce that the time-optimal control Hamiltonian 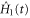 is necessarily of the form
is necessarily of the form
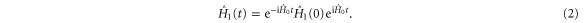
Notice that the horizontality condition is preserved under the adjoint action (2), which is indeed required since the full throttle condition has to be maintained throughout the operation.
The horizontality condition alone, of course, does not fix 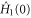 uniquely, since the constraint
uniquely, since the constraint  on
on  leaves
leaves 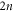 degrees of freedom. However, by demanding that the required gate should generate the target state
degrees of freedom. However, by demanding that the required gate should generate the target state  , which imposes
, which imposes 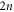 conditions, we are able to select a unique initial control Hamiltonian
conditions, we are able to select a unique initial control Hamiltonian 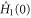 . In other words, the freedom in the boundary is eliminated by the horizontality condition
. In other words, the freedom in the boundary is eliminated by the horizontality condition 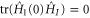 along with the boundary condition
along with the boundary condition 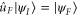 , and this resolves the issue (a) raised above.
, and this resolves the issue (a) raised above.
Before we turn to determining the initial control Hamiltonian 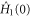 , and the amount of time T that is needed to reach the target state under the optimal control, let us discuss the claim above on the universal speed limit (see also [32]). From a physical point of view the claim is plausible if we make note of the following observation. Suppose that the Hamiltonian contains a vertical component tangent to the fibre that leaves the state below invariant. In this case, although energy is scarce, the experimentalist will be consuming energy that produces no work (except for shifting the overall phase). This is clearly not energy efficient. It follows that the optimal performance is ensured by eliminating vertical components altogether. A more precise derivation, which essentially follows from a standard result on complex projective spaces outlined, e.g., in Kobayashi and Nomizu [33] (see section 11.10), is given in the appendix.
, and the amount of time T that is needed to reach the target state under the optimal control, let us discuss the claim above on the universal speed limit (see also [32]). From a physical point of view the claim is plausible if we make note of the following observation. Suppose that the Hamiltonian contains a vertical component tangent to the fibre that leaves the state below invariant. In this case, although energy is scarce, the experimentalist will be consuming energy that produces no work (except for shifting the overall phase). This is clearly not energy efficient. It follows that the optimal performance is ensured by eliminating vertical components altogether. A more precise derivation, which essentially follows from a standard result on complex projective spaces outlined, e.g., in Kobayashi and Nomizu [33] (see section 11.10), is given in the appendix.
Having established the 'geodesic' curve (2) that minimizes the action  we are now in the position to identify the initial control
we are now in the position to identify the initial control 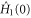 so that the target state is reached. To this end we observe that the form (2) of the solution is indicative of the analysis in the interaction picture of quantum mechanics, if we view
so that the target state is reached. To this end we observe that the form (2) of the solution is indicative of the analysis in the interaction picture of quantum mechanics, if we view 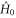 as the 'free' and
as the 'free' and 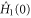 as the 'interaction' Hamiltonian. Alternatively stated, if we change from the 'rest frame' to the 'moving frame' on the state space according to the wind
as the 'interaction' Hamiltonian. Alternatively stated, if we change from the 'rest frame' to the 'moving frame' on the state space according to the wind 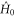 , then without the control Hamiltonian the initial state remains fixed, while the target state moves against the wind according to
, then without the control Hamiltonian the initial state remains fixed, while the target state moves against the wind according to 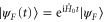 . Evidently, the state
. Evidently, the state 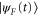 thus defined is the solution to the (nonrelativistic version of) the Tomonaga–Schwinger equation. In particular, standard results in the interaction-picture analysis [25] show that the time-ordered product of the unitary group generated by the Hamiltonian
thus defined is the solution to the (nonrelativistic version of) the Tomonaga–Schwinger equation. In particular, standard results in the interaction-picture analysis [25] show that the time-ordered product of the unitary group generated by the Hamiltonian 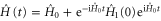 gives rise to the evolution equation of the form
gives rise to the evolution equation of the form
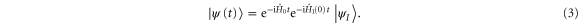
This result can also be verified directly (see also [22]) by differentiation: writing  , we find
, we find 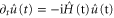 . As indicated above, to fix the initial condition
. As indicated above, to fix the initial condition  we need to make use of the boundary condition, which implies that
we need to make use of the boundary condition, which implies that
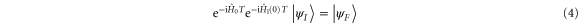
must hold for some T that is to be determined. Observe that there are 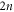 unknowns in
unknowns in 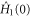 , and we have an additional unknown parameter T. The boundary condition (4) gives rise to
, and we have an additional unknown parameter T. The boundary condition (4) gives rise to 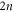 constraints. Together with the norm condition
constraints. Together with the norm condition 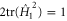 we are thus able to fix all the unknowns, and this in turn solves the quantum-state Zermelo navigation problem.
we are thus able to fix all the unknowns, and this in turn solves the quantum-state Zermelo navigation problem.
To proceed with this let us rewrite (4) in the form
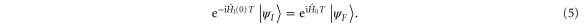
Although the transformation from (4) to (5) is in itself trivial, it sheds a different light on the problem at hand. As indicated above, if we transform to the moving frame generated by the wind such that the initial state remains stationary, then the objective becomes 'hitting' a moving target 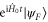 as quickly as possible. Exactly how long it will take to achieve this task depends on how fast the motion towards the target can be, but for a fixed speed the shortest time T achievable is attained by following the geodesic path on the state space joining
as quickly as possible. Exactly how long it will take to achieve this task depends on how fast the motion towards the target can be, but for a fixed speed the shortest time T achievable is attained by following the geodesic path on the state space joining 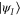 and
and 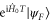 . On the other hand, the curve
. On the other hand, the curve  joining
joining 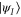 and
and 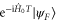 is a geodesic on the Fubini–Study manifold if and only if
is a geodesic on the Fubini–Study manifold if and only if 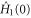 is horizontal, and this is indeed the situation we have in (5). To determine
is horizontal, and this is indeed the situation we have in (5). To determine 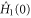 explicitly, let
explicitly, let 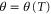 be the angular distance between
be the angular distance between 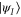 and
and 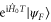 defined by the relation:
defined by the relation:

Evidently, the angular distance 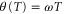 is given by the speed ω of the evolution generated by
is given by the speed ω of the evolution generated by 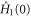 multiplied by the duration T of the journey, but the evolution speed is fixed on account of the condition
multiplied by the duration T of the journey, but the evolution speed is fixed on account of the condition 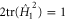 to
to  , so we deduce that
, so we deduce that

Since  ,
, 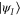 , and
, and  are given, we see therefore that the smallest positive root of (7) uniquely determines T. Once T is fixed, the optimal control Hamiltonian at time zero can be obtained explicitly by making use of the result in [10]:
are given, we see therefore that the smallest positive root of (7) uniquely determines T. Once T is fixed, the optimal control Hamiltonian at time zero can be obtained explicitly by making use of the result in [10]:

Note that without loss of generality we can adjust the overall phase such that  is real. With this convention, which is assumed in (8), one can easily verify that this Hamiltonian is indeed horizontal.
is real. With this convention, which is assumed in (8), one can easily verify that this Hamiltonian is indeed horizontal.
This completes the derivation of the solution to the quantum-state Zermelo navigation problem: the optimal control Hamiltonian is given by (2), where 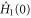 is given by (8) and where the parameter T is determined by (7). To gain further intuition on the behaviour of the solution, in figure 3 we plot the trajectories of the quantum state generated by the Hamiltonian
is given by (8) and where the parameter T is determined by (7). To gain further intuition on the behaviour of the solution, in figure 3 we plot the trajectories of the quantum state generated by the Hamiltonian 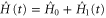 in the case of a two-level system. In particular, we show the time-optimal paths for a range of wind strengths, indicating for instance that if the head wind is too strong, then the optimal strategy is to switch the direction of the manoeuvre to turn the headwind into a tailwind. To investigate the minimum journey times associated with different wind strengths we have also considered a one-parameter family of winds
in the case of a two-level system. In particular, we show the time-optimal paths for a range of wind strengths, indicating for instance that if the head wind is too strong, then the optimal strategy is to switch the direction of the manoeuvre to turn the headwind into a tailwind. To investigate the minimum journey times associated with different wind strengths we have also considered a one-parameter family of winds 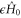 , corresponding to the setup shown in figure 3, and determined the optimal time
, corresponding to the setup shown in figure 3, and determined the optimal time 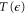 for a range of
for a range of  ; the result is shown in figure 4.
; the result is shown in figure 4.
Figure 3. Quantum Zermelo navigation. The 'wind' 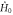 corresponds to an external field in the direction indicated by the red arrow; the associated flow lines are indicated by latitudinal circles. In this example, the wind is in the direction almost directly against the shortest path from
corresponds to an external field in the direction indicated by the red arrow; the associated flow lines are indicated by latitudinal circles. In this example, the wind is in the direction almost directly against the shortest path from 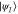 to
to 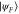 . When the strength of the wind is close to zero, the path generated by the optimal Hamiltonian closely follows the geodesic curve. However, as the strength of the wind is increased, the optimal path is drifted away from the geodesic curve. Once the wind is sufficiently strong, it is optimal to go the other way around; the loss generated by the additional journey length is compensated by the fact that the headwind has turned into a tailwind.
. When the strength of the wind is close to zero, the path generated by the optimal Hamiltonian closely follows the geodesic curve. However, as the strength of the wind is increased, the optimal path is drifted away from the geodesic curve. Once the wind is sufficiently strong, it is optimal to go the other way around; the loss generated by the additional journey length is compensated by the fact that the headwind has turned into a tailwind.
Download figure:
Standard image High-resolution imageFigure 4. Journey time on the Bloch sphere. The trajectories  sketched in figure 3 correspond to the wind Hamiltonian
sketched in figure 3 correspond to the wind Hamiltonian  for
for 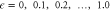 , for the choice of
, for the choice of 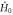 sketched therein. Here, journey time
sketched therein. Here, journey time 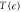 is plotted for a continuous range of
is plotted for a continuous range of  , showing that once the wind is sufficiently strong, by going the other way around, T can be reduced by turning headwind into a tailwind.
, showing that once the wind is sufficiently strong, by going the other way around, T can be reduced by turning headwind into a tailwind.
Download figure:
Standard image High-resolution imageIn summary, we have been able to deduce in closed form the solution to the quantum Zermelo problem in complete generality. Since the result obtained takes a rather simple form, we expect that a practical implementation is feasible in a number of realistic situations. Of course, for some applications the controllable degrees of freedom in the Hamiltonian can be limited, in which case additional constraints will have to be imposed in finding the optimal control—some steps towards this direction in the context of unitary gates have been initiated in [22]. In fact, further progress can again be made by switching to the interaction picture: If we write  for the N constraints on the control Hamiltonian, then in the moving frame the constraints will take for each k the form
for the N constraints on the control Hamiltonian, then in the moving frame the constraints will take for each k the form 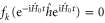 , where
, where  is the generator of the dynamics
is the generator of the dynamics 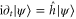 . The analysis of [8], for instance, can then be applied with essentially just one modification, namely, that the target state is moving. The initial control Hamiltonian can then be identified by adapting the strategy proposed in [18].
. The analysis of [8], for instance, can then be applied with essentially just one modification, namely, that the target state is moving. The initial control Hamiltonian can then be identified by adapting the strategy proposed in [18].
It is worth noting that the use of the interaction picture, or equivalently the switch to the moving frame, which allowed us to simplify the problem considerably, has implications beyond the quantum navigation problem considered here. In this connection we remark that if we endow the quantum state space with the metric of the form (1), then the resulting space is known as a Randers space (see [34]), which is an example of a Finsler space (for 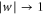 the space reduces to a Kropina space). In the literature of Finsler geometry it is known that every Zermelo navigation problem on a Riemannian manifold can be solved by finding geodesics of the corresponding Randers space [26]. The classification of spaces in terms of their curvatures is of particular importance in geometry, and in the case of Randers spaces the identification of constant curvature metrics has been obtained by solving the associated navigation problem when the wind is a conformal vector field with constant scale factor [27] (the field generated by a unitary motion belongs to this class, with vanishing scale factor). However, and with hindsight, the main theorem of [27] can be proven in essentially two lines by adopting the interaction picture, and this shows that in the present context a physical intuition can offer insights into a purely mathematical question. We conclude by remarking that an interesting generalization of the present problem is to consider the case under which the external influences contain noise. In such a situation, the idea of reaching a target pure state is no longer tenable, whereas reaching a particular mixed state might be feasible. Although there appears to be a surprisingly limited amount of work in the stochastic extensions of the classical Zermelo navigation problem (see [35] for an exception), extensions into the mixed-state domain are desirable for the designing and understanding of more robust controlled quantum dynamics.
the space reduces to a Kropina space). In the literature of Finsler geometry it is known that every Zermelo navigation problem on a Riemannian manifold can be solved by finding geodesics of the corresponding Randers space [26]. The classification of spaces in terms of their curvatures is of particular importance in geometry, and in the case of Randers spaces the identification of constant curvature metrics has been obtained by solving the associated navigation problem when the wind is a conformal vector field with constant scale factor [27] (the field generated by a unitary motion belongs to this class, with vanishing scale factor). However, and with hindsight, the main theorem of [27] can be proven in essentially two lines by adopting the interaction picture, and this shows that in the present context a physical intuition can offer insights into a purely mathematical question. We conclude by remarking that an interesting generalization of the present problem is to consider the case under which the external influences contain noise. In such a situation, the idea of reaching a target pure state is no longer tenable, whereas reaching a particular mixed state might be feasible. Although there appears to be a surprisingly limited amount of work in the stochastic extensions of the classical Zermelo navigation problem (see [35] for an exception), extensions into the mixed-state domain are desirable for the designing and understanding of more robust controlled quantum dynamics.
Acknowledgments
We thank Eva-Maria Graefe, Benjamin Russell, and Dmitry Savin for discussion and comments, and Martin Meier for support in producing figure 2.
Appendix. Derivation of the universal quantum speed limit
The purpose of this appendix is to offer a proof of the following claim in the paper: The squared speed of the evolution of a quantum state generated by a Hamiltonian 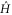 is bounded above by twice the Hilbert–Schmidt norm
is bounded above by twice the Hilbert–Schmidt norm  of the Hamiltonian, and the bound is attained if and only if
of the Hamiltonian, and the bound is attained if and only if  is horizontal.
is horizontal.
We begin by establishing some properties of the space of horizontal Hamiltonians. Recall that a Hamiltonian 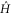 is horizontal with respect to some state
is horizontal with respect to some state 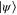 if and only if
if and only if 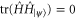 for all Hamiltonians
for all Hamiltonians 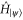 that leave
that leave 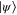 invariant. For simplicity, we fix the state
invariant. For simplicity, we fix the state 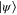 to be the one whose homogeneous coordinates are given by
to be the one whose homogeneous coordinates are given by 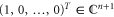 . It should be stressed, however, that the conclusions of the discussion below remain valid for any choice of
. It should be stressed, however, that the conclusions of the discussion below remain valid for any choice of 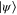 , owing to the homogeneous nature of the state space
, owing to the homogeneous nature of the state space 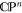 . Let us write
. Let us write  for the subgroup of SU
for the subgroup of SU 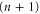 that leaves
that leaves 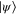 invariant and
invariant and 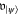 for the set of the corresponding generators (i.e. its Lie algebra). Then
for the set of the corresponding generators (i.e. its Lie algebra). Then 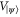 consists of all unit determinant matrices of the form
consists of all unit determinant matrices of the form
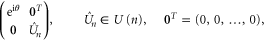
and 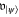 consists of all trace-free matrices of the form
consists of all trace-free matrices of the form
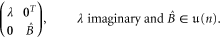
The orthogonal complement 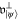 of this space with respect to the Hilbert–Schmidt norm coincides, up to a factor of i, with the space of horizontal Hamiltonians. Specifically, the set
of this space with respect to the Hilbert–Schmidt norm coincides, up to a factor of i, with the space of horizontal Hamiltonians. Specifically, the set 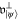 can be found by requiring that
can be found by requiring that
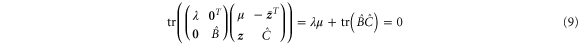
for all choices of λ and 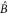 with
with 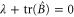 . Here we have parameterized the full Lie algebra
. Here we have parameterized the full Lie algebra  using an imaginary μ, a vector
using an imaginary μ, a vector 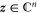 and
and  with
with 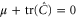 . It follows that
. It follows that 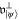 consists of all matrices of the form
consists of all matrices of the form
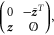
where 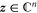 and
and 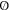 is a null matrix. As a consistency check, we note that this space has
is a null matrix. As a consistency check, we note that this space has 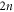 real dimensions, which of course is the same as the dimensionality of the state space
real dimensions, which of course is the same as the dimensionality of the state space 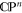 . It follows that if
. It follows that if 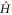 is a horizontal Hamiltonian, then
is a horizontal Hamiltonian, then
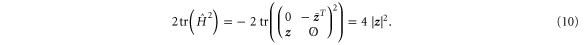
On the other hand, if 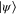 evolves according to the Schrödinger equation, then the squared speed (in the Fubini–Study metric) of its evolution is given, on account of the Anandan–Aharonov relation, by four times the variance of
evolves according to the Schrödinger equation, then the squared speed (in the Fubini–Study metric) of its evolution is given, on account of the Anandan–Aharonov relation, by four times the variance of 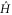 :
:
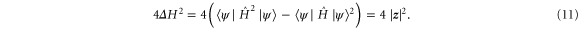
This establishes part of our claim: Namely, by comparing (10) and (11) we see that the square of the evolution speed equals twice the Hilbert–Schmidt norm 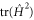 if
if 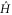 is horizontal. To complete the proof, note that any Hamiltonian
is horizontal. To complete the proof, note that any Hamiltonian 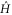 can be decomposed into vertical and horizontal parts, i.e. it can be written in the form
can be decomposed into vertical and horizontal parts, i.e. it can be written in the form
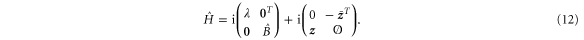
Then
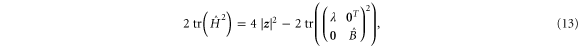
but the trace on the right hand side is strictly negative if the vertical part of 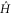 is nonzero. Therefore, the squared speed of evolution on state space, given by
is nonzero. Therefore, the squared speed of evolution on state space, given by 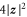 , is strictly smaller than
, is strictly smaller than 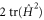 if the Hamiltonian contains a vertical component. This completes the proof of the claim.
if the Hamiltonian contains a vertical component. This completes the proof of the claim.








