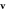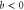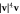Abstract
We study incompressible systems of motile particles with alignment interactions. Unlike their compressible counterparts, in which the order-disorder (i.e., moving to static) transition, tuned by either noise or number density, is discontinuous, in incompressible systems this transition can be continuous, and belongs to a new universality class. We calculate the critical exponents to 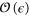 in an
in an  expansion, and derive two exact scaling relations. This is the first analytic treatment of a phase transition in a new universality class in an active system.
expansion, and derive two exact scaling relations. This is the first analytic treatment of a phase transition in a new universality class in an active system.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Emergent properties of interacting non-equilibrium systems are of widespread and fundamental interest. One of the simplest, but most striking, of these is the self-organized phenomenon of 'flocking'—that is, collective motion (CM) in large groups of motile organisms [1–10]. This phemenon is fascinating in part because its occurrence in two spatial dimensions requires the spontaneous breaking of a continuous symmetry, which is forbidden in thermal equilibrium by the Mermin–Wagner theorem [11]. It was initially hoped [2] that the transition into this novel state could be a continuous one belonging to a new universality class. However, it was subsequently realized, from both simulations and theoretical analysis [12–18] of the hydrodynamic equations [3–6], that as this putative continuous transition is approached from the ordered side, but before it can be reached, the homogeneous CM state becomes unstable to modulation of the density along the mean velocity. The transition from the homogeneous CM state (i.e., the ordered state) to the disordered state proceeds via two first order transitions: one from homogeneous to banded, the next from banded to disordered.
Since this instability requires density variations, we reason that the instability might be eliminated by making the system incompressible. In this paper, we show that, indeed, the order-disorder transition is continuous in an incompressible system, and belongs to a new universality class. We emphasize that the incompressibility is crucial for the existence of this continuous transition; in a compressible system, as shown in the theoretical analyses listed above [12–18], the continuous transition is always preempted by the aforementioned banding instability. In an incompressible system, such bands cannot form, since the density cannot vary. We demonstrate this by finding, in a dynamical renormalization group (DRG) analysis of the hydrodynamic equations for an incompressible active fluid in d spatial dimensions, a novel stable fixed point that controls the transition. This calculation is done to order 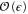 in an
in an 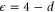 expansion; to the same order, we calculate the critical exponents of the transition. We also obtain two scaling laws relating these critical exponents which are valid to all orders in
expansion; to the same order, we calculate the critical exponents of the transition. We also obtain two scaling laws relating these critical exponents which are valid to all orders in  (i.e., exact).
(i.e., exact).
Our results are testable in both experiments and simulations. Three potential realizations are:
- (i)Systems with strong repulsive short-ranged interactions between the active particles. Incompressibility has, in fact, been assumed in, e.g., recent experimental studies on cell motility [19]. In such systems, the compressibility will be non-zero, but small. Hence, our incompressible results will apply out to very large length scales, or, equivalently, very close to the transition, but will ultimately crossover to the compressible behaviour (i.e., a small first order transition driven by the banding instability).
- (ii)Systems with long-ranged repulsive interactions; here, true incompressibility is possible. Long-ranged interactions are quite reasonable in certain contexts: birds, for example, can often see all the way across a flock [20].
- (iii)Motile colloidal systems in fluid-filled microfluidic channels. The forces exerted by the active particles are, of course, tiny compared to what would be needed to compress the background fluid, so that fluid is effectively incompressible. Since the active particles drag the background fluid with them, their motion is effectively incompressible as well. Indeed, experiments [21] show these systems do not exhibit the banding instability [12–18] found in all compressible active systems. This also suggests a numerical approach: simulating active particles moving through an incompressible fluid [22].
2. Generic model of incompressible active fluids
We formulate the most general hydrodynamic model for systems lacking both momentum conservation, and Galilean invariance, consistent with the symmetries of rotation and translation invariance, and the assumption of incompressibility. As the number density cannot fluctuate (by the assumption of incompressibility), the velocity field is the only hydrodynamic variable in the problem, which becomes soft as the transition is approached. Since the velocity is small near the transition, we can expand the equation of motion (EOM) in powers of the velocity. The symmetry constraints of translation and rotation invariance force the EOM valid at long wavelengths and times to take the form: [3–6]5
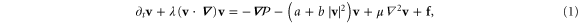
where the pressure 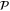 enforces the incompressibility condition
enforces the incompressibility condition  ,
, 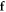 is a Gaussian 'white noise' with spatio-temporally Fourier transformed statistics:
is a Gaussian 'white noise' with spatio-temporally Fourier transformed statistics:
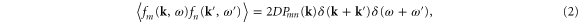
and 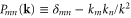 is the transverse projection operator. The compressible model [3–6] differs from this model only in the pressure
is the transverse projection operator. The compressible model [3–6] differs from this model only in the pressure  term, which is in this case a specified function of the density, and in that
term, which is in this case a specified function of the density, and in that 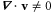 which allows a term proportional to (
which allows a term proportional to (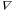 · v)v as well. One need also then give an EOM for the density, which is just the usual continuity equation .
· v)v as well. One need also then give an EOM for the density, which is just the usual continuity equation .
The EOM equation (1) reduces, when 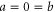 , to the classic model of a fluid forced at zero wavenumber treated by [23] (their 'model B'). For
, to the classic model of a fluid forced at zero wavenumber treated by [23] (their 'model B'). For  , it reduces to a simple, time-dependent Ginzburg–Landau [24, 25] dynamical model for an isotropic ferromagnet with long ranged dipolar interactions [26] 6
.
, it reduces to a simple, time-dependent Ginzburg–Landau [24, 25] dynamical model for an isotropic ferromagnet with long ranged dipolar interactions [26] 6
.
Because our system lacks Galilean invariance, 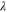 need not (and in general will not) equal one, and the terms
need not (and in general will not) equal one, and the terms  are allowed in the EOM. The latter terms are crucial as they make possible the existance of a polar ordered phase in an active system, which is not possible in a normal fluid.
are allowed in the EOM. The latter terms are crucial as they make possible the existance of a polar ordered phase in an active system, which is not possible in a normal fluid.
3. Novel universality class
At the mean field level, for 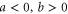 the system is in the ordered phase7
with
the system is in the ordered phase7
with 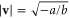 , and for
, and for  it is in the disordered phase with
it is in the disordered phase with 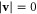 . To go beyond this mean field description, we employ the DRG method [23] near the order-disorder transition. To do so, we spatio-temporally Fourier transform equation (1), and project orthogonal to wavevector
. To go beyond this mean field description, we employ the DRG method [23] near the order-disorder transition. To do so, we spatio-temporally Fourier transform equation (1), and project orthogonal to wavevector  ; obtaining
; obtaining
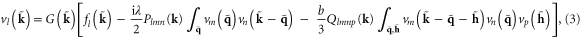
where we have adopted the reduced notations 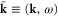 and
and 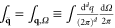 , and we have defined
, and we have defined 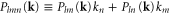 ,
,  , and the 'propagator'
, and the 'propagator' 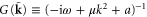 . This propagator is just the linearized response function giving the velocity induced, to linear order, by an external force.
. This propagator is just the linearized response function giving the velocity induced, to linear order, by an external force.
Graphical representations of the various terms in equation (3) are shown in figure 1. For an excellent and detailed exposition on the meaning and use of graphical techniques in the dynamical perturbative renormalization group (DRG) approach, we refer the reader to [23].
Figure 1. Graphical representations: (a)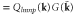 ; (b)
; (b) 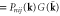 ; (c)
; (c) 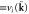 ; (d)
; (d) 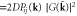 ; (e) the nonlinear term proportional to
; (e) the nonlinear term proportional to 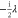 ; the line on the left represents
; the line on the left represents 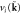 , while the two on the right represent
, while the two on the right represent 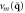 and
and 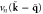 . (f) The nonlinear term proportional to
. (f) The nonlinear term proportional to 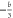 ; the line on the left represents
; the line on the left represents  , while the three on the right represent
, while the three on the right represent  ,
, 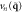 , and
, and 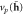 .
.
Download figure:
Standard image High-resolution imageWe now perform the standard DRG procedure [23], averaging over short wavelength degrees of freedom, and rescaling: 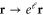 ,
, 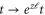 and
and 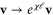 . Here the dynamical exponent z and the roughness exponent
. Here the dynamical exponent z and the roughness exponent  respectively relate time and velocity scales in the renormalized system to those in the physical problem. The rescaling exponents z and
respectively relate time and velocity scales in the renormalized system to those in the physical problem. The rescaling exponents z and 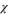 are, of course, completely arbitrary. A very convenient choice of them, however, is one that keeps the scale of velocity fluctuations in the renormalized system fixed. The values of z and
are, of course, completely arbitrary. A very convenient choice of them, however, is one that keeps the scale of velocity fluctuations in the renormalized system fixed. The values of z and 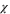 that we obtain by this criterion will, by construction, then give the scaling of the physical time scales and velocity fluctuations with length scale (hence the terms 'dynamical exponent' and 'roughness exponent').
that we obtain by this criterion will, by construction, then give the scaling of the physical time scales and velocity fluctuations with length scale (hence the terms 'dynamical exponent' and 'roughness exponent').
Our procedure is identical to the calculation for model B in [23], except for a modified propagator, and some additional Feynmann graphs due to the extra  nonlinearity in our problem. At the one loop level, the non-vanishing graphical contributions to the various coefficients in equation (3) are shown in figure 2. More details of the calculation are given in the supplemental materials (stacks.iop.org/NJP/17/042002/mmedia). We obtain, in d spatial dimensions, the following RG flow equations of the coefficients to one loop order and to linear order in
nonlinearity in our problem. At the one loop level, the non-vanishing graphical contributions to the various coefficients in equation (3) are shown in figure 2. More details of the calculation are given in the supplemental materials (stacks.iop.org/NJP/17/042002/mmedia). We obtain, in d spatial dimensions, the following RG flow equations of the coefficients to one loop order and to linear order in 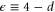 :
:
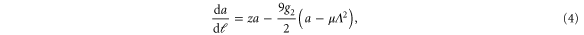
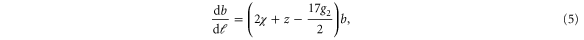
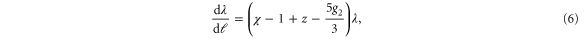
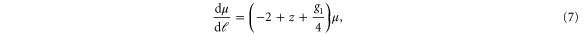
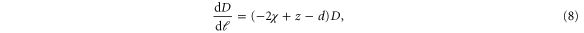
where we have defined dimensionless couplings:
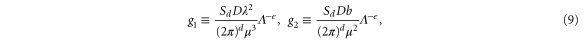
and where 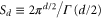 is the surface area of a unit sphere in d dimensions,
is the surface area of a unit sphere in d dimensions, 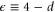 , and Λ is the ultraviolet wavevector cutoff which is of order the inverse of some 'microscopic' length (e.g., the typical distance between active particles). Since our interest is in the transition, we have, in the last four recursion relations (5)–(8), set a = 0, and have worked to linear order in a in (4). It is straightforward to verify that higher order terms in a affect none of our results up to and including linear order in
, and Λ is the ultraviolet wavevector cutoff which is of order the inverse of some 'microscopic' length (e.g., the typical distance between active particles). Since our interest is in the transition, we have, in the last four recursion relations (5)–(8), set a = 0, and have worked to linear order in a in (4). It is straightforward to verify that higher order terms in a affect none of our results up to and including linear order in 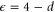 .
.
Figure 2. Non-vanishing diagrams at the one-loop level. Diagrams (a)–(d) contribute to a, b, λ and  respectively.
respectively.
Download figure:
Standard image High-resolution imageNow we derive coupled, closed recursion relations for 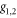 from the recursion relations (4–8). We begin by taking the natural logarithm of our definitions equation (9) of
from the recursion relations (4–8). We begin by taking the natural logarithm of our definitions equation (9) of 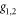 :
:
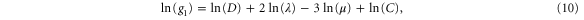
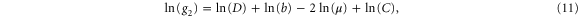
where we have defined the constant 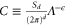 , which is 'constant' in the sense that it does not change upon renormalization. Differentiating both sides of (10) and (11) with respect to RG time ℓ therefore gives
, which is 'constant' in the sense that it does not change upon renormalization. Differentiating both sides of (10) and (11) with respect to RG time ℓ therefore gives
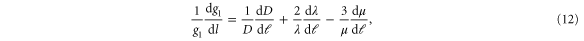
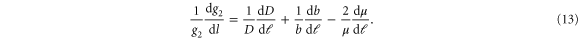
Plugging the recursion relations (5)–(8) on the right-hand side of (12) and (13), gathering terms, and multiplying (12) by g1 and (13) by g2 gives two closed flow equations for  for arbitrary
for arbitrary  and z:
and z:
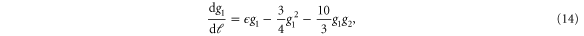

Although not necessary, it is convenient to make a special choice of z and 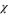 such that
such that 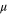 and D are kept fixed at their bare values (i.e,
and D are kept fixed at their bare values (i.e, 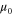 and D0, respectively). The advantage of the (completely arbitrary) choice to keep
and D0, respectively). The advantage of the (completely arbitrary) choice to keep 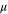 fixed is that the correlation length
fixed is that the correlation length 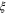 is determined by the ratio
is determined by the ratio  (specifically,
(specifically, 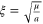 ). Hence, by keeping
). Hence, by keeping 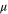 fixed, we can determine the scaling of
fixed, we can determine the scaling of 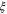 directly from the scaling of a, without having to worry about
directly from the scaling of a, without having to worry about  (since it is held fixed) at all. Likewise, keeping D fixed in addition keeps the fluctuations at the critical point unchanged (since those are controlled by the ratio
(since it is held fixed) at all. Likewise, keeping D fixed in addition keeps the fluctuations at the critical point unchanged (since those are controlled by the ratio 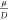 , which will, with this choice, be unchanged). This enables us to get the scaling of fluctuations at the critical point directly from the field rescaling
, which will, with this choice, be unchanged). This enables us to get the scaling of fluctuations at the critical point directly from the field rescaling 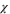 , which connects physical fluctuations to those in the renormalized system.
, which connects physical fluctuations to those in the renormalized system.
We will hereafter adopt this choice of z and  , which is
, which is
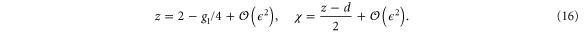
We will also hereafter use the subscript 0 to denote the bare (i.e., unrenormalized) values of the parameters.
Equation (4) now becomes
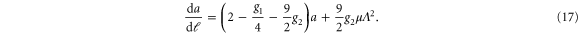
Equations (14), (15), (17) have a non-Gaussian fixed point in  :
:

which can be shown by analyzing the three recursion relations to be a stable attractor of all points on a two-dimensional surface (the 'critical surface' ) in the three-dimensional parameter space 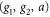 , but to be unstable with respect to displacements off this critical surface. The flows on the critical surface are illustrated in figure 3. This is exactly the topology of renormalization group flows that corresponds to a continuous phase transition with universal exponents controlled by the fixed point that's stable within the critical surface. Hence, we conclude that the order-disorder is generically continuous in incompressible active fluids. Furthermore, as far as we know, the fixed point we have obtained is novel, and thus the critical behaviour of incompressible active fluids belongs to a new universality class.
, but to be unstable with respect to displacements off this critical surface. The flows on the critical surface are illustrated in figure 3. This is exactly the topology of renormalization group flows that corresponds to a continuous phase transition with universal exponents controlled by the fixed point that's stable within the critical surface. Hence, we conclude that the order-disorder is generically continuous in incompressible active fluids. Furthermore, as far as we know, the fixed point we have obtained is novel, and thus the critical behaviour of incompressible active fluids belongs to a new universality class.
Figure 3. RG flows on the critical surface. Besides the unstable Gaussian fixed point (black diamond) and the stable fixed described in equation (18) (red square), there are two unstable fixed points: one at 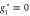 ,
, 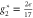 , which is the fixed point of an isotropic ferromagnet with long-ranged dipolar interactions [26] (purple circle), and one at
, which is the fixed point of an isotropic ferromagnet with long-ranged dipolar interactions [26] (purple circle), and one at 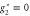 ,
, 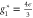 , which is the fixed point of a fluid forced at zero wavevector (model B of [23]) (blue triangle).
, which is the fixed point of a fluid forced at zero wavevector (model B of [23]) (blue triangle).
Download figure:
Standard image High-resolution image4. Critical exponents
As for equilibrium phase transitions [24, 25], there are a number of universal critical exponents associated with the order-disorder transition that we can obtain from this RG analysis. Readers interested in a more thorough discussion of these exponents, and their derivation from the renormalization group recursion relations, are referred to any one of a number of excellent textbooks (e.g., [24, 25]) that discuss this topic in far more detail than space allows us here. Suffice it to say that all of the analysis we present here is entirely standard in the study of critical phenomena.
All of these universal critical exponents are related to experimentally measurable correlation and response functions of the active fluid. For example, several of them can be obtained from the two point velocity correlation function  , which depends on bare parameters b0,
, which depends on bare parameters b0, 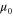 , D0, and
, D0, and  and, most importantly, the proximity to the phase transition
and, most importantly, the proximity to the phase transition  , where a0c is the value of a0 at the transition. We will show in a moment that the RG predicts that this correlation function has a scaling form for large r near the transition:
, where a0c is the value of a0 at the transition. We will show in a moment that the RG predicts that this correlation function has a scaling form for large r near the transition:
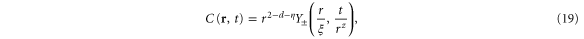
where the scaling functions 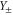 in equation (19) are different on the disordered (+) and ordered (-) sides of the transition, because the system is in different phases in the two cases. On the disordered side , we expect
in equation (19) are different on the disordered (+) and ordered (-) sides of the transition, because the system is in different phases in the two cases. On the disordered side , we expect 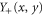 to decay exponentially with both x and y, while on the ordered side,
to decay exponentially with both x and y, while on the ordered side, 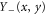 has a more complicated scaling behaviour that we will discuss elsewhere [32]. Two of the universal critical exponents,
has a more complicated scaling behaviour that we will discuss elsewhere [32]. Two of the universal critical exponents, 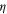 and z, are displayed explicitly in (19). A third, the so called 'correlation length exponent'
and z, are displayed explicitly in (19). A third, the so called 'correlation length exponent' 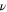 , is implicit in the correlation length
, is implicit in the correlation length 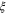 appearing in (19), which diverges as the transition is approached. In an experiment or simulation, one can approach the transition by tuning any one of many microscopic control parameters s (e.g.,
appearing in (19), which diverges as the transition is approached. In an experiment or simulation, one can approach the transition by tuning any one of many microscopic control parameters s (e.g., 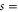 mean density or noise strength). The RG then predicts that the correlation length
mean density or noise strength). The RG then predicts that the correlation length 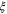 diverges algebraically with this control parameter as the transition is approached:
diverges algebraically with this control parameter as the transition is approached:
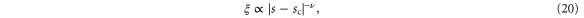
where 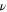 is a universal exponent and sc is the value of the control parameter at which the transition occurs.
is a universal exponent and sc is the value of the control parameter at which the transition occurs.
Another standard universal critical exponent is the 'order parameter exponent' 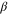 , which characterizes the growth of the order parameter (in our case, the mean velocity
, which characterizes the growth of the order parameter (in our case, the mean velocity 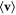 ):
):
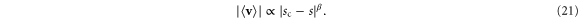
The final two exponents characterize the response, near or at the transition, of the system to a weak external field  ; that is, simply adding a small constant vector
; that is, simply adding a small constant vector 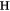 to the rhs of (1). On the disordered side of the transition, we expect linear response:
to the rhs of (1). On the disordered side of the transition, we expect linear response:

with the susceptibility  (which should not be confused with the 'roughness' exponent
(which should not be confused with the 'roughness' exponent 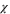 introduced earlier) diverging with a universal exponent
introduced earlier) diverging with a universal exponent 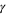 as the transition is approached from the disordered side:
as the transition is approached from the disordered side:
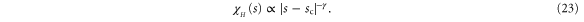
One can also ask about the response to this field right at the transition 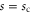 . This defines the final universal exponent δ, via:
. This defines the final universal exponent δ, via:
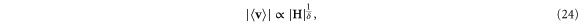
where  is in the same direction as the external field
is in the same direction as the external field  .
.
All of the scaling laws we have just specified are, of course, the leading order behaviour near the transition. Corrections to this themselves obey a scaling law, characterized by a 'correction to scaling exponent' 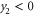 ; for example
; for example
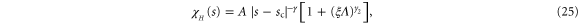
where A is a non-universal constant.
We will now use the RG to derive all of these scaling laws, and calculate, to linear order in 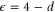 , the values of the universal exponents.
, the values of the universal exponents.
We begin by noting that the exponential runaway from the critical surface in the unstable direction near the stable fixed point (18) grows like 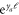 , with the exponent
, with the exponent
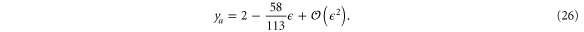
This eigenvalue determines the critical exponent 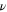 governing the critical behaviour of the velocity correlation length
governing the critical behaviour of the velocity correlation length 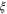 . In addition, the smaller (in magnitude) of the two negative eigenvalues of the critical fixed point gives the 'correction to scaling exponent' y2 [24]; we find
. In addition, the smaller (in magnitude) of the two negative eigenvalues of the critical fixed point gives the 'correction to scaling exponent' y2 [24]; we find 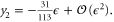
To show how ya determines  , and to derive the scaling law (19), we use the RG to connect the original
, and to derive the scaling law (19), we use the RG to connect the original 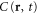 to that of the rescaled system:
to that of the rescaled system:
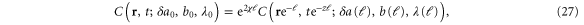
where we have not displayed 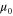 and D0, since they are kept fixed in the RG. By choosing
and D0, since they are kept fixed in the RG. By choosing 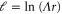 , and using
, and using 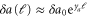 , we can obtain from this a scaling form for large r:
, we can obtain from this a scaling form for large r:
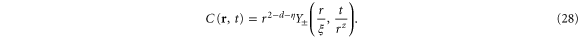
In particular, the equal time correlation function scales as 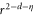 . In equation (28), the exponent
. In equation (28), the exponent 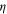 is given by
is given by
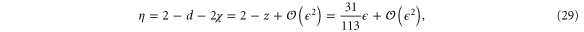
the scaling functions 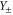 by
by
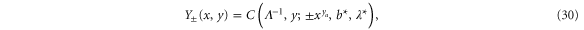
where b* and 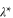 are the nonzero fixed values of
are the nonzero fixed values of 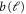 and
and 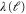 , respectively, and the diverging correlation length
, respectively, and the diverging correlation length 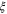 by
by 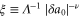 , where the correlation length exponent
, where the correlation length exponent
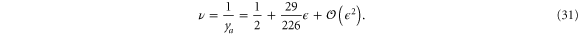
In our expression for the  expansions for
expansions for 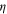 , we have replaced
, we have replaced 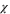 and z by their values at the fixed point (18), which is valid given that r is large and the system is sufficiently close to the transition. We do so consistently when calculating other exponents as well. The first line of equation (29) is exact (i.e., independent of the
and z by their values at the fixed point (18), which is valid given that r is large and the system is sufficiently close to the transition. We do so consistently when calculating other exponents as well. The first line of equation (29) is exact (i.e., independent of the  -expansion), as it is simply the definition of
-expansion), as it is simply the definition of  .
.
As discussed earlier, the order-disorder transition can be driven by tuning any one of many microscopic control parameters (e.g., density or noise strength). Whatever control parameter s is tuned, we expect 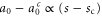 by analyticity near sc, where sc is the value of the control parameter s at the transition. As a result, the velocity correlation length
by analyticity near sc, where sc is the value of the control parameter s at the transition. As a result, the velocity correlation length 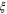 just defined diverges as
just defined diverges as 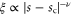 as any control parameter s is tuned.
as any control parameter s is tuned.
Now we calculate the magnitude of the order parameter in the ordered state near the critical point. The RG connects the average velocity of the original system and that of the rescaled system with the relation

This relation holds for all ℓ. To make the best possible use of it, we will choose ℓ such that 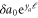 is of order 1. Therefore, ℓ is large since
is of order 1. Therefore, ℓ is large since 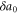 is small near the critical point, and hence, both
is small near the critical point, and hence, both 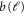 and
and 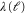 flow to their nonzero fixed values. Therefore, the quantity
flow to their nonzero fixed values. Therefore, the quantity 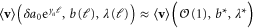 should be
should be 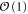 , and is in any case independent of the bare parameters, in particular a0. Hence, all the singular dependence on
, and is in any case independent of the bare parameters, in particular a0. Hence, all the singular dependence on  on the rhs of the equality (32) (indeed, all of the dependence on the bare parameters) is contained in the exponential (which depends in particular on
on the rhs of the equality (32) (indeed, all of the dependence on the bare parameters) is contained in the exponential (which depends in particular on 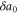 since the choice of ℓ that makes
since the choice of ℓ that makes  obviously does). This implies
obviously does). This implies 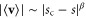 with
with
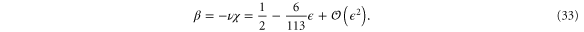
The first equality in this expression, which is exact, can be rewritten in terms of  using the definition of
using the definition of 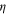 embodied in the first equality of (29), giving the exact hyperscaling relation
embodied in the first equality of (29), giving the exact hyperscaling relation

In this respect, our system is similar to equilibrium systems, in which (34) also holds [25].
We study next the response of the system to a weak external field 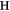 ; that is, simply adding a small constant vector
; that is, simply adding a small constant vector  to the rhs of (1). In this case, the RG leads to the scaling relation
to the rhs of (1). In this case, the RG leads to the scaling relation
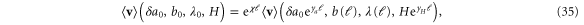
where 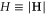 and yH is the RG eigenvalue of the external field H at the fixed point (18). As there are no one loop graphical corrections to the external field, we can obtain yH to
and yH is the RG eigenvalue of the external field H at the fixed point (18). As there are no one loop graphical corrections to the external field, we can obtain yH to  by simple power counting, which gives
by simple power counting, which gives
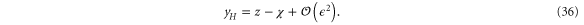
Again choosing ℓ such that 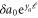 is of order 1, we obtain
is of order 1, we obtain
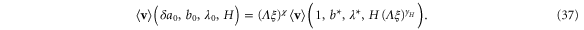
Since the expectation value on the right-hand side is evaluated in a system far from its critical region (since 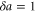 ), we expect linear response to the external field on that side with an order one susceptibility. Hence
), we expect linear response to the external field on that side with an order one susceptibility. Hence

which implies a linear susceptibility 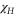 which diverges as
which diverges as  with
with
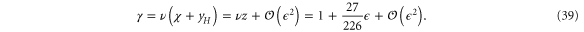
Note that equations (29), (39) seem to suggest that 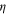 and
and  satisfy Fisher's scaling law
satisfy Fisher's scaling law 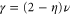 . However, since our system is out of equilibrium and thus the fluctuation dissipation theorem is not expected to hold, we do not expect Fisher's scaling law to hold; indeed, the
. However, since our system is out of equilibrium and thus the fluctuation dissipation theorem is not expected to hold, we do not expect Fisher's scaling law to hold; indeed, the 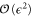 terms probably violate it. The first line of equation (39) is exact, however, and can be used to derive another scaling law, as we will now show.
terms probably violate it. The first line of equation (39) is exact, however, and can be used to derive another scaling law, as we will now show.
Turning on a small field right at the transition, we can again relate then the average velocities of the original and the rescaled systems using equation (35). However,  now flows to 0 for large ℓ since the system is right at the critical point. Therefore, by choosing
now flows to 0 for large ℓ since the system is right at the critical point. Therefore, by choosing  , we obtain the H-dependence of
, we obtain the H-dependence of 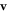 :
:
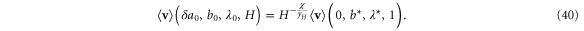
Again, all of the dependence on bare model parameters is now contained in the prefactor 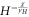 . Comparing (40) with our definition (24) of the critical exponent δ reveals that
. Comparing (40) with our definition (24) of the critical exponent δ reveals that  . Combining this with the exact first equalities in equations (33), (39), we obtain Widom's scaling relation
. Combining this with the exact first equalities in equations (33), (39), we obtain Widom's scaling relation
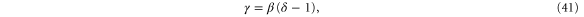
which is exact. Plugging the  -expansions of
-expansions of 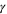 and
and 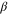 into this relation, we find
into this relation, we find
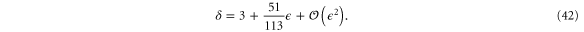
5. Numerical estimation
We can estimate the numerical values of the exponents in spatial dimension d = 3 as follows: We first choose a scaling relation satisfied by any three exponents (e.g., equation (23) for  ,
, 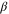 , and ν). We then determine numerical values for two of them (e.g., ν and
, and ν). We then determine numerical values for two of them (e.g., ν and 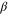 ) by simply setting
) by simply setting  in the
in the  -expansion for them, and dropping the unknown
-expansion for them, and dropping the unknown  terms. We now get the value of the third exponent (e.g.,
terms. We now get the value of the third exponent (e.g.,  ) by requiring that the scaling law (i.e., equation (23) ) hold exactly in d = 3. In this example, this gives
) by requiring that the scaling law (i.e., equation (23) ) hold exactly in d = 3. In this example, this gives 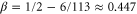 ,
, 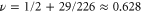 , and
, and 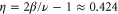 . Next, we take
. Next, we take 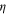 and
and 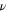 to be given by their respective
to be given by their respective  -expansions with
-expansions with 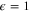 , and get
, and get  from the exact scaling relation. This gives:
from the exact scaling relation. This gives: 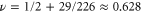 ,
, 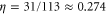 , and
, and 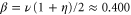 . Finally, we take
. Finally, we take  and
and 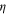 from their
from their  -expansions, and get
-expansions, and get 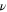 from the exact scaling relation, obtaining
from the exact scaling relation, obtaining 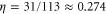 ,
, 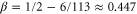 , and
, and 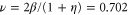 .
.
Note that each exponent gets two possible values in this approach: one from directly setting  in the
in the  -expansion, and another by obtaining the exponent from the exact scaling relation in d = 3.
-expansion, and another by obtaining the exponent from the exact scaling relation in d = 3.
Applying the same approach to Widom's exact scaling relation (i.e., equation (30)) and the three associated exponents 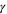 ,
, 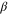 , and δ gives the possible values:
, and δ gives the possible values: 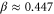 or
or 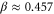 ,
, 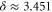 or
or  , and
, and  or
or 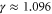 .
.
So if we look at the range of values we have found for each of the exponents, we have 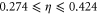 ,
, 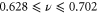 ,
,  ,
, 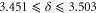 , and
, and  . Assuming, as seems reasonable (and as is true for, e.g., the critical exponents for the equilibrium
. Assuming, as seems reasonable (and as is true for, e.g., the critical exponents for the equilibrium 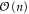 model [25]), that the correct values lie within the range spanned by the different approaches we have used here, we can conclude that, in spatial dimension d = 3, the critical exponents are as shown in the second column of table 1.
model [25]), that the correct values lie within the range spanned by the different approaches we have used here, we can conclude that, in spatial dimension d = 3, the critical exponents are as shown in the second column of table 1.
Table 1. Comparisons between the critical exponents obtained in this work and other models in spatial dimension d = 3.
| Exponents | Incomp. active fluids | Heisenberg model [26] | Heisenberg with dipolar interactions [27] |
|---|---|---|---|
| η | 0.35 ± 0.08 | 0.033 ± 0.004 | 0.023 ± 0.015 |
| β | 0.43 ± 0.03 | 0.3645 ± 0.0025 | 0.38 ± 0.02 |
| δ | 3.48 ± 0.03 | 4.803 ± 0.037 | 4.45 ± 0.04 |
| γ | 1.11 ± 0.01 | 1.386 ± 0.004 | 1.37 ± 0.02 |
| ν | 0.67 ± 0.04 | 0.705 ± 0.003 | 0.69 ± 0.02 |
Comparing the critical exponents with the known values for the two equilibrium analogs of our system: the three-dimensional, three component Heisenberg model (i.e., the 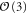 model) with and without dipolar interactions (third and fourth columns respectively in table 1), we see that
model) with and without dipolar interactions (third and fourth columns respectively in table 1), we see that 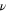 and
and 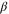 are very close in all three models. The situation is a little better for
are very close in all three models. The situation is a little better for 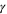 and δ. The biggest difference, however, is clearly in
and δ. The biggest difference, however, is clearly in  , which is much larger in the incompressible active fluid. Thus experiments to determine this exponent, which, as can be seen from equation (17), can be deduced from velocity correlations right at the critical point, will provide the clearest and most dramatic evidence for the non-equilibrium nature of this system, and the novelty of its universality class.
, which is much larger in the incompressible active fluid. Thus experiments to determine this exponent, which, as can be seen from equation (17), can be deduced from velocity correlations right at the critical point, will provide the clearest and most dramatic evidence for the non-equilibrium nature of this system, and the novelty of its universality class.
The values of the exponents in d = 2 obviously can not be reliably estimated quantitatively from the  expansion. We do note, however, that the ordered state is expected to exist and to have true long-ranged order. This is clear since true long-ranged order exists even in the compressible problem, which obviously has more fluctuations than the incompressible problem we have studied here. Hence, we do not expect this problem to be like the equilibrium
expansion. We do note, however, that the ordered state is expected to exist and to have true long-ranged order. This is clear since true long-ranged order exists even in the compressible problem, which obviously has more fluctuations than the incompressible problem we have studied here. Hence, we do not expect this problem to be like the equilibrium 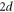 XY model, in which [28] the ordered state only has quasi-long-ranged order (i.e., algebraically decaying correlations). We therefore do not expect 2d incompressible active fluids to exhibit any of the singular behaviour of exponents found in the 2d equilibrium XY model; in particular, there is no reason to expect
XY model, in which [28] the ordered state only has quasi-long-ranged order (i.e., algebraically decaying correlations). We therefore do not expect 2d incompressible active fluids to exhibit any of the singular behaviour of exponents found in the 2d equilibrium XY model; in particular, there is no reason to expect 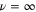 . Beyond this, there is little we can say quantitatively about d = 2 beyond the expectation that the critical exponents
. Beyond this, there is little we can say quantitatively about d = 2 beyond the expectation that the critical exponents 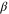 ,
, 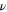 ,
, 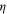 , δ, and
, δ, and 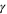 should be further from their mean field values
should be further from their mean field values 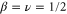 ,
, 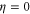 ,
, 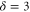 , and
, and 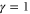 than they are in d = 3. This implies that in d = 2,
than they are in d = 3. This implies that in d = 2, 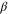 will be smaller, and the four other exponents will be bigger, than the values quoted above for d = 3. We also note that the exact scaling relations equations (34), (41) will hold in d = 2, and that all of the exponents will be universal (i.e., the same for all incompressible active fluids) in d = 2.
will be smaller, and the four other exponents will be bigger, than the values quoted above for d = 3. We also note that the exact scaling relations equations (34), (41) will hold in d = 2, and that all of the exponents will be universal (i.e., the same for all incompressible active fluids) in d = 2.
6. Conclusion and outlook
We have studied the order-disorder transition in incompressible active fluids using a dynamical  expansion. This is the first study of the static to moving phase transition in active matter to go beyond mean-field theory, and include the effects of fluctuations on the transition. We find a stable non-Gaussian fixed point, which implies a continuous transition, whose critical exponents were calculated to
expansion. This is the first study of the static to moving phase transition in active matter to go beyond mean-field theory, and include the effects of fluctuations on the transition. We find a stable non-Gaussian fixed point, which implies a continuous transition, whose critical exponents were calculated to 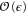 . This fixed point is new, and all of the critical exponents differ from those found for any previously known phase transition. Therefore, the universality class of this transition is new. In addition, we found that among the five critical exponents we calculated, there are two exact scaling relations which are the same as those in equilibrium ferromagnetic transitions. This is despite the fact that our system is fundamentally nonequilibrium, and that the universality class of its transition is new. Furthermore, we connected our model with two classic universality classes discovered in the early days of the renormalization group, namely the randomly stirred fluid model [23], and the dipolar ferromagnet model [26] (see figure 3). Specifically, we now know that the two fixed points associated to the two classic universality classes are unstable in the combined model we considered here.
. This fixed point is new, and all of the critical exponents differ from those found for any previously known phase transition. Therefore, the universality class of this transition is new. In addition, we found that among the five critical exponents we calculated, there are two exact scaling relations which are the same as those in equilibrium ferromagnetic transitions. This is despite the fact that our system is fundamentally nonequilibrium, and that the universality class of its transition is new. Furthermore, we connected our model with two classic universality classes discovered in the early days of the renormalization group, namely the randomly stirred fluid model [23], and the dipolar ferromagnet model [26] (see figure 3). Specifically, we now know that the two fixed points associated to the two classic universality classes are unstable in the combined model we considered here.
Our predictions on the critical exponents can be tested in motile systems (both experimental and simulated) with strong repulsive interactions between the particles, e.g., in bacterial suspensions like those studied in [19, 29], provided that the system can be tuned to reach the critical point. The exponent 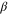 can be determined by measuring the average velocity. The exponents
can be determined by measuring the average velocity. The exponents 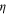 and the correlation length (which determines
and the correlation length (which determines 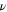 ) can be obtained by the velocity correlation functions. The exponents
) can be obtained by the velocity correlation functions. The exponents  and δ can be obtained by measuring the response of the average velocity to an external perturbation. In magnetotactic bacteria; the perturbation can be a magnetic field [30], in chemotactic bacteria, it can be a nutrient gradient [31].
and δ can be obtained by measuring the response of the average velocity to an external perturbation. In magnetotactic bacteria; the perturbation can be a magnetic field [30], in chemotactic bacteria, it can be a nutrient gradient [31].
Future theoretical work [32] on this problem will include working out in quantitative detail the cutoff of the continuous transition by the banding instability in systems with a small, but non-zero, compressibility.
Acknowledgments
JT thanks Nicholas Guttenberg for explaining how to simulate systems with long-ranged interactions. He also thanks the Department of Physics, University of California, Berkeley, CA; the Max Planck Institute for the Physics of Complex Systems (MPI-PKS), Dresden, Germany; the Aspen Center for Physics, Aspen, CO; the Isaac Newton Institute, Cambridge, UK; the Kavli Institute for Theoretical Physics, Santa Barbara, CA; and the Department of Bioengineering, Imperial College, London, UK for their hospitality while this work was underway. He also thanks the US NSF for support by awards #EF-1137815 and #1006171; and the Simons Foundation for support by award #225579. LC acknowledges support by the National Science Foundation of China (under Grant No. 11474354) and the Fundamental Research Funds for the Central Universities (under Grant No. 2013XK04). CFL thanks the MPI-PKS where the early stage of this work was performed.
Footnotes
- 5
- 6
The connection between our problem and the dipolar magnet is that the long-ranged dipolar interaction in magnetic systems couples to, and therefore suppresses, the longitudinal component of the magnetization. See [26] for more details.
- 7
When
 , a higher order, stabilizing fifth order term
, a higher order, stabilizing fifth order term  must be added to the right-hand side of our model. In this case, the order-disorder transition is first order even in the incompressible model.
must be added to the right-hand side of our model. In this case, the order-disorder transition is first order even in the incompressible model.