Abstract
In this brief paper, we compare two frameworks for characterizing possible operations in quantum thermodynamics. One framework considers thermal operations—unitaries which conserve energy. The other framework considers all maps which preserve the Gibbs state at a given temperature. Thermal operations preserve the Gibbs state; hence a natural question which arises is whether the two frameworks are equivalent. Classically, this is true—Gibbs-preserving maps are no more powerful than thermal operations. Here, we show that this no longer holds in the quantum regime: a Gibbs-preserving map can generate coherent superpositions of energy levels while thermal operations cannot. This gap has an impact on clarifying a mathematical framework for quantum thermodynamics.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
The field of thermodynamics has recently seen a surge of activity [1–21], in large part because of the application of techniques from information theory to the subject. One of the key contributions has been a more precise definition of what thermodynamics is, and this has allowed us to derive more rigorous quantitative statements about the laws of thermodynamics. Traditionally, a number of processes such as isothermal expansion or adiabatic processes were considered allowable thermodynamical operations, but the precise nature of what was allowed was never defined. Thermodynamics was considered to consist of crude control of systems, but as experimental control has improved, what constitutes a thermal process and what is considered to be disallowed was unclear.
However, once we define the allowable processes that constitute the field of thermodynamics, we can explore the implications. What's more, we can explore what happens in regimes which had previously been difficult to study, in particular, we can gain a better understanding of thermodynamics at the quantum level. In recent approaches to thermodynamics, one defines what thermodynamics is by specifying a set of state transformations which an experimenter is allowed to perform 'for free', i.e. at no work cost—such a framework is called a resource theory. However, there is more than one possible way to formulate the resource theory and it is crucial that we understand which ones are appropriate and under which circumstances. Among the various mathematical frameworks proposed to model thermodynamical operations, two have proven particularly useful, namely the resource theory of thermal operations and the Gibbs-preserving maps. Classically, these two frameworks are equivalent. If a transition between initial and final states block diagonal in their energy eigenbasis is possible by Gibbs-preserving maps, then it is also possible via thermal operations [11]. One might suppose that this equivalence holds for arbitrary quantum states. In this short paper, we show that this is not the case: Gibbs-preserving maps can perform transitions which thermal operations are incapable of.
Thermal operations. The resource theory of thermal operations has been extensively exploited to understand thermodynamics at the quantum level [3, 9, 11, 22, 23]. One is allowed to perform any arbitrary joint unitary operation, on a system and a heat bath at a given temperature T, which conserves the total energy on the joint state of the system and the bath. Thermal operations also include bringing in arbitrary systems which are in the Gibbs state at temperature T (with arbitrary Hamiltonians). Finally, thermal operations allow subsystems to be discarded for free, regardless of their state. Observe that thermal operations cannot change the Gibbs state into any other state [9, 11, 22]. What's more, the Gibbs state is the only state which has this property [17]. Gibbs states are thus the only state which can be allowed for free—if any other state were allowed, arbitrary state transformations would be possible.
Crucially, thermal operations are not capable of generating coherent superpositions of energy levels: a thermal operation must, by definition, commute with the total Hamiltonian, and thus cannot generate such a superposition starting from an energy eigenstate.
Gibbs-preserving maps. In the framework of Gibbs-preserving maps, one is allowed to carry out any completely positive, trace-preserving map on a system which preserves the Gibbs state at a given temperature T (or 'Gibbs-preserving map', for short). These maps are a natural quantum-mechanical generalization of the stochastic matrices used to characterize the so-called d-majorization or mixing character [21, 24–27]. Technically, these operations are convenient to work with as being a Gibbs-preserving map is a semidefinite constraint. Also, in any reasonable thermodynamical framework, a map that does not preserve the Gibbs state must cost work; this fact makes Gibbs-preserving maps a conservative choice of framework for proving fundamental limits.
Since a thermal operation preserves the Gibbs state, the state transformations possible with thermal operations are necessarily included in those achievable with Gibbs-preserving maps. Is the converse true? It is in the classical case, i.e. for states which are block diagonal in their energy eigenbasis. This can be seen as follows. A necessary and sufficient condition for transitions via thermal operations is thermo-majorization [11], a partial order which is a generalization of majorization [27–30]. More precisely, transformations are completely characterized in terms of thermo-majorization of the initial and final states' spectrum with respect to the Gibbs state. Now given the existence of a Gibbs-preserving map, classic results about majorization ensure that the initial state's eigenvalues thermo-majorize the final state's ones, meaning there exists also a thermal operation performing the transformation4 .
We now address the question of whether Gibbs-preserving maps are strictly more powerful than thermal operations, on arbitrary, quantum, input states. We show that this is the case, by exhibiting an example of a Gibbs-preserving map that performs a transformation forbidden by thermal operations.
The Example. Consider a two-level system with an energy gap 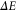 . We denote the ground state by
. We denote the ground state by 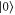 and the excited state by
and the excited state by  . Consider now the transformation:
. Consider now the transformation:
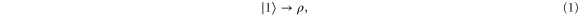
where ρ is any pure or mixed state. Depending on ρ, (in particular, in case ![$|\rho \rangle =|+\rangle \frac{1}{2}[|0\rangle +|1\rangle ]$](https://content.cld.iop.org/journals/1367-2630/17/4/043003/revision1/njp511162ieqn6.gif) as depicted in figure 1), this transformation needs to 'build' coherence between the energy levels, which, as noted above, cannot be achieved with thermal operations. We now argue that, for any
as depicted in figure 1), this transformation needs to 'build' coherence between the energy levels, which, as noted above, cannot be achieved with thermal operations. We now argue that, for any 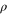 , there exists nevertheless a Gibbs-preserving map performing this transition. Let
, there exists nevertheless a Gibbs-preserving map performing this transition. Let 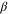 be a fixed inverse temperature, and denote the Gibbs state on the system by
be a fixed inverse temperature, and denote the Gibbs state on the system by 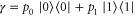 with
with 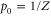 ,
, 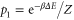 and
and 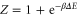 . Let Φ be defined as
. Let Φ be defined as
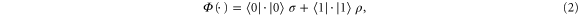
for some state 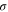 which we have not yet fixed. Note that
which we have not yet fixed. Note that 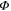 is completely positive and trace-preserving. We also have
is completely positive and trace-preserving. We also have 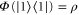 by construction. The condition that Φ be Gibbs-preserving,
by construction. The condition that Φ be Gibbs-preserving, 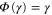 , gives us
, gives us
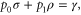
which implies
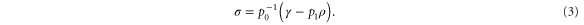
This choice of  has unit trace, and is positive semidefinite; indeed, as
has unit trace, and is positive semidefinite; indeed, as 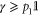 (since p1 is the smallest eigenvalue of γ) and
(since p1 is the smallest eigenvalue of γ) and 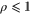 , we have
, we have 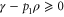 . This means that, with this choice of σ, Φ is precisely a completely positive, trace-preserving, Gibbs-preserving channel which maps
. This means that, with this choice of σ, Φ is precisely a completely positive, trace-preserving, Gibbs-preserving channel which maps  to
to 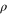 . This map is forbidden by thermal operations if
. This map is forbidden by thermal operations if 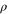 contains a coherent superposition over energy levels, and we have the desired counter-example.
contains a coherent superposition over energy levels, and we have the desired counter-example.
Figure 1. Problematic state transformation: if a qubit system is in a pure excited energy eigenstate 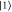 , one would expect it is possible to bring it into any other state at no work cost, in particular in the coherent superposition of energy eigenstates
, one would expect it is possible to bring it into any other state at no work cost, in particular in the coherent superposition of energy eigenstates ![$|+\rangle =\frac{1}{\sqrt{2}}[|0\rangle +|1\rangle ]$](https://content.cld.iop.org/journals/1367-2630/17/4/043003/revision1/njp511162ieqn25.gif) . This is indeed possible with Gibbs-preserving maps, however thermal operations forbid this transition because it requires nontrivial time control.
. This is indeed possible with Gibbs-preserving maps, however thermal operations forbid this transition because it requires nontrivial time control.
Download figure:
Standard image High-resolution imageThis example can easily be generalized to a system of n arbitrary energy levels: if 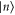 , of energy En, is such that no other state has higher energy, a Gibbs-preserving map Φ transforming
, of energy En, is such that no other state has higher energy, a Gibbs-preserving map Φ transforming 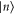 into any
into any 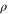 is given by
is given by
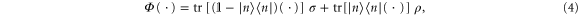
where 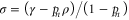 and where the Gibbs state is
and where the Gibbs state is 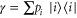 with
with 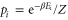 and
and 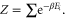
Discussion. The observation of a gap between these two classes of operations leaves open the question which of the two captures the actual physical situation. The Gibbs-preserving maps are useful as the most permissive framework that is nontrivial; there is however no known explicit microscopic model which corresponds to these operations. Furthermore, to observe any coherence between energy levels one needs a time reference frame [33–36], which might cost work to produce and eventually get degraded. Allowing the use of such a resource catalytically enables operations that were otherwise forbidden [9, 16–18], yet if the catalyst may be returned only approximately in its original state, then work can be embezzled and all transformations are possible, rendering the framework trivial [16–18]. Also, one usually expects from a physical theory that one can ignore very unlikely events; this is by definition not possible in the framework of exact catalysis. It is still an open question whether transformations achievable by Gibbs-preserving maps coincide with thermal operations combined with some form of time reference. On the other hand, if no such resource is available, additional constraints related to time covariance are required [19].
Our result, however, does not yet conclusively show that the Gibbs-preserving maps are physically irrelevant. Intuitively, one could have argued from the start that the transition equation (1) should have been possible for any 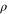 : indeed, the initial state has both maximal purity and highest possible energy. In fact, it is not uncommon to assume that some form of coherence is available, for example in the context of quantum computation, or, more generally, whenever a quantum system interacts with a macroscopic system such as a detector or a laser field; the latter are usually modelled in a coherent state.
: indeed, the initial state has both maximal purity and highest possible energy. In fact, it is not uncommon to assume that some form of coherence is available, for example in the context of quantum computation, or, more generally, whenever a quantum system interacts with a macroscopic system such as a detector or a laser field; the latter are usually modelled in a coherent state.
Finally, it is worth noting that for thermal operations, there exists a set of conditions which act as second laws, restricting which state transformations are allowed [17]. These take the form of a distance measure to the Gibbs state, and are thus also a set of restrictions for Gibbs-preserving maps (due to the data processing inequality for the Rényi relative entropies). As we now see that the two frameworks are inequivalent, this implies that a complete set of second laws will necessarily involve functions which cannot be expressed in such a form.
Acknowledgments
The authors thank Johan Åberg, Lea Krämer, David Reeb, Joe Renes, Lídia del Rio, Paul Skrzypczyk, and Stephanie Wehner for helpful discussions. PhF and RR are supported by the SNSF NCCR QSIT, the SNSF project 200020-135048, the ERC grant 258932, and the COST Action MP1209. JO thanks the EPSRC for their support. This work was in part developed during the 'Mathematical Horizons for Quantum Physics 2' program of IMS in Singapore and the 'Mathematical Challenges for Quantum Information' program of the Newton Institute in Cambridge, UK.
Footnotes
- 4
On a side note, this does not imply that Gibbs-preserving maps are equivalent to thermal operations as channels even when acting on block diagonal states. Rather, they are only equivalent in terms of state transitions. In other words, while the same pair
 can be achieved in both frameworks for block-diagonal states, the actual logical processes, i.e. trace-preserving completely positive maps or channels, that one can perform, differ. Note also that even for a given fixed input state the actual channel performed is in general relevant, and not only the input and output state, as the full information about the channel can be obtained by keeping a purification of the input [13]. Additionally, a classic example (for the trivial Hamiltonian H = 0) of a map preserving the fully mixed state but which is not a thermal operation is the Choi–Jamiolkowski map of the two-party reduced state of the Aharonov [31, note [9]] or determinant state
can be achieved in both frameworks for block-diagonal states, the actual logical processes, i.e. trace-preserving completely positive maps or channels, that one can perform, differ. Note also that even for a given fixed input state the actual channel performed is in general relevant, and not only the input and output state, as the full information about the channel can be obtained by keeping a purification of the input [13]. Additionally, a classic example (for the trivial Hamiltonian H = 0) of a map preserving the fully mixed state but which is not a thermal operation is the Choi–Jamiolkowski map of the two-party reduced state of the Aharonov [31, note [9]] or determinant state ![$|\mathcal{A}{{\rangle }_{ABC}}=\frac{1}{\sqrt{6}}[|012\rangle +|120\rangle +|201\rangle -|210\rangle -|102\rangle -|021\rangle ]$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) , which is up to a local unitary the same example as in [32].
, which is up to a local unitary the same example as in [32].





![$|\mathcal{A}{{\rangle }_{ABC}}=\frac{1}{\sqrt{6}}[|012\rangle +|120\rangle +|201\rangle -|210\rangle -|102\rangle -|021\rangle ]$](https://content.cld.iop.org/journals/1367-2630/17/4/043003/revision1/njp511162ieqn2.gif)