Abstract
We establish the path integral approach for the time-dependent heat exchange of an externally driven quantum system coupled to a thermal reservoir. We derive the relevant influence functional and present an exact formal expression for the moment generating functional which carries all statistical properties of the heat exchange process for general linear dissipation. The method is applied to the time-dependent average heat transfer in the dissipative two-state system (TSS). We show that the heat can be written as a convolution integral which involves the population and coherence correlation functions of the TSS and additional correlations due to a polarization of the reservoir. The corresponding expression can be solved in the weak-damping limit both for white noise and for quantum mechanical coloured noise. The implications of pure quantum effects are discussed. Altogether a complete description of the dynamics of the average heat transfer ranging from the classical regime down to zero temperature is achieved.

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
In recent years enormous advancements have been accomplished in the field of quantum thermodynamics both on the fundamental and practical side [1, 2]. From a fundamental perspective, a key question is how classical thermodynamics emerges from quantum dynamics [3, 4]. From a practical point of view, there is urgent need to understand how quantum systems exchange energy and heat over time [5, 6]. This is an essential step towards building new quantum devices with potentially enormous technological impact [4, 7]. To this end, the statistics of the energy supplied to and removed from a closed quantum system by a time-dependent force has been largely investigated [1, 2, 8–15].
The case in which a driven quantum system exchanges energy with a thermal reservoir is of particular interest in view of potential applications. Here the challenge is to render an adequate description of the underlying non-unitary dynamics. Because of the similarities between exchange of energy and exchange of particles, many correspondences exist between heat transfer and electron transport. The steady-state heat current between reservoirs has been studied with a Landauer-type transport formula in a nonequilibrium spin-boson model [16, 17] and in molecular junction models [18, 19]. Generalized Landauer formulae of the Meir-Wingreen type, which take also inelastic processes into account, have been applied to determine the steady-state heat current across a molecular bridge [20] and through a nano-circuit [21], and to study the Kondo effect in heat transport via a local two-state system (TSS) [22].
Heat pumping across a two-state system has been studied in weak-coupling Redfield theory [23], in the strong-coupling noninteracting-blip approximation [24], and in the Markov approximation [25]. The heat flux in a driven resonant level model has been discussed in the adiabatic regime within a scattering approach [26]. The effects of strong driving and non-Markovian dynamics on the heat flux have been studied numerically within a stochastic Liouville–von Neumann scheme [27].
By now, the full counting statistics in steady-state electron transport is well understood on the basis of Levitov–Lesovik-type formulae [28] and master equation approaches [29–31]. Much less attention has been given to heat transport. A study of the counting statistics for heat transport through a 1D harmonic chain based on the Levitov–Lesovik formula is reported in [18]. The transient behavior of the counting statistics has been investigated within nonequilibrium Green's function techniques [32]. The counting statistics of heat transfer has also been studied with master equation approaches [33, 34] and with Lindblad theory [35].
By starting out from the standard definition of heat [1, 10, 33–36], we develop a new microscopic approach to heat exchange of a general quantum system with a thermal reservoir. Our method is based on influence functional integral techniques in which all effects related to heat exchange in the reduced system are included in a specific influence functional. For any linear environment, all conceivable quantum noise sources are captured by appropriate spectral properties of the influence kernels. As in the context of dissipative quantum dynamics [37–39], the influence functional does not depend on the particular quantum system under consideration. The formalism yields, upon combining quantum coherence with random emission and absorption of energy, the full dynamics of the heat transfer process. Importantly, one can take advantage of many numerical and non-perturbative methods [40–44], as well as different well-established analytical techniques [37, 44–50], all of them available on the 'market place' of dissipative quantum mechanics.
The general formalism will be applied to the simple but non-trivial dissipative two-state or spin-boson model (SBM) [37, 51–56]. We will derive an exact formal expression for the time evolution of the average heat and heat power in the presence of an external driving field. We will show that for a constant bias the heat power can be expressed in the form of a convolution which involves the population and coherence correlation functions of the model system superimposed by polarization correlations of the heat bath accounting for heat exchange. We will present results in analytic form for weak Ohmic friction covering both the white-noise regime at high temperatures and the coloured quantum noise regime at low temperatures. The findings can potentially be tested upon using a setup similar to the one proposed in [57, 58], provided that the detector has sensitivity to resolve in real time the dynamics of the system at sufficiently low temperatures.
In section 2 we will present the microscopic model and introduce the characteristic function as the trace of a generalized density matrix of the system-plus-bath entity. In section 3 we perform the reduction of the characteristic function to the coordinates of the system alone for general coloured quantum noise and determine the respective influence functional. To investigate potential of the method, we will consider in section 4 the average heat in the dissipative TSS and we will present an exact formal expression suitable as a source for performing dynamical simulations in the presence of external driving. We will give an exact expression in analytic form for a constant bias and weak Ohmic friction which cover the entire temperature domain ranging from the classical white noise regime down to zero temperature where coloured quantum noise prevails. Finally, in section 5 we will present our conclusions.
2. Model and general settings
We consider aquantum mechanical particle of mass M, position q and momentum p moving in a time-dependent potential . We assume that the particle is coupled to a thermal bath, modelled as a set of N independent harmonic oscillators [37, 38, 51, 59]. We consider a single reservoir, but the extension to multiple reservoirs is straightforward. The Hamiltonians of the system S and reservoir R are
Here and are position and momentum of the harmonic oscillator α, respectively. The system-reservoir coupling is chosen to be bi-linear in the positions variables of system and reservoir. It reads
with the interaction strength. The second term in has been added to compensate renormalization of the potential caused by the bi-linear coupling term in [37, 38]. All effects of the reservoir on the system induced by the coupling are captured by the spectral density of the coupling
Being interested in the continuum limit , we consider smooth spectral densities of the coupling with power-law behaviour at low frequencies and spectral cut-off, e.g., exponential cutoff, at high frequencies
Here, is the coupling constant, a reference frequency and the high-frequency cut-off. The case of Ohmic damping is represented by s = 1. The regime () describes super- (sub-) Ohmic dissipation [37, 52, 55, 60]. In the sequel we consistently use units in which . Our goal is to determine the amount and the statistics of the exchanged energy between the system and the reservoir in a time interval t. This information may be obtained by performing a projective measurement of the energy of the environment both at the beginning and at the end of the time interval. Here we suppose that at initial time t = 0 the system and the bath are uncoupled, and the bath is in thermal equilibrium
where is the partition function of the reservoir. We do not specify a priori the particular form of the initial state . Importantly, different kinds of the initial preparation are feasible [37].
With the initial state (5) the Hamiltonian commutes with . Hence the measurement of the heat of the reservoir at t = 0 does not affect the dynamics. As a result, we can formulate the conditional probability for the output of the two measures and, therefore, for the dissipated heat Q [33].
The central quantity of interest, which includes the entire statistics of the heat transfer process, is the characteristic function defined as Fourier transform of the probability distribution ,
Because of the second equality, the function is referred to as the moment generating function (MGF).
The nth derivative of the MGF at gives the nth moment
The first moment, n = 1, yields the average heat transferred to the reservoir [33]. In addition, the nth cumulant of is obtained by taking the nth derivative of with respect to ν at .
A major advantage of using the MGF is that it can be written as the trace of a generalized density operator. Thus, known techniques can be applied to solve the dynamics. Following [33], we may write
where the trace is over all degrees of freedom and is the unitary evolution operator of the composite system, i.e., the corresponding generator is the total Hamiltonian .
In [33] the MGF has been studied within the weak-coupling Born–Markov approximation by solving a master equation associated with a generalized density matrix of the total system. In this work we will advance significantly by investigating the MGF from a quite different perspective. In essence, we shall derive the path integral representation of the characteristic function . This may serve as a firm basis for the study of all statistical moments of the heat transfer process, as specified in equation (7).
3. Path integral representation of the characteristic function
In this section we take the route of obtaining a closed formal expression for the characteristic function . It is advantageous to carry out the reduction of the dynamics of the system-plus-reservoir entity to the dynamics of the system alone within the functional integral description [37, 38], a technique introduced by Feynman and Vernon already in 1963 [61]. The present problem, however, is rather intricate because of the additional operator terms and in the original expression (8).
Using completeness of the position eigenstates the coordinate representation of equation (8) may be written as
The N-component vector represents the bath coordinates , and qf is the position of the particle. For convenience, the factor in equation (8) is included in the initial density matrix of the bath
The expression (9) is formally similar to the one obtained for the reduced density matrix (RDM) reported in [37] in the context of dissipative quantum dynamics. However, the substantial difference is the shifted canonical density operator and the extra factor . The latter entails independent integrations of the end/initial point and . The functional integral representation of the expression (9) reads
where is the action of the system. The double path sum represents the propagation of the RDM, while the influence functional accounts for all effects of the environmental coupling relevant to the generating function . The influence functional is found upon integrating out the bath variables in the expression (9). Details of the calculation are presented in appendix
It is convenient to rewrite the expression (11) in terms of the linear combinations
Here, q0 is a characteristic length of the system S, introduced to render the paths and dimensionless. The path , usually referred to as quasi-classical, measures propagation of the system along the diagonal of the density matrix, whereas the path measures off-diagonal excursions, i.e., quantum fluctuations. Assuming that the system is initially in a diagonal state of its density matrix, and employing the shortform the MGF then takes the form
With the results of appendix
The first factor is the familiar Feynman–Vernon influence functional represented by the actions
The local action originates from the potential counterterm in the interaction (2). The time-nonlocal action functional governs decoherence and relaxation of the reduced system [37]. The real part of is the noise action, and the imaginary part is the friction action. The former describes time-correlations of the quantum fluctuations, whereas the latter describes time-correlations between quasiclassical propagation and subsequent off-diagonal excursions. The kernel is the equilibrium time-correlation function of the collective bath mode ,
The second influence functional factor in equation (14) controls the entire statistics of the heat transport process between the system and the environment
The influence action carries in addition to the time-correlations of the aforementioned types also time-correlations between quasiclassical propagation at different time and between quantum fluctuations and subsequent quasiclassical propagation. The spectral representations of the kernels are
Evidently, coincides with the Feynman–Vernon functional at , .
The nth moment of the probability distribution is readily found from the relation (7) as
with
The energy functional in the average heat transfer is expressed in terms of the time-derivative of the equilibrium correlation function of the collective bath mode (16) as
The explicit expressions (13) and (19) for the MGF and the nth moment with the expressions (17) and (20) for and , respectively, are the main results of this section. They hold for general linear dissipation with any type of memory-friction. Evidently, the energy functional (21) carries correlations of the reduced system between different times. Increasingly more convoluted correlations appear, if we proceed to higher moments of the heat transfer process. Considering the already respectable complexity inherent in the first moment, we focus in the sequel on the discussion of the average heat and postpone discussion of statistical properties with the method proposed here to subsequent work.
We conclude this section with a short additional consideration. Firstly, we see that the term in (21) which describes time correlations between quasiclassical paths yields a contribution to even if the system is frozen in its initial position. The constant path yields the contribution
Here is the occupation probability of the initial state . Upon using the relation , where M is the inertial mass of the system, the heat portion can be directly related to the friction kernel ,
Remarkably, the heat portion (22) generally occurs when the system dynamics is slow on the scale .
Apparently, for the thermal initial state (5) of the uncoupled reservoir, the heat contribution depends on the particular initial state of the system. In fact, when the coupling is switched on at time zero, the thermal state of the uncoupled reservoir relaxes to a shifted canonical state. The initial slip (22) on the time scale represents the respective heat transfer. If we had calculated the functional for a canonical initial state with shifted oscillator positions, , and had subtracted the irrelevant constant polarization energy , the heat contribution would be
With the choice the initial slip term (24) would be absent. The relevant shifted thermal initial state can be arranged, e.g., by trapping the system at times in the particular state and releasing the constraint at time zero. Keeping this in mind, we disregard the initial slip contribution in the sequel.
4. Application to the SBM: the average heat transfer
Consider a particle moving in a double well potential and being in contact with its environment and assume that the thermal energy is small compared to the energy splitting in the individual wells. Then only the two lowest states become relevant to the dynamics. This scenario is conveniently described by the dissipative two-state or SBM. The SBM is of great interest in different fields ranging from nuclear magnetic systems to quantum optics [37, 40, 41, 51–53].
In this section we apply the method developed in the previous section to the driven SBM [37, 52, 53]. Here our interest is focused on the transferred average heat and on the heat power. The Hamiltonian of the TSS in pseudo-spin representation is
The state basis is formed by the two localized states and of the double well, which are eigenstates of with eigenvalues +1 and −1, respectively. The position operator is and has eigenvalues being associated with the minima of the double-well potential V(q). The tunneling operator transfers the particle between the two wells with tunneling amplitude Δ, while
describes an externally applied bias with a constant part , and a driving term .
4.1. Exact formal solution for the average heat
For the TSS the double path sum (13) can be visualized as a path sum for a single path that successively visits the four states of the RDM, i.e., the two diagonal or sojourn states labelled by , and the two off-diagonal or blip states labelled by . Starting out from a diagonal state of the RDM, the path dwells in sojourn j during time interval , and in a blip during time interval , where tj is the flip time. For a path with flips the initial state of the RDM is and the final state is . We choose that the RDM at initial time t = 0 is given by the populations and of the left and right well. We have and
The analysis of the path sum (19) in the SBM is reported in appendix
The integration symbol is a short form for the time-ordered integrations, equation (B.3). The bias weight of the m blips is in the factor Bm defined in equation (B.4). The factors Gm and Hm result from the noise action and from the friction action in equation (15), respectively, and they are defined in equation (B.6) with (B.7). The weight factor Gm carries the intrablip and interblip correlations of the m blips, while the weight factor Hm includes the correlations of the m sojourns with the respective subsequent blips. Finally, the double prime in indicates summation over the internal sojourn states .
From now on we restrict ourselves to the discussion of the average heat . For the piecewise constant paths (B.1) the functional (21) describes time correlations between sojourns and blips with any time-ordering. By analogy with the relation of the kernels in the actions (21) and (15), the time correlations between the - and -charges in the action are specified by the derivative of the function defined in equation (B.5). The imaginary part is connected with the damping kernel by .
Interestingly enough, the summation over the final sojourn states in the expression (28) for the first moment n = 1, by reason of the extra factor , cancels all correlations of blips and sojourns in except the correlations with the two final sojourns states. Summation of the leftover correlations yields
Here represents the correlations of sojourn k with the final sojourn m and the correlations of blip j with the final sojourn m. Explicit dependence on the end time t is indicated for later purpose. We obtain analogous to the forms (B.7) the expressions
Next, we add up the contributions of the intermediate sojourns. Further, we utilize that in equation (28) the contributions of the blip states which are odd under the substitutions cancel each other out. The resulting expression for is conveniently divided into the - and -contributions, and , and these into those which are symmetric (s) and antisymmetric (a) under bias inversion []. We readily find
where
and where . The time correlations carried by the kernel are in the functions
The expression (31) with (32) and (33) holds for linear dissipation with arbitrary memory-friction.
4.2. The Ohmic case
Of particular importance is the case of Ohmic dissipation, which is the limit in the spectral density of equation (4). In the Ohmic universality limit we have
where K is a dimensionless damping strength, . Because the kernel is memoryless, , the sojourn–sojourn correlation is restricted to the nearest-neighbour term in which the intermediate blip has length zero
Observing that a blip of zero length does not interact with other blips, the ξ-summation in equation (32) cancels all sojourn–sojourn correlations except those of the first with the second. Thus we have . In addition, the odd term is zero because the single blip left over has zero length, thus readily
Here is a dressed transition amplitude taking into account the polarization cloud of the bath modes in the adiabatic limit. We have and hence in the regime , and and hence in the regime .
Consider next the temperature-dependent term . We see from the imaginary part of the expression (34) that the blip-sojourn correlations are restricted to the nearest-neighbour term, . Thus we have . With this the expression (32) with (33) takes the form
At this point it is expedient to turn to the average heat power , which is the time derivative of the heat, . Since , the derivative of is restricted to the derivative of in equation (37). Observing that coincides with given in equation (16), we readily obtain
Equation (38) is the exact formal path sum expression for the average heat power of the TSS in the Ohmic scaling limit for any coupling strength K. Except for the last factor, the expression represents the dynamics of the RDM of the TSS under all the quantum noise-induced time-correlations carried by the functional Gm. The residual factor correlates the flip times of the TSS with the final time t. This factor is specific to the mean of the heat power. The expression (38) may be used to calculate the time dependence of the heat power for any time-dependent driving of the system according to equation (26).
To sound out validity and potential of the presented method, we now study the expression (38) for a constant bias . First, we see that in the term of the blip , which may take any position in the sequence of m blips, plays a particular role. In the weak damping limit, we may safely disregard the interblip correlations of the preceding and the subsequent blips with the blip ℓ, and , as well as all interblip correlations across this blip, i.e., , where and . Then the series (38) can be expressed in terms of a convolution which involves in the time segment the population correlation function [51] and the coherence correlation function of the TSS [37, 62, 63]. The resulting expression is
Here the index s (a) indicates that the respective term is symmetric (antisymmetric) under bias inversion, . The initial conditions are and .
In the further analysis of the average heat power we can thus employ known analytic results for the nonequilibrium correlation functions and reported in the recent literature [37, 51, 60].
To conclude this subsection, we consider as a preparatory work for the subsequent studies the total heat transferred from the TSS to the reservoir in the weak damping regime. Writing the localized states and as linear combinations of the ground state and excited state of , and assuming initial preparation according to equation (27) and thermal occupation of the states and at time infinity, we obtain
where and indicate the initial and equilibrium energy of the system respectively. In the following subsections, we shall apply these results to study the heat transfer for weak damping in the Markov and in the quantum noise regime.
4.3. Markov regime
In the temperature regime , the power spectrum of the collective bath mode is essentially white, , where . Then the real parts of the polarization correlation function and the flip-pair correlation function of equation (34) take the form and . Here is the adiabatic contribution which dresses the transfer matrix element according to .
Observing that the function is memory-less and the initial conditions for and in equation (39) are and , the expression (39) for the heat power reduces to the concise form
Since the pair interaction , the interblip correlations are zero. As a result, the series for the coherence correlation function is easily summed in Laplace space, yielding [37, 63]
Importantly, the residuum of the pole at the origin, which is the equilibrium value of reached at time infinity, together with the factor cancels exactly the constant term in equation (41). This secures that the heat power in fact vanishes as , and the dynamics of is determined by the simple zeros , and of the denominator in equation (42). The resulting expression is
where 'cycl.' denotes addition of the terms obtained by cyclic permutation of the indices. The behaviours of , and reflect the characteristics of a cubic equation with real coefficients, which depend on δ,  and the scaled temperature ϑ. Physically, it is natural to write them in terms of an oscillation frequency Ω, a decoherence rate γ and a relaxation rate as and .
and the scaled temperature ϑ. Physically, it is natural to write them in terms of an oscillation frequency Ω, a decoherence rate γ and a relaxation rate as and .
In the temperature regime the bath coupling is a perturbation. In the leading one-boson exchange approximation, the rates increase linearly with the scaled temperature ϑ,
As temperature is raised, multi-boson exchange processes become increasingly important. In the temperature range well above , the decoherence and relaxation rates show drastically different behaviours
In this so-called Kondo regime, the relaxation rate decreases with increasing temperature as , whereas the decoherence rate increases linearly with T.
Integration of the expression (43) yields the average heat transferred to the reservoir until time t. Readily the average heat transferred until time infinity is found from equation (43) in the Markovian regime as
It is straightforward to see by use of the Vieta relations for the frequencies , and , that the expression (46) holds for all T in the Markov regime. Importantly, the result (46) is just the high-temperature limit of the expression (40).
4.4. Quantum noise regime
For temperatures of the order or lower, the power spectrum is coloured because of quantum mechanical noise and the functions and carry memory. Nevertheless, it is possible to calculate exactly the one-boson contribution to the rates γ and [37, 60]. The resulting expressions are
where and . The correlation functions and going down into the expression of equation (39) take the form
Next, the convolution in equation (39) is conveniently evaluated by using for its spectral representation in equation (16) and writing the -function in terms of the sum representation
where is a bosonic Matsubara frequency. Then the τ-integration is straightforward. The remaining ω-integral picks up (i) a contribution from the singularity at formed in the limit and (ii) a contribution from the residua of the infinite sequence of poles stringed along the imaginary axis at . This split-up into a system and a Matsubara part is a general feature of equilibrium correlation functions in the quantum regime.
The first contribution has a part which cancels the first term in equation (39), and the remaining part is
The contribution from the Matsubara poles is odd in the bias and is
where
These functions can be written as linear combinations of hypergeometric -functions which reduce to sine and cosine integral functions at T = 0. The function depends logarithmically on the cutoff .
As the Markov regime at T well above Ω is approached, the expression (50) smoothly matches on the expression (43) with the one-boson rates (44). The heat power term is a pure quantum contribution, which is negligibly small in this regime. Conversely, as the temperature is lowered, quantum effects appear in through the coth-function in the amplitude and in the rate expressions (47). This function indicates emission and absorption of quanta with energy ω in thermal equilibrium. Moreover, the term becomes increasingly important as T is decreased, and may even dominate the time-dependence of the heat power at low T. The combined expression can be conveniently written in terms of the amplitudes
With these forms, the antisymmetric part of the total average heat power is conveniently written in terms of the amplitude of the relaxation contribution, the amplitude of the oscillatory contribution, and a phase shift ,
The resulting expression for the total mean heat power is
The oscillatory part of describes seesaw transport of heat between system and reservoir. The damped oscillatory parts are superimposed by relaxation contributions.
Considering equation (55) and comparing it with equation (50), one can deduce that the degree of deviation from unity of the amplitude factors and indicate the relative strength of the pure quantum contribution . Indeed, in the case and one recovers the form (50) in which the pure quantum contribution is absent. The amplitudes and , and the phase are plotted in figures 1 and 2 as a functions of time for three different temperatures. The amplitude approaches unity in the regime for and in the regime for . For fixed T, the amplitude is monotonically decreasing as time t is lowered and eventually changes sign at time t0. In the temperature regime , the instant t0 depends inversely on T as and eventually enters the core region, at temperatures of the order . Reversely, the instant t0 increases with decreasing temperature and reaches at T = 0 the maximal value .
Figure 1. The amplitudes and are plotted versus time for different temperatures, T = 0.1 (black solid), T = 1 (blue dashed), and T = 3 (red dotted). The parameters are , , and K = 0.02. Times, frequencies and temperature are scaled with δ. The time where changes sign and the time where it approaches unity move towards the origin as temperature is increased. Correspondingly, the minimum of moves to the origin, as T is increased. Other characteristics of and are discussed in the main text.
Download figure:
Standard image High-resolution imageFigure 2. The phase φ is plotted as a function of time for different temperatures, T = 0.1 (black solid), T = 1 (blue dashed), and T = 3 (red dotted). The other parameters are the same as in figure 1. The phase jump by π occurs at the instant where the amplitude changes sign. The constant value at asymptotic times increases with decreasing temperature.
Download figure:
Standard image High-resolution imageThe amplitude has a minimum at the time t0, at which is zero, whereas the phase undergoes a sudden jump from to as t passes t0 from below. At times below t0, the pure quantum contribution dominates the behaviour of the heat power . Both the amplitudes and the phase approach constant values and at times . These values get larger as T is decreased, and at low T they are notably different from the values and holding in the absence of the pure quantum contribution . The asymptotic values are largest at T = 0 and are
where , and where is Euler's constant. This shows that the direct time dependence of and at low T strongly depends on the pure quantum contribution for all times. These non-Markovian effects could be measured at temperature , provided that the detector used can resolve the signal with the sufficient accuracy for time .
On the bottom line, the contribution of to the overall heat is negligibly small. In the asymptotic weak-damping limit, the total heat transferred to the bath is found from the expression (55) as
With the form (47) for , coincides with the expression (40).
Plots of and are shown for different temperatures and different initial conditions in figures 3 and 4. The oscillations of are clearly visible for the case both for initial condition in panel (a) and for in panel (b). For , the three curves stay together until time and then diverge to reach the respective asymptotic values indicated by the arrows on the right border. We see from the curves in figure 4 (b), which correspond to the initial condition , that the heat can be positive or negative, dependent on temperature.
Figure 3. The mean heat power (in units of ) is plotted as a function of time for different temperatures, T = 0.1 (black solid), T = 1 (blue dashed), and T = 3 (red dotted). The parameters are , , and K = 0.02. Times, frequencies and temperature are scaled with δ. The initial condition is in panel (a) and in panel (b). The phases of the oscillations in panel (b) differ from the corresponding ones in panel (a) by π. The quality of the oscillations decreases with increasing T.
Download figure:
Standard image High-resolution imageFigure 4. The mean heat (in units of δ) is plotted as a function of time for different temperatures, T = 0.1 (black solid), T = 1 (blue dashed), and T = 3 (red dotted). The parameters are , , and K = 0.02. Times, frequencies and temperature are scaled with δ. The initial condition is in panel (a) and in panel (b). The phases of the oscillations in panel (b) differ from the corresponding ones in panel (a) by π. The quality of the oscillations decreases with increasing T. The respective total heat transferred, which is calculated from the expression (40), is indicated by the arrow at the right border.
Download figure:
Standard image High-resolution image5. Conclusions
In this paper we established the functional integral description for the time-dependent heat exchange of a quantum system coupled to a thermal reservoir. We presented the exact formal solution for the moment generating functional which carries all statistical features of the heat exchange process for general linear dissipation. We derived an exact formal expression for the transferred heat and applied this formalism to the dissipative TSS. We showed that the difference between the dynamics of the heat transfer and the dynamics of the RDM is an additional time-nonlocal correlation function which correlates intermediate states of the RDM with the final state.
To investigate the potential of the presented method, we calculated the dynamics of the average heat power and average heat in analytic form for weak Ohmic dissipation both in the Markovian regime relevant at high temperatures and in the non-Markovian quantum noise regime holding when temperature is of the order of the level splitting Ω or lower. In the latter regime, the heat is represented by a convolution integral which involves the population and coherence correlation functions of the dissipative TSS and the polarization correlation function of the reservoir. We find that the heat transfer receives contributions both from singularities related to the system dynamics and from Matsubara singularities resulting from the system-reservoir correlations. The latter yield significant contributions in the quantum noise regime while they are absent in the Markovian regime.
Altogether we have achieved a complete description of the dynamics of the heat transfer for weak damping ranging from the classical regime down to zero temperature.
Acknowledgments
We acknowledge the support of the MIUR-FIRB2012—Project HybridNanoDev (Grant No.RBFR1236VV), EU FP7/2007—2013 under REA grant agreement no 630925—COHEAT, MIUR-FIRB2013—Project Coca (Grant No. RBFR1379UX), and the COST Action MP1209. UW acknowleges support from the Deutsche Forschungsgemeinschaft through SFB/TRR21.
Appendix A.: Influence functional
In this appendix we outline the evaluation of the influence functional . Here we use the inverse temperature , but return to T when we employ the expressions (A.17) in section 3.
Upon comparing the expressions (9) and (11) the influence functional is found to be defined as
Here the amplitude
is the propagator of the bath exposed to the system-bath coupling, .
At first, we see that the influence functional can be written in the product form
The term is the contribution of the bath oscillator α. Dropping the redundant label R we have
The matrices of the density operators and depend solely on coordinates of the bath oscillator α and may be written as
The prefactor and the Euclidean action for an imaginary-time interval τ are given by
and is the partition function of the reservoir mode α.
Correspondingly, the propagator of the driven oscillator α takes the form
The phase is determined by the real-time action in the presence of the external force [37, 61]
where
The first term in equation (A.8) is the phase resulting from the internal oscillator dynamics, the second and third terms depend linearly on the initial and final oscillator position and on the history of the system. Finally, is a global phase which does not depend on the reservoir mode
where . Here the first term originates from the counter term in the interaction given in equation (2). We can thus write the generalized influence functional in the form
where captures the integrations of the bath mode α,
The exponent of the integrand of the fourfold integral (A.12) is a Gaussian form. Written in terms of the symmetric and antisymmetric cordinates and , the Gaussian form is free of mixed terms . Hence both the - and the -integrations may be performed by completing the square
With the shift the arising quadratic form of the exponent is free of the mixed term . Thus the remaining - and -integrals can be done by using again twice the relation (A.13). The various pre-exponential factors that accrued multiply to unity. In addition, the arising exponent is conveniently expressed in terms of the paths and given in equation (12). After all, the resulting expression for the influence functional (A.4) may be written in the form
with
The kernels are
Appendix B.: Path sum in the SBM
Here we sketch the derivation of the expression (28). First, the piecewise constant paths with flips are
where and . Here the initial state of the RDM is and the final state is .
The path sums in equations (13) and (19) result in a series in the number of flip pairs, and in each term the summation of all possible arrangements in the time-ordered alternating series of sojourns and blips
The weight to switch per unit time from the diagonal state to the directly following off-diagonal state is , and the weight to switch per unit time from the offdiagonal state to the directly following diagonal state is . Thus, the aggregated weight of flips depends only on the initial and final sojourn state and is . The weight to stay in a sojourn is unity, whereas the weight to stay in the blip during time interval is . Accordingly, the contributions of m blips are accumulated in the bias weight factor
For the piecewise constant path (B.1) in the influence action the time correlations among the - and - labels or charges are expressed in terms of the second integral of the function ,
The resulting correlation factor for flips is , where [52, 62, 63]
and where
Here we used the short form . The functions and describe the interactions between blip k and subsequent blip j, and the interactions between sojourn k and subsequent blip j, respectively. With these individual terms the moment takes the form given in equation (28).












































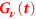














![${{S}_{{\rm S}}}[q]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn45.gif)
![${{\mathcal{F}}^{(\nu )}}[q,q^{\prime} ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn46.gif)

![${{\mathcal{F}}^{(\nu )}}[q,q^{\prime} ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn48.gif)





![${{S}_{{\rm S}}}[\eta ,\xi ]={{S}_{{\rm S}}}[q]-{{S}_{{\rm S}}}[q^{\prime} ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn53.gif)



![$\Phi _{{\rm loc}}^{(0)}[\eta ,\xi ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn54.gif)
![$\Phi _{{\rm cor}}^{(0)}[\eta ,\xi ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn55.gif)
![$\Phi _{{\rm cor}}^{(0)}[\eta ,\xi ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn56.gif)



![${{{\rm e}}^{{\rm i}\Delta {{\Phi }^{(\nu )}}[\eta ,\xi ]}}$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn59.gif)

![$\Delta {{\Phi }^{(\nu )}}[\eta ,\xi ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn60.gif)

![${{\mathcal{F}}^{(\nu )}}[q,q^{\prime} ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn61.gif)

![${{\mathcal{F}}^{(0)}}[q,q^{\prime} ]={{\mathcal{F}}_{{\rm FV}}}[q,q^{\prime} ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn63.gif)



![${{\Phi }^{(1)}}[\eta ,\xi ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn65.gif)





![$\Delta {{\Phi }^{(\nu )}}[\eta ,\xi ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn70.gif)
![${{\Phi }^{(n)}}[\eta ,\xi ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn71.gif)












![${{H}_{{\rm I}}}[{{\eta }_{i}}{{q}_{0}}/2,{\boldsymbol{x}} ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn82.gif)

![${{\Phi }^{(1)}}[\eta ,\xi ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn84.gif)




































![${{\Phi }^{(1)}}[{{\eta }^{(m)}},{{\xi }^{(m)}}]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn116.gif)







































![${{W}_{{\rm adia}}}=2K{\rm ln} [{{\omega }_{{\rm c}}}/(2\pi T)]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn148.gif)



















































![${{W}_{{\rm adia}}}=2K{\rm ln} [{{\omega }_{{\rm c}}}/(2\pi T)]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn196.gif)

























































































































![${{B}_{\infty }}=(2/\pi )[\;{\rm ln} ({{\omega }_{{\rm c}}}/\Omega )-{{C}_{{\rm E}}}]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn300.gif)

































![${{\mathcal{F}}^{(\nu )}}[q,q^{\prime} ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn331.gif)

![${{\mathcal{F}}^{(\nu )}}[q,q^{\prime} ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn333.gif)


![${{S}_{{\rm I}}}[q,{\boldsymbol{x}} ]=-\int {\rm d}\tau {{H}_{{\rm I}}}[q,{\boldsymbol{x}} ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn334.gif)
![${{\mathcal{F}}^{(\nu )}}[q,q^{\prime} ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn335.gif)

![$\mathcal{F}_{\alpha }^{(\nu )}[q,q^{\prime} ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn336.gif)







![${{Z}_{\alpha }}=1/[2{\rm sinh} (\beta {{\omega }_{\alpha }}/2)]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn341.gif)




![${{\psi }_{\alpha }}[q]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn343.gif)



![${{\mathcal{F}}^{(\nu )}}[q,q^{\prime} ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn346.gif)





































![${\rm exp} [\;{\rm i}\;{{\xi }_{j}}\int _{{{t}_{2j-1}}}^{{{t}_{2j}}}{\rm d}t^{\prime} \epsilon (t^{\prime} )]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn374.gif)

![$\Phi _{{\rm cor}}^{(0)}[\eta ,\xi ]$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn375.gif)





![${{({{{\rm e}}^{-\Phi _{{\rm cor}}^{(0)}[\eta ,\xi ]}})}_{m}}={{G}_{m}}\;{{H}_{m}}$](https://content.cld.iop.org/journals/1367-2630/17/4/045030/revision1/njp512448ieqn380.gif)





