Accurate localized resolution of identity approach for linear-scaling hybrid density functionals and for many-body perturbation theory

The nonlocal exchange operator as part of the generalized Kohn–Sham or Fock matrix is defined by

$$\begin{eqnarray}&&{K}_{{il}}:= \displaystyle \sum _{{jk}}{D}_{{jk}}({ij}| {kl}),\end{eqnarray} \tag{ 2 }$$

where D_jk is the one-particle density matrix and $({ij}| {kl})$ are four-center integrals of basis functions ${\varphi }_{i}({\bf{r}})$, analogous to the four-center integrals defined in equation (1) for the orbitals ${\psi }_{s}({\bf{r}})$.

In the RI, orbital products ${\varphi }_{i}({\bf{r}}){\varphi }_{j}({\bf{r}})=:{\rho }_{{ij}}({\bf{r}})$ are expanded in a set of auxiliary basis functions ${P}_{\mu }({\bf{r}})$:

$$\begin{eqnarray}&&{\rho }_{{ij}}({\bf{r}})\approx \displaystyle \sum _{\mu }{C}_{{ij}}^{\mu }{P}_{\mu }({\bf{r}})\;=:\;{\tilde{\rho }}_{{ij}}({\bf{r}})\end{eqnarray} \tag{ 3 }$$

to give the approximated product ${\tilde{\rho }}_{{ij}}({\bf{r}})$. The two-electron integrals (equation (1)) are then reduced to:

$$\begin{eqnarray}({ij}| {kl}) & = & \displaystyle \sum _{\mu ,\nu }{C}_{{ij}}^{\mu }{V}_{\mu \nu }{C}_{{kl}}^{\nu },\\ {V}_{\mu \nu } & = & ({P}_{\mu }| {P}_{\nu }).\end{eqnarray} \tag{ 4 }$$

Several strategies have been proposed to determine the expansion coefficients ${C}_{{ij}}^{\mu }$. The most common variant is known as 'RI-V'. This approach directly minimizes the error of the four-center integrals. Whitten has shown [24] that this can be achieved by minimizing the Coulomb integral of the fitting error $(\delta {\rho }_{{ij}}| \delta {\rho }_{{ij}})$:

$$\begin{eqnarray*}\delta {\rho }_{{ij}}({\bf{r}}) & = & {\rho }_{{ij}}({\bf{r}})-{\tilde{\rho }}_{{ij}}({\bf{r}}),\\ & = & {\varphi }_{i}({\bf{r}}){\varphi }_{j}({\bf{r}})-\displaystyle \sum _{\mu }{C}_{{ij}}^{\mu }{P}_{\mu }({\bf{r}}).\end{eqnarray*}$$

The minimization problem then leads to a system of linear equations:

$$\begin{eqnarray}&&0\overset{!}{=}\displaystyle \frac{1}{2}\displaystyle \frac{\partial (\delta {\rho }_{{ij}}| \delta {\rho }_{{ij}})}{\partial {C}_{{ij}}^{\mu }}=\displaystyle \sum _{\nu }(\mu | \nu ){C}_{{ij}}^{\nu }-(\mu | {ij})\end{eqnarray} \tag{ 5 }$$

yielding the expansion coefficients and the approximated four-center integrals:

$$\begin{eqnarray}&&{C}_{{ij}}^{\mu }=\displaystyle \sum _{\nu }({ij}| \nu ){V}_{\nu \mu }^{-1}\end{eqnarray} \tag{ 6 }$$

$$\begin{eqnarray}&&\Rightarrow \;({ij}| {kl})\approx \displaystyle \sum _{\mu ,\nu }({ij}| \mu ){V}_{\mu \nu }^{-1}(\nu | {kl}).\end{eqnarray} \tag{ 7 }$$

The four-index matrix we started with is now represented by only two- and three-index objects, implying a significant advantage in terms of memory requirements and computational time. Furthermore, the error of the approximated four-center integrals is quadratic in the residual $\delta {\rho }_{{ij}}({\bf{r}})={\rho }_{{ij}}({\bf{r}})-{\tilde{\rho }}_{{ij}}({\bf{r}})$ of the fitted orbital product [25].

Unfortunately, the Coulomb kernel $v({\bf{r}}-{\bf{r}}^{\prime} )$ is long-ranged, so that $(\mu | \nu )$ and $(\mu | {ij})$ are neither sparse nor short-ranged except when the overlap between ${\varphi }_{i}$ and ${\varphi }_{j}$ vanishes. The consequence is a canonical $O({N}^{3})$ computational and memory scaling with system size for the precomputed expansion coefficients ${C}_{{ij}}^{\mu }$. It can be reduced to $O({N}^{2})$ memory scaling by taking the vanishing overlaps into account, but in both cases there is a large prefactor in actual computations. The formal $O({N}^{4})$ scaling for the exchange matrix construction is not reduced by the RI approach, unless density matrix screening techniques [55] are used when the exchange matrix is computed. Since the Coulomb metric distributes the expansion coefficients ${C}_{{ij}}^{\mu }$ for any given (localized) density ${\rho }_{{ij}}({\bf{r}})$ over all auxiliary basis functions ${P}_{\mu }({\bf{r}})$ in the system, O(N) scaling can no longer be achieved for the exchange operator.

In our implementation [16, 32], all atom-centered basis functions ${\varphi }_{i}({\bf{r}})$ are defined as:

$$\begin{eqnarray}&&{\varphi }_{i}({\bf{r}})={u}_{{skl}}(r){Y}_{{lm}}(\phi ,\theta ),\end{eqnarray} \tag{ 8 }$$

where u_skl(r) is a radial function with index k and angular momentum l for species s and ${Y}_{{lm}}(\phi ,\theta )$ denotes a spherical harmonic. Both the radial part and the spherical harmonics are real-valued functions. The basis functions are constructed numerically and are subject to a cut-off potential V_cut(r), which enforces a smooth decay to zero of the basis functions outside the relevant range [16]. The construction of the confined basis functions is described in detail in equations (8) and (9) of [16]. In short, all radial functions in FHI-aims are solutions to:

$$\begin{eqnarray}&&\left[-\displaystyle \frac{1}{2}\displaystyle \frac{{{\rm{d}}}^{2}}{{\rm{d}}{r}^{2}}+\displaystyle \frac{l(l+1)}{{r}^{2}}+{V}_{i}(r)+{V}_{\mathrm{cut}}(r)\right]{u}_{i}(r)={\epsilon }_{i}{u}_{i}(r).\end{eqnarray} \tag{ 9 }$$

Our auxiliary basis functions ${P}_{\mu }({\bf{r}})$ are not predefined, but rather derived from the basis set $\{{\varphi }_{i}({\bf{r}})\}$ used to expand the orbitals $\psi ({\bf{r}})$. Our construction scheme for the ${P}_{\mu }({\bf{r}})$ ensures an exact reproduction of those integrals $({ij}| {kl})$ with basis functions $i,j,k,l$ centered at the same atom, which account for the major part of the total energy. We therefore construct our auxiliary basis set such that it contains all on-site products of basis functions ${\varphi }_{i}({\bf{r}})\cdot {\varphi }_{j}({\bf{r}})$ explicitly. Specifically, the auxiliary basis set can be derived from two different underlying basis sets:

• OBS: the standard orbital basis set used to expand the Kohn–Sham orbitals of the DFT calculation
• OBS+: an enhanced OBS with additional functions, which are used only for the construction of the ${P}_{\mu }({\bf{r}})$ functions

In figure 1 the auxiliary basis construction is illustrated as a flowchart. For each atom species s in the system we compute all on-site products ${u}_{{{sk}}_{1}{l}_{1}}(r){u}_{{{sk}}_{2}{l}_{2}}(r)$ of the radial basis functions u_skl(r). These products are then orthogonalized with a Gram–Schmidt scheme. A radial product is accepted as a new radial auxiliary basis function in a given angular momentum channel if the norm of its projection orthogonal to the already accepted functions is larger than a small value ${\epsilon }_{\mathrm{orth}}$ (for RI-V: 10⁻² for atoms with $Z\leqslant 10$, 10⁻³ for atoms with $10\leqslant Z\leqslant 18$ and 10⁻⁴ for all other elements).

Zoom In Zoom Out Reset image size

The choice of this parameter controls the size of the auxiliary basis $\{{P}_{\mu }({\bf{r}})\}$ and thus the expansion accuracy [32]. The accepted products are then multiplied with each spherical harmonic ${Y}_{{lm}}(\phi ,\theta )$ which satisfies the Clebsch–Gordon condition $| {l}_{1}-{l}_{2}| \leqslant l\leqslant | {l}_{1}+{l}_{2}|$ to obtain the ${P}_{\mu }({\bf{r}})$. The maximum angular momentum of any basis function in the OBS or OBS+ of a given species, l_s^max, thus also controls the maximum angular momentum of any basis function in the auxiliary basis set, $2{l}_{s}^{\mathrm{max}}$. For each species s the maximal angular momentum of the product functions ${l}_{{\rm{s}}}^{\mathrm{cap}}$ can be capped to reduce the size of the auxiliary basis, but this comes at the price of a reduced accuracy. In this work, we do not restrict l_s^cap in any way for either RI-V or for our new localized RI. For production calculations beyond this work, we find that l_s^cap should never be reduced for the localized RI. For RI-V, we find that l_s^cap = 5 for elements below Xe (Z = 54) and l_s^cap = 6 for heavier elements are sufficient for well-converged results.

Our standard procedure for the construction of the $\{{P}_{\mu }({\bf{r}})\}$ has the advantage of producing an atom-centered auxiliary basis that automatically adapts itself to the orbital basis set and that yields a particular high accuracy for on-site products. The off-site products on the other hand are not included in the auxiliary basis set and therefore will not be expanded exactly. To obtain accurate results for these integrals too, we must use a sufficiently large auxiliary basis set. This can be readily achieved with our construction scheme by enhancing the OBS with additional functions, which are used only for the construction of the auxiliary basis set, as shown by the gray box in figure 1. This enhanced OBS is labeled OBS+ and yields a larger set of $\{{P}_{\mu }({\bf{r}})\}$ functions. Since the auxiliary basis is constructed at the species level, this approach will add the additional auxiliary basis functions to each atom of the affected species. The choice of additional basis functions will be discussed in detail in section 3.1.

As our aim in this work is to reduce the number of expansion coefficients substantially, we restrict the expansion coefficients ${C}_{{ij}}^{\mu }$ to be non-zero only if the auxiliary function μ is centered at one of the two atoms at which the basis functions i and j are centered. This restricted expansion of the product ${\varphi }_{i}({\bf{r}}){\varphi }_{j}({\bf{r}})$ (centered on atoms I and J) can be written as

$$\begin{eqnarray}&&{\tilde{\rho }}_{{ij}}({\bf{r}})=\displaystyle \sum _{\mu \in {\mathcal{P}}({IJ})}{C}_{{ij}}^{\mu }{P}_{\mu }({\bf{r}})\end{eqnarray} \tag{ 10 }$$

where ${\mathcal{P}}({IJ}):= {\mathcal{P}}(I)\cup {\mathcal{P}}(J)$ denotes the set of all auxiliary functions centered at atom I or atom J, as depicted in figure 2.

Zoom In Zoom Out Reset image size

Since the RI-V prescription has proven to be a robust scheme, we use the same minimization target for our localized variant. In practice, this means that we minimize the Coulomb self-repulsion $(\delta {\rho }_{{ij}}| \delta {\rho }_{{ij}})$ of the residual $\delta {\rho }_{{ij}}({\bf{r}})$ from the restricted expansion:

$$\begin{eqnarray*}\delta {\rho }_{{ij}}({\bf{r}}) & = & {\rho }_{{ij}}({\bf{r}})-{\tilde{\rho }}_{{ij}}({\bf{r}})\\ & = & {\varphi }_{i}({\bf{r}}){\varphi }_{j}({\bf{r}})-\displaystyle \sum _{\mu \in {\mathcal{P}}({IJ})}{C}_{{ij}}^{\mu }{P}_{\mu }({\bf{r}})\end{eqnarray*}$$

with respect to variations in ${C}_{{ij}}^{\mu }$. The minimization condition then leads to a set of linear equations similar to the one for RI-V (equation (5)):

$$\begin{eqnarray}&&0\overset{!}{=}\displaystyle \frac{1}{2}\displaystyle \frac{(\delta {\rho }_{{ij}}| \delta {\rho }_{{ij}})}{{C}_{{ij}}^{\mu }}=\displaystyle \sum _{\nu }^{{\mathcal{P}}({IJ})}(\mu | \nu ){C}_{{ij}}^{\nu }-(\mu | {ij})\end{eqnarray} \tag{ 11 }$$

for the coefficients ${C}_{{ij}}^{\nu }$. Both indices μ and ν are restricted to the subset ${\mathcal{P}}({IJ})$. As a consequence, the system of linear equations can be decomposed into a set of subproblems, one for each atom pair. Finally, the expansion coefficients and four-center integrals can be written as

$$\begin{eqnarray}{C}_{{ij}}^{\nu }=\left\{\begin{array}{ll}\displaystyle \sum _{\mu \in {\mathcal{P}}({IJ})}{L}_{\nu \mu }^{{IJ}}\;(\mu | {ij}) & \nu \in {\mathcal{P}}({IJ})\\ 0 & \mathrm{else}\end{array}\right.\end{eqnarray} \tag{ 12 }$$

with ${{\bf{L}}}^{{IJ}}={({{\bf{V}}}^{{IJ}})}^{-1}$ where ${{\bf{V}}}^{{IJ}}$ is a square matrix with the entries $(\mu | \nu )$ for $\mu ,\nu \in {\mathcal{P}}({IJ})$. The dimension of ${{\bf{L}}}^{{IJ}}$ is therefore ${N}_{{aux}}^{{IJ}}\times {N}_{{aux}}^{{IJ}}$ with N_aux^IJ being the number of $\{{P}_{\mu }({\bf{r}})\}$ centered on atoms I and J, which is only a small fraction of the total number of auxiliary basis functions N_aux. If we now insert equation (12) into equation (4), we obtain

$$\begin{eqnarray}&&\Rightarrow ({ij}| {kl})\approx \displaystyle \sum _{\underset{\nu \sigma \in {\mathcal{P}}({KL})}{\mu \lambda \in {\mathcal{P}}({IJ})}}({ij}| \lambda ){L}_{\lambda \mu }^{{IJ}}{V}_{\mu \nu }{L}_{\nu \sigma }^{{KL}}(\sigma | {kl})\end{eqnarray} \tag{ 13 }$$

where the sums are restricted to the subset ${\mathcal{P}}({IJ})$ because of equation (12). We name this expansion 'RI-LVL' after the matrices occurring in equation (13).

One advantage of this scheme lies in the fact that the size of the local Coulomb matrices ${{\bf{V}}}^{{IJ}}$ required for each atom pair is independent of the system size. Their number initially increases quadratically, but with increasing system size the number of relevant pairs scales linearly. Due to the cubic scaling of matrix inversions, the inversion of several local Coulomb matrices becomes favorable for large systems compared to the single inversion of a global Coulomb matrix.

Furthermore, we no longer need the full three index object $({ij}| \mu )$, but only the parts relevant for equation (12). Additionally, the calculation of the remaining three-index integrals $({ij}| \mu )$ is simplified within RI-LVL because the center of μ is either I or J. The product of the Coulomb potential of ${P}_{\mu }$ with, say, ${\varphi }_{i}$ is a simple superposition of atom-centered functions, whose overlap with ${\varphi }_{j}$ can be calculated in Fourier space using the methods suggested by Talman [43, 46] as described in [32]. Together with the strong reduction in the number of these integrals the computational time can be reduced to an extent where it is small compared to the other parts of the calculation.

The following exact relation of four-center integrals and their RI approximations

$$\begin{eqnarray}({ik}| {jl}) & = & ({\tilde{\rho }}_{{ik}}| {\tilde{\rho }}_{{jl}})+({\tilde{\rho }}_{{ik}}| \delta {\rho }_{{jl}})+(\delta {\rho }_{{ik}}| {\tilde{\rho }}_{{jl}})+(\delta {\rho }_{{ik}}| \delta {\rho }_{{jl}})\end{eqnarray} \tag{ 14 }$$

is important for assessing the accuracy of RI schemes. Here, ${\rho }_{{ik}}({\bf{r}})={\varphi }_{i}({\bf{r}}){\varphi }_{k}({\bf{r}})$ are the exact products, ${\tilde{\rho }}_{{ik}}({\bf{r}})$ their RI approximations and $\delta {\rho }_{{ik}}({\bf{r}})={\rho }_{{ik}}({\bf{r}})-{\tilde{\rho }}_{{ik}}({\bf{r}})$ are the residuals. The first term is the straightforward RI expansion used so far. The next two terms are linear in the residual, whereas the last is quadratic in the residual.

In RI-V, the minimization criterion for the residual equation (5) can be rewritten as $0=(\mu | \delta {\rho }_{{ik}})$. Since all approximated products $\tilde{\rho }({\bf{r}})$ are expanded in the $\{{P}_{\mu }({\bf{r}})\}$, the linear terms must vanish in RI-V.

The localized version, on the other hand, only enforces this condition for those $\{{P}_{\mu }({\bf{r}})\}$ which are centered on the same atoms as the basis function composing the product. Therefore, the linear terms will only vanish for those integrals for which $\{I,K\}=\{J,L\}$, where the capital letters denote the atom index of the corresponding orbital basis function. For all other integrals, the error is linear in the residuals.

Some localized RI-schemes alleviate this error by using the robust Dunlap correction[25]. Localized schemes can be extended to yield quadratic errors in the residual by including the linear error terms from equation (14) in (13):

$$\begin{eqnarray}&&(\tilde{{ik}| {jl}})=({\tilde{\rho }}_{{ik}}| {\rho }_{{jl}})+({\rho }_{{ik}}| {\tilde{\rho }}_{{jl}})-({\tilde{\rho }}_{{ik}}| {\tilde{\rho }}_{{jl}}).\end{eqnarray} \tag{ 15 }$$

In RI-V, all of these three terms are identical and therefore reduce to the previously used formula (equation (7)) for the four-center integral. This expression has a few drawbacks: to calculate the correction terms, all of the three-index Coulomb integrals $(\mu | {jl})$ are required. (This also includes those for which ${P}_{\mu }({\bf{r}})$ is not centered on the same atom as ${\varphi }_{j}({\bf{r}})$ or ${\varphi }_{l}({\bf{r}})$.) Since the sparsity in the three-index Coulomb integrals is the key to our memory and computational time savings, this correction would undo most of our achievements. Furthermore, it also has been recently demonstrated [40] that this expression can lead to serious convergence problems in rare cases, because the matrix for the approximated four-center integrals is not necessarily positive semi-definite. Since negative eigenvalues correspond to attractive electron–electron interactions, the usual safeguards to ensure SCF convergence will lead to a high ratio of rejected steps, slowing SCF convergence down or preventing convergence at all.

Due to these drawbacks, we do not employ the Dunlap correction for our localized scheme. As we will show in section 3, the combination of a localized RI from equation (13) with localized NAOs nevertheless reproduces the results obtained from RI-V with essentially exact accuracy while significantly decreasing the computational requirements. The key step is an appropriate enhancement of the auxiliary basis itself.

To demonstrate the general applicability of our approach, we first discuss HF and MP2 total energies for RI-V and RI-LVL in FHI-aims using Gaussian basis sets and compare them to the results obtained with NWChem. We then show that the same degree of accuracy can be obtained using the NAO basis functions of FHI-aims.

3.1.1. Gaussian type orbitals

To establish a valid reference for our comparison between RI-V and RI-LVL, we first calculate total energies for the molecular geometries compiled in the S22 test set of Jurečka and coworkers [58] with the Gaussian basis set cc-pVTZ [59]. This test set contains 22 weakly bonded dimers with 6–30 atoms per dimer, ranging from the water dimer to adenine–thymine complexes. This test set allows us to test total energies of molecular systems as well as weak binding energies, which usually require RPA or MP2 for an accurate description. Figure 3 shows the total energy errors for all molecular dimers and table 1 shows the root mean square deviation (RMSD) and maximum absolute value (MAX) for the error per atom (not counting hydrogens) and the systemwide error. The results show that the RI-V implementation in FHI-aims is reliable and accurate [32], yielding deviations in total energy of less than 1 meV per system for HF calculations. Also the MP2 corrections, which are more sensitive to the accuracy of the four-center integrals, are of similar quality, with a RMSD below 0.2 meV. Our RI-V implementation is therefore a suitable reference choice to benchmark RI-LVL and will be employed as such throughout the rest of this work.

Zoom In Zoom Out Reset image size

Table 1.  Root mean square deviation and maximum (absolute) value of the total energy error (total and per atom, not counting hydrogens) of RI-V in the S22 test set compared to NWChem using the cc-pVTZ basis set. (See also figure 3.)

${\rm{\Delta }}{E}_{\mathrm{tot}}$		HF		MP2
(meV)		RMSD	MAX	RMSD	MAX
RI-V	Total	0.383	0.716	0.182	0.445
	per atom	0.038	0.082	0.028	0.085
RI-LVL	Total	9.129	18.423	168.995	440.565
	per atom	0.743	1.062	11.432	29.371
RI-LVL +aux	Total	0.527	0.936	0.581	1.144
	per atom	0.051	0.087	0.055	0.111

Table 2.  RMSD and maximum absolute errors for Hartree–Fock calculations in the S22 test set using the RI-V method with tier 2 basis sets. The functions listed under 'aux basis additions' are added to those from the bare basis set when the product basis is constructed.

$\mathrm{HF}\;\mathrm{RI}-{\rm{V}}$	${\rm{\Delta }}{E}_{\mathrm{tot}}$ (meV)
Aux basis	Per atom		Systemwide
additions	RMSD	MAX	RMSD	MAX
s(z = 1)	0.005	0.016	0.040	0.124
sp(z = 1)	0.009	0.024	0.090	0.201
spd(z = 1)	0.011	0.020	0.119	0.318
spdf(z = 1)	0.023	0.064	0.341	1.219
spdfg(z = 1)	0.154	0.367	2.320	6.976

The straightforward localized RI on the other hands yields significantly higher errors of up to 29.5 meV/atom (up to 440 meV total error) for MP2 calculations and also gives less accurate results for HF, although the discrepancies there are less dramatic. However, the plot also shows an additional set of curves, labeled 'RI-LVL+aux', which corresponds to RI-LVL with an enhanced auxiliary basis (using a single hydrogenic g function with z = 6). This data set shows that RI-LVL yields an accuracy similar to RI-V provided a suitable chosen OBS+ and thus auxiliary basis set $\{{P}_{\mu }({\bf{r}})\}$ is chosen. We will discuss the choice of OBS+ in detail below. (The interested reader is referred to appendix B for more details about the impact of the g-function.)

In addition to the S22 test set we also investigated the performance of our new method in the larger G3 test set [60]. This test set contains 223 molecules composed of first and second row elements. As in the S22 case we used NWChem as a reference for our RI implementations. The results for HF and MP2 total energies are shown in figure 4. We have not included the 28 dimer systems in the statistical analysis, because RI-V and RI-LVL are the same procedures for dimer systems.

Zoom In Zoom Out Reset image size

Overall, RI-V achieves a very good accuracy with an RMSD of the total energy of about 1 meV. As was already the case in the S22 test set, RI-LVL itself performs worse and yields errors with tens or even hundreds of meV magnitude. However, enhancing the auxiliary basis with the same functions we used in the S22 test set, we can again recover the same accuracy as RI-V. A few test cases still exhibit total energy errors up to 5.5 meV. For all these cases the RI-LVL results lie exactly on top of the RI-V results, which is a strong indication that these errors are not specific to RI-LVL. It should also be noted that almost all the outliers contain chlorine atoms.

3.1.2. Numeric atom-centered orbitals

For the remainder of the article, we will return to the NAO basis sets and focus on improving the accuracy of RI-LVL. For HF calculations we use the standard tier 2 basis sets [16] with tight settings. For MP2 calculations, on the other hand, we use the recently developed valence correlation consistent NAO basis sets [61].

As seen in figure 3, our standard procedure to construct the $\{{P}_{\mu }({\bf{r}})\}$ yields sufficiently accurate total energies at the HF level. However, it does not suffice to converge MP2 total energies with our localized RI. A straightforward way to deal with this error is to increase the size of the auxiliary basis. This is achieved by using OBS+ instead of OBS for the construction of the auxiliary basis set, as discussed in section 2.3.

We first show that our reference is well converged with respect to the auxiliary basis by enhancing the original OBS with functions of increasing angular momentum (see upper panel in figure 5). Then we apply the same systematic approach to RI-LVL and finally we demonstrate that an OBS+ with only a single extra g function (see lower panel in figure 5) is sufficient.

Zoom In Zoom Out Reset image size

Table 2 njp518333t1 shows the impact of this enhanced $\{{P}_{\mu }({\bf{r}})\}$ on the HF total energies calculated with RI-V. Even if the auxiliary basis set is significantly enlarged with extended functions having high angular momenta, the change in total energy is below 0.16 meV per atom (max 0.37 meV).

Figure 6 shows that the error of RI-LVL systematically converges with increasing auxiliary basis set size. By including additional radial functions with angular momentum s, p, d, f and g in the auxiliary basis construction the RMSD of the total energy per atom can be reduced from 1.9 to 0.13 meV. Therefore, the error introduced in a HF calculation by using the local RI approximation can be controlled systematically by adding higher angular momenta to the $\{{P}_{\mu }({\bf{r}})\}$ and decreases to a negligible value.

In figure 6 it can be seen that the addition of f and g functions has the largest impact. It turns out that a single g function is already sufficient. As shown in table 3, the accuracy of the hierarchical approach can even be surpassed if we alter the effective charge that defines the added g function, but the general quality of the result is unaffected by the choice of the effective charge. The reason why the results do not depend strongly on the shape (see lower panel of figure 5) of the added function is the basis-confining potential (see equation (9)). As can be seen in figure 5, the onset and peak position of the radial function depends on the effective charge, but their behavior in the outer regions is similar. Without the confinement potential, the radial functions would extend further and the results would probably show a significant dependence on the effective charge.

Zoom In Zoom Out Reset image size

Table 3.  RMSD and maximum absolute errors for Hartree–Fock calculations in the S22 test set using the RI-LVL method with tier 2 basis sets. The functions listed under 'aux basis additions' are added to those from the bare basis set when the product basis is constructed.

HF RI–LVL	${\rm{\Delta }}{E}_{\mathrm{tot}}$ (meV)
Aux basis	Per atom		Systemwide
additions	RMSD	MAX	RMSD	MAX
None	0.594	1.891	3.959	6.432
spdfg(z = 1)	0.052	0.124	0.493	1.466
g(z = 1)	0.066	0.153	0.633	1.799
g(z = 2)	0.059	0.137	0.567	1.663
g(z = 3)	0.054	0.127	0.533	1.590
g(z = 4)	0.053	0.125	0.514	1.544
g(z = 5)	0.053	0.123	0.491	1.454
g(z = 6)	0.047	0.107	0.465	1.305
g(z = 7)	0.046	0.098	0.462	1.226

We also investigated the use of RI-LVL in MP2 calculations. For these calculations we use the recently developed compact NAO based valence correlation consistent basis sets [61] that facilitate an extrapolation to the complete basis set limit.

As can be seen from table 4, RI-V with the 3Z-version of these basis sets is essentially insensitive to an enlarged auxiliary basis set, yielding at most a change of 0.1 meV per atom compared to the pure basis set. In the following analysis, RI-V with the NAO-VCC-3Z basis set with the standard auxiliary basis set will therefore be used as the reference to benchmark the MP2 results.

Table 4.  RMSD and maximum absolute errors for MP2@HF in the S22 test set using the RI-V method with the NAO-VCC-3Z basis set. The functions listed under 'aux basis additions' are added to those of the bare basis set when the product basis is constructed.

MP2@HF RI–V	${\rm{\Delta }}{E}_{\mathrm{tot}}$ (meV)
Aux basis	Per atom		Systemwide
additions	RMSD	MAX	RMSD	MAX
s(z = 1)	0.003	0.008	0.031	0.076
sp(z = 1)	0.013	0.045	0.050	0.123
spd(z = 1)	0.012	0.036	0.066	0.126
spdf(z = 1)	0.011	0.027	0.076	0.144
spdfg(z = 1)	0.031	0.098	0.494	1.856

Figure 7 shows the accuracy for MP2 using the same representation as figure 6 did for HF. In essence, we find the same results as for HF: if functions up to angular momentum channel f are included in OBS+, the error can be reduced to 0.43 meV per atom (6.52 meV for the system) at most, while an additional g function reduces the error even further to at most 0.11 meV per atom (1.15 meV for the system). As for HF and the tier basis, the accuracy of the hierarchical approach can also be achieved with fewer auxiliary basis functions. Table 5 shows that a single g-function reduces the total energy error to the same order of magnitude as the addition of s, p, d, f and g functions. As for HF we find that the general quality of the results is insensitive to the variation of the effective charge, but can be fine-tuned to yield errors slightly below those of the systematic approach.

Zoom In Zoom Out Reset image size

Table 5.  RMSD and maximum absolute errors for MP2@HF in the S22 test set using the RI-LVL method with the NAO-VCC-3Z basis set. The functions listed under 'aux basis additions' are added to those of the bare basis set when the product basis is constructed.

MP2@HF RI–LVL	${\rm{\Delta }}{E}_{\mathrm{tot}}$ (meV)
Aux basis	Per atom		Systemwide
additions	RMSD	MAX	RMSD	MAX
None	13.919	32.970	195.751	494.545
spdfg(z = 1)	0.047	0.104	0.548	1.141
g(z = 1)	0.063	0.111	0.859	2.006
g(z = 2)	0.064	0.114	0.881	2.003
g(z = 3)	0.059	0.104	0.814	1.879
g(z = 4)	0.054	0.097	0.737	1.780
g(z = 5)	0.036	0.070	0.483	1.324
g(z = 6)	0.028	0.074	0.364	1.035
g(z = 7)	0.046	0.082	0.610	1.384

To demonstrate RI-LVL's broad range of applicability, we also performed calculations with the PBE0 exchange-correlation functional [8] and the RPA [12–14].

For PBE0 we use tier 2 basis sets, as we did for HF. For converged RPA total energies, larger NAO basis sets are required [62] and we thus use the NAO-VCC-3Z basis set again. As in the cases of HF or MP2, for PBE0 the RI-V shows no significant dependence on the added auxiliary basis functions (data not shown). When the product basis is enhanced with additional auxiliary functions, the RI-LVL results can be controlled and converged in a systematic way. In contrast to the previous HF calculations (see figures 3 and 6), we find that no OBS+ is needed to obtain accurate results with PBE0. This has two reasons: first, compared to the cc-pVTZ basis set used in figure 3 the tier 2 basis already contains a g-function in the orbital basis set. (See table 10 for more details on the tier basis sets and table 12 for an example of how the auxiliary basis set is enhanced by the additional g function.) The second reason is that PBE0 only contains 25% exact exchange, which reduces the total energy error accordingly, when compared to the tier 2 HF calculations.

Table 6 shows the relevant errors for the hierarchical enhancement of the auxiliary basis. As for HF, we can significantly reduce the RMSD and maximal value of the total energy error per atom, in this case by more than one order of magnitude from 0.19 to 0.02 meV. If the auxiliary basis is only enhanced by a single g-function, we find results similar to those from the HF analysis: the effective charge of extra function in the OBS+ has no significant impact on the achieved accuracy.

Table 6.  RMSD and maximum absolute errors for PBE0 in the S22 test set using the RI-LVL method with the tier 2 basis set. The functions listed under 'aux basis additions' are added to those of the bare basis set when the product basis is constructed.

PBE0 RI–LVL	${\rm{\Delta }}{E}_{\mathrm{tot}}$ (meV)
Aux basis	Per atom		Systemwide
additions	RMSD	MAX	RMSD	MAX
None	0.068	0.185	0.543	0.941
s(z = 1)	0.070	0.188	0.557	0.964
sp(z = 1)	0.060	0.159	0.464	0.792
spd(z = 1)	0.039	0.091	0.334	0.588
spdf(z = 1)	0.012	0.028	0.115	0.237
spdfg(z = 1)	0.007	0.017	0.065	0.168

For RPA@PBE0 calculations using the NAO-VCC-3Z basis set we find almost the same behavior as for MP2: the RI-V reference is again well converged and shows no sensitivity to the added auxiliary basis functions (data not shown) and the RI-LVL error can be well controlled by the hierarchical auxiliary basis set additions, as shown in figure 8 for the RMSD and maximal absolute error. The only difference we found is that the reduction of the additional auxiliary basis functions to a single g-function is not as effective as for the HF/MP2 case. In table 7 we listed the RMSD and maximal absolute errors for different effective charges of the added g-function. As can be seen, the values are significantly larger than for the largest analyzed hierarchical auxiliary basis set, but still small on an absolute scale. The error per atom is below 0.5 meV in all cases and the RMSD for the total error is approximately 0.8 meV.

Zoom In Zoom Out Reset image size

Table 7.  Root mean square deviation and maximum absolute errors for RPA@PBE0 in the S22 test set using the RI-LVL method with the NAO-VCC-3Z basis set. The functions listed under 'aux basis additions' are added to those of the bare basis set when the product basis is constructed.

RPA@PBE0 RI–LVL	${\rm{\Delta }}{E}_{\mathrm{tot}}$ (meV)
Aux basis	Per atom		Systemwide
additions	RMSD	MAX	RMSD	MAX
None	9.119	17.611	120.283	266.504
spdfg(z = 1)	0.041	0.130	0.221	0.597
g(z = 1)	0.059	0.385	0.792	7.324
g(z = 2)	0.060	0.383	0.795	7.286
g(z = 3)	0.059	0.387	0.791	7.353
g(z = 4)	0.058	0.390	0.785	7.416
g(z = 5)	0.059	0.406	0.796	7.712
g(z = 6)	0.058	0.417	0.804	7.932
g(z = 7)	0.057	0.402	0.788	7.642

In addition to total energies we also computed the atomization energies in the G2–1 test set [66, 67] and reaction barrier heights in the BH76 test set [6, 68] with RI-LVL. The employed geometries are taken from the original papers. For the G2–1 test set we included only those molecules in the error analysis which have at least three atoms, because RI-V and RI-LVL are identical in the dimer case. In the RI-LVL calculations we use an auxiliary basis set constructed from an OBS+ with a g function with z = 6. All RI-V calculations are performed with the standard OBS and $\{{P}_{\mu }({\bf{r}})\}$. All calculations use the NAO-VCC-3Z OBS. As shown in table 8, RI-LVL performs equally well for binding energies as for total energies.

In addition to the properties of light elements from the first and second row of the periodic table, we also investigated the performance of RI-LVL for a few representative heavier elements, namely copper, gold and titanium dioxide. The cluster geometries used for this test are displayed in figure 9.

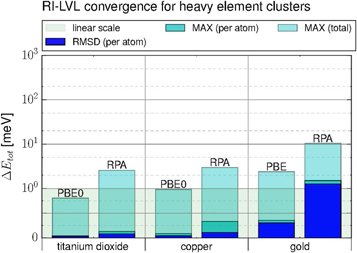
Zoom In Zoom Out Reset image size

Figure 10 shows the RMSD and maximum absolute error per atom for titanium dioxide, copper and gold clusters. For the heavy elements we used either tier 3 (titanium, oxygen and gold) or tier 4 (copper) basis sets to demonstrate the applicability of our new method to a typical RPA-calculation setup. We know from the previous results that light elements like oxygen need an enhanced auxiliary basis set for an accurate treatment with RI-LVL. Therefore, we constructed an enhanced auxiliary basis set with an additional g-function (z = 1) for oxygen in titanium dioxide. For the explicit three-center integrals $({ij}| \mu )$ of RI-V, dense multicenter integration grids are needed for heavy elements. We note that the $({ij}| \mu )$ integrals are two-center in RI-LVL and can be carried out using Talman's method, therefore significantly lighter integration grids are sufficient for our RI-LVL implementation than for RI-V. With very tight integration settings (see appendix C for the details) particularly for RI-V, our RI-LVL results match the total energies of RI-V for our chosen systems with an RMSD below 1.3 meV per atom even for gold clusters. In contrast to lighter elements, our results suggest that the auxiliary basis is well saturated and has enough flexibility to compute the four-center integrals accurately without adding further elements to the OBS.

Zoom In Zoom Out Reset image size

To substantiate this observation, we computed the systems again with a g-function in the OBS+ and otherwise identical parameters. The results are shown in table 9.

Table 9.  For RI-V and RI-LVL, we show the RPA@PBE0 total energy change (RMSD) of the clusters shown in figure 9 when adding a g-function (z = 6) to the OBS of the elements Ti, Cu, and Au. For all titanium dioxide test cases, we used an OBS+ with an additional g-function on oxygen, i.e., the third column only reflects the RMSD change due to the addition of a g-function to the OBS of Ti. See text for further details about the computational settings.

RPA-RMSD per atom		RMSD per
OBS+ with g[z = 6] versus standard OBS		atom (meV)
Gold	RI-V	0.438
OBS: tier 3	RI-LVL	0.187
Copper	RI-V	0.193
OBS: tier 4	RI-LVL	0.043
Titanium dioxide	RI-V	0.101
OBS: tier ${3}^{*}$	RI-LVL	0.022

Enhancing the RI-LVL calculations with additional auxiliary basis functions on the heavy elements changes the results only slightly. The RI-V calculations on the other hand show a larger, but overall still insignificant susceptibility to the additional functions in the $\{{P}_{\mu }({\bf{r}})\}$. For example the RMSD changes by 0.44 meV for gold when computed with RI-V, while RI-LVL only exhibits a change of 0.19 meV.

From the presented RMSD and maximum errors (figure 10) we can see that RI-LVL is very accurate for heavy elements and can reproduce the RI-V results with no significant error. The deviation for the error per atom is consistently below 1.5 meV and even the total error is a few meV at most for large basis sets. We have additionally verified that these conclusions also hold for smaller FHI-aims tier1 basis sets as the OBS for Ti, Cu, and Au, with maximum overall errors between RI-LVL and RI-V for RPA of 3 meV (Au₇) and errors for the PBE0 hybrid functional consistently below 1 meV. The good performance for all three elements shows that the RI-LVL has no problems dealing with d- and f-electrons.