Multiplons in the two-hole excitation spectra of the one-dimensional Hubbard model

Let us start the discussion of the results with the simple case of the completely filled band: n = 2. Creating two holes with opposite spins constitutes a two-body problem and a closed analytical expression for the excitation spectrum is readily derived [20, 21, 24]. Alternatively, one may apply the Chebyshev expansion method using exact states for rather large systems, since the Hilbert-space dimension is merely L². Some numerical results for L = 1000 and periodic boundary conditions are shown in figure 1.

Zoom In Zoom Out Reset image size

The two-hole spectra for different U can be understood as follows: if U = 0, one can straightforwardly evaluate equation (5) by Fourier transformation to reciprocal space. This yields

$$\begin{eqnarray}&&{A}_{2-\mathrm{hole}}^{(0)}(\omega )=\int {\rm{d}}x\;{\rho }_{0}(x){\rho }_{0}(\omega -x),\end{eqnarray} \tag{ 16 }$$

where ${\rho }_{0}(x)={L}^{-1}\sum _{k}\delta (x-\varepsilon (k))$ and $\varepsilon (k)=-2t\mathrm{cos}(k)$, i.e., the two-hole spectrum is given by the self-convolution of the non-interacting density of states [46]. The self-convolution of the one-dimensional density of states ${\rho }_{0}(x)$ is just given by the two-dimensional one with bandwidth $2W=8t$ (see black line). The two conduction-band holes move independently of each other through the lattice.

Upon increasing U, a sharp satellite emerges at the lower edge of this 'band-like part' of width $2W$ and moves to higher binding energies [20, 21]. For $U\gg t$ it is approximately separated by U from the barycenter of the band-like part located at $\omega =-4t$. This corresponds to the formation of a stable two-hole bound state which we will call 'doublon' in the rest of the paper. Since the one-hole spectrum has a finite support, a decay of the doublon into independent holes is prohibited by energy conservation for large U. One-dimension is in fact special in that there is a bound two-hole state outside the continuum for any $U\gt 0$, so that momentum conservation must be considered as well to understand its stability [8]. This is very similar to the Bose case discussed in [5].

The finite width of the satellite reflects the fact that the doublon is itinerant. For strong U the propagation of a single doublon is perturbatively described by a second-order hopping process and is captured by the effective Hamiltonian (see also equation (27) below)

$$\begin{eqnarray}&&{H}_{{\rm{eff}}}=\displaystyle \frac{2{t}^{2}}{U}\displaystyle \sum _{\langle {ij}\rangle }({d}_{i}^{\dagger }{d}_{j}+{\rm{h.c.}})+\left(\displaystyle \frac{4{t}^{2}}{U}+U\right)\displaystyle \sum _{i}{n}_{i}^{d},\end{eqnarray} \tag{ 17 }$$

where ${d}_{i}^{\dagger }={c}_{i\uparrow }^{\dagger }{c}_{i\downarrow }^{\dagger }$ is a bosonic doublon creator and ${n}_{i}^{d}={d}_{i}^{\dagger }{d}_{i}$. Hence, in the strong-coupling limit the satellite has the shape of the non-interacting density of states with a rescaled bandwidth of $8{t}^{2}/U$. With increasing U, the doublon satellite gains more and more spectral weight at the expense of the band-like part and eventually results in a δ-peak for $U=\infty$, corresponding to a completely immobile doublon.

In the strong-U limit, the physics can be visualized to some extent by typical electronic configurations contributing to the different spectral features. Figure 2 gives a sketch of the different configurations contributing to the doublon satellite 'D' and to the band-like part 'B'.

Zoom In Zoom Out Reset image size

We now turn to the case of a conduction band with a finite hole density: $n\lt 2$. This changes the situation completely as the two additional holes placed with opposite spins at site i interact with a thermodynamically relevant fraction of holes in the incompletely filled band. From the technical point of view, the computation of the spectrum transmutes into a severe many-body problem: a comprehensive and reliable study, however, is possible when tolerating a non-zero low-energy cutoff in the form of a finite spectral resolution $\delta E$. Using the Chebyshev technique combined with MPSs, we have been able to study the excitation spectra in the entire filling range $1\leqslant n\leqslant 2$ for the Hubbard model on lattices as large as L = 60 at a constant energy resolution $\delta E\approx 0.2t$. With $\delta E\lesssim 0.2t$ one would start to resolve finite-size artifacts. Calculations have been performed for systems with open boundary conditions and choosing i as a central site in the chain (see equations (5) and (6)).

Figure 3 provides an overview and shows the filling dependence of the spectrum at $U=6t$, chosen such that for n = 2, the doublon satellite is clearly separated from the band-like part. Several distinct effects arise at finite hole density, which we discuss now in turn:

Zoom In Zoom Out Reset image size

First of all, the overall intensity of the two-hole spectrum in the range $\omega \lt 0$ is seen to decrease with decreasing filling. This is a consequence of the sum rule for the double occupancy

$$\begin{eqnarray}&&\langle {n}_{i\uparrow }{n}_{i\downarrow }\rangle ={\displaystyle \int }_{-\infty }^{0}{\rm{d}}\omega \;{A}_{2-\mathrm{hole}}(\omega ),\end{eqnarray} \tag{ 18 }$$

which is straightforwardly derived from equation (5), and of the fact that $\langle {n}_{i\uparrow }{n}_{i\downarrow }\rangle$ is decreasing with n.

The doublon satellite ('D') is still present with strong weight at $U=6t$ but its support broadens significantly with decreasing n. The satellite can be traced down to fillings close to half-filling. Right at n = 1 it vanishes completely. An extended discussion is given in section 3.3.

A continuation of the 'band-like part' ('B') of the two-hole spectrum is also clearly visible, at least down to $n\approx 1.5$. When the filling approaches half-filling, however, the weight of the band-like part becomes very small, and the structure is hardly visible at low energies, say $-2\lesssim \omega \lt 0$, for fillings $1\lt n\lt 1.2$. Note, however, that there is finite spectral weight for $\omega \to 0$ at any filling $n\gt 1;$ only at half-filling, n = 1, is the spectrum gapped.

As soon as $n\lt 2$, the spectrum exhibits an additional structure, marked as 'T' in figure 3. For fillings $n\to 2$ it shows up as a tiny peak at high binding energies. It gains some spectral weight upon decreasing n and moves towards $\omega =0$, until it completely merges with the doublon satellite. At the same time, another peak can be seen emerging within the spectral range of the doublon satellite (seen best for n = 1.6 at $\omega \approx -8.7t$). It moves towards $\omega =0$ at the same rate and also belongs to 'T'. The structure 'T' will be interpreted as a 'triplon' in section 3.5.

The physics close to and at half-filling is complicated by the appearance of yet another structure 'Q' which emerges for $n\lesssim 1.5$ at the highest binding energies and gains more and more weight as n approaches half-filling. This feature will be addressed in section 3.6 and interpreted as a 'quadruplon'.

At half-filling the system is a Mott insulator. The gap in the one-particle spectral function is accessible to the Bethe-ansatz method [47] and can be computed from the exact expression [48]

$$\begin{eqnarray}&&{\rm{\Delta }}=\displaystyle \frac{16{t}^{2}}{U}{\displaystyle \int }_{1}^{\infty }{\rm{d}}x\ \displaystyle \frac{\sqrt{{x}^{2}-1}}{\mathrm{sinh}(2\pi x\;t/U)}.\end{eqnarray} \tag{ 19 }$$

At $U=6t$ it amounts to ${\rm{\Delta }}={\mu }_{+}-{\mu }_{-}\approx 2.89t$. As figure 3 demonstrates, the two-particle spectral function is gapped as well, but by twice the one-particle gap $2{\rm{\Delta }}\approx 5.86t$ (the numerical value is obtained from the ground-state energies, and the slight discrepancy compared to twice of the Bethe-ansatz value is due to the finite system size).

Note that the chemical potential jumps from $\mu ={\mu }_{-}$ for $n\;\nearrow \;1$ to $\mu ={\mu }_{+}$ for $n\;\searrow \;1$ and is not uniquely defined at half-filling² . The two-hole and the two-particle spectrum for n = 1 in figure 3 have been calculated for the choice $\mu =({\mu }_{+}+{\mu }_{-})/2\quad =\quad U/2\quad =\quad 3t$, which implies a symmetric spectrum ${A}_{2}(-\omega )={A}_{2}(\omega )$. If $\mu ={\mu }_{+}$ had been chosen, the n = 1 spectrum would have evolved continuously from the spectrum for $n\gt 1$. Hence, the single broad peak in the two-hole spectrum at n = 1, which takes the whole spectral weight, smoothly connects to the quadruplon peak 'Q' at higher fillings.

For fillings below half-filling, $n\lt 1$, the two-hole spectrum is related to the two-particle spectrum for $n\gt 1$ via the relation equation (8). As is seen for $\omega \gt 0$ in figure 3, it consists of a single peak, smoothly connected to 'Q' which just continues to lose spectral weight until it vanishes for $n\to 0$. The vanishing of the weight is related to sum rule for the two-particle spectrum

$$\begin{eqnarray}&&\langle (1-{n}_{i\uparrow })(1-{n}_{i\downarrow })\rangle ={\displaystyle \int }_{0}^{\infty }{\rm{d}}\omega \;{A}_{2-\mathrm{particle}}(\omega ),\end{eqnarray} \tag{ 20 }$$

which is straightforwardly derived from equation (6), and to the fact that the average number of empty sites goes to zero for $n\to 2$, i.e., the phase space for creating two additional particles at a site i vanishes.

Let us also mention that the difference between the total weights of the two-hole and the two-particle spectrum is given by the filling:

$$\begin{eqnarray}&&{\displaystyle \int }_{-\infty }^{0}{\rm{d}}\omega \;{A}_{2-\mathrm{hole}}(\omega )-{\displaystyle \int }_{0}^{\infty }{\rm{d}}\omega \;{A}_{2-\mathrm{particle}}(\omega )=n-1.\end{eqnarray} \tag{ 21 }$$

This is a direct consequence of equations (18) and (20).

For fillings close to the simple n = 2 limit, the physical interpretation of the doublon peak 'D' as a repulsively bound pair of holes is still self-evident. With decreasing n, and for fillings close to half-filling in particular, the validity of this picture must be questioned seriously.

First of all, as soon as $n\lt 2$, the doublon starts to interact with a continuum of electron–hole excitations, such that the corresponding peak should actually be seen as a resonance with a finite lifetime rather than an exact eigenstate of the Hamiltonian (for a given wave vector). This will be discussed in detail in section 3.8.

In fact, the doublon peak broadens with decreasing n. Its support widens from a value slightly larger than ${\rm{\Delta }}\omega =8{t}^{2}/U=4t/3$, which is the perturbative result for $U\to \infty$ at n = 2, to ${\rm{\Delta }}\omega \gtrsim 4t$ for fillings close to, but above half-filling.

To understand the main reason for this broadening, consider the spectrum for a system with $N=L+1$ particles, i.e., for a filling slightly above half-filling n = 1. Figure 4 provides a sketch. The support of the doublon peak is given by the spectral range of the final states. As indicated in the sketch, the dominating final-state configurations are characterized by a hole moving through a lattice of half-filled sites. This is a standard many-body problem, intensively discussed, e.g., in the context of the Mott–Hubbard metal-insulator transition [49]: double occupancies are effectively suppressed at strong U, well-formed local magnetic moments emerge and develop strong antiferromagnetic correlations due to the Anderson super-exchange mechanism. While the effective coupling constant $J=4{t}^{2}/U$ of the latter is derived in second-order-in-t perturbation theory and is small, the motion of the hole takes places on the large energy scale t. Neglecting J altogether, already provides the right width of about $4t$ for the doublon peak, consistent with the corresponding spectrum displayed in figure 3.

Zoom In Zoom Out Reset image size

Let us mention that the arguments can be formalized by considering the standard mapping of the low-energy sector of the Hubbard model for strong U onto the t–J model [50]. Close to half-filling it reads:

$$\begin{eqnarray}&&{H}_{t-J}=-t\displaystyle \sum _{\langle {ij}\rangle ,\sigma }({\tilde{c}}_{i\sigma }^{\dagger }{\tilde{c}}_{j\sigma }+{\rm{h.c.}})+J\displaystyle \sum _{\langle {ij}\rangle }{{\boldsymbol{S}}}_{i}{{\boldsymbol{S}}}_{j},\end{eqnarray} \tag{ 22 }$$

where ${{\boldsymbol{S}}}_{i}=\frac{1}{2}{\sum }_{\sigma {\sigma }^{\prime }}{c}_{i\sigma }^{\dagger }{{\boldsymbol{\sigma }}}_{\sigma {\sigma }^{\prime }}{c}_{i{\sigma }^{\prime }}$ is the spin at site i, ${\boldsymbol{\sigma }}$ the vector of Pauli matrices and where ${\tilde{c}}_{i\sigma }$ is the annihilator in the subspace with no double occupancies. Neglecting J yields the t model which exactly maps [51] onto the ${J}_{{\rm{KL}}}=\infty$ Kondo lattice. For a single hole in the t model or, equivalently, a single electron in the Kondo lattice, the ground state is a ferromagnet as is known from Nagaoka's work [52] or, equivalently, can be proven [53] for the Kondo lattice. The width $4t$ is obvious then. For the present case with finite U, a somewhat larger width is expected.

Another helpful observation is that the final states of the two-hole spectroscopy (see figure 2(b)) are the same as the final states of the one-hole spectroscopy, i.e., photoemission, but from an exactly half-filled conduction band with N = L electrons. The (raw) photoemission spectrum is given by the one-hole spectral function

$$\begin{eqnarray}{A}_{1-\mathrm{hole},\sigma }(\omega ) & = & \displaystyle \sum _{n}{| \langle n,N-1| {c}_{i\sigma }| 0,N\rangle | }^{2}\\ & & \times \delta (\omega +\mu -({E}_{0}^{(N)}-{E}_{n}^{(N-1)})).\end{eqnarray} \tag{ 23 }$$

This shows that the support of the doublon peak must be the same as the support of the photoemission spectrum. The latter has indeed a width of ${\rm{\Delta }}\omega \gtrsim 4t$ at $U=6t$, as can be read off from the DMRG results shown in figure A1 of appendix A. As the matrix elements for the two-hole spectroscopy are different, however, the shape of the doublon satellite is different and, at least on this level, it is difficult to make contact with the well-known spinon and holon excitations that govern the one-hole spectrum.

We conclude that the concept of a doublon as a repulsively bound pair of holes breaks down for fillings close to half-filling. The main difference is that the doublon moves in a background of singly occupied sites and explores antiferromagnetic correlations. This strongly affects its mobility. For $n\to 1$ the doublon propagates on the energy scale of about $4t$, opposed to the energy scale $8{t}^{2}/U$ set by double-hopping processes in the high-density limit. The strong decrease of the weight of the doublon peak with decreasing n is related to the decreasing density of doubly occupied sites in the respective initial ground state. The shift of the position of the doublon satellite is closely related to the filling dependence of the band-like part.

The band-like part 'B' of the two-hole spectrum results from the continuum of unbound two-hole final states. For n = 2 and U = 0, this is given by the self-convolution of the density of states ${\rho }_{0}(x)$. With increasing U it quickly loses weight in favor of the doublon satellite (see figure 2) and becomes an almost featureless structure for strong U whose shape still loosely resembles the self-convolution of the density of states, but without the strong van Hove singularities. Its weight is already low for $U=6t\gt W$, see figure 1.

For fillings close to half-filling, this scenario still holds to a good approximation, but with the density of states replaced by its occupied part only (for a given filling). Since the occupied fraction shrinks with decreasing n, the weight of the band-like part must diminish and its spectral support narrow down, with the barycenter shifting upwards. This effect is clearly visible in figure 3 for high fillings.

The barycenter of the band-like part also fixes the position of the doublon satellite which is found at an energy of about U below. Assuming a rectangular density of states with bandwidth $W=4t$, we have ${\omega }_{0}=-(n/2)W$ for the barycenter and ${\rm{\Delta }}\omega ={nW}$ for the width of the band-like part. This simple model roughly explains the trend seen for fillings $n\gtrsim 1.6$. For example, the model predicts ${\omega }_{0}=-3.2t$ for n = 1.6 resulting in $\omega =-(n/2)W-U=-9.2$ for the satellite position. This should be compared with the barycenter of the satellite at $\omega \approx -8.75t$ in figure 3 (obtained by integrating the data).

For fillings $n\lesssim 1.5$, however, ${\omega }_{0}$ shifts much faster with decreasing n and the model breaks down (note that there is a finite band-like part for any $n\gt 1$). In this filling range, one may consider the two additional holes in the final state as moving independently of each other, but strongly interacting with the high hole density in the ground state.

This can be very roughly described in the following way: we replace the non-interaction density of states ${\rho }_{0}$ by an interacting density of states ρ which is assumed to consist of two Hubbard peaks, separated in energy by U. For $n\geqslant 1$ and following the standard theory [54] of filling-dependent spectral-weight transfer in the strong-coupling limit, the lower Hubbard band has the weight $2-n$ and is fully occupied, while the upper Hubbard band is partially occupied with the occupied fraction having the weight $2n-2$ (and the unoccupied fraction having weight $2-n$). In the simple model the band-like part is then proportional to the self-convolution of the low-energy part of the occupied density of states ρ, i.e., of the occupied part of the upper Hubbard band (UHB). Assuming that the shape of the latter is n-independent, we find ${\omega }_{0}=-(n-1)W$.

This roughly explains the filling dependence of the doublon satellite for $n\lesssim 1.6t$. For example, we have ${\omega }_{0}=-0.8t$ for n = 1.2, resulting in $\omega =-(n-1)W-U=-6.8t$ for the satellite position. This compares well with the DMRG results in figure 3 where we find $\omega \approx -6.3t$. For $n\to 1$, in particular, the model predicts a vanishing band-like part with ${\omega }_{0}\to 0$, and the resulting position of the doublon satellite at $\omega \approx -U$ agrees well with the data.

Although the model is surely oversimplified, it illustrates that the filling-dependent spectral-weight transfer is important for the location of the continuum of unbound two-hole final states, and thus for the doublon satellite as well.

The most apparent deviations from the standard Cini–Sawatzky theory consist in the appearance of the new structures 'T' and 'Q'. Let us first concentrate on 'T' which already shows up for low hole-densities $n\lesssim 2$, a limit which has been studied to some extent using the ladder approximation in the hole–hole channel [25, 26].

When acting with ${c}_{i\uparrow }{c}_{i\downarrow }$ on the ground state, one may distinguish between contributions to the spectrum resulting from two different types of ground-state configurations: in the case of an excitation that takes place in a hole-free region, one expects essentially the same shape of the spectrum as in the n = 2 case. For $n\to 2$ this is the dominant contribution. If the excitation takes place at a site i next to an already existing hole, however, a final state with three holes on nearest-neighboring sites is created. This case is schematically illustrated with figure 5.

Zoom In Zoom Out Reset image size

Here, the question arises whether the three holes can form a new bound object, a 'triplon'. Since this question addresses the excited states one projects onto in equation (5), rather than the ground state, we first study the three-hole excitation spectrum

$$\begin{eqnarray}{A}_{3-\mathrm{hole},\sigma }(\omega ) & = & \displaystyle \sum _{n}{| \langle n,N-3| {c}_{i\uparrow }{c}_{i\downarrow }{c}_{i+1\sigma }| 0,N\rangle | }^{2}\\ & & \times \delta (\omega +3\mu -({E}_{0}^{(N)}-{E}_{n}^{(N-3)}))\end{eqnarray} \tag{ 24 }$$

for the completely filled band (n = 2). This involves the same type of final states while the ground state is trivial, and we are left with a much simpler three-body problem only. Since the Hilbert-space dimension is approximately ${L}^{3}/2$, we can use the Chebyshev expansion method with exact states.

The result for L = 500 sites is shown in figure 6. One observes a similar general pattern as in the two-hole case: For U = 0 the spectrum consists of a three-fold self-convolution of ${\rho }_{0}(\omega )$ with a spectral width given by $3W=12t$, while for finite $U\gt 0$, there is a band-like part and a split-off correlation satellite.

Zoom In Zoom Out Reset image size

For finite but strong U, the satellite in ${A}_{3-\mathrm{hole},\sigma }(\omega )$ has a slightly asymmetric weight distribution due to the presence of the band-like part. Apart from that, its shape is given by a convolution of ${\rho }_{0}(\omega )$ (the single hole, width W) with the same density of states, but rescaled (the doublon, width ${\rm{\Delta }}\omega =8{t}^{2}/U$), see the inset in figure 6. This clearly indicates that the doublon and the hole propagate independently and do not form a bound state.

This should also hold for the two-hole spectrum (figure 3): the structure 'T' does not represent a stable triplon, but is rather a doublon–hole continuum superimposed on the doublon satellite. The filter-operator analysis in section 3.7 and further arguments given below indeed support this interpretation.

Compared to the three-hole spectrum, 'T' in figure 3 has smaller spectral weight, but the same shape. We would like to stress that the two peaks belonging to 'T' are simply a consequence of the van Hove singularities in one-dimension, separated by about $16{t}^{2}/U\approx 2.67t$ for $U=6t$, and should not be mistaken for separate resonances. Hence, they will not be observed for higher-dimensional lattices.

The interpretation of 'T' as a doublon–hole continuum also explains that it is located at approximately U below the barycenter of the three-hole continuum. The latter is given by ${\omega }_{0}=-6t$ for n = 2. With decreasing filling the support of the three-hole continuum shrinks, and so does its barycenter, but at a faster rate than the two-hole continuum, so that the doublon–hole continuum 'T' eventually merges with the doublon satellite for fillings approaching half-filling.

A stable, repulsively bound triplon forms in the presence of an additional repulsive nearest-neighbor Coulomb interaction V. This situation is shown in figure 7. Starting from the doublon–hole continuum at $U=6t$ and V = 0, and switching on V leads to the emergence of two satellites splitting off for sufficiently strong V. Both have the same shape as the non-interacting density of states ${\rho }_{0}(x)$ and are separated by about $2V$ from the continuum. The presence of two satellites rather than one is due to the fact that a triplon has an internal degree of freedom: on two sites, the three-hole states ${(1,0)}^{T}\equiv {c}_{1\uparrow }^{\dagger }| {\rm{vac.}}\rangle$ and ${(0,1)}^{T}\equiv {c}_{2\uparrow }^{\dagger }| {\rm{vac.}}\rangle$ form two configurations. When coupled by the Hamiltonian

$$\begin{eqnarray}{H}_{2}=\left(\begin{array}{cc}U+2V & -t\\ -t & U+2V\end{array}\right),\end{eqnarray} \tag{ 25 }$$

they result in a pair of bonding/antibonding eigenstates at energies ${E}_{\pm }=U+2V\pm t$. Note that with H₂, we count the interaction between holes rather than electrons. The energy splitting of $2t$ very well explains the energy difference between the positions of the two satellites in the spectra in figure 7. Their widths are different, but become equal in the strong-coupling limit $U,V\gg t$ and are then given by $8{t}^{2}/(U+2V)$.

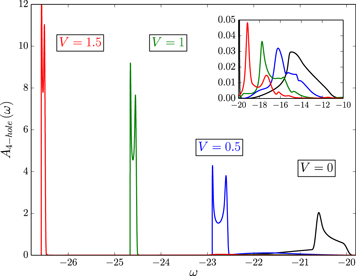
Zoom In Zoom Out Reset image size

Figure 8 shows the emergence of the two triplon satellites in the two-hole spectrum at n = 1.8 as obtained by DMRG. With $V\gt 0$, we find a much stronger growth of the entanglement entropy during the Chebyshev iteration. This is to be expected, as the model becomes non-integrable [55]. These spectra have therefore been calculated at a moderate energy resolution $\delta E=0.4t$. For V = 3, for example, the MPS bond dimension at this point already exceeds 6200.

Zoom In Zoom Out Reset image size

For V = 0, we find the dominating doublon satellite around $\omega \approx -10t$ and the two peaks of the doublon–hole continuum at higher binding energies, separated by about $16{t}^{2}/U\approx 2.67t$. One is located at $\omega \approx -13.1t$, while to other one is next to the intense van Hove singularity of the doublon structure at $\omega \approx -10.4t$, and barely distinguishable from it. It requires a high-resolution calculation to uncover this feature ($\delta E=0.04t$, the purple curve in figure 8). For $V\gt 0$, the double-peak structure of the triplon appears, with a separation of $2t$ and shifting by about $2V$ with increasing V, as in the case of the three-hole spectrum (figure 7). The doublon satellite, on the other hand, shows a considerable loss of spectral weight, but has a basically unchanged position when increasing V. In addition, we observe another resonance emerging out of the band-like part at $\omega \approx -4t-V$, which we can identify as two neighboring holes repulsively bound by V as a dimer.

The available resolution does not allow us to determine the fine structure of the triplon peaks. The linear-prediction technique [30, 43, 44], which is commonly used to enhance the resolution, has not provided us with additional spectral information in this case. Instead, we go to an even higher filling, n = 1.98, where an exact calculation is still feasible for a fairly large system. The result for L = 100 and $\delta E=0.01$ is shown in the inset of figure 8. We observe that while the first of the triplon peaks appears right away, the second one only rises above the continuum when V exceeds a critical value of ${V}_{{\rm{c}}}\approx 1.3$. Note that the shape of the former markedly differs from the free density of states, indicating that in contrast to the three-hole spectral function (figure 7), the triplon in ${A}_{2-\mathrm{hole},\sigma }(\omega )$ does not become stable in the whole Brillouin zone.

The two-hole spectrum of the half-filled Hubbard model (see figure 3, lowest panel) displays a broad peak 'Q' centered around $\omega \approx -7.4t$.

A two-hole excitation requires a double occupancy at a site i in the ground state $| 0,N\rangle$. For strong U and N = L, a corresponding configuration is generated by a virtual second-order hopping process, which at the same time favors antiferromagnetic spin correlations. This is the famous Anderson super-exchange [56]. Starting from this initial-state configuration, the resulting configuration contributing to the $N-2$-electron final state $| n,N-2\rangle$ must therefore contain two nearest-neighboring empty sites, i.e., two neighboring doublons (see the sketch given in figure 9). One may ask whether these bind to form a heavier 'quadruplon'.

Zoom In Zoom Out Reset image size

Before addressing this question quantitatively, let us attempt a simple argument favoring an interpretation of 'Q' as a bound quadruplon opposed to two independently propagating doublons: Close to half-filling the low-energy states of the system exhibit strong antiferromagnetic correlations. Hence, there are two missing magnetic bonds associated with a single hole propagating in this antiferromagnetic background corresponding to an excitation energy $2J$. Consequently, letting the two neighboring doublons, i.e., the two neighboring holes in the final state (figure 9(b)) dissociate and propagate independently costs $4J$ while forming a compound quadruplon requires $3J$ only. In the strong J-limit of the t–J model, equation (22), where the loss of kinetic energy upon quadruplon formation can be neglected, this argument [35] is strict. For weak J, related to the present case of the Hubbard model, it serves as a simple picture for the binding mechanism only.

A simple inspection of the presence of a binding energy can be done using the position of 'Q': a two-doublon continuum would be expected at twice the energetic center of the doublon satellite, an additional binding energy would mean a shift from that position. Looking at the closest dataset to half-filling ($n=62/60$ in figure 3), we do not see such a shift within plotting accuracy, the 'Q' peak at $\omega \approx 9.8$ coincides with the expected continuum center. Going to higher fillings, however, we find a shift that increases roughly linearly with n (from ${\rm{\Delta }}\omega \approx 0.1$ at n = 1.2 to ${\rm{\Delta }}\omega \approx 0.4$ at n = 1.6) towards lower binding energies, i.e. the doublons seem to bind attractively as the filling increases.

For $n\to 2$ the phase space for quadruplon formation shrinks to zero. However, we can address the quadruplon formation in the final state and carry out a similar analysis as in section 3.5 by calculating the following four-hole spectral function

$$\begin{eqnarray}{A}_{4-\mathrm{hole}}(\omega ) & = & \displaystyle \sum _{n}{| \langle n,N-4| {c}_{i\uparrow }{c}_{i\downarrow }{c}_{i+1\uparrow }{c}_{i+1\downarrow }| 0,N\rangle | }^{2}\\ & & \times \delta (\omega +4\mu -({E}_{0}^{(N)}-{E}_{n}^{(N-4)}))\end{eqnarray} \tag{ 26 }$$

for the completely filled band. The result is shown in figure 10.

Zoom In Zoom Out Reset image size

For U = 0, the spectrum consists of a four-hole continuum at low binding energies; its support is given by $4W=16t$. For strong U, this continuum has extremely small spectral weight. Some weight has been transferred to an extended structure at intermediate excitation energies around $\omega =-8t-U$ which we identify as the one-doublon-two-hole continuum. Most of the weight, however, is taken by the correlation satellite located at $\omega \approx -8t-2U$ which corresponds to final states with two doublons. Notably, its shape does not resemble the self-convolution of a doublon satellite (see figure 1), as one would expect for a doublon–doublon continuum.

This is in fact corroborated by the analysis of an effective model [14, 57], valid for strong U in the subspace with a fixed number of doublons, but no singly occupied sites:

$$\begin{eqnarray}{H}_{{\rm{eff}}} & = & \displaystyle \frac{J}{2}\displaystyle \sum _{\langle {ij}\rangle }({d}_{i}^{\dagger }{d}_{j}+{\rm{h.c.}})+ & (J+U)\displaystyle \sum _{i}{n}_{i}^{d}-J\displaystyle \sum _{\langle {ij}\rangle }{n}_{i}^{d}{n}_{j}^{d}.\end{eqnarray} \tag{ 27 }$$

The model describes inherently stable bosons with the creation operator ${d}_{i}^{\dagger }={c}_{i\uparrow }^{\dagger }{c}_{i\downarrow }^{\dagger }$ and a hard-core constraint ${({d}_{i}^{\dagger })}^{2}=0$ enforcing that any site is at most singly occupied with a single boson. Recall that throughout the paper, a doublon refers to a pair of holes rather than particles, and hence a doublon at site i corresponds to a hole ${n}_{i}^{d}=0$, where ${n}_{i}^{d}={d}_{i}^{\dagger }{d}_{i}$ is the boson occupation-number operator. The effective model includes a hopping term with amplitude $J/2=2{t}^{2}/U$ and a nearest-neighbor density–density interaction of strength J, thus twice the hopping amplitude, but only half the bandwidth $2J$. Note that this effective doublon–doublon interaction is attractive.

Our four-hole problem now becomes a two-hole problem in the effective model, equation (27), and can be solved in much the same way as the two-hole problem in the Cini–Sawatzky case, see [58] and section 3.1. Separating the relative from the center-of-mass motion, the eigenvalues can be calculated for rather large systems. One does indeed observe a split-off resonance for certain values of the wave vector k, corresponding to a bound quadruplon. However, due to the small interaction strength J, the bound state is energetically positioned within the doublon–doublon continuum.

In order to demonstrate this, rather than showing just the eigenvalues, we calculate the k-resolved two-doublon spectral function within the effective model:

$$\begin{eqnarray}&&{A}_{2-\mathrm{doublon}}(\omega ,k)=\displaystyle \frac{1}{L}\displaystyle \sum _{n}{\left|\langle n,{N}_{d}-2| \displaystyle \sum _{i}{{\rm{e}}}^{-{\rm{i}}{{kR}}_{i}}{d}_{i}{d}_{i+1}| 0,{N}_{d}\rangle \right|}^{2}\delta (\omega -({E}_{0}^{({N}_{d}-2)}-{E}_{n}^{({N}_{d}-2)})).\end{eqnarray} \tag{ 28 }$$

Note that it is for simplicity defined such that the lowest binding energy is $\omega =0$. Figure 11 shows the result of a calculation for ${N}_{d}=L=1000$ and $J=2t/3$ corresponding to filling n = 2 and interaction $U=6t$ in the original model. The two-doublon spectrum corresponds to the satellite around $\omega =-8t-2U-2J\approx -21.3t$ in figure 10. The support is given by ${\rm{\Delta }}\omega =8t/3\approx 2.67t$, though with very little weight on the high-binding-energy side. This is the expected value for two independent doublons: ${\rm{\Delta }}\omega =2\times 4\times J/2$.

Zoom In Zoom Out Reset image size

The k-resolution uncovers that the continuum actually has very small spectral weight and that the spectrum is in fact dominated by the intense quadruplon peak. Around the Brillouin-zone center the quadruplon is a resonance with a finite width, but still its weight dominates the whole energy range. For $| k| \gtrsim 3\pi /4$, it is fully split off from the continuum and has zero intrinsic width (the width is due to the finite $\delta E$ only). We conclude that the quadruplon excitation represents a stable compound object formed by two bound doublons when its wave vector is close to the zone boundary, while it is a well-defined resonance with finite lifetime around the zone center.

The stability of the quadruplon can be explained by a phase-space argument: for a state from the two-doublon continuum, the hard-core constraint is not effective in the thermodynamic limit. Hence, the total energy of two doublons with wave vectors p and k − p is obtained as $J\mathrm{cos}(p)+J\mathrm{cos}(k-p)$. Right at $k=\pm \pi$, this adds up to zero, so that a bound quadruplon of arbitrary energy $\omega \ne 0$ and wave vector $k=\pm \pi$ cannot decay. Note that the quadruplon branches split off from the continuum on the low-binding-energy side, as the quadruplon is bound by an attractive interaction of strength J, see equation (27). Indeed, the quadruplon binding energy at $k=\pm \pi$ is given by $J=2{t}^{2}/3U\approx 0.67t$ [58].

The same physics is found when considering the k-resolved four-hole spectral function in the full model:

$$\begin{eqnarray}&&{A}_{4-\mathrm{hole}}(\omega ,k)= \\ &&\displaystyle \frac{1}{L}\displaystyle \sum _{n}{\left|\langle n,N-4| \displaystyle \sum _{i}{{\rm{e}}}^{-{\rm{i}}{{kR}}_{i}}{c}_{i\uparrow }{c}_{i\downarrow }{c}_{i+1\uparrow }{c}_{i+1\downarrow }| 0,N\rangle \right|}^{2}\delta (\omega +4\mu -({E}_{0}^{(N)}-{E}_{n}^{(N-4)})).\end{eqnarray} \tag{ 29 }$$

This is shown in figure 12 for $U=6t$. Due to the now allowed singly occupied sites and a finite U, the one-doublon-two-hole continuum around $\omega \approx \omega =-8t-U$ acquires some spectral weight. This corresponds to final states where one of the doublons has decayed. Most of the spectral weight, however, is taken by the quadruplon resonance or bound state at higher binding energies. For the quadruplon binding energy at $k=\pm \pi$, we obtain about $0.58t$ due to the moderate strength of $U=6t$.

Zoom In Zoom Out Reset image size

At this point, we briefly note that the quadruplon is stabilized in the entire Brillouin zone by a sufficiently strong nearest-neighbor Coulomb interaction $V\gt 0$, very similar to the case of the triplon excitation discussed in section 3.5. Figure 13 shows the (local) four-hole spectrum for $U=6t$ and different V. Here, the quadruplon satellite, with a shape approaching the shape of the free density of states for strong V, is fully split off from the (very weak) two-doublon continuum and shows up on its high-binding-energy side since the interaction is repulsive. With increasing V, the quadruplon peak shifts with the additional binding energy $4V$.

Zoom In Zoom Out Reset image size

Next, we continue to tackle the question of whether there is a stable bound quadruplon in the two-hole spectrum. First, we note that the structure 'Q' in ${A}_{2-\mathrm{hole}}(\omega )$ (see figure 3) continuously connects to the quadruplon peak analyzed with ${A}_{4-\mathrm{hole}}(\omega )$. This is demonstrated in appendix B where the (local) four-hole spectrum is presented in the entire filling range $1\leqslant n\leqslant 2$.

Hence, the question to be answered is the following: Do the two doublons in the final states contributing to 'Q' for fillings $n\lt 2$ bind and form a compound object, i.e., is there an enhanced probability to find the doublons at neighboring sites? Above we have already given an argument relying on the energy shift of 'Q' with respect to the expected position of the two-doublon continuum. However, a more direct analysis should be possible as the numerical approach is based on the many-body wave function which, in principle, contains all information on the system. One should therefore be able to extract specific information on the final states within a given frequency range. An implementation of this idea within the Chebyshev expansion method requires a new technique as described below.

To extract specific information on the states contributing to the two-hole spectrum at a given frequency ω, we proceed in the following way: first, we define a state $| {\rm{\Psi }}(\omega )\rangle$ as the sum over the complete set of energy eigenstates weighted by the matrix element of the transition operator:

$$\begin{eqnarray}&&| {\rm{\Psi }}(\omega )\rangle =\displaystyle \sum _{m}\langle m| {c}_{i\uparrow }{c}_{i\downarrow }| 0\rangle \;\delta (\omega -({E}_{0}-{E}_{m}))| m\rangle .\end{eqnarray} \tag{ 30 }$$

$| {\rm{\Psi }}(\omega )\rangle$ is constructed to represent a typical final state contributing to the spectrum at frequency ω. Note that it is coincidentally identical to the 'correction vector'

$$\begin{eqnarray}&&| {\rm{\Psi }}(\omega )\rangle =-\displaystyle \frac{1}{\pi }{\rm{Im}}\displaystyle \frac{1}{\omega +{\rm{i}}{0}^{+}-({E}_{0}-H)}{c}_{i\uparrow }{c}_{i\downarrow }| 0\rangle ,\end{eqnarray} \tag{ 31 }$$

which is employed within dynamical DMRG [36] to calculate the spectral function via ${A}_{2-\mathrm{hole}}(\omega )=\langle 0| {c}_{i\downarrow }^{\dagger }{c}_{i\uparrow }^{\dagger }| {\rm{\Psi }}(\omega )\rangle$.

Here, we employ it in a different way, choosing a Hermitian (but otherwise in principle arbitrary) 'filter operator' F and calculate the following expectation value:

$$\begin{eqnarray}&&\langle {\rm{\Psi }}(\omega )| F| {\rm{\Psi }}(\omega )\rangle =\displaystyle \sum _{{mn}}\langle 0| {c}_{i\downarrow }^{\dagger }{c}_{i\uparrow }^{\dagger }| m\rangle \langle m| F| n\rangle \langle n| {c}_{i\uparrow }{c}_{i\downarrow }| 0\rangle \delta (\omega -({E}_{0}-{E}_{m}))\delta (\omega -({E}_{0}-{E}_{n})).\end{eqnarray} \tag{ 32 }$$

This constitutes a 'filtered' two-hole spectral function which we call ${A}_{2-\mathrm{hole}}[F](\omega )$. The additional weight factors $\langle m| F| n\rangle$ give us some characterization of the eigenstates involved, depending on the choice of F. The normal spectrum is obviously recovered for F = 1. This quantity is numerically accessible as the diagonal part ($\omega =x=y$) of the two-dimensional Chebyshev expansion defined by

$$\begin{eqnarray}&&{A}_{2-\mathrm{hole}}[F](x,y)=\displaystyle \sum _{{mn}}\langle 0| {c}_{i\downarrow }^{\dagger }{c}_{i\uparrow }^{\dagger }| n\rangle \langle m| F| n\rangle \langle n| {c}_{i\uparrow }{c}_{i\downarrow }| 0\rangle \delta (x-({x}_{0}-{x}_{n}))\delta (y-({x}_{0}-{x}_{m})),\end{eqnarray} \tag{ 33 }$$

where the moments are given by

$$\begin{eqnarray}&&{\mu }_{{mn}}=\displaystyle \sum _{{mn}}\langle 0| {c}_{i\downarrow }^{\dagger }{c}_{i\uparrow }^{\dagger }\;{T}_{m}(\tilde{H})\;F\;{T}_{n}(\tilde{H})\;{c}_{i\uparrow }{c}_{i\downarrow }| 0\rangle \end{eqnarray} \tag{ 34 }$$

in terms of the Chebyshev polynomials of the rescaled Hamiltonian, see section 2.

To convince ourselves that this method works, we first consider the well-understood limit of the completely filled band n = 2. We define an operator h_i which projects out states with an empty site i as

$$\begin{eqnarray}&&{h}_{i}=(1-{n}_{i\uparrow })(1-{n}_{i\downarrow }),\end{eqnarray} \tag{ 35 }$$

and an operator s_i, projecting out states with single occupancy at i:

$$\begin{eqnarray}&&{s}_{i}=(1-{n}_{i\uparrow }{n}_{i\downarrow })(1-{h}_{i})={n}_{i\uparrow }+{n}_{i\downarrow }-2{n}_{i\uparrow }{n}_{i\downarrow }.\end{eqnarray} \tag{ 36 }$$

With this we can use $F=\frac{1}{L}{\sum }_{i}{h}_{i}$ to filter out states characterized by doublons, and $F=\frac{1}{L}{\sum }_{i}{s}_{i}$ to filter out states characterized by the absence of doublons, but the presence of single holes.

Results for $U=6t$ are shown in figure 14. We do indeed observe that the spectral function obtained with the former filter has support at the doublon satellite only, while the support of the latter coincides with spectral range of the band-like part and of the satellite. That the spectral function filtering out final states with singly occupied sites has finite weight at the doublon satellite reflects that doublon propagation in fact involves intermediate configurations with singly occupied sites.

Zoom In Zoom Out Reset image size

Next we test the triplon case. Recall that the two-hole spectral function is computed at the central site of the chain, i.e., we take $i=L/2$ for the transition operator ${c}_{i\uparrow }{c}_{i\downarrow }$. To look for triplons, we can thus choose local filters and take $F={h}_{L/2}{s}_{L/2+\delta }$ at different distances δ. An enhanced weight at $\delta =1$ would indicate that the doublon and the additional hole bind and form a stable triplon.

The result of calculations for n = 1.8 is shown in figure 15. We do indeed see that the case $\delta =1$ does not look any more special than $\delta =2$, $\delta =3$ or $\delta =L/2$. All choices roughly reproduce the shape of the two-hole spectral function and are barely distinguishable in the range of the peak at $\omega \approx -13.1t$, earlier identified as the triplon structure. This corroborates our previous result that doublon and hole do not bind. On the other hand, a stable triplon is formed for a nearest-neighbor interaction V = 1. This is indeed supported by the filter-operator technique: for V = 1 (see inset of figure 15) the case $\delta =1$ is in fact very different as compared to $\delta \ne 1$: the weight of the filtered spectrum is strongly enhanced at frequencies around $\omega =-14.4t$, where the peak of the bound triplon is located (see figure 8).

Zoom In Zoom Out Reset image size

Finally, to investigate the quadruplon, we consider the filling $n=62/60$ right above half-filling. The quadruplon peak is located at $\omega \approx -9.8t$ below the doublon structure with barycenter at $\omega \approx -6t$, see figure 3. We have computed filtered spectra using $F={h}_{L/2}{h}_{L/2+\delta }$.

Results are shown in figure 16. In this case, a filter with $\delta =1$ produces a strong signal at the quadruplon position even for V = 0, while the spectra for larger distances $\delta \ne 1$ are again close to each other and roughly coincide with the original spectral function. This is a clear indication that there is a bound quadruplon, the contribution of which dominates the two-hole spectrum ${A}_{2-\mathrm{hole}}(\omega )$, as compared to the doublon–doublon continuum.

Zoom In Zoom Out Reset image size

Let us return to the doublon. As has been discussed in section 3.3, a stable excitation with infinite lifetime is found in the simple n = 2 limit and explained as a repulsively bound pair of holes. This interpretation breaks down for fillings close to half-filling, where the two-hole excitation propagates through a background of singly occupied sites with antiferromagnetic correlations. We are thus left with the question whether there is a stable doublon for fillings $n\lt 2$, and close to half-filling in particular.

The U-dependence of the doublon lifetime has been addressed in a number of previous theoretical as well as experimental studies [10–14, 57, 59], starting from the concept of repulsive binding. Here, we would like to emphasize that the k-resolution of the local two-hole excitation adds an important new view to this problem. For the case of periodic boundary conditions, the k-resolved two-hole spectral function is defined as:

$$\begin{eqnarray}{A}_{2-\mathrm{hole}}(\omega ,k) & = & \displaystyle \frac{1}{L}\displaystyle \sum _{n}{\left|\langle n,N-2| \displaystyle \sum _{i}{{\rm{e}}}^{-{\rm{i}}{{kR}}_{i}}{c}_{i\uparrow }{c}_{i\downarrow }| 0,N\rangle \right|}^{2}\\ & & \times \delta (\omega +2\mu -({E}_{0}^{(N)}-{E}_{n}^{(N-2)})).\end{eqnarray} \tag{ 37 }$$

Exploiting translational symmetry, it is straightforward to show that k-summation yields

$$\begin{eqnarray}&&{A}_{2-\mathrm{hole}}(\omega )=\displaystyle \frac{1}{L}\displaystyle \sum _{k}{A}_{2-\mathrm{hole}}(\omega ,k).\end{eqnarray} \tag{ 38 }$$

Hence, with ${A}_{2-\mathrm{hole}}(\omega ,k)$, one actually decomposes the local two-hole excitation into a coherent linear superposition of k-dependent two-hole excitations:

$$\begin{eqnarray}&&{c}_{i\uparrow }{c}_{i\downarrow }| 0,N\rangle =\displaystyle \sum _{k}{d}_{k}| 0,N\rangle ,\end{eqnarray} \tag{ 39 }$$

where ${d}_{k}={L}^{-1}{\sum }_{i}{{\rm{e}}}^{-{\rm{i}}{{kR}}_{i}}{c}_{i\uparrow }{c}_{i\downarrow }={L}^{-1}{\sum }_{p}{c}_{p\uparrow }{c}_{k-p\downarrow }$ with ${c}_{k\sigma }={L}^{-1/2}{\sum }_{i}{{\rm{e}}}^{-{\rm{i}}{{kR}}_{i}}{c}_{i\sigma }$. The important observation is that the state ${d}_{k}| 0,N\rangle$ has a strongly k-dependent lifetime. At the zone boundary $k=\pi$, the lifetime is even infinite.

This can be verified numerically and understood analytically. Let us first discuss the numerical results. Equation (37) can be used to approximate the two-hole spectrum with a calculation for a system with open boundaries. In this case, the k-summation of ${A}_{2-\mathrm{hole}}(\omega ,k)$ (equation (38)) yields the local spectrum, but averaged over all sites, rather than the local spectral function at the central site i, as defined in equation (5). For a system with size L = 60, however, the approximation is already excellent. Note that this can also be thought of as carrying out a Fourier transform with two momenta, ${A}_{2-\mathrm{hole}}(\omega ,k,{k}^{\prime })$, but then only looking at the diagonal component with $k={k}^{\prime }$: ${A}_{2-\mathrm{hole}}(\omega ,k)\equiv {A}_{2-\mathrm{hole}}(\omega ,k,k)$.

Figure 17 shows the k-resolved spectrum for n = 1.8 and $U=6t$. The band-like part extends from $\omega =0$ to $\omega \approx -8t$ with most of the spectral weight at low binding energies and a ridge-like structure around k = 0. Its overall spectral weight, however, is very small compared to the weight of the doublon satellite, which is centered around $\omega \approx -10t$. Interestingly, one finds that the doublon satellite is not broadened at all for $k=\pm \pi$. In fact, the structure at $k=\pm \pi$ should be interpreted as a δ-peak at frequency $\omega ={\omega }_{0}(\pi )\approx -9.25t$. Note that on the logarithmic scale, there are seemingly sidebands visible close to ${\omega }_{0}(\pi )$ and $k=\pm \pi$. These are, however, simply the numerical artifact of Gibbs oscillations. As shown below, the position of the δ-peak is precisely given by ${\omega }_{0}(\pi )=U-2\mu \approx -9.25t$, where the value of μ is obtained from the ground-state calculation (equation (7)). When $| k| \lt \pi$, the satellite acquires some finite width, i.e., the doublon transmutes from a stable bound object into a resonance. Its lifetime is shortest around k = 0. This is opposed to the simple n = 2 limit, where the doublon is stable in the entire Brillouin zone.

Zoom In Zoom Out Reset image size

The situation at a filling n = 1.1 is very similar. Results are shown figure 18. Here, the k-resolved two-hole spectrum consists of an intense doublon satellite (centered around $\omega \approx -5t$) and the quadruplon structure (around $\omega \approx -10t$), as well as a band-like part with non-zero, but extremely low weight close to $\omega =0$ which is not visible in the figure. Referring to the results obtained by means of the filter-operator technique in section 3.7, we interpret the quadruplon structure as an object composed of two doublons but with a finite lifetime, i.e., a resonance. Most of its weight is located close to k = 0. It is tempting to assume that the quadruplon is entirely stable at $k=\pi$, similar to the four-hole spectrum case (figure 12), but the whole spectral weight at the zone boundary is instead taken by the doublon satellite. We have already seen a similar effect in the case of the triplon: in the three-hole spectral function for n = 2 (figure 7), it clearly has a different dispersion from the two-hole spectral function for $n\lt 2$ (the inset of figure 8), while the energetic positions follow the same rules.

Zoom In Zoom Out Reset image size

Turning to the doublon in figure 18, we observe that it has infinite lifetime at $k=\pm \pi$ again, but now also displays a distinct 'shadow' around k = 0. For n = 1.1 we find $2\mu =9.25$, and thus expect the doublon at energy ${\omega }_{0}(\pi )=U-2\mu \approx -3.25t$. This perfectly fits with the position that can be read off from figure 18.

The stability of the doublon at the zone edges can be understood analytically by referring to the 'hidden' charge-SU(2) symmetry of the Hubbard model [60, 61]. We define

$$\begin{eqnarray}&&\eta =\displaystyle \sum _{i}{(-1)}^{i}{c}_{i\uparrow }{c}_{i\downarrow }.\end{eqnarray} \tag{ 40 }$$

For the model considered here, and in general for a Hubbard model with V = 0 on a bipartite lattice in D dimensions, one easily verifies that η is an eigenoperator of H and of the total particle-number operator $\hat{N}$:

$$\begin{eqnarray}&&[\eta ,H]=U\eta ,\quad [\eta ,\hat{N}]=2\eta .\end{eqnarray} \tag{ 41 }$$

η is related to the total isospin ${\boldsymbol{T}}$, the components of which are given by ${T}_{x}=(\eta +{\eta }^{\dagger })/2$, ${T}_{y}=(\eta -{\eta }^{\dagger })/(2i)$ and ${T}_{z}=(L-\hat{N})/2$, and represent the generators of a global charge-SU(2) symmetry of the model at half-filling: $[{\boldsymbol{T}},H-\mu \hat{N}]=0$ for $\mu =U/2$. Starting from the total spin ${\boldsymbol{S}}$, which generates the standard spin-SU(2) group, the isospin is obtained by a spin-asymmetric and staggered particle–hole (Shiba) transformation ${U}_{{\rm{sh}}}$ with ${U}_{{\rm{sh}}}^{\dagger }{c}_{i\uparrow }{U}_{{\rm{sh}}}={(-1)}^{i}{c}_{i\uparrow }^{\dagger }$. We have ${U}_{{\rm{sh}}}^{\dagger }{\boldsymbol{S}}{U}_{{\rm{sh}}}={\boldsymbol{T}}$.

At half-filling (N = L) the ground state $| 0,N\rangle$ is a non-degenerate total spin singlet. This implies immediately that $| 0,N\rangle$ is a total isospin singlet as well. Hence, we have $\eta | 0,N=L\rangle =0$. Since ${d}_{k=\pi }=\eta /L$ for $k=\pi$, the transition operator in the Lehmann representation of the k-resolved two-hole spectral function, equation (37), is just proportional to η. For the case of half-filling this implies

$$\begin{eqnarray}&&{A}_{2-\mathrm{hole}}(\omega ,k=\pi )=0\end{eqnarray} \tag{ 42 }$$

for all excitation energies ω. This is consistent with the DMRG calculations which predict the doublon satellite to vanish for n = 1, even in the entire Brillouin zone (see figure 3).

Off half-filling, the chemical potential $\mu \ne U/2$ explicitly breaks the charge-SU(2) symmetry and produces a massive collective mode showing up as a single δ-peak in the two-hole spectrum at wave vector $k=\pi$ (the same holds for $k=-\pi$). This can be inferred from equation (41). Namely, it is easy to see that, for arbitrary N, the state $\eta | 0,N\rangle$ is an exact eigenstate of H with energy ${E}_{0}^{(N)}-U$. Inserting this into equation (37), yields

$$\begin{eqnarray}&&{A}_{2-\mathrm{hole}}(\omega ,k=\pi )=\alpha \ \delta (\omega +2\mu -U).\end{eqnarray} \tag{ 43 }$$

This explains the observed position ${\omega }_{0}(\pi )=U-2\mu$.

Integrating the k-resolved spectrum, equation (37), over ω, yields the total weight at a given k:

$$\begin{eqnarray}&&\alpha (k)=\displaystyle \frac{1}{L}\displaystyle \sum _{{ij}}{{\rm{e}}}^{-{\rm{i}}k({R}_{i}-{R}_{j})}\langle 0,N| {c}_{j\downarrow }^{\dagger }{c}_{j\uparrow }^{\dagger }{c}_{i\uparrow }{c}_{i\downarrow }| 0,N\rangle .\end{eqnarray} \tag{ 44 }$$

This gives ${\sum }_{k}\alpha (k)={\sum }_{i}\langle {n}_{i\uparrow }{n}_{i\downarrow }\rangle$, consistent with the global sum rule equation (18). At $k=\pi$, as expressed by equation (43), the whole spectral weight condenses to $\alpha (\pi )$ at frequency $\omega =U-2\mu$. The weight of the mode at the zone boundary is then given by $\alpha ={L}^{-1}\langle 0,N| {\eta }^{\dagger }\eta | 0,N\rangle$, see equations (40) and (44), and can be expressed in terms of the isospin as follows:

$$\begin{eqnarray}&&\alpha =\displaystyle \frac{1}{L}\langle 0,N| ({{\boldsymbol{T}}}^{2}-{T}_{z}({T}_{z}+1))| 0,N\rangle .\end{eqnarray} \tag{ 45 }$$

Off half-filling, it is instructive to decompose the Hamiltonian ${ \mathcal H }\equiv H-\mu \hat{N}$ into ${ \mathcal H }={{ \mathcal H }}_{0}-(U-2\mu ){T}_{z}+{\rm{const.}}$ where ${{ \mathcal H }}_{0}=H-(U/2)\hat{N}$ is the charge-SU(2) symmetric part ($[{\boldsymbol{T}},{{ \mathcal H }}_{0}]=0$) and where the second term represents a homogeneous field coupling to the z-component of ${\boldsymbol{T}}$. The field explicitly breaks the charge-SU(2) symmetry and isospin-polarizes the ground state. We still have $[{{\boldsymbol{T}}}^{2},{ \mathcal H }]=0$ and $[{T}_{z},{ \mathcal H }]=0$ (but $[\eta ,{ \mathcal H }]\ne 0$), i.e., like in a ferromagnet there are no fluctuations of T_z and the ground state is characterized by the isospin quantum numbers $(T,{M}_{T})$ corresponding to $({{\boldsymbol{T}}}^{2},{T}_{z})$. For fillings above half-filling, we have $\mu \gt U/2$, and the field term leads to a state with the isospin pointing into $-z$-direction, i.e., ${M}_{T}=-T$. Using this in equation (45), we find

$$\begin{eqnarray}&&\alpha =-2{M}_{T}/L=(N-L)/L=n-1,\end{eqnarray} \tag{ 46 }$$

where we also used ${M}_{T}=(L-N)/2$. We conclude that the weight of the mode linearly increases from zero at half-filling to unity at n = 2. This explains the strong difference in the weights seen in the DMRG results (figures 17 and 18).

The same analysis can be done for the k-resolved two-particle spectrum and fillings $n\gt 1$. Here, however, the exact eigenstate ${\eta }^{\dagger }| 0,N\rangle$ would lead to a δ-peak at negative frequency $\omega ={\omega }_{0}(\pi )=U-2\mu \lt 0$ for $n\gt 1$ (which would contradict equations (6) and (7)) but the weight $\alpha ={L}^{-1}\langle \eta {\eta }^{\dagger }\rangle ={L}^{-1}\langle ({{\boldsymbol{T}}}^{2}-{T}_{z}({T}_{z}-1))\rangle$ vanishes exactly since ${M}_{T}=-T$. For fillings $n\lt 1$, the δ-peak in the two-particle spectrum shows up on the $\omega \gt 0$ side with a non-zero weight since ${M}_{T}=+T$ in this case—analogous to the two-hole spectrum for $n\gt 1$ and related to the latter by particle–hole transformation.

Physically, the collective mode describes the coherent propagation of a doublon with energy $U-2\mu$ through the lattice without any scattering, i.e., the final state with wave vector $k=\pi$ in the two-hole spectroscopy has infinite lifetime. This is enforced by the remaining isospin–rotation symmetry around the z-axis which protects the 'η-mode' at the zone edge from decay. Note that the η-mode only shows up off half-filling and is not bound to off-diagonal long-range order as has been discussed previously [60, 61]. For bipartite lattices of higher dimensions, the η-mode is found at the Brillouin-zone edges ${\boldsymbol{k}}=(\pm \pi ,\pm \pi ,...)$.