Dual trapped-ion quantum simulators: an alternative route towards exotic quantum magnets

Nowadays, the importance of the Ising model in the theory of statistical mechanics can be hardly exaggerated [1]. Nonetheless, early results proved the absence of spontaneous magnetization in the one-dimensional (1D) model and pointed to the lack of phase transitions also in higher dimensions [2], thus stimulating the appearance of other models to explain ferromagnetism [3]. The arguments against the existence of phase transitions in higher dimensions were proven wrong by subsequent efforts [1], such as the exact solution of the Ising model on a 2D square lattice [4], and eventually turned the Ising model into a paradigm of critical phenomena.

Moreover, the relevance of the Ising model goes far beyond the theory of thermal phase transitions. For instance, the partition function of the square-lattice Ising model, and thus its critical phenomena, can be related to the ground state of the 1D Ising model subjected to a transverse magnetic field that plays the role of the temperature [5]. This leads to a new kind of critical effects, i.e. quantum phase transitions [6], where the ground state of a system changes abruptly as a microscopic parameter controlling the quantum fluctuations is varied. Thanks to its exact solution [7], this quantum Ising model also plays a pivotal role in the theory of quantum criticality [6] and, despite its apparent over-simplified appearance, has turned out to be a faithful representation of certain magnetic materials [8].

The Ising model also occupies a privileged position in the theory of emergence in many-body systems [9]. In certain geometries, such as the triangular lattice [10], antiferromagnetic Ising interactions cannot be simultaneously minimized, an effect known as frustration. In the 3D pyrochlore lattice, this magnetic frustration resembles the ordering of protons in water ice [11], and inhibits the development of magnetic order even at very low temperatures. This leads to exotic emergent effects [13] that can be measured in these so-called spin-ice materials [12], constituting a hallmark in the physics of spin liquids. Moreover, if quantum fluctuations are introduced, the wisdom is that even more exotic properties survive at zero temperatures, leading to the elusive quantum spin liquids [14].

From this perspective, it is thus important to understand the interplay of frustration and quantum fluctuations in the Ising model. The standard approach to introduce quantum fluctuations on the vastly degenerate Ising ground state considers additional Heisenberg exchange couplings of tunable strength, which flip pairs of spins and lead to the so-called XXZ model [15]. However, this is not the unique possibility. For instance, one may introduce quantum fluctuations by a transverse field leading to frustrated quantum Ising models, which can also host quantum spin liquids in certain lattices [16]. As a starting point towards this goal, envisaged in this paper, it is useful to identify setups where the physics of simpler frustrated quantum Ising models can be explored experimentally.

In addition to frustration, interesting many-body effects may also arise as one departs from the standard scenario of pair-wise interactions, and considers multi-particle couplings. For instance, the partition function of a spin-ice Ising model that combines 2- and 4-body interactions in a square lattice [17] can be mapped onto the so-called eight-vertex model [18], which is a paradigm for critical phenomena in ice-type models. In contrast to the standard Ising model with pairwise interactions [4], this Ising model with multi-spin interactions presents some rather exotic properties, e.g. critical exponents vary continuously with the strength of the four-body interactions, thus connecting different universality classes. In addition to this example, we note that even more exotic phenomena occur when (i) quantum fluctuations or/and (ii) higher dimensions are also considered: (i) the combination of four-body Ising interactions with a transverse field in the square lattice can lead to phases with topological order [19]. (ii) Ising models on the cubic lattice with four-body interactions possess a local gauge symmetry that forbids the use of the standard local order parameters [20]. By introducing quantum fluctuations through a transverse field, such models yield a (3+1)-dimensional Ising gauge theory [21, 22] through the Euclidean generalization of the quantum-classical mapping [5].

From this perspective, it is important to understand the interplay of multi-spin interactions with quantum fluctuations, and its role in the emergence of exotic quantum magnets. A useful tool to reach this goal, again envisaged in this paper, would be an experimental setup where simple quantum Ising models with multi-spin interactions can be implemented.

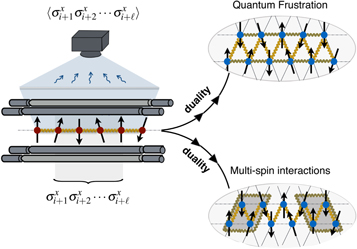
In this manuscript, we argue that current experiments of trapped-ion crystals can address the before-mentioned goals: we explicitly demonstrate that relevant instances of frustrated quantum Ising models, as well as exotic quantum Ising magnets with multi-spin interactions, can be implemented in such systems. For our proposal, we exploit a theoretical concept known as quantum dualities [21], which provides a mapping between different spin models. Broadly speaking, a dual map replaces the spin operators at the sites (vertices) of a lattice by analog operators acting on the bonds (links) between the vertices. Accordingly, duality can be used as a tool to switch between local and non-local models, which, as shown in this paper, facilitates the implementation of some Hamiltonians of interest in a trapped-ion setup (see figure 1).

Zoom In Zoom Out Reset image size

The paper is organized as follows. In section 2, we describe two possible strategies to simulate the required spin Hamiltonian in linear chains of trapped ions. In section 3, we review the notion of quantum duality, highlighting its potential for quantum simulators such as trapped-ion experiments, which allow for highly non-local measurements. This quantum duality is applied to propose quantum simulators of exotic quantum Ising magnets that incorporate the effects of frustration in section 4, or multi-spin interactions in section 5. Finally, we present our conclusions and outlook in section 6.

The ever-improving experimental control of certain quantum systems, especially in the realm of atomic, molecular, and optical physics, has reached such a level that it is now possible to devise systems that will behave according to specific quantum many-body models [23]. This synthetic quantum matter, usually known as a quantum simulator, provides an alternative route to address longstanding problems in condensed-matter physics, such as the interplay of frustration and quantum fluctuations mentioned above. Among the different experimental platforms available nowadays, small crystals of atomic ions confined by electromagnetic traps [24] have already proven to be quite flexible quantum simulators [25]. Let us briefly review the possibilities of trapped-ion quantum simulators in the context of frustrated and multi-spin quantum Ising models.

Following the seminal proposal to use the phonons of the ion crystal as mediators of spin–spin interactions [26] (for earlier related proposals see [27]), small-scale 1D quantum Ising magnets have been experimentally realized [28]. The most direct approaches to include frustration would require engineering 2D ion lattices with triangular motifs, either by considering Penning traps [26, 29] and micro-fabricated trap arrays in a surface electrode [26, 30], or by coping with the excess micro-motion associated with 2D lattices in common rf-traps [31]. A different approach, which has proven very fruitful [32], retains the 1D geometry of the crystals in linear Paul traps while exploiting the long-range character of the Ising interactions to induce frustration via next-to-nearest-neighbor couplings. In this work, we shall introduce an alternative method that also permits retaining the 1D lattices, but offers more flexibility by allowing full control of the range of frustration in the simulated spin models.

Regarding multi-spin interactions, there have been proposals [33] that generalize the above schemes [26] by considering nonlinear spin–phonon couplings that can induce 2- and 3-body Ising interactions at the expense of getting weaker spin–spin couplings with respect to the pair-wise scenario. Hence, synthesizing other multi-spin interactions, such as the mentioned four-body Ising couplings, will result in even weaker coupling strengths that question the possibility of an experimental observation. A different and very fruitful approach is to build stroboscopic quantum simulators by concatenating well-controlled unitaries [34]. For the particular unitaries available in trapped-ion setups, multi-spin interactions can be obtained by introducing simple sequences that involve auxiliary spins [35], as demonstrated in the experiments [36, 37]. In this work, we propose an alternative method to implement four-body interactions in an analog fashion, thus not limited by the accumulated error of the concatenated unitaries, but without the above-mentioned limitation on the coupling strengths.

The central idea of this work is to exploit the concept of quantum duality [21] to reach the desired quantum simulator of exotic Ising models with frustration, or multi-spin interactions, starting from a different Hamiltonian that is easier to realize in a certain setup. In particular, we will focus on the following physical Hamiltonian

$$\begin{eqnarray}&&{H}_{{\ell }\mathrm{XY}}=\displaystyle \sum _{i\lt j}({J}_{{ij}}^{x}{\sigma }_{i}^{x}{\sigma }_{j}^{x}+{J}_{{ij}}^{y}{\sigma }_{i}^{y}{\sigma }_{j}^{y})-\displaystyle \sum _{i}h{\sigma }_{i}^{x},\end{eqnarray} \tag{ 1 }$$

which shall be referred to as the longitudinal XY model (ℓXY), and is the one to be implemented in the ion-trap setup. Let us remark on the two unique features that make this synthetic magnet very different from real magnetic materials: (i) the exact number of spins can be experimentally controlled, (ii) the magnetization, or any other correlation function, can be measured locally. These two features, in combination with the quantum duality, will be crucial for the quantum simulation scheme hereby proposed.

Let us now describe the required ingredients to realize the above Hamiltonian (1), and postpone the duality connection to the desired Ising models to the following sections. We start by describing the standard approach in section 2.1, and then introduce an alternative that might be advantageous in section 2.2.

2.1. Spin model from a pair of spin-dependent forces

We consider a collection of laser-cooled atomic ions confined by a linear Paul trap, and forming a 1D Coulomb crystal with equilibrium positions ${{\bf{r}}}_{i}^{0}={z}_{i}^{0}{{\bf{e}}}_{z}$ for $i\in \{1,\cdots ,N\}$ [38] (see figure 1). The small vibrations around these equilibrium positions can be described in terms of three phonon branches, two radial $\alpha \in \{x,y\}$ and one longitudinal $\alpha =z$, namely

$$\begin{eqnarray}&&{H}_{{\rm{p}}}=\displaystyle \sum _{n,\alpha }{\omega }_{n,\alpha }{a}_{n,\alpha }^{\dagger }{a}_{n,\alpha }^{\phantom{\dagger }},\end{eqnarray} \tag{ 2 }$$

where we have introduced the bosonic operators ${a}_{n,\alpha }^{\dagger },{a}_{n,\alpha }^{\phantom{\dagger }}$ that create-annihilate a phonon associated to the normal-mode frequency ${\omega }_{n,\alpha }$, where $n\in \{1,\cdots ,N\}$.

The spin chain is formed by a pair of long-lived electronic levels from the energy-level structure of each particular ion, denoted as $| {\uparrow }_{i}\rangle ,| {\downarrow }_{i}\rangle$. This leads to a trivial spin Hamiltonian

$$\begin{eqnarray}&&{H}_{{\rm{s}}}=\displaystyle \sum _{i}\displaystyle \frac{{\omega }_{0}}{2}{\sigma }_{i}^{z},\end{eqnarray} \tag{ 3 }$$

where we have introduced the transition frequency ${\omega }_{0}$, and the Pauli spin operator ${\sigma }_{i}^{z}=| {\uparrow }_{i}\rangle \langle {\uparrow }_{i}| -| {\downarrow }_{i}\rangle \langle {\downarrow }_{i}|$. These spins can be coupled by phonon-mediated interactions, which require a particular form of spin–phonon coupling. One typically considers the so-called spin-dependent dipole forces, which follow from a moving optical lattice, and read as follows

$$\begin{eqnarray}&&{H}_{{\rm{sp}}}=\displaystyle \sum _{i,n}\displaystyle \sum _{\alpha ,\beta }{F}_{i,n}^{\alpha ,\beta }{\rm{\Delta }}{r}_{n,\alpha }{\sigma }_{i}^{\beta }{a}_{n,\alpha }^{\dagger }{{\rm{e}}}^{{\rm{i}}{{\rm{\Delta }}}_{n,\alpha ,\beta }t}+{\rm{h.c.}},\end{eqnarray} \tag{ 4 }$$

where we work in the interaction picture with respect to equations (2) and (3), and have neglected rapidly oscillating terms within a rotating wave approximation. Here, we have introduced the two remaining Pauli spin operators ${\sigma }_{i}^{x}=| {\uparrow }_{i}\rangle \langle {\downarrow }_{i}| +{\rm{h.c.,}}$ ${\sigma }_{i}^{y}={\rm{i}}| {\downarrow }_{i}\rangle \langle {\uparrow }_{i}| +{\rm{h.c.,}}$ the zero-point motion of the different vibrational modes ${\rm{\Delta }}{r}_{n,\alpha }$, the dipole light forces ${F}_{i,n}^{\alpha ,\beta }$, and their corresponding detunings ${{\rm{\Delta }}}_{n,\alpha ,\beta }$. We shall assume that a particular light force will only couple to a single vibrational axis, namely ${F}_{i,n}^{\alpha ,\beta }={F}_{i,n}^{\alpha }{\delta }_{\alpha ,\beta }$. Although the particular Pauli matrices of the state-dependent forces (4) coincide with the vibrational axis with this choice, we note that the direction of the spins depend on the phase of the dipole light forces rather than the spatial direction of the force.

If the trap frequencies are different ${\omega }_{x}\ne {\omega }_{y}\ne {\omega }_{z}$, such that their differences are much bigger than the far-detuned dipole forces $| {F}_{i,n}^{\alpha ,\beta }{\rm{\Delta }}{r}_{n,\alpha }| \ll | {{\rm{\Delta }}}_{n,\alpha ,\beta }| \ll | {\omega }_{\alpha }-{\omega }_{\beta }|$ [26], the phonons act as mere carriers of spin–spin interactions

$$\begin{eqnarray}&&{H}_{{\rm{eff}}}=\displaystyle \sum _{i\lt j}({J}_{{ij}}^{x}{\sigma }_{i}^{x}{\sigma }_{j}^{x}+{J}_{{ij}}^{y}{\sigma }_{i}^{y}{\sigma }_{j}^{y}+{J}_{{ij}}^{z}{\sigma }_{i}^{z}{\sigma }_{j}^{z}),\end{eqnarray} \tag{ 5 }$$

where the phonon-mediated spin–spin couplings

$$\begin{eqnarray}&&{J}_{{ij}}^{\alpha }=-\displaystyle \sum _{n}\displaystyle \frac{{F}_{i,n}^{\alpha }{({F}_{j,n}^{\alpha })}^{*}{\rm{\Delta }}{r}_{n,\alpha }^{2}}{{{\rm{\Delta }}}_{n,\alpha }}+{\rm{c.c.}},\end{eqnarray} \tag{ 6 }$$

have the standard second-order scaling ${ \mathcal O }({F}^{2}/{\rm{\Delta }})$, and thus correspond to virtual processes where a phonon is created and subsequently absorbed by a pair of distant spins in the chain.

We are interested in anisotropic XY models (1), and thus shall only consider dipole forces that couple to the two radial branches ${F}_{i,n}^{x}$, and ${F}_{i,n}^{y}$, such that the effective Hamiltonian (5) only contains XX and YY couplings. In addition, we shall consider a so-called longitudinal field h, which can be implemented by considering the standard carrier transitions [24] with the correct phase. The combination of these ingredients yields the desired ℓXY model of equation (1) with the corresponding spin–spin couplings in equation (6). As announced above, we shall not exploit the long-range nature of such couplings to engineer frustration [32]. Instead, we will consider the largest possible detunings, which lead to the smallest possible errors in the quantum simulation [26], and also yield a fast-decaying dipolar tail of the anti-ferromagnetic spin–spin interactions

$$\begin{eqnarray}&&{J}_{{ij}}^{\alpha }\approx \displaystyle \frac{{J}_{0}^{\alpha }}{| {z}_{i}^{0}-{z}_{j}^{0}{| }^{3}},\phantom{\rule{2ex}{0ex}}{J}_{0}^{\alpha }\gt 0,\phantom{\rule{2ex}{0ex}}\alpha \in \{x,y\}.\end{eqnarray} \tag{ 7 }$$

We thus obtain a dipolar version of the famous XY model [39], subjected to an additional longitudinal field.

In order to attain such a dipolar decay of interactions, the detuning Δ of the state-dependent forces must be quite large, which could in principle weaken the spin–spin couplings ${F}^{2}/{\rm{\Delta }}$. However, this problem can be overcome by simultaneously increasing laser intensities such that the ratio $F/{\rm{\Delta }}$ remains fixed. Although current experiments optimize the parameters to maximize the dipole force while minimizing the residual Raman scattering given the available laser power, and still do not allow for such a dipolar regime, we believe that there is no fundamental limitation that impedes reaching this regime in the future provided that more powerful laser sources become available. In any case, it is also important to study how the results to be presented below would get modified for the smaller detunings of current experiments, which have demonstrated that a power law decay in the spin–spin interactions ${J}_{{ij}}^{\alpha }\approx {J}_{0}^{\alpha }/| {z}_{i}^{0}-{z}_{j}^{0}{| }^{k}$ with exponents $k\lesssim 2$, is a sensible approximation for small-enough ion chains [41], although it must be modified in the thermodynamic limit [42].

2.2. Spin model from a single spin-dependent force

Let us note that, so far, there has not been any experimental realization of a spin model exploiting simultaneously two phonon branches of a trapped-ion crystal. Instead, the dynamics of excitations in the isotropic limit of the XY model has been explored by considering a single Ising model, and thus a single phonon branch to mediate the interactions, subjected to an additional very strong transverse field [40, 41]. Unfortunately, this isotropic limit leads to ${J}_{{ij}}^{x}={J}_{{ij}}^{y}$ in the above Hamiltonian (1). As will become apparent in the following sections, this would limit its interest as a simulator of exotic quantum magnets under the duality transformation. We now introduce a scheme to modify the implementation of [40, 41] and obtain a fully tunable XY model in a longitudinal field by exploiting a single phonon branch.

Let us consider the Ising model in a longitudinal field, which arises from considering a spin-dependent dipole force coupled to a single radial branch and a carrier transition

$$\begin{eqnarray}&&{H}_{{\ell }{\rm{I}}}=\displaystyle \sum _{i\lt j}{\tilde{J}}_{{ij}}^{x}{\sigma }_{i}^{x}{\sigma }_{j}^{x}-\displaystyle \sum _{i}\tilde{h}{\sigma }_{i}^{x}.\end{eqnarray} \tag{ 8 }$$

Instead of applying a strong transverse field to obtain the isotropic XY model [40, 41], let us consider a periodically modulated transverse field, which may arise from the cross-beam ac-Stark shift from a pair of co-propagating lasers with different frequencies. This is described by

$$\begin{eqnarray}&&{H}_{{\rm{m}}}(t)=\displaystyle \sum _{i}\displaystyle \frac{{{\rm{\Omega }}}_{{\rm{d}}}}{4}\mathrm{cos}({\omega }_{{\rm{d}}}t){\sigma }_{i}^{z},\end{eqnarray} \tag{ 9 }$$

where ${{\rm{\Omega }}}_{{\rm{d}}}$ is the strength of the transverse field, and ${\omega }_{{\rm{d}}}$ its modulation frequency. We note that the following results could as well be obtained for a transverse resonant carrier with an periodically modulated amplitude by simply exchanging ${\sigma }_{i}^{z}\to {\sigma }_{i}^{y}$ in the above equation.

We start by moving to an interaction picture with respect to the driving, to obtain the following dressed Hamiltonian

$$\begin{eqnarray}&&{H}_{{\ell }I}(t)=\displaystyle \sum _{i\lt j}{\tilde{J}}_{{ij}}^{x}{\sigma }_{i}^{+}{\sigma }_{j}^{-}+\displaystyle \sum _{i\lt j}{\tilde{J}}_{{ij}}^{x}{\mathfrak{f}}(t){\sigma }_{i}^{+}{\sigma }_{j}^{+}-\displaystyle \sum _{i}\tilde{h}\sqrt{{\mathfrak{f}}(t)}{\sigma }_{i}^{+}+{\rm{h.c.}},\end{eqnarray} \tag{ 10 }$$

where we have introduced the modulation function ${\mathfrak{f}}(t)={\rm{exp}}\{{\rm{i}}\frac{{{\rm{\Omega }}}_{{\rm{d}}}}{{\omega }_{{\rm{d}}}}\mathrm{sin}({\omega }_{{\rm{d}}}t)\}$, and the operators ${\sigma }_{i}^{\pm }=\frac{1}{2}({\sigma }_{i}^{x}\pm {\rm{i}}{\sigma }_{i}^{y})$. By using the Jacobi–Anger expansion of the exponential in terms of Bessel functions, this modulation function can be expressed as ${\mathfrak{f}}(t)={\sum }_{n\in {\mathbb{Z}}}{{\mathfrak{J}}}_{n}\left(\frac{{{\rm{\Omega }}}_{{\rm{d}}}}{{\omega }_{{\rm{d}}}}\right){{\rm{e}}}^{{\rm{i}}n{\omega }_{{\rm{d}}}t}$. We can now simplify the Hamiltonian considerably if we consider that the modulation frequency is much larger than the couplings of the Ising model (8), namely $| \tilde{h}| ,| {\tilde{J}}_{{ij}}^{x}| \ll {\omega }_{{\rm{d}}}$. By applying a rotating-wave approximation, we find a time-independent Hamiltonian

$$\begin{eqnarray}{H}_{{\ell }I}(t) & = & \displaystyle \sum _{i\lt j}{J}_{{ij}}^{x}{\sigma }_{i}^{+}{\sigma }_{j}^{-}+\displaystyle \sum _{i\lt j}{J}_{{ij}}^{x}{{\mathfrak{J}}}_{0}({{\rm{\Omega }}}_{{\rm{d}}}/{\omega }_{{\rm{d}}}){\sigma }_{i}^{+}{\sigma }_{j}^{+}\\ & & -\displaystyle \sum _{i}h{{\mathfrak{J}}}_{0}({{\rm{\Omega }}}_{{\rm{d}}}/2{\omega }_{{\rm{d}}}){\sigma }_{i}^{+}+{\rm{h.c.}},\end{eqnarray} \tag{ 11 }$$

where one observes that some of the coupling strengths are dressed by the zero Bessel function. Higher-order resonances described by higher Bessel functions can be neglected regardless of the value of the ratio ${{\rm{\Omega }}}_{{\rm{d}}}/{\omega }_{{\rm{d}}}$. This is justified by a rotating-wave approximation since $\mathrm{max}({J}_{{ij}}){{\mathfrak{J}}}_{n}({{\rm{\Omega }}}_{{\rm{d}}}/{\omega }_{{\rm{d}}})\ll {\omega }_{{\rm{d}}}$ is always fulfilled as all Bessel functions are bounded by ${{\mathfrak{J}}}_{n}({{\rm{\Omega }}}_{{\rm{d}}}/{\omega }_{{\rm{d}}})\lt 1$. By moving back to the standard Pauli spin operators, we obtain the desired ℓXY model (1), ${H}_{{\ell }I}(t)={H}_{{\ell }\mathrm{XY}}$, with the following parameters

$$\begin{eqnarray}{J}_{{ij}}^{x} & = & {\tilde{J}}_{{ij}}^{x}(1+{{\mathfrak{J}}}_{0}({{\rm{\Omega }}}_{{\rm{d}}}/{\omega }_{{\rm{d}}}))/2,\\ {J}_{{ij}}^{y} & = & {\tilde{J}}_{{ij}}^{x}(1-{{\mathfrak{J}}}_{0}({{\rm{\Omega }}}_{{\rm{d}}}/{\omega }_{{\rm{d}}}))/2,\\ {h}_{\phantom{{ij}}} & = & \tilde{h}{{\mathfrak{J}}}_{0}({{\rm{\Omega }}}_{{\rm{d}}}/2{\omega }_{{\rm{d}}}).\end{eqnarray} \tag{ 12 }$$

Hence, by controlling two ratios $\tilde{h}/{\tilde{J}}_{0}^{x}$, and ${{\rm{\Omega }}}_{{\rm{d}}}/{\omega }_{{\rm{d}}}$, we can access the full phase diagram of the target ℓXY model (1). We note that this scheme might be considered as a spin version of the so-called coherent destruction of tunneling for electrons in solids under periodic electric fields [43], and is the simplest possible modulation scheme that can lead to interesting effective Hamiltonians. In the context of trapped ions, other driving terms have been exploited to simulate the effects of synthetic gauge fields in the vibrational or spin sectors [44, 45].

Before moving to the next section, where we exploit the tool of quantum dualities for quantum simulations, let us summarize the ingredients that we have introduced so far. (i) By loading the ion crystal in a controlled fashion, we can design the number of spins N in the synthetic quantum magnets as desired. (ii) By combining the resonance fluorescence in a cycling transition [24] with global single-spin rotations in the Bloch sphere (i.e. single-qubit gates), we can measure the observables $\langle {\sigma }_{i}^{\alpha }\rangle$, $\langle {\sigma }_{i}^{\alpha }{\sigma }_{j}^{\alpha }\rangle$, $\langle {\sigma }_{i}^{\alpha }{\sigma }_{j}^{\alpha }{\sigma }_{k}^{\alpha }\rangle ,\langle {\sigma }_{i}^{\alpha }{\sigma }_{j}^{\alpha }{\sigma }_{k}^{\alpha }{\sigma }_{l}^{\alpha }\rangle$, and so on. (iii) By using carrier transitions and far-detuned spin-dependent dipole forces, either along two different vibrational axes with different trap frequencies, or combining a single force with a periodic modulation, we can obtain a synthetic longitudinal XY model with dipolar couplings (1). These three ingredients will be fundamental to propose a dual quantum simulator in the following section. We shall argue that, even if the dipolar XY model in a longitudinal field does not look more exotic than the standard quantum Ising model, it can lead to very interesting phenomena such as quantum frustration when complemented by quantum dualities and certain local measurements which, although complicated for other setups, are accessible in trapped-ion experiments.

The notion of duality in physics, which first appeared in connection to the equations of electromagnetism in the absence of sources, has become a far reaching concept in different disciplines. In this work, we shall focus on the use of dualities to understand the properties of many-body lattice models, which started with a seminal work on the self-duality of the Ising model on the square lattice [46]. This property permitted locating the critical temperature of the model prior to its exact solution [4], and turned out to be a powerful concept that can be generalized to other situations [47], including also the quantum-mechanical regime [21, 22].

3.1. Quantum duality transformation

In essence, a duality transformation relates the properties of a particular model in the original lattice Λ with those of a transformed model in the dual lattice${{\rm{\Lambda }}}^{*}$. In 1D, which is the regime of interest to our work, the dual lattice is obtained by placing vertices at the links of the original lattice, and setting bonds between those vertices separated by a site of the original lattice. Therefore, the dual lattice of a 1D chain is simply another chain that has been translated by half a lattice constant. Typically, this transformation is defined for infinite Bravais lattices, and aims at giving a different perspective of the model under study in the so-called thermodynamic limit. However, since we are interested in small-scale synthetic magnets, one needs to consider the effects of boundary conditions, which map an original N-site chain ${{\rm{\Lambda }}}_{N}$ onto an $(N+1)$-site dual chain ${{\rm{\Lambda }}}_{N+1}^{*}$

Once these lattices have been defined, let us introduce the quantum duality on the spin operators [21, 22]. The ${\mathfrak{su}}(2)$ algebra of the spin operators is preserved by defining the dual spin operators as follows

$$\begin{eqnarray}&&{\sigma }_{i}^{x}={\tau }_{i-1}^{z}{\tau }_{i}^{z},\phantom{\rule{2ex}{0ex}}{\sigma }_{i}^{y}=\displaystyle \prod _{j\lt i}{\tau }_{j}^{x},\phantom{\rule{2ex}{0ex}}\forall i\in {{\rm{\Delta }}}_{N},\end{eqnarray} \tag{ 14 }$$

where we define the index $i\in \{1,2,\cdots ,N\}$ for the original lattice ${{\rm{\Delta }}}_{N}$, and $i\in \{0,1,\cdots ,N\}$ for the dual lattice ${{\rm{\Delta }}}_{N+1}^{*}$.

Then, the dual Hamiltonian to the ℓXY model (1) becomes

$$\begin{eqnarray}&&{H}_{{\ell }\mathrm{XY}}^{{\rm{dual}}}=\displaystyle \sum _{i\gt j}\left({J}_{{ij}}^{x}{\tau }_{i-1}^{z}{\tau }_{i}^{z}{\tau }_{j-1}^{z}{\tau }_{j}^{z}+{J}_{{ij}}^{y}\displaystyle \prod _{i\leqslant k\lt j}{\tau }_{k}^{x}\right)-\displaystyle \sum _{i}h{\tau }_{i-1}^{z}{\tau }_{i}^{z},\end{eqnarray} \tag{ 15 }$$

where the sums must be extended to the dual lattice ${{\rm{\Lambda }}}_{N+1}^{*}$, and thus to $N+1$ sites. At first sight, this dual mapping does not seem to produce any interesting result, since the dual Hamiltonian seems to be more convoluted than the original one. However, exploiting the fast dipolar decay and some additional properties of the spin–spin couplings (7), this dual Hamiltonian can host a variety of exotic effects. Let us postpone this discussion for the following sections, and address first a question of relevance for the dual quantum simulator.

3.2. Quantum dual measurements

Usually, quantum dualities are used as theoretical tools that allow to understand certain aspects of a particular lattice model from a different perspective. In this manuscript, we are instead proposing to use them experimentally, which is usually hampered by the non-local character of the dual operators (14). In order to understand the properties of the dual model (15), one typically studies two-point correlators in the dual basis, which become highly nonlocal correlators in the original lattice, such as

$$\begin{eqnarray}&&\langle {\tau }_{i}^{z}{\tau }_{i+{\ell }}^{z}\rangle =\langle {\sigma }_{i+1}^{x}{\sigma }_{i+2}^{x}\cdots {\sigma }_{i+{\ell }}^{x}\rangle .\end{eqnarray} \tag{ 16 }$$

Therefore, in order to exploit the quantum duality experimentally and understand properties of the model (15) by performing experiments with the physical Hamiltonian (1), one needs to measure string-order-like parameters, which is usually impossible in most physical setups. However, as argued in the previous sections, these type of observables are exactly the ones that can be obtained via the combination of single-qubit gates and fluorescence in trapped-ion experiments.

Apart from correlation functions, also spectral properties give interesting insight into the behavior of a physical system, and important properties such as energy gaps of low-lying excitations are the same for the original model and its dual. Accordingly, spectroscopic measurements in the spirit of the recent experiments [41, 48] may provide an alternative way of obtaining relevant information valid for both models.

Before entering into the discussion about the exotic magnetic phases that the Hamiltonian (15) can host, let us also comment on the other highly unusual property of our synthetic quantum magnets: the possibility of exactly controlling the number of spins N. Critical phenomena and quantum phase transitions take place in the thermodynamic limit ($N\to \infty$). Although this is a mathematical idealization since real systems are always finite, this type of predictions agree considerably well with those based on moderately large samples, as predicted by finite size scaling (FSS) [49]. Although, strictly speaking, phase transitions can only occur at the thermodynamic limit, FSS can be considered as a window to extract their infinite-size characteristics (e.g. critical points and exponents) by studying the scaling of certain observables with the system size. As occurs with quantum dualities, FSS has been mainly a theoretical tool used in combination with numerical simulations of small systems of increasing size. On the other hand, experimental FSS in real materials would be hampered by difficulties on (i) controlling accurately N, and (ii) distinguishing finite-size effects from other spurious rounding effects (e.g. disorder, impurities, etc). This situation has recently changed with trapped-ion experiments [28], where the number of Ising spins can be controlled exactly, and where typical disorder and impurity effects are totally absent. Moreover, the possible rounding effects caused by other sources of noise can be experimentally controlled and identified.

In the following two sections, we will combine the duality transformation, FSS, and non-local observables, to show that the mild-looking Hamiltonian (1) can indeed simulate a variety of exotic magnetic phenomena.

In this section, we want to show that the dual quantum simulator can be used to explore the interplay of frustration and quantum fluctuations. Let us first start with a plausibility argument. One can rearrange the dual Hamiltonian (15) as

$$\begin{eqnarray}&&{H}_{{\ell }\mathrm{XY}}^{{\rm{dual}}}={H}_{{\rm{qANNNI}}}(-h,{J}_{i,i+1}^{x},{J}_{i,i+1}^{y})+{\rm{\Delta }}H,\end{eqnarray} \tag{ 17 }$$

where ${H}_{{\rm{qANNNI}}}(-h,{J}_{i,i+1}^{x},{J}_{i,i+1}^{y})$ is the so-called quantum axial next-nearest-neighbor Ising Hamiltonian (qANNNI), to be defined below. If the ${\ell }$ XY-model (1) was restricted to nearest-neighbor interactions, i.e. if ${J}_{{ij}}^{\alpha }\propto {\delta }_{\langle i,j\rangle }$, the dual mapping between ℓXY and qANNNI model would be perfect, that is, the remainder ${\rm{\Delta }}H=0$ would vanish. However, since our starting point is the ℓXY model with dipolar interactions, ${\rm{\Delta }}H$ will be non-zero introducing a perturbation to the dual mapping.

The Hamiltonian of the qANNNI model is the one of a transverse Ising model with frustrated nearest-neighbor and next-nearest-neighbor interactions

$$\begin{eqnarray}&&{H}_{{\rm{qANNNI}}}({J}_{1},{J}_{2},B)=\displaystyle \sum _{i}({J}_{1}{\tau }_{i}^{z}{\tau }_{i+1}^{z}+{J}_{2}{\tau }_{i}^{z}{\tau }_{i+2}^{z}+B{\tau }_{i}^{x}).\end{eqnarray} \tag{ 18 }$$

Here, ${J}_{1}\lt 0$ is a ferromagnetic (FM) nearest-neighbor coupling that corresponds to the longitudinal field of the original Hamiltonian (1). This FM interaction competes against an antiferromagnetic ${J}_{2}\gt 0$ next-nearest-neighbor coupling, corresponding to the nearest-neighbor XX couplings of the original model, and a transverse magnetic field B, corresponding to the nearest-neighbor YY couplings of the original model. Note that these competing Ising interactions can be described in a two-leg ladder with triangular motifs, which clarifies the origin of the frustration (see figure 1). The parameter equivalence under the duality is thus

$$\begin{eqnarray}&&{J}_{1}=-h,\phantom{\rule{2ex}{0ex}}{J}_{2}={J}_{i,i+1}^{x},\phantom{\rule{2ex}{0ex}}B={J}_{i,i+1}^{y}.\end{eqnarray} \tag{ 19 }$$

This shows that for exploring the rich physics of the qANNNI model via the ℓXY model, the XY interactions need to be chosen antiferromagnetic. Let us also highlight the importance of the longitudinal character of the magnetic field: if it was transversal instead of longitudinal, the system would always lie in a gapless phase with power-law correlations, but there would not be any quantum phase transition as a function of the anisotropy of the spin couplings, nor any frustration effect as a function of the ratio of the transverse field and the spin couplings.

Let us emphasize that the frustration range of the qANNNI model, given by the ratio of next-nearest- to nearest-neighbor couplings ${J}_{2}/| {J}_{1}|$, corresponds to the ratio of two different couplings ${J}_{i,i+1}^{x}/h$ in the original model (1) that arise from totally different sources, i.e. a spin-dependent force and a carrier transition. Accordingly, it is simpler to reach all regimes of physical interest ${J}_{2}/| {J}_{1}| \lessgtr 1/2$ by tuning this ratio in the physical model (1), than it would be to reach them by shaping the long-range tail of a bare quantum Ising model [32]. In fact, as ${J}_{2}/| {J}_{1}| \to 1$, it would be no longer justified to neglect the remaining longer-range tail of the bare Ising model, as these additional terms are likely to modify severely the phase diagram. Our method of controlling the range of frustration also seems more straightforward than modifying the crystalline structure in Penning [29] and surface [30] traps, or changing the direction of the lasers/tilting the crystal [31] in common rf-traps.

In addition to the qANNNI Hamiltonian, the long-range nature of the interactions in (1) leads to the following perturbation

$$\begin{eqnarray}&&{\rm{\Delta }}H=\displaystyle \sum _{i=1}^{N+1}\displaystyle \sum _{j=i+2}^{N+1}({J}_{{ij}}^{x}{\tau }_{i-1}^{z}{\tau }_{i}^{z}{\tau }_{j-1}^{z}{\tau }_{j}^{z}+{J}_{{ij}}^{y}\displaystyle \prod _{i\leqslant k\lt j}{\tau }_{k}^{x}),\end{eqnarray} \tag{ 20 }$$

which contains the dipolar tail of the phonon-mediated interactions starting form the next-nearest-neighbor couplings. Due to the fast dipolar decay (7), the next-nearest-neighbor couplings are almost one order of magnitude smaller than the nearest-neighbor terms in equation (18), and the longer-range terms get reduced even further. Hence, one can argue that this perturbation will not modify in any essential manner the phase diagram of the qANNNI model (18). Although the duality between the nearest-neighbor models is already known to bear accurate results, we will show below by numerical calculation that our plausibility argument is correct, and that the additional long-range contributions do not modify the usefulness of the duality mapping for quantum simulation purposes.

The model in equation (18) is the quantum-mechanical version of the classical ANNNI model [50, 51] in a square lattice, as can be proved by applying the quantum-classical mapping [5] in the present case [52]. The classical 2D model, which describes stacked Ising chains with competing FM nearest-neighbor and anti-ferromagnetic next-nearest-neighbor couplings at finite temperatures, is considered to be a paradigm in the physics of magnetic frustration and commensurate/incommensurate phases (i.e. spatially modulated arrangements of the magnetic dipoles with a period that is commensurate/incommensurate with the lattice) [53]. In addition to the typical second-order phase transitions describing order-disorder phenomena in Ising magnets, this model displays different lines separating the commensurate/incommensurate phases, such as Kosterlitz–Thouless [54] and Pokrovsky–Talapov [55] phase transitions, or a disorder line [56] connecting unmodulated/modulated disordered paramagnets. All these thermal phenomena find an analogue in the ground state of the quantum-mechanical model (18), where the transverse field B plays the role of the temperature by introducing quantum fluctuations that drive the different phase transitions.

In the following, we make an exhaustive numerical study to assess the importance of the dipolar terms in the trapped-ion realization, and the possibility of observing such a rich phase diagram with state-of-the-art experimental conditions.

4.1. Large ground state degeneracy

A hallmark of frustration, sometimes even regarded as its defining property, is the existence of a vastly degenerate ground state manifold that a arises from the impossibility of minimizing simultaneously the conflicting interactions [13]. In the dual model (18), this frustration arises from the competition between FM nearest-neighbor and anti-ferromagnetic next-nearest-neighbor interactions. Triads of sites $(i,i+1,i+2)$ define a triangular motif, where the Ising interactions for ${J}_{2}/| {J}_{1}| =1/2$ at B = 0 cannot be simultaneously minimized, and thus become frustrated. In fact, the number ${D}_{{\rm{qANNNI}}}(N)$ of degenerate ground states at this frustration point [57] grows exponentially with system size N

$$\begin{eqnarray}&&{D}_{{\rm{qANNNI}}}(N)=\displaystyle \frac{2}{\sqrt{5}}\left[{\left(\displaystyle \frac{1+\sqrt{5}}{2}\right)}^{N}+{\left(\displaystyle \frac{1-\sqrt{5}}{2}\right)}^{N}\right].\end{eqnarray} \tag{ 21 }$$

According to the duality mapping, the nearest-neighbor limit of the XY model in a longitudinal field (1) should show the same exponential growth in the ground state manifold for h = 0, and ${J}_{i,i+1}^{x}=2{J}_{i,i+1}^{y}$. Note, however, that the duality transformation (14) removes the ${{ \mathcal Z }}_{2}$-symmetry of the Ising model, and thus halves the number of degenerate states in the original model

$$\begin{eqnarray}&&{D}_{{\ell }{\rm{XY}}}(N)=\displaystyle \frac{{D}_{{\rm{qANNNI}}}(N)}{2}.\end{eqnarray} \tag{ 22 }$$

As discussed above, for open boundary conditions, one also needs to take into account the fact that the duality maps a system of N spins onto a system with $N+1$ bond operators. We also note that it is possible to preserve the ${{ \mathcal Z }}_{2}$ symmetry by modifying the duality transformation such that the transverse field is not applied to all spins [58], but here we stick to the standard duality transformation (14).

We have verified the counting of equation (22) for small systems up to N = 14, where the XY interaction is truncated to nearest neighbors. Turning our attention to the dipolar ℓXY model (1), the addition of the long-range tail is especially disturbing around this maximally frustrated regime, as the vast number of degenerate ground states turns any perturbation, no matter how small, into a highly non-perturbative problem. Nevertheless, the dipolar system still exhibits some traces of the exponentially large degeneracies in the 'clean' model. As demonstrated in figure 2 by contrasting the 350 lowest eigen-energies of the dipolar model to the energies of the nearest-neighbor model, the dipolar system exhibits a low-energy manifold separated from higher states by a spectral gap, and the dimension of this manifold is precisely given by equation (22).

Zoom In Zoom Out Reset image size

4.2. Phase diagram for finite chains

We now explore numerically the phase diagram of the dipolar XY model in a longitudinal field (1), assessing how far it resembles the qANNNI model (18). Let us thus review the features of the qANNNI phase diagram, which are in one-to-one correspondence with the 2D classical ANNNI model [53].

Setting B = 0, the qANNNI Hamiltonian becomes classical, and the phase diagram is derived easily: For ${J}_{2}/| {J}_{1}| \lt 0.5$, the system is in a FM phase, with a two-fold degenerate ground state having all spins polarized along z. For ${J}_{2}/| {J}_{1}| \gt 0.5$, the system is the the anti-phase (AP) with a four-spin unit cell $\uparrow \uparrow \downarrow \downarrow$. For commensurability purposes, one should take a system with a number of spins N divisible by 4. For open boundaries, one obtains a two-fold degenerate ground state (${{ \mathcal Z }}_{2}$ spin-inversion symmetry), while in the case of periodic boundaries, translational symmetry yields a four-fold degenerate ground state (${{ \mathcal Z }}_{2}\times {{ \mathcal Z }}_{2}$ symmetry by the Cartesian product of the spin-inversion symmetries at even and odd lattice sites). The critical point between the FM phase and the AP corresponds to the frustration point ${J}_{2}/| {J}_{1}| =0.5$ addressed in the previous section, where the model yields an exponentially large ground state manifold given by (21). If a strong magnetic field $B\gg | {J}_{1}| ,{J}_{2}$ is present, the system will exhibit a paramagnetic (PM) phase, with two-point spin correlations that decay exponentially fast with the distance.

Several studies, including exact diagonalization of an effective domain-wall description [59], finite-size scaling (FSS) [60], or recent matrix-product state (MPS) calculations [61] predict the direct vicinity of the PM and FM phase, with a second-order quantum phase transition along a critical line that bounds the entire FM phase. The FM–PM transition belongs to the same universality class as the standard quantum Ising model [7]. As shown by the density-matrix renormalization group (DMRG) study of [62], a so-called disorder line, coinciding with the Peschel–Emery line [56], divides the PM phase into two regimes: in direct vicinity to the FM phase, the PM phase is unmodulated, while for larger values of B the exponential decay of correlations is accompanied by a modulation of the correlation function.

For ${J}_{2}/| {J}_{1}| \gt 0.5$, a so-called floating phase (FP) separates the AP and the PM phase, as evidenced by the quantum Monte Carlo study in [63], by the DMRG studies in [61, 64], or by perturbation theory calculations in [65]. This intermediate phase is characterized by modulated, algebraically decaying spin–spin correlations [59]:

$$\begin{eqnarray}&&\langle {\tau }_{i}^{z}{\tau }_{i+d}^{z}\rangle \propto {d}^{-\rho }\mathrm{cos}(\pi {q}{d}),\end{eqnarray} \tag{ 23 }$$

with parameters $q\in \left[0,\frac{1}{2}\right]$, and $\rho ={(1-q)}^{2}/2$. The MPS data [61] suggest that the AP–FP commensurate-incommensurate Pokrovsky–Talapov transition is second-order, while the FP–PM transition is believed to be of the Kosterlitz–Thouless type [61, 64]. We note that the determination of the phase diagram in this regime is difficult, as important quantities like the energy gap strongly depend on the system size.

Once the properties of the qANNNI model have been discussed, we can start addressing the effects of the long-range tail through the numerical study of the ℓXY model (1).

4.2.1. Parameter region ${J}_{2}/| {J}_{1}| \lt 0.5$

In the regime of low frustration, ${J}_{2}/| {J}_{1}| \lt 0.5$, the dual qANNNI model behaves similarly to the standard quantum Ising model, with a FM–PM second-order transition. Boundary and/or finite-size effects play a quantitative, but not a qualitative role. The transition between FM–PM has a relatively sharp signature in the spin–spin correlation function at sufficiently large distance. As the PM phase is characterized by exponentially fast correlations, a drop of the correlations marks the boundary. In the original model, a correlation $\langle {\tau }_{i}^{z}{\tau }_{i+{\ell }}^{z}\rangle$ translates into a non-local ℓ-point correlation function $\langle {\sigma }_{i+1}^{x}{\sigma }_{i+2}^{x}...{\sigma }_{i+{\ell }}^{x}\rangle$, which as discussed around equation (16) can be measured in trapped-ion experiments. Since measuring string-order-like parameters is more sensitive to errors than measuring local order parameters, it is important to notice that the main features of the phase diagram are displayed already by short-range two- and four-spin operators, with ${\ell }=2$ and ${\ell }=4$. The results are shown in figures 3 and 4. In these figures, we compare the results for (a) the nearest-neighbor limit of the ℓXY model, (b) its full dipolar version (1), and (c) the corresponding correlations $\langle {\tau }_{i}^{z}{\tau }_{i+{\ell }}^{z}\rangle$ of the associated dual model (18). In all cases, we have applied open boundary conditions, and averaged the spin–spin correlations over all lattice sites. One can see a very nice agreement of these numerical results between the ℓXY model and its qANNNI dual. Note that, in the case of open boundaries, the qANNNI model of N spins corresponds to the dual of a ℓXY model of $N-1$ spins, and this is the reason why the spin numbers differ.

Zoom In Zoom Out Reset image size

As expected, the nearest-neighbor ℓXY model and the qANNNI model behave identically. A comparison of them with the dipolar ℓ XY model shows some small differences. For instance, the FM phase is less extended in the presence of dipolar interactions. This is due to the fact that in equation (1) the dual FM order is established by the magnetic field term (19), while PM order is due to interactions. Therefore, the dipolar tail, enhancing the interaction, acts in favor of the PM phase and shifts the FM–PM transition towards smaller values of $B/| {J}_{1}|$. A similar reasoning explains why, along B = 0, the FM phase vanishes for ${J}_{2}/| {J}_{1}| \lt 0.5$ in the dipolar model. We also notice that the critical 'point' is broadened by dipolar interactions, with a critical region between the FM–AP transition at B = 0.

Although these differences become more pronounced if the range of interactions is further increased, we have numerically checked that the main qualitative features of the phase diagram remain unchanged even for a power-law decay with coefficients $k\lesssim 2$. While these longer-range scenarios are simpler to realize in an experiment, the best quantitative agreement with the nearest-neighbor model is obtained in the dipolar case.

As a possible approach to determine the FM–PM transition line, we use FSS of the mass gap. Therefore, we define the scaled energy gap

$$\begin{eqnarray}&&{{\rm{\Delta }}}_{N}(B)={N}^{z}[{E}_{1}(B)-{E}_{0}(B)],\end{eqnarray} \tag{ 24 }$$

with z the dynamical critical exponent, in the following taken to be 1. The energies E₁ and E₀ correspond to the first excited state, and to the ground state of the original ℓXY model (1), respectively. At criticality, ${{\rm{\Delta }}}_{N}(B)$ should be independent from the size of the system, and thus all the curves ${{\rm{\Delta }}}_{N}(B)$ for different values N must cross at one common point. This allows us to extract the critical field strength ${B}_{{\rm{c}}}$ for a given value of J₂. The data obtained in this way, taking into account system sizes up to N = 15, is given by the dots in figures 3 and 4. We highlight how the drop of the four-point correlator in figure 4 agrees extremely well with the phase boundary obtained via scaling behavior of the mass gap. Let us note that the required energy gap energies can be measured experimentally using the spectroscopic trapped-ion methods put forth in [41, 48]. Combined with the unique property of controlling exactly the number of spins, would allow the trapped-ion setups to perform the first FSS in a real experiment.

Zoom In Zoom Out Reset image size

As an alternative to the energy gap, other observables, such as magnetization and correlations, are equally well suited for performing a FSS, and might be easier to measure in a trapped-ion experiment. Assuming the $\beta =1/8$ exponent of the quantum Ising model, one could scale local magnetization of the ground state as $\langle {\tau }_{i}^{z}\rangle {N}^{1/8}$, which should become independent from N at the phase boundary. In the case of the ℓXY model, we would need to examine the dual correlator to $\langle {\tau }_{i}^{z}\rangle$, that is, $\langle {\prod }_{j\leqslant i}{\sigma }_{j}^{x}\rangle$. As an example, we have chosen a fixed value ${J}_{2}=-0.1{J}_{1}$ in figure 5, and varying the field strength B, we determine its critical value ${B}_{{\rm{c}}}$ by the cut of the curves correspoding to different system sizes. The obtained value, ${B}_{{\rm{c}}}=0.566(10)$, agrees with the corresponding value obtained via FSS of the gap, ${B}_{{\rm{c}}}=0.574(5)$.

Zoom In Zoom Out Reset image size

FSS also allows to determine critical exponents by assuming a certain scaling relation [66], namely

$$\begin{eqnarray}&&{{\rm{\Delta }}}_{N}(B)\sim f({N}^{1/\nu }(B-{B}_{{\rm{c}}})),\end{eqnarray} \tag{ 25 }$$

with ν the critical exponent of the correlation length, ${B}_{{\rm{c}}}$ the critical field strength of the FM–PM transition already calculated, and f(x) a universal scaling function. From equation (25), it follows that

$$\begin{eqnarray}&&\nu =\displaystyle \frac{\mathrm{log}(N/{N}^{\prime })}{\mathrm{log}(\partial {{\rm{\Delta }}}_{N}/\partial {{\rm{\Delta }}}_{{N}^{\prime }})},\end{eqnarray} \tag{ 26 }$$

where $\partial {{\rm{\Delta }}}_{N}\equiv (\partial {{\rm{\Delta }}}_{N}(B)/\partial B){| }_{B={B}_{{\rm{c}}}}$. Using equation (26), we have determined ν from the data ${{\rm{\Delta }}}_{N}$ with N up to 15, using the ${B}_{{\rm{c}}}$ obtained before. The results are shown in table 1, for different values of J₂ and evaluated using N = 15 and ${N}^{\prime }=14$, with errors assuming an uncertainty of $\delta {B}_{{\rm{c}}}=0.005$. For all models (qANNNI, nearest-neighbor ℓXY, and dipolar ℓXY), we obtain a critical exponent ν in the range between 0.9 and 1.1, in accordance with the expected Ising universality class $\nu =1$. Error estimates suggest that the most accurate results are obtained, as could be expected, far off the frustration point ${J}_{2}/| {J}_{1}| =0.5$, with $\delta \nu =0.02$. With this, the expected Ising exponent, $\nu =1$, is located within an interval of up to five times the standard error. We expect that a systematic underestimation of the critical field strength due to the finite size of our samples is responsible for this discrepancy. The best agreement with the Ising value is obtained in the nearest-neighbor ℓXY, with values spreading between 0.94 and 1.01. Remarkably, the dipolar version of the ℓXY model produces results which are slightly better than those obtained for the original qANNNI model, see table 1.

Table 1.  Critical field strength ${B}_{{\rm{c}}}$ and critical exponent ν for the FM–PM transition.

${J}_{2}/| {J}_{1}|$	${B}_{{\rm{c}}}/| {J}_{1}|$	ν	${B}_{{\rm{c}}}/| {J}_{1}|$	ν	${B}_{{\rm{c}}}/| {J}_{1}|$	ν
	(n.n. ℓXYmodel)	(n.n. ℓXYmodel)	(dipolar ℓXYmodel)	(dipolar ℓXYmodel)	(qANNNI model)	(qANNNI model)
1/50	0.973(5)	0.94(2)	0.695(5)	0.90(2)	0.959(5)	1.09(2)
6/50	0.790(5)	0.95(2)	0.541(5)	0.91(2)	0.780(5)	1.09(3)
11/50	0.595(5)	0.96(2)	0.374(5)	0.92(3)	0.592(5)	1.07(4)
16/50	0.388(5)	1.01(6)	0.184(5)	0.94(5)	0.380(5)	1.13(17)

4.2.2. Parameter region ${J}_{2}/| {J}_{1}| \gt 0.5$

For various reasons, the regime ${J}_{2}/| {J}_{1}| \gt 0.5$ is more difficult to capture accurately by studying a small-sized system. First of all, one must be very careful with the number of spins studied, and the choice of the boundary. Since the AP has a four-spin unit cell, one would take system sizes divisible by 4, such that the classical ANNNI model (B = 0) shows the expected FM–AP transition for both open and periodic boundary conditions at ${J}_{2}/| {J}_{1}| =0.5$. However, when we turn to the ℓXY model, the situation is different: if we again choose N divisible by 4, only the system with periodic boundary conditions exhibits a direct FM–AP transition. In contrast, the system with open boundaries, which is the experimentally relevant case for the small-scale trapped-ion magnets, shows an intermediate phase, extending from $0.5\lt {J}_{2}/| {J}_{1}| \lt 1$.

The occurrence of this intermediate phase can be understood from simple energy considerations in the classical system, i.e. in the ℓXY model without YY interactions. The FM case is characterized by a single, fully polarized ground state, whereas the antiphase has Néel order. We assume an intermediate state with FM order for ${N}_{{\rm{f}}}$ subsequent spins and Néel order for ${N}_{{\rm{a}}}=N-{N}_{{\rm{f}}}$ spins. The energy of this configuration is given by

$$\begin{eqnarray}&&\displaystyle \frac{E}{| {J}_{1}| }={N}_{{\rm{a}}}\left(1-2\displaystyle \frac{{J}_{2}}{| {J}_{1}| }\right)+N\left(\displaystyle \frac{{J}_{2}}{| {J}_{1}| }-1\right)-\displaystyle \frac{{J}_{2}}{| {J}_{1}| },\end{eqnarray} \tag{ 27 }$$

where we have assumed ${N}_{{\rm{a}}}\lt N$. For ${J}_{2}/| {J}_{1}| \lt 0.5$, the ${N}_{{\rm{a}}}$ term contributes positively to the energy, and thus the ground state configuration must have ${N}_{{\rm{a}}}=0$, that is, the system is in the FM phase. For ${J}_{2}/| {J}_{1}| \gt 0.5$, ${N}_{{\rm{a}}}$ should attain its maximal value, which in the formula above is $N-2$. The energy for ${N}_{{\rm{a}}}=N$ is simply given by $E/| {J}_{1}| =-({J}_{2}/| {J}_{1}| )(N-1)$. Comparison of the two values shows that the antiphase (i.e. ${N}_{{\rm{a}}}=N$) becomes favorable only for ${J}_{2}/| {J}_{1}| \gt 1$, while for $0.5\lt {J}_{2}/| {J}_{1}| \lt 1$, the system has two domains, a FM one and a domain in the antiphase. Independent from the size of the system, the FM domain for $0.5\lt {J}_{2}/| {J}_{1}| \lt 1$ is of size ${N}_{{\rm{f}}}=2$, thus for large systems the intermediate phase becomes indistinguishable from the antiphase.

As we announced before, for a system with periodic boundary conditions, the classical energy is always given by

$$\begin{eqnarray}&&\displaystyle \frac{E}{| {J}_{1}| }={N}_{{\rm{a}}}\left(1-2\displaystyle \frac{{J}_{2}}{| {J}_{1}| }\right)+N\left(\displaystyle \frac{{J}_{2}}{| {J}_{1}| }-1\right),\end{eqnarray} \tag{ 28 }$$

for all possible values of ${N}_{{\rm{a}}}$. Therefore, the transition from a fully FM system to a fully AP system occurs without any intermediate phase.

To solve this disagreement between qANNNI model and ℓXY model, we have to consider the fact that the dual operators are bond operators that reside on the links of the lattice (13). Therefore, the open qANNNI chain of $N=4m$ spins ($m\in {Z}^{+}$) would be the dual model of a Hamiltonian with $4m-1$ spin operators. Accordingly, we should find a much better agreement between the diagram for N = 15 original spins, and N = 16 spins in the dual qANNNI model. This expectation is clearly confirmed by our numerical results (see figures 3, 4), which show that the odd number ℓXY model does not present an intermediate phase, but simply the expected FM–AP transition from the dual qANNNI model.

In the quantum case, $B\ne 0$, the system is expected to undergo two quantum phase transitions: the AP–FP and the FP–PM transitions. According to an MPS study of the qANNNI model [61], the AP–FP transition is of second order, while the FP–PM is of higher order. Determining the phase boundaries in the thermodynamic limit is difficult, as due to the modulated nature of the FP, the minima of the mass gap strongly depend on the system size N. In principle, as was done in [62] in the framework of a DMRG study for hundreds of spins, it is still possible to perform FSS, if one interpolates between different minima of the mass gap ${{\rm{\Delta }}}_{N}(B)$.

Without this costly procedure for extracting the thermodynamic limit, the AP–FP transition at a fixed finite system size can easily be detected by looking at the spin–spin correlators: sufficiently close to the frustration point, a sudden drop of the four-point correlations clearly marks a phase boundary in the qANNNI model, the nearest-neighbor ℓXY model, and the dipolar ℓXY model (see figure 4). To demonstrate that this drop indeed corresponds to the AP–FP transition, we first note that, in the language of the ℓXY model, the antiphase correlations are characterized by a Néel order of the original spins. Accordingly, the AP spin–spin correlation function is given by ${c}_{{\rm{AP}}}{(d):= \langle {\sigma }_{1}^{x}{\sigma }_{1+d}^{x}\rangle =(-1)}^{d}$. We thus introduce the overlap of correlations as

$$\begin{eqnarray}&&o{({J}_{2},B)=\displaystyle \sum _{d=1}^{N-1}(-1)}^{d}\langle {\rm{GS}}({J}_{2},B)| {\sigma }_{1}^{x}{\sigma }_{1+d}^{x}| {\rm{GS}}({J}_{2},B)\rangle .\end{eqnarray} \tag{ 29 }$$

For both the nearest-neighbor and the dipolar model with N = 15, the overlap is plotted in figure 6 as a function of B for selected values of J₂. The drop in overlap corresponds to the vanishing of AP order, and completely agrees with the drop of correlations in figures 3 and 4. However, for larger values of ${J}_{2}/| {J}_{1}| \gtrsim 1$, the function $o({J}_{2},B)$ becomes smooth over the full range of B, rendering it impossible to extract critical values of B. The presence of dipolar interactions shifts the AP–FP transition to smaller values of $B/| {J}_{1}|$, in comparison to the nearest-neighbor ℓXY model.

Zoom In Zoom Out Reset image size

While identifying the AP, and determining its boundary, is possible even for small systems due to the very characteristic correlations of the AP, our method does not provide information about the universality class of the transition. As done in [61, 64], this information can be obtained from the scaling of the entanglement entropy in sufficiently large systems. Such procedure also allows to determine the phase diagram beyond the AP, that is, the position of the higher-order phase transition between FP and PM phase.

Although trapped ions yet do not reach the required system size for identifying the critical behavior at the FP–PM transition, let us nevertheless provide some numerical evidence by studying the scaling of the entanglement entropy in the ℓXY model. Therefore, we first define the entanglement entropy through the nth bond of a system with N spins as

$$\begin{eqnarray}&&S(N,n)=-{{\rm{Tr}}}_{[1,...,n]}({\rho }_{[1,...,n]}\mathrm{ln}{\rho }_{[1,...,n]}),\end{eqnarray} \tag{ 30 }$$

where ${\rho }_{[1,...,n]}\equiv {{\rm{Tr}}}_{[n+1,...,N]}| {\rm{\Psi }}\rangle \langle {\rm{\Psi }}|$ the density matrix of the left part of the system (containing spins 1 to n). The system is assumed to be in a pure state $| {\rm{\Psi }}\rangle$. Quantum criticality is reflected by a scaling of the entanglement entropy as

$$\begin{eqnarray}&&S(N)\simeq \displaystyle \frac{c}{6}\;{\mathrm{log}}_{2}(N)+{\rm{const.}},\end{eqnarray} \tag{ 31 }$$

with c being the central charge of the underlying conformal field theory, and the additive constant being non-universal and depending on n. For non-critical systems the correlation length ξ is finite, and finite-size corrections described by a universal function $s(N/\xi )$ need to be taken into account. Following [64], we assume a scaling behavior

$$\begin{eqnarray}&&S(N)\simeq \displaystyle \frac{c}{6}\;{\mathrm{log}}_{2}(N)-\displaystyle \frac{c}{6}\mathrm{ln}\left(\displaystyle \frac{N}{\xi }+{{\rm{e}}}^{-\alpha N/\xi }\right)+{\rm{const.}},\end{eqnarray} \tag{ 32 }$$

where the parameter α will be taken as 1. We will also fix n at the center of the chain, that is $n=(N+1)/2$, as we will focus on odd N. Equation (32) implies that S(N) saturates for finite ξ at sufficiently large N, while equation (31) implies a logarithmic divergence for critical systems.

Using the DMRG code implemented in the iTensor library [67], we have studied the ℓXY model for system sizes up to N = 327, with up to 200 states kept in a DMRG sweep. Instead of studying the full dipolar model, we have cut the long-range tail of the interactions, taking into account only nearest- and next-to-nearest interactions. For a fixed parameter ${J}_{2}/| {J}_{1}|$, we calculate S(N) for different magnetic field strengths B. From the behavior of S(N), we are able to determine the critical regions: up to a first critical field strength ${B}_{{\rm{c,1}}}$, the entanglement entropy takes a relatively small value and does not scale with N. This behavior indicates a vanishing correlation length, and agrees with the structure of the AP. For slightly larger values of B, the entanglement entropy still remains constant up to some value N, suggesting that sufficiently small systems still exhibit AP behavior, while larger systems already have FP behavior. For example, for ${J}_{2}/| {J}_{1}| =1$, we get ${B}_{{\rm{c,1}}}\approx 0.25| {J}_{1}|$, but AP behavior persists in systems of size N = 55 for field strengths up to $B=0.26| {J}_{1}|$, in systems of size N = 31 up to $B=0.27| {J}_{1}|$, and in systems as small as N = 11 even up to $B=0.5| {J}_{1}|$.

In the floating point regime, the scaling of S(N) is well described by equation (32), compatible with the expected central charge c = 1. Fitting our data to equation (32) yields a finite correlation length, plotted in figure 7. When B approaches a second critical value ${B}_{{\rm{c,2}}}$, the correlation length significantly increases, indicating quantum criticality in the vicinity of the FP–PM transition. For even larger values of $B\gt {B}_{{\rm{c,2}}}$, S(N) again becomes constant, though now in the limit of large N. This behavior is expected for a sufficiently large PM system, characterized by a small but finite correlation length.

Zoom In Zoom Out Reset image size

Qualitatively, the described behavior is found for different ${J}_{2}/| {J}_{1}|$. We have focussed on two values ${J}_{2}/| {J}_{1}| =0.8$ and ${J}_{2}/| {J}_{1}| =1$. In the former case, we obtain ${B}_{{\rm{c,1}}}=0.10| {J}_{1}|$ and ${B}_{{\rm{c,2}}}=0.45| {J}_{1}|$. In the latter case, we obtain ${B}_{{\rm{c,1}}}=0.25| {J}_{1}|$ and ${B}_{{\rm{c,2}}}=0.60| {J}_{1}|$. Remarkably, the extent of the FP along B, that is ${B}_{{\rm{c,2}}}-{B}_{{\rm{c,1}}}$, is the same for both parameters J₂, in agreement with earlier findings for the qANNNI model [64].

Finally let us turn our attention to the nearest-neighbor ℓXY model, which we have studied for ${J}_{2}/| {J}_{1}| =1$. We find the same behavior as before for the system with nearest and next-to-nearest interactions, but the critical field strengths ${B}_{{\rm{c,1}}}$ and ${B}_{{\rm{c,2}}}$ are shifted towards larger values (0.52 and 0.81 for ${J}_{2}/| {J}_{1}| =1$). The extent of the FP is slightly smaller than in the system with nearest-neighbor and next-nearest-neighbor interactions.

As a summary, our results suggest that, sufficiently far from the frustration point, the dipolar ℓXY model has no qualitative changes with respect to the qANNNI phase diagram. We find clear evidence for the PM to FM phase transition, as well as for the transition from the AP to the FP, even in small-sized systems. DMRG calculations for larger systems demonstrate that also the phase transition from the FP to the PM phase persists in the presence of interactions beyond nearest neighbors.

In this section, we want to show that the dual quantum simulator (15) can be used to explore the phase diagram of quantum Ising models with multi-spin interactions.

In order to achieve the desired Hamiltonian, we shall focus on a particular trapped-ion realization of the above scheme that uses two different hyperfine levels within the atomic ground state manifold to encode the pseudo-spin. In this case, the spin-dependent dipole forces (4) that couple to both radial phonon branches, ${F}_{i,n}^{\alpha }$ with $\alpha \in \{x,y\}$, arise from a combination of two-photon Raman transitions, each of which requires a pair of laser beams tuned far from the resonance of a dipole-allowed transition to an excited state [24]. If the effective wave vector of the interfering laser beams, ${\rm{\Delta }}{{\boldsymbol{k}}}^{\alpha }={{\boldsymbol{k}}}_{{\rm{L,1}}}^{\alpha }-{{\boldsymbol{k}}}_{{\rm{L,1}}}^{\alpha }$, has a component along the ion-trap axis, ${e}_{z}\cdot {\rm{\Delta }}{{\boldsymbol{k}}}^{\alpha }={\rm{\Delta }}{k}_{z}^{\alpha }\ne 0$, and the two-photon Raman transitions lie far away from the axial sidebands, one recovers the desired ℓXY model (1), but with modified spin–spin interactions (7), namely

$$\begin{eqnarray}&&{J}_{{ij}}^{\alpha }\approx \displaystyle \frac{{J}_{0}^{\alpha }\mathrm{cos}({\rm{\Delta }}{k}_{z}^{\alpha }({z}_{i}^{0}-{z}_{j}^{0}))}{| {z}_{i}^{0}-{z}_{j}^{0}{| }^{3}},\phantom{\rule{2ex}{0ex}}{J}_{0}^{\alpha }\gt 0,\phantom{\rule{2ex}{0ex}}\alpha \in \{x,y\}.\end{eqnarray} \tag{ 33 }$$

We thus obtain periodically modulated spin–spin interactions that still decay with a dipolar power law. By controlling the ion lattice spacing, or the direction of the laser beams, one can set ${\rm{\Delta }}{k}_{z}^{x}({z}_{i}^{0}-{z}_{i+1}^{0})=\frac{\pi (2m+1)}{2}$ for some integer $m\in {{\mathbb{Z}}}^{+}$, such that the nearest-neighbor spin–spin couplings are inhibited ${J}_{i,i+1}^{x}\approx 0$. The fulfilment of this condition requires an homogeneous lattice spacing in the ion crystal, which can be achieved by using micro-fabricated surface traps [30] or by segmenting the axial electrodes in linear Paul traps [68].

Under these conditions, we can rearrange the dual Hamiltonian (15) as follows ${H}_{{\ell }\mathrm{XY}}^{{\rm{dual}}}\ =\quad {H}_{{\rm{qIMS}}}(-h,{J}_{i,i+2}^{x},{J}_{i,i+1}^{y})$ $+{\rm{\Delta }}\tilde{H}$, where we have introduced the quantum Ising model with multi-spin interactions (qIMS), namely

$$\begin{eqnarray}&&{H}_{{\rm{qIMS}}}({\tilde{J}}_{2},{\tilde{J}}_{4},\tilde{B})=\displaystyle \sum _{i}({\tilde{J}}_{2}{\tau }_{i}^{z}{\tau }_{i+1}^{z}+{\tilde{J}}_{4}{\tau }_{i}^{z}{\tau }_{i+1}^{z}{\tau }_{i+2}^{z}{\tau }_{i+3}^{z}+B{\tau }_{i}^{x}).\end{eqnarray} \tag{ 34 }$$

Here, the Ising interaction ${\tilde{J}}_{2}\lt 0$ is a FM nearest-neighbor coupling that corresponds to the longitudinal field of the original Hamiltonian (1), ${\tilde{J}}_{4}\gt 0$ is an anti-ferromagnetic four-spin Ising coupling that corresponds to the next-nearest-neighbor XX couplings of the original model, and $\tilde{B}$ is a transverse magnetic field that corresponds to the nearest-neighbor YY couplings of the original model. This parameter equivalence under the duality transformation is

$$\begin{eqnarray}&&{\tilde{J}}_{2}=-h,\phantom{\rule{2ex}{0ex}}{\tilde{J}}_{4}={J}_{i,i+2}^{x},\phantom{\rule{2ex}{0ex}}\tilde{B}={J}_{i,i+1}^{y}.\end{eqnarray} \tag{ 35 }$$

Let us emphasize that the competition of the Ising interactions, characterized by ${\tilde{J}}_{4}/| {\tilde{J}}_{2}|$, corresponds to the ratio ${J}_{i,i+2}^{x}/h$ in the original model, which can be tuned to any particular value. The same occurs for the ratio $\tilde{B}/| {\tilde{J}}_{2}|$, which corresponds to ${J}_{i,i+1}^{y}/h$, such that the whole phase diagram of the qIMS can be addressed with the dual quantum simulator.

In addition to the qIMS Hamiltonian, the dipolar tail of the interactions leads to the following perturbation

$$\begin{eqnarray}&&\tilde{H}=\displaystyle \sum _{i=1}^{N+1}\displaystyle \sum _{j=i+3}^{N+1}{J}_{{ij}}^{x}{\tau }_{i-1}^{z}{\tau }_{i}^{z}{\tau }_{j-1}^{z}{\tau }_{j}^{z}+\displaystyle \sum _{i=1}^{N+1}\displaystyle \sum _{j=i+2}^{N+1}{J}_{{ij}}^{y}\displaystyle \prod _{i\leqslant k\lt j}{\tau }_{k}^{x},\end{eqnarray} \tag{ 36 }$$

where some of the couplings also vanish due to the periodic modulation (33), namely ${J}_{{ij}}^{x}\approx 0$ for all $j=i+(2m+1)$ with $m\in {{\mathbb{Z}}}^{+}$. Due to the fast dipolar decay (33), one can argue once more that this perturbation will not modify in any essential manner the phase diagram of the qIMS model (34), such that the dual quantum simulator (15) also gives access to the physics of these exotic quantum magnets.

In the absence of four-body couplings ${\tilde{J}}_{4}=0$, this model (34) corresponds to the standard quantum Ising model [7], displaying a second-order phase transition at ${\tilde{J}}_{2}=\tilde{B}$ in the Ising universality class [4]. In the absence of pair-wise couplings ${\tilde{J}}_{2}=0$, the model corresponds to the quantum-mechanical version of a classical Ising model in a square lattice [69] describing stacked Ising chains with four-body couplings at finite temperatures, as can be proved by applying the quantum-classical mapping [5] in the present case [70, 71]. The model has a ${{ \mathcal Z }}_{2}\times {{ \mathcal Z }}_{2}\times {{ \mathcal Z }}_{2}$ symmetry (i.e. cartesian product of spin inversions for the 3 different spin pairs in each four-site partition of the lattice), which leads to an eight-fold degenerate ground state for $\tilde{B}=0$, and a first-order phase transition at ${\tilde{J}}_{4}=\tilde{B}$ in the universality class of the q = 8 Potts model [72]. As occurred for the qANNNI model (18), one thus expects that the competition of both Ising interactions, and their interplay with the quantum fluctuations brought by the transverse field, must lead to very interesting critical phenomena. In contrast to the frustrated Hamiltonian, this quantum multi-spin Ising model has not been studied in such detail. FSS studies with up to N = 16 spins already point towards very interesting critical phenomena: The nature of the quantum phase transitions as a function of $\tilde{B}$ changes from first to second order around ${\tilde{J}}_{4}/| {\tilde{J}}_{2}| =1/2$ [73]. However, the limited finite sizes did not allow for accurate studies close to the interesting point ${\tilde{J}}_{4}/| {\tilde{J}}_{2}| =1/2$, which classically $\tilde{B}=0$ leads to a largely degenerate ground state that can give rise to a variety of phases upon switching the transverse magnetic field. We believe that a more careful analysis of this region would be very interesting, and we hope that this manuscript will stimulate future work in that direction.

From the experience gained by the exhaustive numerical study of the previous section, we conjecture that the quantum simulator of the quantum Ising model with multi-site interactions (34) will not be compromised by the additional dipolar tail (36), such that the above interesting region can be characterized experimentally using the accessible non-local order parameters (16), or the FSS of other spectroscopic observables, characteristic of current ion-trap experiments.

In this manuscript, we have presented an alternative route to build quantum simulators of exotic magnetism by exploiting the notion of quantum dualities. In certain situations, such as the ones discussed in this work, such duality transformations allow one to explore interesting models that involve frustration or multi-spin interactions, and their interplay with quantum fluctuations, by focusing on different spin models that are simpler to implement in a particular experimental platform. This dual approach has one important caveat: measurements of highly non-local observables should be feasible in the particular experiment. This makes trapped-ion setups ideally suited for this playground of dual quantum simulation.

We have focused on two particular dual quantum simulators which can be implemented using state-of-the-art technology in linear ion crystals, and which allow one to explore paradigmatic models of frustration: the quantum axial nearest-neighbor Ising model, and the quantum Ising model with competing 2- and 4-body interactions. In the former case, we have made a careful numerical study to prove the validity of our scheme, which takes into account relevant perturbations that occur naturally in the trapped-ion scenario.

Although we have focused on these two particular examples for ion chains, the notion of dual quantum simulators can be certainly applied to other models, such as the quantum spin liquids, topologically ordered phases, or Ising lattice gauge theories mentioned in the introduction. Provided that quantum magnets are finally synthesized in Penning or surface traps, this quantum-duality approach will also become relevant for other lattice geometries, which may define an alternative route to these exotic quantum many-body phenomena.

Finally, let us mention that in the recent years another platform for long range spin models has been proposed, namely ultracold atoms in nanostructures, or more precisely ultracold atoms trapped in a vicinity of tapered fibers and optical crystals (band gap materials). The experimental progress in coupling of ultracold atomic gases to nanophotonic waveguides is very rapid (for a recent review see [74]). The ideas and proposals concerning realization of long range spin models were developed for instance in [75–77], and it would be interesting to explore the possibilities of quantum dualities in this context.

We acknowledge discussions with Andrew Ferris, Luca Tagliacozzo, and Shi Ju Ran. A B acknowledges support from Spanish Mineco Project FIS2012-33022, and the CAM Research Network QUITEMAD+. TG and ML acknowledge support from EU grants OSYRIS (ERC-2013-AdG Grant No. 339106), SIQS (FP7-ICT-2011-9 No. 600645), QUIC (H2020-FETPROACT-2014 No.641122), EQuaM (FP7/2007-2013 Grant No. 323714), Spanish MINECO grants (Severo Ochoa Grant SEV-2015-0522 and FOQUS FIS2013-46768), Generalitat de Catalunya grant SGR 874, and Fundació Cellex.