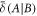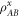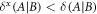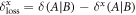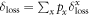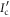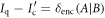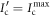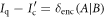Abstract
The benefits of entanglement can outlast entanglement itself. In quantum illumination, entanglement is employed to better detect reflecting objects in environments so noisy that all entanglement is destroyed. Here, we show that quantum discord—a more resilient form of quantum correlations—explains the resilience of quantum illumination. We introduce a quantitative relation between the performance gain in quantum illumination and the amount of discord used to encode information about the presence or absence of a reflecting object. This highlights discords role preserving the benefits of entanglement in entanglement breaking noise.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Quantum illumination [1–6] offers a radical departure from conventional quantum protocols [7, 8]. Most quantum technologies require fragile entangling correlations to be preserved, whereas quantum illumination operates in extremely adverse environments with entanglement-breaking noise [9, 10]. Specifically, quantum illumination aims to detect a low reflective target basked in bright noise by probing it with one arm of an entangled state. The protocol demonstrates significant improvement over the use of conventional probes, even though the environmental noise destroys all initial entanglement [1, 2]. This counter-intuitive phenomenon has been recently realized in a series of experiments [11–13].
The absence of entanglement, however, does not necessarily imply classicality. Quantum protocols that operate with negligible entanglement exist [14, 15], motivating the search for quantum resources beyond entanglement. Quantum discord is a prominent candidate [16–18]. Initially proposed to isolate the 'quantum' component of mutual information between two physical systems, discord is conjectured to be a potential quantum resource, responsible for the advantage of certain quantum algorithms [19]. While promising advances have been made in understanding the operational significance of discord [20–28], this remains a topic of significant debate. Contrary to entanglement, which is difficult to synthesize, discord is non-zero for almost every mixed state [29] and its practical merit conflicts with the preconception that 'quantum' effects are fragile.
In this paper, we show that it is precisely the resilience of discord that explains the resilience of quantum illumination and highlight discord's role in preserving entanglement's benefits in quantum illumination. We first investigate what resources remain in illumination, after entanglement is broken by the environment. We then show that discord survives, and the quantum illumination makes use of this surviving discord to preserve information about the potential presence of a reflecting object that would otherwise be lost. We find that the amount of discord associated with sensing the target coincides exactly with the performance gain of quantum illumination over the best conventional technique.
2. Framework
Illumination aims to discern whether a weakly reflecting object is present or absent in a distant region of intense noise (see figure 1). This can be viewed as a task in information retrieval. A distant region of space contains a bit of information that dictates the presence (x = 0) or the absence (x = 1) of the object. From this point of view, the goal of illumination is to retrieve the value x of a random variable 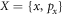 with binary alphabet
with binary alphabet  .
.
Figure 1. A premise of illumination. In conventional illumination, a single probe is sent into a noisy region to detect the presence of a potential object. (a) If the object is present, there is a small chance a reflected signal is detected; otherwise (b) the probe is completely lost and Alice just sees only random noise. In quantum illumination (c)–(d), Alice prepares two maximally entangled systems, one is kept (idler) and the other sent for target detection (signal). The reflected signal and idler are finally detected by a joint measurement. Surprisingly, the use of an entangled source yields better performance, even though entanglement fails to survive the return trip.
Download figure:
Standard image High-resolution imageIn the conventional approach, Alice probes the distant region with a suitable quantum system (where suitable implies a system that the reflector would potentially reflect), and monitors for a potential reflection. Let the probe be a d-dimensional quantum system, i.e, a qudit, in a pure state  . If the reflector is absent (x = 1), the entirety of Φ is lost and Alice retrieves random environmental noise described by a maximally mixed state
. If the reflector is absent (x = 1), the entirety of Φ is lost and Alice retrieves random environmental noise described by a maximally mixed state 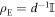 , where
, where 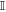 is the identity operator. Otherwise (x = 0), the reflector may reflect the object back at Alice; and the noise
is the identity operator. Otherwise (x = 0), the reflector may reflect the object back at Alice; and the noise  Alice observes is biased by the signal Φ with some small weighting
Alice observes is biased by the signal Φ with some small weighting  . Thus, probing the the reflector corresponds to encoding
. Thus, probing the the reflector corresponds to encoding  into the output codewords
into the output codewords
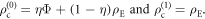
By detecting the reflected qudit, Alice has a limited ability to distinguish these states and, therefore, to infer the value of x.
In quantum illumination, Alice improves her strategy by resorting to quantum correlations. She prepares a maximally entangled state 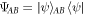 of two qudits A and B, where
of two qudits A and B, where 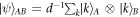 , with
, with  being an orthonormal basis. Then, she probes the target with the signal system A while retaining the idler system B in a quantum memory (or just a delay line in experimental settings). Now we have encoded the value of X via two codewords
being an orthonormal basis. Then, she probes the target with the signal system A while retaining the idler system B in a quantum memory (or just a delay line in experimental settings). Now we have encoded the value of X via two codewords
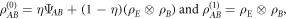
where 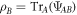 represents the reduced state of the idler if the signal is completely lost.
represents the reduced state of the idler if the signal is completely lost.
In either approach, Alice ends up in possession of one of two potential codewords, 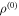 or
or 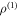 , depending on x. The better Alice can discriminate between these codewords, the more information she can access about x. Quantum illumination thus outperforms its conventional counterpart when it is easier to distinguish
, depending on x. The better Alice can discriminate between these codewords, the more information she can access about x. Quantum illumination thus outperforms its conventional counterpart when it is easier to distinguish 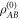 from
from 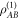 , than
, than 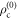 from
from  , for any conventional input Φ.
, for any conventional input Φ.
To capture this quantity mathematically, consider first the general scenario where information about X is encoded within a quantum system S; such that S takes on the value  when X = x. Let this encoding be captured by the ensemble
when X = x. Let this encoding be captured by the ensemble 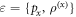 , and I be the amount of information about X that Alice can access when given ε. That is, Alice is challenged to announce an estimate of x,
, and I be the amount of information about X that Alice can access when given ε. That is, Alice is challenged to announce an estimate of x, 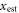 , governed by random variable Xest. Her performance is dictated by the maximum
, governed by random variable Xest. Her performance is dictated by the maximum 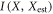 Alice can achieve, when supplied with
Alice can achieve, when supplied with 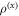 .
.
To evaluate I, observe that in order to retrieve information about x, Alice must measure some general positive operator value measurement (POVM) 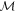 on S, whose output defines another random variable
on S, whose output defines another random variable 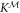 that is used by Alice to generate Xest. Alice's optimal performance thus aligns with the mutual information between X and the measured output
that is used by Alice to generate Xest. Alice's optimal performance thus aligns with the mutual information between X and the measured output 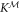 , when maximized over all possible measurements
, when maximized over all possible measurements 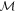
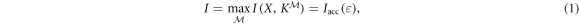
where 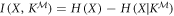 and
and  denote's Alice's accessible information about X with respect to ε. When X is uniformly distributed,
denote's Alice's accessible information about X with respect to ε. When X is uniformly distributed, 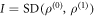 , where
, where 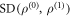 is a well studied distinguishably measure known as the the Shannon distinguishably of
is a well studied distinguishably measure known as the the Shannon distinguishably of 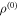 and
and  .
.
Applying this result, the performance of quantum illumination is then given by 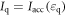 , where
, where  . On the other hand, the optimal performance achievable in conventional illumination is provided by maximizing the accessible information with respect to the ensemble
. On the other hand, the optimal performance achievable in conventional illumination is provided by maximizing the accessible information with respect to the ensemble 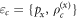 over all input states Φ, i.e.,
over all input states Φ, i.e., 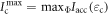 . The difference
. The difference  thus quantifies the advantage of quantum illumination—in terms of the amount of extra information Alice can gain about x in a single trial. In the case of uniform X,
thus quantifies the advantage of quantum illumination—in terms of the amount of extra information Alice can gain about x in a single trial. In the case of uniform X,  is reduced to the gain in Shannon distinguishingly between codewords, when quantum methods are adopted over best conventional probes. While these quantities are generally very difficult to compute, the commutativity of the codewords makes the problem tractable for the special case of illumination (see the appendix).
is reduced to the gain in Shannon distinguishingly between codewords, when quantum methods are adopted over best conventional probes. While these quantities are generally very difficult to compute, the commutativity of the codewords makes the problem tractable for the special case of illumination (see the appendix).
We note that several other methods to characterize the benefits of quantum illumination exist in literature. The quantifier introduced by Lloyd [1], for example, is based on the probability of guessing x correctly. The performance measures are closely related: knowledge of one bounds the other from both above and below, and the scaling properties of the two measures coincide [30]. In using information theoretic quantifiers of distinguishability, we have followed an approach similar to that of quantum reading [34–36], where the mutual information was used to better characterize the optimal readout of a classical memory.
Noise resilience. The distinguishing feature of quantum illumination is that it exhibits a performance advantage even in scenarios where 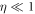 , and
, and 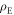 is completely mixed. This counters conventional intuition; the intense noise implies that
is completely mixed. This counters conventional intuition; the intense noise implies that 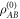 and
and 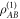 are both highly entropic and completely separable, despite the use of a maximally entangled probe
are both highly entropic and completely separable, despite the use of a maximally entangled probe  . This peculiarity is highlighted when we recast quantum illumination into a functionally equivalent quantum circuit, where the action of the noise is separated from that of the reflecting object (see figure 2). Irrespective of whether the reflector is present, the noise decoheres Alice's input
. This peculiarity is highlighted when we recast quantum illumination into a functionally equivalent quantum circuit, where the action of the noise is separated from that of the reflecting object (see figure 2). Irrespective of whether the reflector is present, the noise decoheres Alice's input 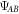 into the separable state
into the separable state 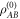 (see figure 2(c)). Now the presence or absence of the target, i.e., the value x of the random variable X, is encoded into the state by applying the operator
(see figure 2(c)). Now the presence or absence of the target, i.e., the value x of the random variable X, is encoded into the state by applying the operator 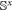 to the signal system, with
to the signal system, with 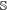 being the swap operator between the signal and environment (see figure 2(b)).
being the swap operator between the signal and environment (see figure 2(b)).
This viewpoint suggests that there must still exist some form of 'quantumness' after noise injection; that is, we expect some form of quantum correlations to survive in the separable state  and that these correlations are related to quantum illumination's superior performance. Here, we demonstrate a direct relation between the discord remaining in
and that these correlations are related to quantum illumination's superior performance. Here, we demonstrate a direct relation between the discord remaining in 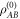 and the performance advantage in illumination,
and the performance advantage in illumination, 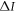 .
.
3. The role of discord
Formally, the discord of the signal-idler system, denoted as 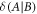 , quantifies the discrepancy between two types of correlations [18]. The first type is the quantum mutual information
, quantifies the discrepancy between two types of correlations [18]. The first type is the quantum mutual information 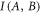 which accounts for the total correlations between the two systems A and B. The second type, denoted by
which accounts for the total correlations between the two systems A and B. The second type, denoted by  , quantifies the classical correlations and equals the maximal entropic reduction of system A under POVM measurements
, quantifies the classical correlations and equals the maximal entropic reduction of system A under POVM measurements 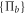 on system B. Explicitly, this is defined by optimizing over all POVMs as
on system B. Explicitly, this is defined by optimizing over all POVMs as 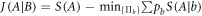 , where S(A) is the von Neumann entropy of system A and
, where S(A) is the von Neumann entropy of system A and  is the entropy of system A given the outcome b, achieved with probability pb. The discord
is the entropy of system A given the outcome b, achieved with probability pb. The discord 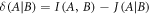 between A and B captures the discrepancy between the two measures.
between A and B captures the discrepancy between the two measures.
As aforementioned, quantum illumination can operate when 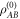 (the state that is responsible for sensing the target according to the equivalent quantum circuit in figure 2)—contains discord but no entanglement. In order to convince ourselves that this is more than just coincidental, we need to establish a quantitative relation between the discord that persists after noise injection, and the quantum advantage
(the state that is responsible for sensing the target according to the equivalent quantum circuit in figure 2)—contains discord but no entanglement. In order to convince ourselves that this is more than just coincidental, we need to establish a quantitative relation between the discord that persists after noise injection, and the quantum advantage 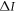 . To do this, we draw inspiration from the concept of 'discord consumption' that was used to highlight how discord can be interpreted as a resource that can be accessed via coherent interactions.
. To do this, we draw inspiration from the concept of 'discord consumption' that was used to highlight how discord can be interpreted as a resource that can be accessed via coherent interactions.
Figure 2. Operationally equivalent circuit model of illumination. Quantum illumination can be understood in the quantum circuit picture. Let (a) and (b) denote respectively the operationally equivalent circuits for the presence (x = 0) and absence (x = 1) of the reflecting object. (a) is modeled by mixing 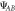 with environmental noise
with environmental noise 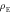 , resulting in state
, resulting in state 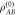 . In (b), the complete loss of signal is represented by a SWAP operation
. In (b), the complete loss of signal is represented by a SWAP operation 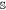 between the signal system and environment. In either scenario, the resulting quantum channel is entanglement-breaking. The two scenarios can combine into a single circuit (c), composed of two sequential stages. In stage (i), environmental noise is injected into the signal arm by mixing in
between the signal system and environment. In either scenario, the resulting quantum channel is entanglement-breaking. The two scenarios can combine into a single circuit (c), composed of two sequential stages. In stage (i), environmental noise is injected into the signal arm by mixing in  , resulting in the state
, resulting in the state 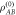 . In (ii), the presence or absence of the target can be modeled as encoding the binary variable X onto
. In (ii), the presence or absence of the target can be modeled as encoding the binary variable X onto 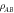 by applying
by applying 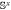 , where
, where 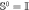 is the identity.
is the identity.
Download figure:
Standard image High-resolution imageDiscord expenditure. Consider first a related scenario where Alice begins with a bipartite quantum state 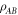 with discord
with discord 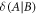 as a resource. Alice encodes some x, governed by random variable X, by applying an x-dependent local unitary operation,
as a resource. Alice encodes some x, governed by random variable X, by applying an x-dependent local unitary operation,  , on A; resulting in codewords
, on A; resulting in codewords 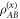 . To a third party unaware of which x is encoded, the resulting state is
. To a third party unaware of which x is encoded, the resulting state is  . Let
. Let 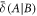 be the discord of state
be the discord of state 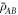 . The difference
. The difference 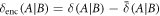 represents the reduction in discord from the perspective of a third party Bob, who is unaware of which x was selected. In prior literature, this is regarded as the amount of discord consumed to encode X, or alternatively, the amount of information about X that is encoded within discord correlations [24].
represents the reduction in discord from the perspective of a third party Bob, who is unaware of which x was selected. In prior literature, this is regarded as the amount of discord consumed to encode X, or alternatively, the amount of information about X that is encoded within discord correlations [24].
In the above scenario, the transformation from initial resources to codewords used only local unitary operators on A. The discord of every individual codeword coincided with the discord of the original resource. Thus, no discord was lost to the environment during the encoding process. In illumination, this is no longer the case and we need to account for this extra loss as outlined by figure 3. We make the following observations
- (1)The amount of discord between signal and idler after noise injection is
 . This can be regarded as the amount of discorded resources we have prior to encoding.
. This can be regarded as the amount of discorded resources we have prior to encoding. - (2)The amount of discord after sensing the object is
 (for someone who does not know the value of X).
(for someone who does not know the value of X). - (3)If a particular codeword
 has discord
has discord  , then the encoding of x is not discord preserving. In this case, we lose
, then the encoding of x is not discord preserving. In this case, we lose  units of discord. This discord is not used to encode x.
units of discord. This discord is not used to encode x. - (4)The average loss is then given by
 .
.
Figure 3. Discord flow in illumination. (a) Quantum illumination begins with a maximally entangled state with a discord value of 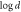 . (b) The injection of noise destroys all entanglement within the system producing a noisy state
. (b) The injection of noise destroys all entanglement within the system producing a noisy state 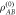 which retains
which retains 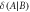 units of discord. This represents the resources we effectively have available for sensing the target. (c) During the encoding stage, the swap gate
units of discord. This represents the resources we effectively have available for sensing the target. (c) During the encoding stage, the swap gate 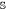 is applied with probability p1, which leaks an average of
is applied with probability p1, which leaks an average of  units of discord into the environment, leaving
units of discord into the environment, leaving 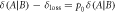 units of discord available for encoding the value of X. (d) The encoding protocol then splits off
units of discord available for encoding the value of X. (d) The encoding protocol then splits off 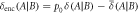 to store extra information about x. (e) The remaining
to store extra information about x. (e) The remaining 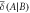 units of discord are not expended during the encoding protocol, and could be used to encode other information at some stage in the future.
units of discord are not expended during the encoding protocol, and could be used to encode other information at some stage in the future.
Download figure:
Standard image High-resolution imageFigure 4. Advantage and discord in qubit illumination. (a) Quantum illumination (black dashed line) outperforms the best conventional methods (green solid line) for all non-zero values of η. (b) Entanglement of formation of the signal-idler system is zero for 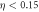 (blue dashed line). Discord, however, is present for all values of η (dashed red line), and the amount of discord expended to encode x (blue solid line),
(blue dashed line). Discord, however, is present for all values of η (dashed red line), and the amount of discord expended to encode x (blue solid line),  , coincides exactly with the performance gain of quantum illumination,
, coincides exactly with the performance gain of quantum illumination,  , i.e., the shaded region in (a).
, i.e., the shaded region in (a).
Download figure:
Standard image High-resolution imageIn illumination 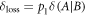 as all
as all 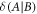 units of discord are lost if the reflecting object is absent. Factoring in this loss, we see that the amount of discord that is actually used to encode x is given by
units of discord are lost if the reflecting object is absent. Factoring in this loss, we see that the amount of discord that is actually used to encode x is given by
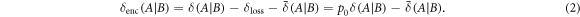
This generalizes the concept of discord expended to encode the variable x to the case of illumination. We can see that the only difference between this and the case of unitary encodings is the extra factor of p0, representing that in illumination, only p0 of the discorded resources before encoding are useful. Meanwhile, it shares the property that  . The amount of discord associated with encoding x is always abounded above by the amount of discord resources initially available. It is also interesting to note that
. The amount of discord associated with encoding x is always abounded above by the amount of discord resources initially available. It is also interesting to note that 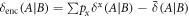 . That is,
. That is, 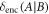 , can also be interpreted the gain in discord between signal and when someone learns the value of x.
, can also be interpreted the gain in discord between signal and when someone learns the value of x.
Relation to the quantum advantage. The advantage of quantum illumination coincides exactly with the discord expended for encoding x, that is
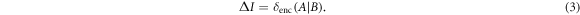
The key idea behind our argument is as follows: we introduce an additional constraint to the quantum illumination protocol and show that
- (i)The optimal performance of quantum illumination, subject to this constraint,
 , coincides with the best performance using conventional illumination
, coincides with the best performance using conventional illumination  .
. - (ii)The loss in performance in enforcing this constraint over quantum illumination is
 .
.
Specifically, the constraint imposes a specific measurement procedure Alice must use to extract x upon receipt of 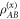 . Instead of allowing for arbitrary measurements, she is required to first make a local measurement on the idler B, followed by a local measurement on the signal A. (i) Implies that this restricted procedure is operational equivalent to classical illumination, and (ii) implies that the loss of performance due to this restriction exactly coincides with the discord used to encode x. Together, the two statements imply the main result, i.e.,
. Instead of allowing for arbitrary measurements, she is required to first make a local measurement on the idler B, followed by a local measurement on the signal A. (i) Implies that this restricted procedure is operational equivalent to classical illumination, and (ii) implies that the loss of performance due to this restriction exactly coincides with the discord used to encode x. Together, the two statements imply the main result, i.e.,  . Details, including proofs of (i) and and (ii) are available in the appendix.
. Details, including proofs of (i) and and (ii) are available in the appendix.
These results reveal why quantum illumination is advantageous, and how discord plays a role. In Gu et al[24], it was established that information encoded within discorded correlations of two objects, A and B, represents information that can only be extracted through coherent interactions between A and B. Here, (i) indicates that  represents information about x that is encoded within discorded correlations, while (ii) demonstrates that quantum illumination derives it advantage by using coherent interactions between idler and probe to access this information.
represents information about x that is encoded within discorded correlations, while (ii) demonstrates that quantum illumination derives it advantage by using coherent interactions between idler and probe to access this information.
As a result, quantum illumination gives an advantage  only if the effective state
only if the effective state 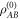 generated by the environment has non-zero discord, and the corresponding quantum advantage
generated by the environment has non-zero discord, and the corresponding quantum advantage 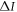 is directly provided by the amount of discord
is directly provided by the amount of discord 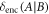 associated with storing information about the presence and absence of the target. This identifies that discord plays a key role behind the resilience of quantum illumination, providing an extra resource in which information about the target is stored. While entanglement does not survive in quantum illumination, the survival of discord is essential for it to have any advantage over conventional illumination.
associated with storing information about the presence and absence of the target. This identifies that discord plays a key role behind the resilience of quantum illumination, providing an extra resource in which information about the target is stored. While entanglement does not survive in quantum illumination, the survival of discord is essential for it to have any advantage over conventional illumination.
4. A simple example
We illustrate the equivalence of equation (3) in the case where signal and idler are two-level quantum systems, i.e., qubits. The environment is flooded with random qubits, such that 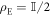 . For example, this may model the detection of a multi-faceted, rotating, object in noise [1].
. For example, this may model the detection of a multi-faceted, rotating, object in noise [1].
The conventional approach probes the target with a pure state 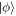 , returning either
, returning either  or
or  (any pure input state gives the same performance). In quantum illumination, Alice instead probes the target with one of arm of the Bell state
(any pure input state gives the same performance). In quantum illumination, Alice instead probes the target with one of arm of the Bell state 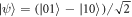 or any other maximally entangled state. This results in codewords,
or any other maximally entangled state. This results in codewords, 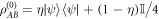 and
and 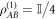 . The corresponding performances of conventional and quantum illumination,
. The corresponding performances of conventional and quantum illumination, 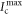 and Iq, respectively, are plotted versus the target reflectivity η in figure 3(a) for the case where X is distributed unformly. The difference between these curves (shaded region) quantifies the gain
and Iq, respectively, are plotted versus the target reflectivity η in figure 3(a) for the case where X is distributed unformly. The difference between these curves (shaded region) quantifies the gain 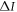 of quantum illumination.
of quantum illumination.
As we can see from figure 3(b), the state of the system after noise, 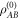 , is always separable for sufficiently small values of η. Nevertheless,
, is always separable for sufficiently small values of η. Nevertheless,  contains discord, part of which can be harnessed to store information about x. In comparing figure 3(a) with figure 3(b), we see that the amount of discord expended for resolving the target
contains discord, part of which can be harnessed to store information about x. In comparing figure 3(a) with figure 3(b), we see that the amount of discord expended for resolving the target 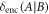 coincides exactly with the advantage
coincides exactly with the advantage 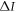 of quantum illumination.
of quantum illumination.
5. Discussion
In this paper, we have shown that discord underlies the resilience of quantum illumination in entanglement-breaking noise. In such situations, discord can survive when entanglement does not. Quantum illumination exploits these surviving quantum correlations to encode extra information regarding the potential presence of a reflective object. The amount of discord used to encode this information is shown to coincide exactly with the enhanced performance of quantum illumination, the equivalence holding for systems of arbitrary dimensions. This connection explains why the benefits of entanglement may survive entanglement-breaking noise, and helps establish discord's role in noise resilient quantum technology. The results in this manuscript are valid for general distributions of X. Thus our arguments apply to cases where one repeats the protocol multiple times to gain progressively more information about X. This can be modeled through Bayesian update, where the prior for X is updated with each successive trial.
In deriving our results, we quantified both the discord between signal and idler, and the performance advantage of quantum illumination via entropic measures. There are, of course, many other ways to measure either quantify (e.g. geometric measures of discord, increased success probabilities to measure performance advantage) and one may well be able to obtain similar relations between suitable alternative measures. Indeed, considerations of other performance measures for illumination may well motivate new operational measures of discord, much as consideration of phase estimation motivated interferometric power [27].
The techniques featured may also be generalized to related situations, such as encoding and communicating information when applying more general quantum operations in intense entanglement-breaking noise. This could lend insight to discord's role in cryptographic variants of illumination [12, 32, 33]. Our analysis also have potential to generalize to the continuous variable regime, though the non-commutativity of the resulting codewords may make direct analytical approaches. If so though, it will complement concurrent approaches to understand continuous quantum illumination's operational advantage using mutual information [38].
More generally, illumination belongs to a broader collection of protocols aimed to determine certain properties of unknown quantum channels, including quantum channel discrimination, quantum loss detection, and quantum metrology. In each of these protocols, numerical links between discord and performance have been proposed [19, 37, 39]. A similar approach to understanding how discord's role in preserving information in more general bipartite encodings could further formalize discord's influence in such scenarios, and lead to a unified, information theoretic understanding of how the benefits of entanglement survive when entanglement dies.
Acknowledgments
We would like to thank Si-Hui Tan, Ping Koy Lam, Syed Assad, Thomas Symul, Marco Piani, and Jing Yan Haw for discussions. We also gratefully acknowledge the National Research Foundation of Singapore (NRF), NRF-Fellowship (Reference No: NRF-NRFF2016-02), the Ministry of Education in Singapore, the Academic Research Fund Tier 3 MOE2012-T3-1-009; the Leverhulme Trust, the Engineering and Physical Sciences Research Council (EPSRC) Grant EP/L011298/1, the National Natural Science Foundation of China Grant 11450110058, and the John Templeton Foundation Grant 53914 'Occam's Quantum Mechanical Razor: Can Quantum theory admit the Simplest Understanding of Reality?' for funding this research.
Appendix. Proof of supporting statements
This section provides detailed proof of the two supporting statements. Recall that we introduced a variant of quantum illumination; where Alice's choice how to estimate x when given 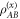 is constrained: Alice is required to first make a local measurement on the idler B, followed by a local measurement on the signal A. Let
is constrained: Alice is required to first make a local measurement on the idler B, followed by a local measurement on the signal A. Let 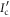 be the the optimal performance of this strategy. That is, Alice uses the above strategy to obtain Xest, an estimate of X. Let
be the the optimal performance of this strategy. That is, Alice uses the above strategy to obtain Xest, an estimate of X. Let 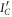 be be the maximum
be be the maximum 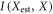 that can be achieved using the above strategy.
that can be achieved using the above strategy.
Here we prove the two supporting statements
- (i)The optimal performance of quantum illumination, subject to the restriction of measure the idler first, followed by measurement of the signal, coincides with the best performance using conventional illumination
 .
. - (ii)The loss in performance in using this third approach over quantum illumination is
 .
.
The detailed proofs of (i) and (ii) are below. Together, they imply that the main result, i.e., 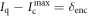
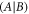 .
.
Proof of Statement (i). Recall that in the conventional approach, Alice probes for the reflecting object with a pure qudit state 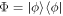 . The target-variable X is then mapped into the output codewords
. The target-variable X is then mapped into the output codewords

with associated ensemble 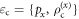 . Alice's optimal performance Ic is then given by,
. Alice's optimal performance Ic is then given by,  , the accessible information about X with respect to the ensemble
, the accessible information about X with respect to the ensemble 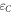 . Since the two codewords commute, this is equal to the Holevo information of communicating x using
. Since the two codewords commute, this is equal to the Holevo information of communicating x using 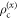 as codewords. That is, Alice's performance for a particular probe Φ is
as codewords. That is, Alice's performance for a particular probe Φ is
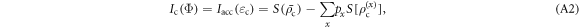
where 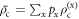 is the output state averaged over codewords, and
is the output state averaged over codewords, and  the von Neumann entropy. The optimal conventional performance is given by the optimization
the von Neumann entropy. The optimal conventional performance is given by the optimization  over all possible pure states Φ.
over all possible pure states Φ.
Note that we are restricting such an optimization to pure states, since mixed states surely provide worse performance. This can be explicitly proven by reductio ad absurdum. Assume that there exists some mixed state 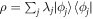 such that
such that 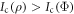 for all pure Φ. Then, let
for all pure Φ. Then, let 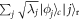 be a purification of ρ, where r denotes a reference system. If we had access to r, we can measure it in the
be a purification of ρ, where r denotes a reference system. If we had access to r, we can measure it in the  basis. This would collapse the probe state to
basis. This would collapse the probe state to 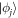 with probability
with probability  , resulting in an average performance of
, resulting in an average performance of 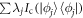 . In comparison, if the measurement result was lost, our performance would reduce to
. In comparison, if the measurement result was lost, our performance would reduce to 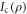 . Clearly, since performance can only degrade upon loss of information
. Clearly, since performance can only degrade upon loss of information
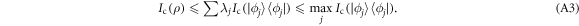
Therefore, there is a pure state  for some j such that
for some j such that 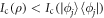 , which contradicts our initial assumption. Hence Ic must attain its maximum on a pure state.
, which contradicts our initial assumption. Hence Ic must attain its maximum on a pure state.
It is now important to note that, since 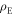 is completely mixed, symmetry considerations imply that
is completely mixed, symmetry considerations imply that 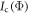 is the same for any pure state Φ, i.e., all pure probes deliver equal performance, and this performance coincides with the best possible performance of conventional illumination
is the same for any pure state Φ, i.e., all pure probes deliver equal performance, and this performance coincides with the best possible performance of conventional illumination 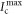 . This is a simple consequence of the invariance of the Holevo information under unitaries. In fact, let us apply an arbitrary unitary U to the codewords
. This is a simple consequence of the invariance of the Holevo information under unitaries. In fact, let us apply an arbitrary unitary U to the codewords 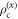 just before detection. Since
just before detection. Since  is proportional to the identity, we have
is proportional to the identity, we have

and 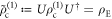 . These two codewords can equivalently be generated if we had started from the input state
. These two codewords can equivalently be generated if we had started from the input state  , which spans all the Hilbert space by varying U. At the same time, we note that the Holevo information does not change, i.e., for any U we have
, which spans all the Hilbert space by varying U. At the same time, we note that the Holevo information does not change, i.e., for any U we have
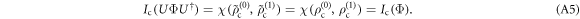
Thus, find that  for an arbitrary pure state Φ.
for an arbitrary pure state Φ.
To demonstrate that the optimal conventional performance 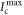 coincides with
coincides with 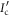 , we observe that all operations in the quantum illumination circuit commutes with a local measurement on the idler system B. Thus, there is no functional difference between measuring the idler beam after receipt of the reflected signal and measuring the same idler beam prior to sending out the signal.
, we observe that all operations in the quantum illumination circuit commutes with a local measurement on the idler system B. Thus, there is no functional difference between measuring the idler beam after receipt of the reflected signal and measuring the same idler beam prior to sending out the signal.
Then, suppose that Alice detects the idler system before transmission, by applying a rank-1 POVM 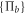 on the B-part of the maximally entangled state
on the B-part of the maximally entangled state 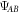 . Given an outcome b, with probability qb, the signal system A is collapsed into a conditional pure state
. Given an outcome b, with probability qb, the signal system A is collapsed into a conditional pure state 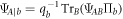 (this because rank-1 POVMs project pure states into pure states). Sending any pure probe
(this because rank-1 POVMs project pure states into pure states). Sending any pure probe 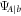 attains the maximum conventional performance
attains the maximum conventional performance 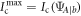 . On average, the performance of Alice is therefore given by
. On average, the performance of Alice is therefore given by
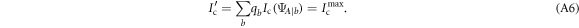
Proof of Statement (ii). Suppose that Alice performs the quantum illumination protocol by probing the target with the A-part of a maximally entangled state  . The target-variable
. The target-variable  is then mapped into the codewords
is then mapped into the codewords
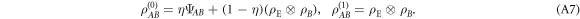
with associated emsemble 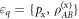 . Let be the maximum amount of information that Alice retrieves about the target-variable X using arbitrary quantum measurements, then
. Let be the maximum amount of information that Alice retrieves about the target-variable X using arbitrary quantum measurements, then 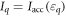 , the accessible information about X with respect to
, the accessible information about X with respect to 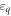 . It is easy to check that, for
. It is easy to check that, for 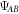 maximally entangled and
maximally entangled and 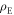 maximally mixed,
maximally mixed, ![$[{\rho }_{{AB}}^{(0)},{\rho }_{{AB}}^{(1)}]=0$](https://content.cld.iop.org/journals/1367-2630/18/4/043027/revision1/njpaa135eieqn171.gif) . Thus,
. Thus,  is equal to the Holevo information, i.e.,
is equal to the Holevo information, i.e.,
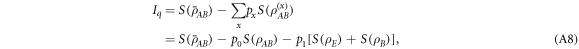
where 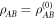 and
and  .
.
As before, let us consider 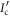 , defined as the maximum accessible information on X when Alice is constrained to measure the idler before sending the signal. Here we prove that
, defined as the maximum accessible information on X when Alice is constrained to measure the idler before sending the signal. Here we prove that
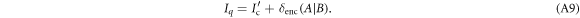
In order to explicitly evaluate  , we apply equation (A6), which can equivalently be written as
, we apply equation (A6), which can equivalently be written as
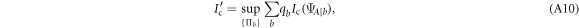
since any local rank-1 POVM  is optimal. Here, we have
is optimal. Here, we have
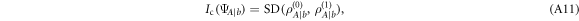
where
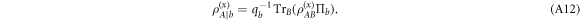
Since the two conditional codewords

and 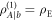 commute, we can resort to the Holevo information and write
commute, we can resort to the Holevo information and write

where
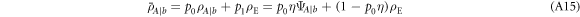
is the conditional output state averaged on the presence or not of the target. By using equation (A14) into equation (A10), we get
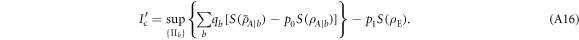
Now it is important to note that, in the previous equation, the von Neumann entropies 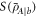 and
and  do not depend on the pure state
do not depend on the pure state 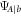 . In fact, for any pure
. In fact, for any pure  , we can expand the environmental state
, we can expand the environmental state  as
as
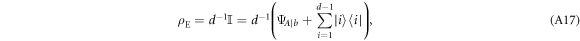
where 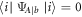 for any i. By replacing this expansion in equation (A15), we find the spectral decomposition
for any i. By replacing this expansion in equation (A15), we find the spectral decomposition
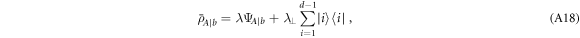
with probabilities
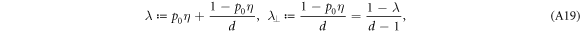
where 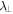 is
is  degenerate. The von Neumann entropy
degenerate. The von Neumann entropy  is equal to the Shannon entropy associated with the previous probability distribution, i.e.,
is equal to the Shannon entropy associated with the previous probability distribution, i.e.,

It is clear that the spectral decomposition of equation (A18) is exactly the same whatever the pure state  is. Thus, its entropy
is. Thus, its entropy  is independent from the specific pure state
is independent from the specific pure state 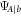 selected by the measurement operator of the rank-1 POVM. The reasoning can be repeated for the other state
selected by the measurement operator of the rank-1 POVM. The reasoning can be repeated for the other state 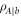 , which has the same spectral decomposition of
, which has the same spectral decomposition of 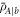 proviso that we set
proviso that we set 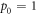 in equation (A19).
in equation (A19).
Therefore we have that 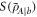 and
and 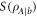 , and also their difference
, and also their difference 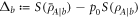 , do not depend on the pure state
, do not depend on the pure state 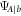 : these quantities are the same for any choice of the measurement operator
: these quantities are the same for any choice of the measurement operator 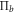 of any rank-1 POVM
of any rank-1 POVM 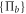 . As a result of this measurement-independence, we can pick an arbitrary outcome
. As a result of this measurement-independence, we can pick an arbitrary outcome  of an arbitrarily chosen rank-1 POVM and write the following
of an arbitrarily chosen rank-1 POVM and write the following
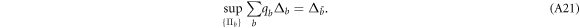
Because of the measurement-independence, we can also write
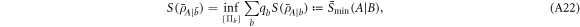

so that we find

By using equations (A21) and (A24) in equation (A16) we then write
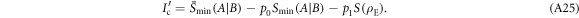
Now we are ready compute the difference  , which is given by
, which is given by

where
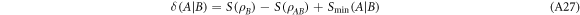
can be recognized to be the discord of 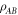 . Note that
. Note that ![${\rho }_{B}^{(x)}={\mathrm{Tr}}_{A}[{\rho }_{{AB}}^{(x)}]$](https://content.cld.iop.org/journals/1367-2630/18/4/043027/revision1/njpaa135eieqn203.gif) is equal to
is equal to 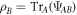 for any x, so that
for any x, so that

This means that we can use the equality 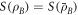 in equation (A26), which gives
in equation (A26), which gives
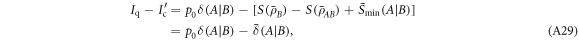
where 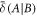 is the discord of the average state
is the discord of the average state 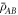 . Thus, we finally get
. Thus, we finally get 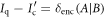 proving our statement (ii). Combining this with statement (i) proves the main result of our manuscript, i.e.,
proving our statement (ii). Combining this with statement (i) proves the main result of our manuscript, i.e., 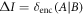 .
.