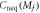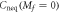Abstract
We identify a new class of phase transitions when calculating the Hall conductance of two-band Chern insulators in the long-time limit after a global quench of the Hamiltonian. The Hall conductance is expressed as the integral of the Berry curvature in the diagonal ensemble. Even if the Chern number of the unitarily-evolving wave function is conserved, the Hall conductance as a function of the energy gap in the post-quench Hamiltonian displays a continuous but nonanalytic behavior, that is it has a logarithmically divergent derivative as the gap closes. The coefficient of this logarithmic function is the ratio of the change of the Chern number for the ground state of the post-quench Hamiltonian to the energy gap in the initial state. This nonanalytic behavior is universal in two-band Chern insulators.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The discovery of the quantum Hall effect [1, 2], i.e. a quantized Hall conductance in the ground state which jumps from one plateau to another, inspired the study of characterizing different topological states of matter outside the conventional framework of spontaneous symmetry breaking [3, 4]. Considerable effort has been devoted to understanding topological phases in the ground state. More recently, a lot of attention was devoted to the properties of the topological states driven out of equilibrium, in particular for quantum quenches of the Hamiltonian [5–13].
Consider an isolated system initially in the ground state of a Hamiltonian  and suddenly changing the Hamiltonian to
and suddenly changing the Hamiltonian to 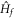 . The wave function follows a unitary time evolution, while the local observables in the long time limit settle to the prediction of the diagonal ensemble [14], which in some cases can be reduced to a thermal ensemble for nonintegrable systems or a generalized Gibbs ensemble [15, 16] for integrable systems. Topological order or topological invariant cannot be expressed as a local observable. Therefore, its identification in a nonequilibrium state is far from trivial. In the toric code model, the topological entropy which measures the long-range entanglement in the long time limit is found to be the same as its initial value independent from whether the ground states of
. The wave function follows a unitary time evolution, while the local observables in the long time limit settle to the prediction of the diagonal ensemble [14], which in some cases can be reduced to a thermal ensemble for nonintegrable systems or a generalized Gibbs ensemble [15, 16] for integrable systems. Topological order or topological invariant cannot be expressed as a local observable. Therefore, its identification in a nonequilibrium state is far from trivial. In the toric code model, the topological entropy which measures the long-range entanglement in the long time limit is found to be the same as its initial value independent from whether the ground states of 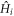 or
or  are topologically trivial or not [5–7]. This result agrees with a universal argument for gapped spin liquids [17], which states that local unitary transformations do not change the long-range entanglement. Similarly, for the Fermi gas on a honeycomb lattice which essentially simulates the Haldane model, the Chern number is proved to be conserved under unitary evolution [18, 19]. However, in the two-dimensional topological superfluid, the winding number of the retarded Green's function after a quench shows a strong dependence on the post-quench Hamiltonian
are topologically trivial or not [5–7]. This result agrees with a universal argument for gapped spin liquids [17], which states that local unitary transformations do not change the long-range entanglement. Similarly, for the Fermi gas on a honeycomb lattice which essentially simulates the Haldane model, the Chern number is proved to be conserved under unitary evolution [18, 19]. However, in the two-dimensional topological superfluid, the winding number of the retarded Green's function after a quench shows a strong dependence on the post-quench Hamiltonian  [8, 9], even if the winding of the Anderson pseudo spin texture is conserved [10]. Here the Chern number and the winding numbers are all topological invariants which equal each other in ground states. Also in the one-dimensional topological superfluid, an analysis of tunneling spectroscopy by coupling the system to an auxiliary thermal bath shows that the topological properties are mostly determined by
[8, 9], even if the winding of the Anderson pseudo spin texture is conserved [10]. Here the Chern number and the winding numbers are all topological invariants which equal each other in ground states. Also in the one-dimensional topological superfluid, an analysis of tunneling spectroscopy by coupling the system to an auxiliary thermal bath shows that the topological properties are mostly determined by  [11]. But in topological superconductors with proximity-induced superconductivity, the Majorana order parameter [12] or the entanglement spectrum [13] indicate that the quenched state is topologically trivial if
[11]. But in topological superconductors with proximity-induced superconductivity, the Majorana order parameter [12] or the entanglement spectrum [13] indicate that the quenched state is topologically trivial if 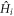 and
and 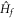 are in different topological phases.
are in different topological phases.
To clarify the issue of topological order far from equilibrium, we appeal to a measurable physical quantity, namely the Hall conductance in Chern insulators. We first study a paradigmatic model, i.e. the Dirac model [20], and then extend our results to a general two-band Chern insulator. We find that the Chern number of the unitarily-evolving wave function is conserved and uniquely determined by 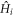 . However, while the Hall conductance of the quenched state is a continuous function of the energy gap in
. However, while the Hall conductance of the quenched state is a continuous function of the energy gap in  , the derivative of this function displays a logarithmic divergence whenever the Chern number for the ground state of the post-quench Hamiltonian changes. We thus identify a new class of phase transitions with an exotic critical behavior, which is quite different from the orthodox one in which the Hall conductance is discontinuous but its derivative is zero everywhere in the phase diagram. The discrepancy between the Chern number based on unitary time evolution and the Hall conductance is attributed to the fact that the latter must be calculated from the diagonal ensemble, in which the coherence between different eigenstates of
, the derivative of this function displays a logarithmic divergence whenever the Chern number for the ground state of the post-quench Hamiltonian changes. We thus identify a new class of phase transitions with an exotic critical behavior, which is quite different from the orthodox one in which the Hall conductance is discontinuous but its derivative is zero everywhere in the phase diagram. The discrepancy between the Chern number based on unitary time evolution and the Hall conductance is attributed to the fact that the latter must be calculated from the diagonal ensemble, in which the coherence between different eigenstates of 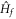 in the wave function is lost in the long-time limit.
in the wave function is lost in the long-time limit.
The contents of the paper are arranged as follows. In section 2, we discuss the Chern number of the unitarily-evolving wave function. We derive the formula for the Hall conductance of the diagonal ensemble in section 3. In section 4, we first discuss the nonanalytic behavior of the Hall conductance in the Dirac model and then extend our results to general two-band Chern insulators. At last, a concluding section summarizes our results.
2. Real-time dynamics of the Chern number
The Hamiltonian of a two-band Chern insulator in two-dimensions is expressed as
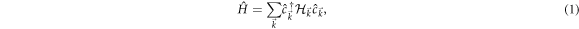
where 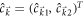 is the fermionic operator and
is the fermionic operator and 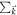 sums over a single Brillouin zone. The single-particle Hamiltonian
sums over a single Brillouin zone. The single-particle Hamiltonian 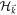 can be decomposed into
can be decomposed into 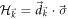 , where
, where 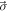 denotes the Pauli matrices, reading
denotes the Pauli matrices, reading

The Dirac model is a paradigm for two-band Chern insulators [20]. In the Dirac model, the coefficients of the Pauli matrices are 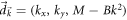 with two parameters M and B, and
with two parameters M and B, and 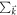 sums over the whole momentum plane. The ground state is well known to be classified by the Chern number
sums over the whole momentum plane. The ground state is well known to be classified by the Chern number 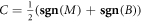 , which is quantized and changes only at the phase boundary M = 0 or B = 0. The Hall conductance of the ground state is simply the Chern number in units of
, which is quantized and changes only at the phase boundary M = 0 or B = 0. The Hall conductance of the ground state is simply the Chern number in units of 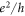 .
.
At the time t = 0, we suddenly change the Hamiltonian from 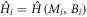 to
to 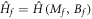 . Then the wave function evolves according to
. Then the wave function evolves according to 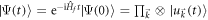 , where
, where 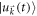 is the single-particle wave function obeying
is the single-particle wave function obeying 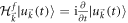 . The momentum is a good quantum number both in
. The momentum is a good quantum number both in 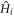 and
and 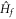 . Therefore, it is natural to generalize the definition of the Chern number for the time-dependent wave function in the following way:
. Therefore, it is natural to generalize the definition of the Chern number for the time-dependent wave function in the following way:
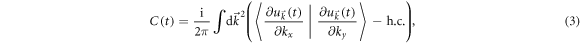
where the integral is over the whole momentum plane. This real-time Chern number characterizes the topological property of the wave function 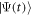 , and can be re-expressed as
, and can be re-expressed as 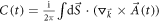 , where
, where 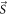 denotes the kx-ky plane oriented in the kz-direction and
denotes the kx-ky plane oriented in the kz-direction and 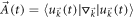 is the Berry connection with its curl in the kz-direction being
is the Berry connection with its curl in the kz-direction being 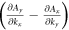 . C(t) is determined by the poles of
. C(t) is determined by the poles of  and must remain quantized at all times since locally deforming
and must remain quantized at all times since locally deforming 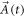 cannot change it. In fact, the two poles of
cannot change it. In fact, the two poles of  at k = 0 and
at k = 0 and 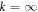 have conserved residues under a unitary evolution (see appendix
have conserved residues under a unitary evolution (see appendix  and
and 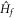 we have
we have  . The Chern number of the wave function never changes although the system is driven out of equilibrium, which agrees with the previous results in different models [18, 19].
. The Chern number of the wave function never changes although the system is driven out of equilibrium, which agrees with the previous results in different models [18, 19].
3. Hall conductance in the diagonal ensemble
The observation that C(t) is independent of 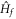 does not imply the absence of nonequilibrium phase transitions because C(t) is not a measurable physical quantity. In this paper, a nonequilibrium phase transition is unambiguously indicated by the nonanalytic behavior of observables as the post-quench Hamiltonian
does not imply the absence of nonequilibrium phase transitions because C(t) is not a measurable physical quantity. In this paper, a nonequilibrium phase transition is unambiguously indicated by the nonanalytic behavior of observables as the post-quench Hamiltonian  changes. We choose the Hall conductance as the indicator of nonequilibrium phase transitions. Notice that in the ground state the Hall conductance is directly related to the Chern number.
changes. We choose the Hall conductance as the indicator of nonequilibrium phase transitions. Notice that in the ground state the Hall conductance is directly related to the Chern number.
It is well known that the Hall conductance cannot be expressed as the expectation value of a local operator, but must be written as the long-time response to an external electric field in linear response theory. And an important observation is that in the long-time limit the far-from-equilibrium system can be described by the diagonal ensemble. This motivates us to study the Hall conductance in the diagonal ensemble, which is the experimentally relevant setting. In the long-time limit, the off-diagonal terms of the density matrix in the eigenbasis of 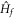 are averaged out [14]. The time-averaged expectation value of an operator
are averaged out [14]. The time-averaged expectation value of an operator  can be expressed as
can be expressed as
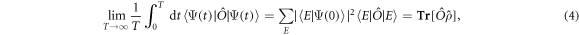
where 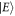 are the eigenstates of
are the eigenstates of 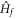 and
and 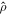 is diagonal in the basis
is diagonal in the basis 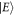 with the elements
with the elements 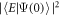 . If the long-time limit of
. If the long-time limit of 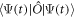 exists, it must be determined by
exists, it must be determined by 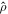 , the so-called diagonal ensemble [14]. While this argument is based on nondegenerate eigenenergies, the applicability of the diagonal ensemble has also been shown in many integrable quantum many-body models [21, 22].
, the so-called diagonal ensemble [14]. While this argument is based on nondegenerate eigenenergies, the applicability of the diagonal ensemble has also been shown in many integrable quantum many-body models [21, 22].
We build our formalism on the diagonal ensemble with the density matrix written as
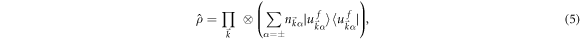
where 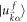 is the eigenvector of
is the eigenvector of 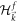 and
and  denotes the upper and lower bands with the positive and negative eigenvalues
denotes the upper and lower bands with the positive and negative eigenvalues 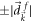 , respectively.
, respectively. 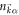 is the occupation number of the band α and can be expressed as the overlap
is the occupation number of the band α and can be expressed as the overlap 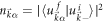 , where
, where 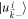 is the lower-band eigenvector of the initial Hamiltonian
is the lower-band eigenvector of the initial Hamiltonian 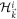 , which is in fact the initial wave function. The total occupation at each
, which is in fact the initial wave function. The total occupation at each 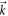 is conserved to be
is conserved to be 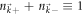 . Equation (5) is obtained by averaging out the off-diagonal elements in
. Equation (5) is obtained by averaging out the off-diagonal elements in 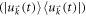 .
.
Now we calculate the Hall conductance of the diagonal ensemble in linear response theory [23], i.e., we replace the equilibrium density matrix in linear response theory by the diagonal ensemble  . This replacement does not cause any problem in the formalism because
. This replacement does not cause any problem in the formalism because 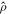 is time-independent satisfying
is time-independent satisfying ![$[\hat{\rho },{\hat{H}}_{f}]=0$](https://content.cld.iop.org/journals/1367-2630/18/5/053003/revision1/njpaa2011ieqn64.gif) . We can then express the Hall conductance as the current–current correlation in the diagonal ensemble:
. We can then express the Hall conductance as the current–current correlation in the diagonal ensemble:
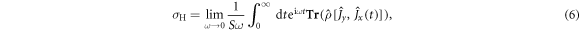
where S denotes the area of the system and is conventionally set to unity. 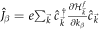 is the current operator along the β-direction with e denoting the charge of the particle. Following the process for obtaining the celebrated TKNN number [3], we re-express the dimensionless Hall conductance
is the current operator along the β-direction with e denoting the charge of the particle. Following the process for obtaining the celebrated TKNN number [3], we re-express the dimensionless Hall conductance 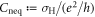 as (see appendix
as (see appendix
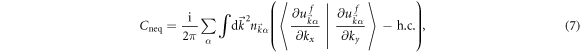
which is the integral of the weighted mixture of Berry curvatures in different bands of the post-quench Hamiltonian. We note that a similar formula has been obtained by studying the unitary evolution of a closed system in Floquet states under an infinitesimal external electric field [24, 25]. In the case of  (no quench), the occupation is
(no quench), the occupation is 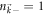 and
and 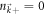 everywhere in the Brillouin zone, and Cneq is just the Chern number of the initial state as we expect. But for
everywhere in the Brillouin zone, and Cneq is just the Chern number of the initial state as we expect. But for  ,
, ![${n}_{\vec{k}\alpha }\in [0,1]$](https://content.cld.iop.org/journals/1367-2630/18/5/053003/revision1/njpaa2011ieqn71.gif) becomes a continuous function of
becomes a continuous function of 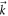 so that Cneq is not quantized any more but can take an arbitrary value.
so that Cneq is not quantized any more but can take an arbitrary value.
It is worth comparing the real time Chern number C(t) in equation (3) with the dimensionless Hall conductance Cneq in equation (7). The former reflects the topology of the wave function, being quantized but not measurable, while the latter is a true observable but not quantized. They are both integrals of the Berry curvature, but C(t) is derived from the wave function while Cneq follows from the diagonal ensemble where the coherence is lost.
4. Nonanalytic behavior of Hall conductance
In the Dirac model, it is straightforward to determine the Hall conductance as (see appendix
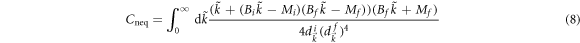
with 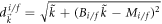 . The Hall conductance Cneq is a function of
. The Hall conductance Cneq is a function of 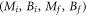 , i.e., the parameters of
, i.e., the parameters of 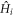 and
and 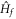 . This function satisfies the properties:
. This function satisfies the properties:
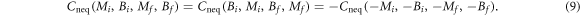
Let us study this function as 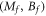 changes, while
changes, while 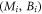 is invariant, i.e., the initial state is fixed. Due to equation (9), we only consider the cases
is invariant, i.e., the initial state is fixed. Due to equation (9), we only consider the cases 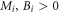 and
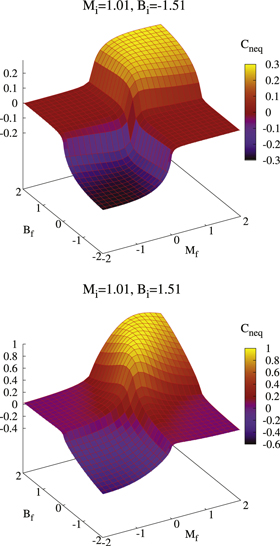
and 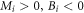 . As shown in figure 1, Cneq is a continuous function of
. As shown in figure 1, Cneq is a continuous function of  in the whole parameter space (we strictly prove this in appendix
in the whole parameter space (we strictly prove this in appendix 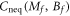 is insensitive to
is insensitive to 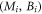 . As
. As 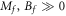 (
(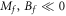 ), Cneq takes a positive (negative) value, while Cneq is close to zero as Mf and Bf have different signs. Even if the initial state is topologically trivial (see figure 1, the top panel), the Hall conductance is finite as
), Cneq takes a positive (negative) value, while Cneq is close to zero as Mf and Bf have different signs. Even if the initial state is topologically trivial (see figure 1, the top panel), the Hall conductance is finite as 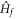 is in the nontrivial regime, but it cannot reach the quantized values
is in the nontrivial regime, but it cannot reach the quantized values 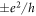 . When the initial state is nontrivial (see figure 1, the bottom panel), the Hall conductance is suppressed as
. When the initial state is nontrivial (see figure 1, the bottom panel), the Hall conductance is suppressed as 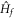 deviates from
deviates from  , and can even change the sign as Mf and Bf both change their signs.
, and can even change the sign as Mf and Bf both change their signs.
Figure 1. Hall conductance Cneq as a function of 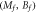 at different
at different  in the Dirac model. [Top panel] the initial state is topologically trivial. [Bottom panel] the initial state is topologically nontrivial.
in the Dirac model. [Top panel] the initial state is topologically trivial. [Bottom panel] the initial state is topologically nontrivial.
Download figure:
Standard image High-resolution imageWhile 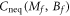 is continuous, the key finding is that whenever the post-quench Hamiltonian crosses the boundary at Mf = 0 (Bf = 0), the derivative of the Hall conductance
is continuous, the key finding is that whenever the post-quench Hamiltonian crosses the boundary at Mf = 0 (Bf = 0), the derivative of the Hall conductance 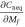 (
(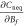 ) diverges to
) diverges to 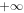 in a logarithmic way (see appendix
in a logarithmic way (see appendix
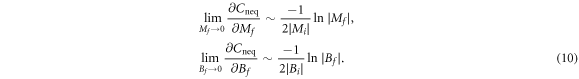
As 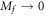 ,
, 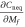 as a function of
as a function of 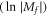 asymptotically approaches a straight line with the slope
asymptotically approaches a straight line with the slope 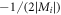 , which is independent of
, which is independent of 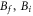 and the side from which Mf goes to zero. As
and the side from which Mf goes to zero. As  ,
, 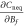 has a similar divergence since Cneq is invariant under the exchange of Mf and Bf according to equation (9). We identify a nonequilibrium phase transition when the Chern number for the ground state of
has a similar divergence since Cneq is invariant under the exchange of Mf and Bf according to equation (9). We identify a nonequilibrium phase transition when the Chern number for the ground state of 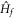 changes. The critical behavior of this phase transition is exotic, compared to that of ground-state phase transitions in which the Hall conductance has a zero derivative everywhere but displays a discontinuity at the phase boundary.
changes. The critical behavior of this phase transition is exotic, compared to that of ground-state phase transitions in which the Hall conductance has a zero derivative everywhere but displays a discontinuity at the phase boundary.
This phase transition reveals different nonequilibrium phases which share the common symmetries of the Dirac model. Therefore, the broken symmetry picture does not account for this transition. Interestingly, the topological invariant of the unitarily-evolving wave function C(t) is independent of  , and then fails to characterize different phases in this nonequilibrium phase transition. One can assign the Chern number for the ground-state wave function of
, and then fails to characterize different phases in this nonequilibrium phase transition. One can assign the Chern number for the ground-state wave function of 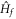 to each nonequilibrium phase to distinguish them.
to each nonequilibrium phase to distinguish them.
Now let us consider a general two-band Chern insulator in two-dimensions with the Hamiltonian given by equation (1). The coefficient vector  is different from model to model. But the nonanalytic behavior of Hall conductance is insensitive to the change of
is different from model to model. But the nonanalytic behavior of Hall conductance is insensitive to the change of 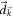 . Instead, it depends only upon the lowest-order expansion of
. Instead, it depends only upon the lowest-order expansion of 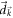 at the momentum
at the momentum 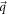 where the energy gap closes (
where the energy gap closes ( ) at a phase boundary. In a generic model, two components of
) at a phase boundary. In a generic model, two components of 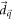 must be zero. Let us suppose them to be
must be zero. Let us suppose them to be 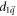 and
and 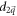 without loss of generality. The energy gap is
without loss of generality. The energy gap is 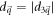 when the system is close to the phase boundary.
when the system is close to the phase boundary. 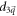 is a free parameter in the Hamiltonian (the gap parameter), which is denoted by m. Note that m = M in the Dirac model.
is a free parameter in the Hamiltonian (the gap parameter), which is denoted by m. Note that m = M in the Dirac model.
Suppose that the system is initially in a ground state with the gap parameter 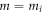 , before we suddenly change m in the Hamiltonian from mi to mf. We measure the Hall conductance in the long time limit. The Hall conductance Cneq is a function of mf, while we fix mi to be nonzero. The function
, before we suddenly change m in the Hamiltonian from mi to mf. We measure the Hall conductance in the long time limit. The Hall conductance Cneq is a function of mf, while we fix mi to be nonzero. The function 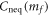 is continuous but nonanalytic at mf = 0, where the gap of the post-quench Hamiltonian
is continuous but nonanalytic at mf = 0, where the gap of the post-quench Hamiltonian 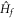 closes. The derivative of
closes. The derivative of 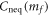 satisfies (see appendix
satisfies (see appendix

where 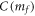 denotes the Chern number in the ground-state wave function of
denotes the Chern number in the ground-state wave function of 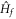 . The derivative of the Hall conductance with respect to the energy gap in
. The derivative of the Hall conductance with respect to the energy gap in 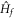 is logarithmically divergent as the gap closes. And the coefficient of this logarithmic function is the ratio of the change of Chern number for the ground state of
is logarithmically divergent as the gap closes. And the coefficient of this logarithmic function is the ratio of the change of Chern number for the ground state of 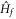 to the energy gap in the initial state. Equation (11) relates the nonequilibrium phase transition in quenched states to the topological phase transition in ground states. Equation (10) for the Dirac model is a special case of equation (11) as the change of Chern number is −1.
to the energy gap in the initial state. Equation (11) relates the nonequilibrium phase transition in quenched states to the topological phase transition in ground states. Equation (10) for the Dirac model is a special case of equation (11) as the change of Chern number is −1.
5. Conclusions
In summary, we find a new class of phase transitions in quenched states of two-band Chern insulators, which are characterized by the Hall conductance as a continuous function of the energy gap in the post-quench Hamiltonian 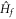 with a logarithmically divergent derivative. The asymptotic behavior of the Hall conductance is determined by the ratio of the change of the Chern number for the ground state of
with a logarithmically divergent derivative. The asymptotic behavior of the Hall conductance is determined by the ratio of the change of the Chern number for the ground state of 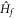 to the energy gap in the initial state, which is universal in two-band Chern insulators. We obtain the Hall conductance by applying linear response theory to the diagonal ensemble of the system, which is the physically correct description of the long-time limit in a far-from-equilibrium quench setup. The topological invariant of the real-time wave function fails to predict this phase transition, which can only be correctly identified in the diagonal ensemble where decoherence effects are taken into account. Our finding indicates the possibility of exotic topological phase transitions in systems far from equilibrium.
to the energy gap in the initial state, which is universal in two-band Chern insulators. We obtain the Hall conductance by applying linear response theory to the diagonal ensemble of the system, which is the physically correct description of the long-time limit in a far-from-equilibrium quench setup. The topological invariant of the real-time wave function fails to predict this phase transition, which can only be correctly identified in the diagonal ensemble where decoherence effects are taken into account. Our finding indicates the possibility of exotic topological phase transitions in systems far from equilibrium.
Finally, we discuss the conditions for observing this phase transition in experiments. The nonequilibrium distribution of particles is responsible for the logarithmically divergent derivative of the Hall conductance. Ultracold atomic gases are known to be well isolated from the environment and suitable for studying the quench dynamics of many-body quantum systems [26]. The Haldane model [27] was recently realized with cold atoms in an optical lattice [28]. The Haldane model is a two-band Chern insulator, in which the quenched-state Hall conductance displays the nonanalytic behavior in equation (11). The direct measurement of the Hall conductance in cold atoms is difficult. But the Hall conductance can be obtained from the Faraday rotation angle [29]. Therefore, we expect our prediction to be verified by measuring the Faraday rotation angle of the cold atoms on an optical lattice that simulates the Haldane model.
Acknowledgments
We thank Professor Q Niu for inspiring discussions. We thank J Oberreuter and M Medvedyeva for their help in preparing the paper. Pei Wang is supported by NSFC under Grant No. 11304280, and by China Scholarship Council. SK was supported through SFB 1073 (project B03) of the Deutsche Forschungsgemeinschaft (DFG).
Appendix A.: The real-time Chern number C(t) in the Dirac model
We express the real-time Chern number as
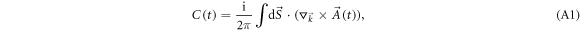
where 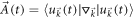 is the Berry connection with
is the Berry connection with 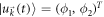 denoting the single-particle wave function. In the Dirac model, it is straightforward to calculate the wave function and obtain
denoting the single-particle wave function. In the Dirac model, it is straightforward to calculate the wave function and obtain
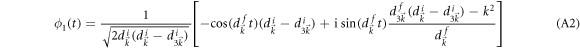
and
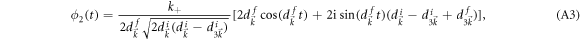
where 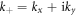 ,
,  is the coefficient vector in the initial and post-quench Hamiltonians, respectively, and
is the coefficient vector in the initial and post-quench Hamiltonians, respectively, and 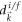 is the length of
is the length of 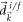 . We divide the Berry connection into
. We divide the Berry connection into 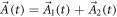 with
with 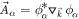 . Noticing that
. Noticing that 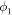 is a function of
is a function of 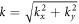 , we immediately know that
, we immediately know that 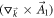 must be zero, so that
must be zero, so that 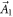 does not contribute to C(t). We again divide
does not contribute to C(t). We again divide 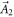 into the irrelevant term
into the irrelevant term  with a zero curl and the relevant term
with a zero curl and the relevant term 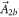 with its imaginary part written as
with its imaginary part written as
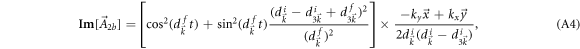
where 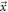 and
and 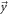 denote the unit vectors in the momentum plane.
denote the unit vectors in the momentum plane.
Now we re-express the Chern number by the vector field ![${\bf{Im}}[{\vec{A}}_{2b}]$](https://content.cld.iop.org/journals/1367-2630/18/5/053003/revision1/njpaa2011ieqn143.gif) as
as
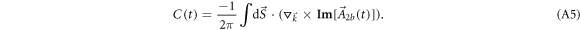
![${\bf{Im}}[{\vec{A}}_{2b}]$](https://content.cld.iop.org/journals/1367-2630/18/5/053003/revision1/njpaa2011ieqn144.gif) is a vortex field with two poles at zero and infinity, respectively. Applying the Kelvin–Stokes theorem in an annulus with inner radius r and outer radius R, and then taking the limit
is a vortex field with two poles at zero and infinity, respectively. Applying the Kelvin–Stokes theorem in an annulus with inner radius r and outer radius R, and then taking the limit  and
and 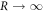 , we obtain
, we obtain
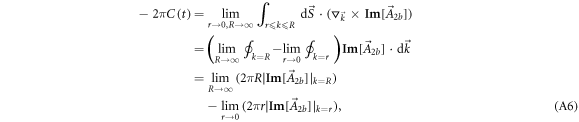
where ![$| {\bf{Im}}[{\vec{A}}_{2b}]{| }_{k=R}$](https://content.cld.iop.org/journals/1367-2630/18/5/053003/revision1/njpaa2011ieqn147.gif) denotes the length of the vector
denotes the length of the vector ![${\bf{Im}}[{\vec{A}}_{2b}]$](https://content.cld.iop.org/journals/1367-2630/18/5/053003/revision1/njpaa2011ieqn148.gif) at the circle of radius
at the circle of radius 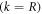 . The first limit evaluates
. The first limit evaluates 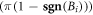 , while the second limit evaluates
, while the second limit evaluates 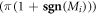 , being both time-independent. In other words, the residues of
, being both time-independent. In other words, the residues of ![${\bf{Im}}[{\vec{A}}_{2b}]$](https://content.cld.iop.org/journals/1367-2630/18/5/053003/revision1/njpaa2011ieqn152.gif) at zero and infinity are both time-invariant, which leads to a conserved Chern number:
at zero and infinity are both time-invariant, which leads to a conserved Chern number:
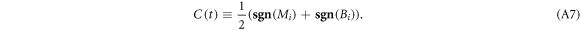
Appendix B.: The Hall conductance of quenched states
In this section, we first show how to express the Hall conductance of quenched states as the integral of the Berry curvature. Our derivation is a straightforward extension of the work by Thouless et al [3]. We then express the Hall conductance by using the coefficient vectors in two-band Chern insulators.
In linear response theory, the Hall conductance is written as

where η is an infinitesimal number corresponding to the adiabatic switch-on of an external electric field, and ω is the frequency of the electric field with the limit  corresponding to the dc-conductance. The diagonal ensemble is known to be
corresponding to the dc-conductance. The diagonal ensemble is known to be  , which is a product state. Due to the conversation law
, which is a product state. Due to the conversation law 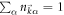 , the state of the system is limited in a subspace of the Fock space in which the empty or doubly-occupied states at each momentum are excluded. We can then re-express
, the state of the system is limited in a subspace of the Fock space in which the empty or doubly-occupied states at each momentum are excluded. We can then re-express 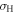 in the first-quantization language as
in the first-quantization language as
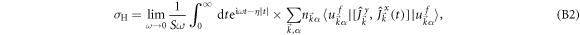
where the momentum-resolved current operator is 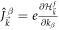 . Since we are interested in the dc Hall conductance which is a real number, we take the real part of
. Since we are interested in the dc Hall conductance which is a real number, we take the real part of 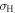 and obtain
and obtain
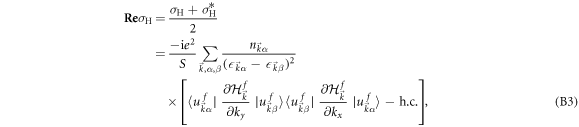
where 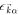 denotes the eigenvalue of
denotes the eigenvalue of 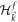 . We make use of the relation
. We make use of the relation 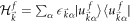 and finally obtain
and finally obtain
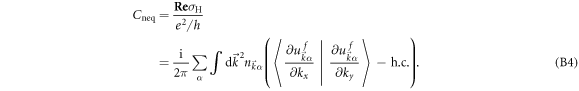
In a two-band Chern insulator with the Hamiltonian  , the Berry curvatures in different bands are opposite to each other. By using this and the conservation law
, the Berry curvatures in different bands are opposite to each other. By using this and the conservation law 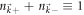 , we reexpress equation (B4) as
, we reexpress equation (B4) as
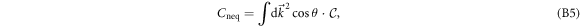
where  denotes the Berry curvature in the lower-band of the post-quench Hamiltonian
denotes the Berry curvature in the lower-band of the post-quench Hamiltonian  and can be expressed as
and can be expressed as
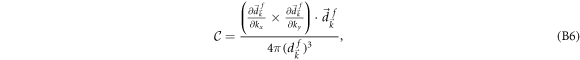
and  is the occupation factor defined as
is the occupation factor defined as
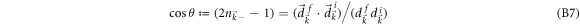
with θ denoting the angle between 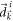 and
and 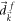 .
. 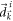 and
and 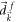 are the coefficients of the Pauli matrices in the initial and post-quench Hamiltonians, respectively, and
are the coefficients of the Pauli matrices in the initial and post-quench Hamiltonians, respectively, and 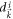 and
and 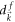 are the length of
are the length of 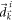 and
and 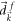 , respectively.
, respectively.
Appendix C.: Continuity and nonanalyticity of the Hall conductance in the Dirac model
In this section, we show how to prove the continuity of 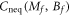 and the logarithmic divergence of its derivative at the phase boundary. We only prove the case at Mf = 0 when Bf is fixed to be nonzero, since
and the logarithmic divergence of its derivative at the phase boundary. We only prove the case at Mf = 0 when Bf is fixed to be nonzero, since 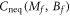 is invariant under the exchange of Mf and Bf.
is invariant under the exchange of Mf and Bf.
In the Dirac model, both 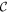 and
and 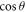 are rotationally invariant in the kx–ky plane. We can then carry out the azimuthal integration in equation (B5). By making a substitution
are rotationally invariant in the kx–ky plane. We can then carry out the azimuthal integration in equation (B5). By making a substitution 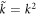 , we express the Hall conductance as
, we express the Hall conductance as
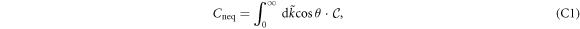
where the Berry curvature is
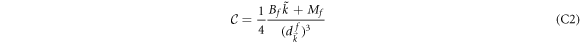
and the occupation factor is
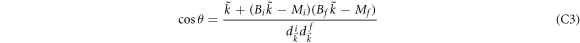
with 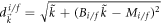 . At
. At 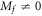 , we can express the derivative of Cneq as
, we can express the derivative of Cneq as

A straightforward observation is that both 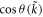 and
and  are smooth functions for
are smooth functions for 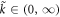 . However, they do not uniformly converge to
. However, they do not uniformly converge to 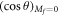 or
or 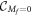 as
as 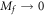 . The unique singularity is
. The unique singularity is 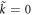 , at which we have
, at which we have 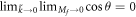 but
but 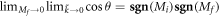 . And
. And 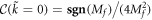 is divergent as
is divergent as 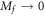 . We divide the integral into two parts:
. We divide the integral into two parts: 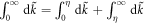 with
with 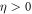 a number that can be arbitrarily small. The second integral is a smooth function of Mf, which can be proved by studying the asymptotic behavior of
a number that can be arbitrarily small. The second integral is a smooth function of Mf, which can be proved by studying the asymptotic behavior of 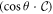 in the limit
in the limit 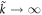 , or more precisely, by making a substitution
, or more precisely, by making a substitution 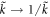 in the integral. In fact,
in the integral. In fact, 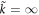 is a true singularity at the boundary Bf = 0, where
is a true singularity at the boundary Bf = 0, where 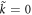 is a regular point, since
is a regular point, since 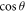 and
and 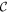 are invariant under the substitution
are invariant under the substitution 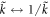 and
and 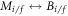 . If there is any nonanalytic behavior in the function
. If there is any nonanalytic behavior in the function 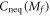 , it must come from the first integral denoted by
, it must come from the first integral denoted by  next. Interestingly, we can choose an arbitrarily small η so that
next. Interestingly, we can choose an arbitrarily small η so that 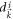 in
in 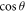 converges to a constant
converges to a constant 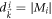 . We then obtain
. We then obtain

The calculation of this integral is straightforward since the integrand is rational.
We express the result as 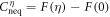 with F denoting the original function. The expression of F is lengthy, but it is an elementary function.
with F denoting the original function. The expression of F is lengthy, but it is an elementary function. 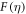 is a smooth function of Mf, while F(0) is expressed as
is a smooth function of Mf, while F(0) is expressed as
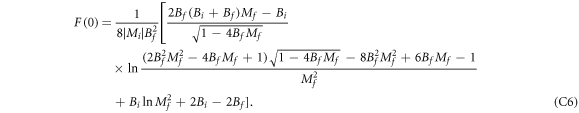
We are interested in F(0) as a function of Mf in the neighborhood of the phase boundary Mf = 0. We notice that 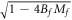 can be expanded at Mf = 0 into
can be expanded at Mf = 0 into
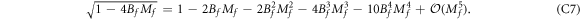
We substitute this expression into equation (C6) and obtain
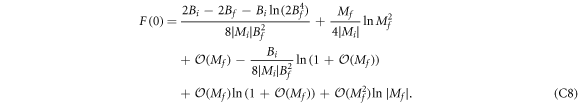
The first term is independent of Mf. The second term is a continuous function of Mf, but its derivative with respect to Mf is divergent as 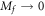 . All the other terms are continuous functions of Mf, and their derivatives with respect to Mf are finite at Mf = 0. The asymptotic behavior of
. All the other terms are continuous functions of Mf, and their derivatives with respect to Mf are finite at Mf = 0. The asymptotic behavior of 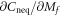 is uniquely determined by the second term. The function
is uniquely determined by the second term. The function 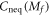 then asymptotically approaches
then asymptotically approaches  in the limit
in the limit 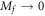 . This immediately leads to our results that
. This immediately leads to our results that 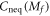 is continuous3
and
is continuous3
and 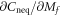 is logarithmically divergent as
is logarithmically divergent as
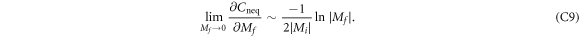
Furthermore, we calculate the Hall conductance by numerically integrate equation (B5). We plot 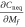 as a function of
as a function of 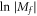 in figure 2. In the limit
in figure 2. In the limit 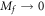 , the curves asymptotically approach straight lines with the slope
, the curves asymptotically approach straight lines with the slope 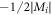 , which is independent of Bi, Bf and the side from which Mf goes to zero. The numerical result coincides well with our analysis.
, which is independent of Bi, Bf and the side from which Mf goes to zero. The numerical result coincides well with our analysis.
Figure 2.
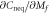 as a function of
as a function of 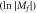 at different
at different 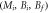 in the Dirac model. Note the curves at Mi = 1, in which we simultaneously plot the data at
in the Dirac model. Note the curves at Mi = 1, in which we simultaneously plot the data at 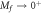 and at
and at 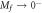 , which are in fact undistinguishable at small
, which are in fact undistinguishable at small  .
.
Download figure:
Standard image High-resolution imageAppendix D.: Universal nonanalytic behavior of the Hall conductance function in two-band Chern insulators
Let us consider a general two-band Chern insulator in two-dimensions with the Hamiltonian expressed as
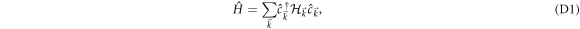
where the single-particle Hamiltonian can be decomposed into 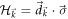 with
with 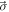 denoting the Pauli matrices. Examples include the Dirac model, the Haldane model [27] or the Kitaev honeycomb model in the fermionic basis [30, 31]. The coefficient vector
denoting the Pauli matrices. Examples include the Dirac model, the Haldane model [27] or the Kitaev honeycomb model in the fermionic basis [30, 31]. The coefficient vector 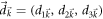 is different from model to model. But the nonanalytic behavior of Hall conductance is insensitive to the change of
is different from model to model. But the nonanalytic behavior of Hall conductance is insensitive to the change of 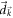 , but depends only upon the lowest-order expansion of
, but depends only upon the lowest-order expansion of  at the singularities of the Berry curvature.
at the singularities of the Berry curvature.
Let us first show how the Chern number of the ground-state wave function is related to the expansion of 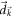 . The Chern number is expressed by the Berry connection as
. The Chern number is expressed by the Berry connection as

with
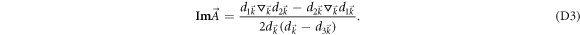
The Chern number must be zero when 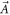 has no singularity in the Brillouin zone. According to Kelvin–Stokes theorem, the Chern number can be expressed as the line integral of
has no singularity in the Brillouin zone. According to Kelvin–Stokes theorem, the Chern number can be expressed as the line integral of 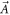 over the boundaries of the infinitesimal neighborhoods of singularities. Suppose that
over the boundaries of the infinitesimal neighborhoods of singularities. Suppose that 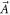 has a set of singularities
has a set of singularities 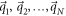 in a single Brillouin zone. The Chern number can be expressed as
in a single Brillouin zone. The Chern number can be expressed as
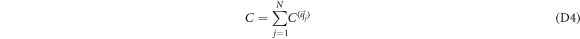
with
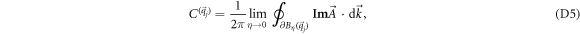
where 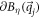 denotes the boundary of a circle of radius
denotes the boundary of a circle of radius 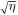 centered at
centered at 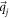 , and the integral is along the anticlockwise direction. Here we do not consider the singularity at infinity, since the Brillouin zone is finite in a generic model.
, and the integral is along the anticlockwise direction. Here we do not consider the singularity at infinity, since the Brillouin zone is finite in a generic model.
In general, a singularity of 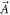 is a point
is a point 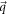 at which
at which 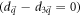 and then
and then 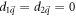 . In a generic model,
. In a generic model, 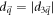 is the energy gap when the system is close to the phase boundary.
is the energy gap when the system is close to the phase boundary. 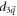 is a free parameter in the Hamiltonian, which is denoted by m next. Note that m = M in the Dirac model. m is zero if and only if the energy gap closes accompanied by a change of the Chern number.
is a free parameter in the Hamiltonian, which is denoted by m next. Note that m = M in the Dirac model. m is zero if and only if the energy gap closes accompanied by a change of the Chern number.
The Berry connection can be reexpressed as
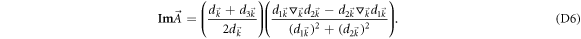
Since 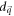 and
and 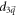 are finite at
are finite at 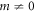 , we can replace
, we can replace 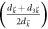 by its value at
by its value at 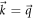 , which is
, which is 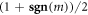 with
with 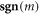 denoting the sign of m. This replacement will not change the integral in equation (D5) in the limit
denoting the sign of m. This replacement will not change the integral in equation (D5) in the limit  . The value of
. The value of 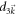 at
at 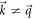 has nothing to do with the Chern number.
has nothing to do with the Chern number.
From equation (D5), we know that the Chern number depends only upon 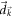 around the singularities of
around the singularities of 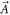 . We then expand
. We then expand  and
and 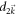 into power series of
into power series of  . Without loss of generality, we have
. Without loss of generality, we have

It is straight forward to prove that the higher-order terms in this expansion do not contribute to the integral in equation (D5) in the limit 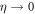 , which evaluates
, which evaluates
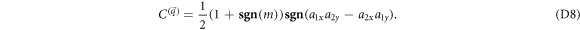
It is worth mentioning that the three components of 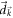 are on an equal footing. Depending on the basis that is chosen, the components of
are on an equal footing. Depending on the basis that is chosen, the components of 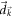 could be exchanged in some models.
could be exchanged in some models.
Notice that, in equation (D7), the coefficients a1x, a1y, a2x and a2y are 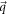 -dependent. While m at different
-dependent. While m at different 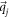 may represent different parameters in the Hamiltonian, i.e. the gap parameters at different phase boundaries. An example is the Haldane model [27]. In a single Brillouin zone,
may represent different parameters in the Hamiltonian, i.e. the gap parameters at different phase boundaries. An example is the Haldane model [27]. In a single Brillouin zone,  has two singularities. And the energy gap closes at one of them as the system is at some phase boundary, but closes at the other singularity as the system is at the different phase boundary. On the other hand, if the system has some symmetries so that at a specific phase boundary the gap closes simultaneously at several
has two singularities. And the energy gap closes at one of them as the system is at some phase boundary, but closes at the other singularity as the system is at the different phase boundary. On the other hand, if the system has some symmetries so that at a specific phase boundary the gap closes simultaneously at several  , m at these
, m at these 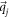 must be the same parameter.
must be the same parameter.
Now let us discuss the Hall conductance of quenched states when the parameters in the initial and post-quench Hamiltonians are both nearby a specific phase boundary where the gap parameter is denoted by m. Suppose that the system is initially in a ground state with the gap parameter  , before we suddenly change m in the Hamiltonian from mi to mf. We then measure the Hall conductance in the long time limit. The Hall conductance Cneq is a function of mf, while we fix mi to be nonzero.
, before we suddenly change m in the Hamiltonian from mi to mf. We then measure the Hall conductance in the long time limit. The Hall conductance Cneq is a function of mf, while we fix mi to be nonzero.
Noting 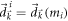 and
and  , we express the Hall conductance as
, we express the Hall conductance as
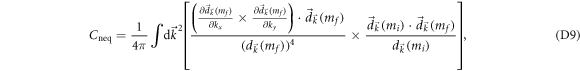
where the integral is over a single Brillouin zone. In a generic model, the components of 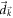 are all analytic functions of
are all analytic functions of 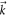 . According to equation (D9),
. According to equation (D9), 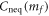 is nonanalytic only if
is nonanalytic only if 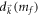 in the denominator of the integral vanishes at some
in the denominator of the integral vanishes at some 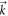 , i.e., the singularities of the Berry curvature. This is the case at mf = 0 when the gap of the post-quench Hamiltonian closes at some singularities of the Berry connection
, i.e., the singularities of the Berry curvature. This is the case at mf = 0 when the gap of the post-quench Hamiltonian closes at some singularities of the Berry connection 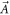 . Without loss of generality, we suppose that these singularities are
. Without loss of generality, we suppose that these singularities are  with
with  . The nonanalyticity of
. The nonanalyticity of 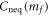 comes from the integral over the neighborhoods of
comes from the integral over the neighborhoods of 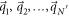 . We then divide Cneq into the analytic part and the nonanalytic part as we did in the Dirac model. The latter is written as
. We then divide Cneq into the analytic part and the nonanalytic part as we did in the Dirac model. The latter is written as
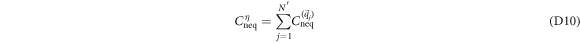
with

where  is a circle of radius
is a circle of radius  centered at
centered at 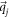 with η a positive number that can be arbitrarily small.
with η a positive number that can be arbitrarily small.
In the neighborhood of the singularity 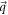 , we can expand the components of
, we can expand the components of 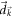 into power series. Let us first consider the lowest-order term given by equation (D7). We substitute equation (D7) into (D11). We replace
into power series. Let us first consider the lowest-order term given by equation (D7). We substitute equation (D7) into (D11). We replace 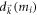 by its value at
by its value at 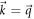 , that is
, that is 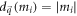 . This replacement will not change the nonanalytic behavior of
. This replacement will not change the nonanalytic behavior of 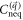 since mi is nonzero. While the denominator of the integrand becomes
since mi is nonzero. While the denominator of the integrand becomes
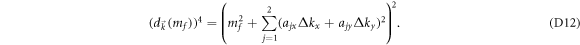
We change the coordinate system so that the function  has rotational symmetry around
has rotational symmetry around  . In the new coordinate system we have
. In the new coordinate system we have
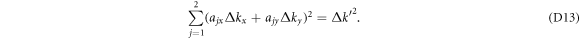
This transformation is always possible. Otherwise, the coefficients before 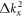 and
and 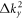 have different signs, which contradicts the proposition that
have different signs, which contradicts the proposition that 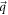 is an isolated singularity. In the new coordinate system, we carry out the azimuthal integration and obtain
is an isolated singularity. In the new coordinate system, we carry out the azimuthal integration and obtain
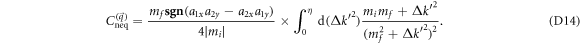
In the numerator of the integrand, only the 2nd-order term 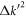 has a contribution to the nonanalyticity of
has a contribution to the nonanalyticity of 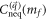 . It is trivial to find the original function of this integral, whose value is an analytic function of mf at
. It is trivial to find the original function of this integral, whose value is an analytic function of mf at 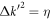 but a nonanalytic one at
but a nonanalytic one at 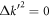 . This coincides with our expectation that the nonanalytic behavior of
. This coincides with our expectation that the nonanalytic behavior of 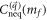 should be independent of the choice of η. The nonanalytic part of
should be independent of the choice of η. The nonanalytic part of 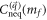 is
is

First, 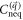 is a continuous function of mf, and then the Hall conductance
is a continuous function of mf, and then the Hall conductance 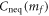 must be continuous. Second, the derivative of
must be continuous. Second, the derivative of 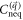 with respect to mf is logarithmically divergent in the limit
with respect to mf is logarithmically divergent in the limit 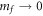 , i.e.,
, i.e.,
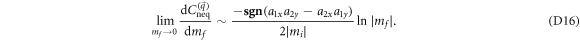
Comparing equation (D8) with (D16), we immediately find that the  -dependent coefficient in
-dependent coefficient in 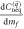 is equal to the change of
is equal to the change of 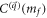 at the phase boundary mf = 0.
at the phase boundary mf = 0. 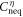 is the sum of
is the sum of 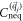 at the singularities
at the singularities 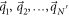 , while the Chern number C is the sum of
, while the Chern number C is the sum of 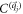 at all the singularities of
at all the singularities of 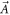 . But
. But 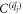 at
at 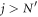 does not change at mf = 0, since the corresponding gap parameter is different from mf. We finally obtain
does not change at mf = 0, since the corresponding gap parameter is different from mf. We finally obtain
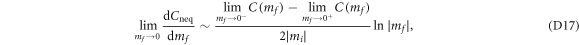
which is the central result of this paper.
Equation (D17) is obtained by considering only the lowest-order term in the expansion of 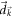 . Next we prove that the higher-order terms do not change the continuity of Cneq or the asymptotic behavior of
. Next we prove that the higher-order terms do not change the continuity of Cneq or the asymptotic behavior of  in the limit
in the limit 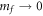 . This is true if the higher-order terms do not change the continuity of
. This is true if the higher-order terms do not change the continuity of  or the asymptotic behavior of
or the asymptotic behavior of  at an arbitrary singularity.
at an arbitrary singularity.
A linear term like 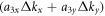 is not allowed in the expansion of
is not allowed in the expansion of 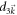 in equation (D7). Otherwise,
in equation (D7). Otherwise, 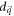 is not the energy gap, or the minimum point of
is not the energy gap, or the minimum point of 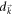 is not at
is not at 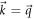 , but changes with m, which contradicts our proposition. In a generic model like the Dirac model, the Haldane model or the Kitaev honeycomb model, the minimum point of
, but changes with m, which contradicts our proposition. In a generic model like the Dirac model, the Haldane model or the Kitaev honeycomb model, the minimum point of 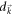 is determined by the symmetry of the model and then keeps invariant as the system is in the vicinity of the phase boundary.
is determined by the symmetry of the model and then keeps invariant as the system is in the vicinity of the phase boundary.
Let us add the 2nd-order term into 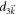 , i.e.,
, i.e., 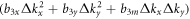 without loss of generality. The denominator in the integrand of
without loss of generality. The denominator in the integrand of 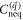 becomes
becomes
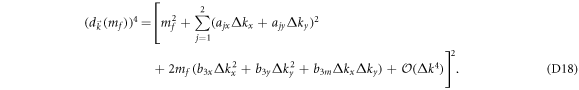
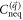 is an integral over the infinitesimal neighborhood of
is an integral over the infinitesimal neighborhood of 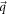 , where the 4th-order term
, where the 4th-order term  is much smaller than the 2nd-order term and can be neglected. At the same time, the additional 2nd-order term that is proportional to mf has no contribution to the asymptotic behavior of
is much smaller than the 2nd-order term and can be neglected. At the same time, the additional 2nd-order term that is proportional to mf has no contribution to the asymptotic behavior of 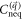 and
and 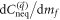 in the limit
in the limit  . Therefore, the effective denominator is the same as equation (D12). The numerator of the integrand becomes
. Therefore, the effective denominator is the same as equation (D12). The numerator of the integrand becomes
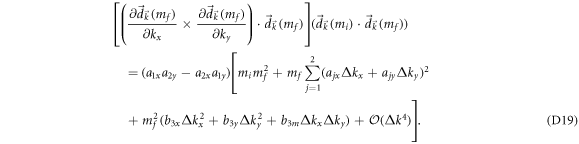
The 4th-order term 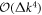 can be neglected in the limit
can be neglected in the limit 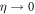 . This can be easily verified by adding
. This can be easily verified by adding 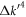 in the numerator of the integrand in equation (D14) and checking the output. The additional 2nd-order term that is proportional to mf2 leads to a correction of
in the numerator of the integrand in equation (D14) and checking the output. The additional 2nd-order term that is proportional to mf2 leads to a correction of 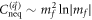 , which does not change the asymptotic behavior of
, which does not change the asymptotic behavior of 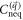 and
and 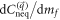 in the limit
in the limit 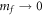 . In the power series of
. In the power series of 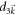 , any term in order higher than two leads to a correction to numerator or denominator of the integrand which is at least in the 3rd order of
, any term in order higher than two leads to a correction to numerator or denominator of the integrand which is at least in the 3rd order of 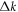 and can then be neglected in the limit
and can then be neglected in the limit 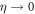 . Therefore, the higher-order terms in
. Therefore, the higher-order terms in 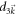 do not affect the asymptotic behavior of
do not affect the asymptotic behavior of 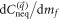 or the continuity of
or the continuity of  .
.
Similarly, we can prove that the higher-order terms in 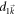 or
or 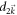 have no contribution. In fact, the terms in order higher than one lead to a correction of
have no contribution. In fact, the terms in order higher than one lead to a correction of 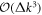 in the denominator. The terms in order higher than three also lead to a correction of
in the denominator. The terms in order higher than three also lead to a correction of 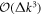 in the numerator, which can be neglected. The 2nd- and 3rd-order terms in
in the numerator, which can be neglected. The 2nd- and 3rd-order terms in 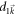 or
or 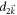 generate a linear term and a 2nd-order term that is proportional to mf2 in the numerator. The latter does not contribute to the asymptotic behavior of
generate a linear term and a 2nd-order term that is proportional to mf2 in the numerator. The latter does not contribute to the asymptotic behavior of 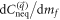 due to the similar reason mentioned above. While the linear term in the numerator is an odd function of
due to the similar reason mentioned above. While the linear term in the numerator is an odd function of 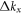 or
or 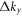 , and then has no contribution to the integral since both the denominator and the integration boundary have rotational symmetry with respect to the singularity.
, and then has no contribution to the integral since both the denominator and the integration boundary have rotational symmetry with respect to the singularity.
Footnotes
- 3
In this paper, '
 is continuous' means
is continuous' means  . Notice that these limits are not necessarily equal to
. Notice that these limits are not necessarily equal to  .
.