Abstract
Quantum spin models with spatially dependent interactions, known as compass models, play an important role in the study of frustrated quantum magnetism. One example is the Kitaev model on the honeycomb lattice with spin-liquid (SL) ground states and anyonic excitations. Another example is the geometrically frustrated quantum 120° model on the same lattice whose ground state has not been unambiguously established. To generalize the Kitaev model beyond the exactly solvable limit and connect it with other compass models, we propose a new model, dubbed 'the tripod model', which contains a continuum of compass-type models. It smoothly interpolates the Ising model, the Kitaev model, and the quantum 120° model by tuning a single parameter , the angle between the three legs of a tripod in the spin space. Hence it not only unifies three paradigmatic spin models, but also enables the study of their quantum phase transitions. We obtain the phase diagram of the tripod model numerically by tensor networks in the thermodynamic limit. We show that the ground state of the quantum 120° model has long-range dimer order. Moreover, we find an extended spin-disordered (SL) phase between the dimer phase and an antiferromagnetic phase. The unification and solution of a continuum of frustrated spin models as outline here may be useful to exploring new domains of other quantum spin or orbital models.
1. Introduction
Model Hamiltonians describing interacting spins localized on lattice sites are at the central stage in the field of quantum magnetism. A class of spin models, collectively known as the compass models [1], stand out owing to a unique feature they share in common: the spin exchange interactions differ for different lattice bond orientations. This is in contrast to the familiar Heisenberg model or the Ising model, where the exchange has the same form for all bonds connecting the nearest neighboring sites. The compass models arise naturally as low energy effective Hamiltonians in Mott insulators with orbital degrees of freedom [2–7] as well as interacting systems with spin–orbit coupling. These highly nontrivial models are also very appealing from a pure theoretical point of view because they offer a natural arena to study frustrated quantum magnetism [8, 9]. Exactly solvable compass models, the Kitaev model in particular, have played a pivotal role in stimulating the field of topological quantum computing [10, 11]. The rich physics contained in compass models has been reviewed recently in [1].
Our work is directly motivated by two well known compass models defined on the honeycomb lattice. The first example is the Kitaev model [11], where the exchange interactions between two neighboring sites are given by , and respectively. As shown by Kitaev, this model is exactly solvable and has anyonic excitations obeying fractional statistics [11]. The spatially dependent exchange interactions suppress long-range spin order and support a quantum spin liquid (SL) ground state, one of the most sought after exotic many-body states in condensed matter physics [12]. The Kitaev model, despite its theoretical appeal, is neither readily realized in materials nor easily simulated with synthetical quantum matter such as cold atoms on optical lattices. Recently, the hybrid Kitaev–Heisenberg model, a linear superposition of a Kitaev term and a Heisenberg term, was proposed for iridium oxides and solved numerically [13]. Besides the SL phase, the hybrid model contains other interesting phases such as the stripe and the zigzag phase due to the competition between the two terms [13]. The phase diagram becomes even richer when off-diagonal spin exchange interactions are added [14–16].
The second example of compass models is the quantum 120◦ model [6, 7]. It is very analogous to the Kitaev model but the spin operators , and for the three bond directions are replaced by three (pseudo)spin 1/2 operators , and T3 respectively. They form an angle of 120° with each other on the xz plane in spin space, hence the name 'the 120◦ model'. It was introduced to described the low energy physics of transition metal oxides [17] with doubly degenerate orbitals, e.g. orbital-only models of eg orbitals on cubic lattice [3]. Later, two of us, and Wu independently, found that the 120◦ model can be naturally realized in strongly interacting spinless p-orbital fermions on the honeycomb optical lattice [6, 7]. Although it is geometrically frustrated, spin wave analysis indicates that long-range order is stabilized by quantum fluctuations through the order by disorder mechanism [6, 7]. While the semiclassical spin-wave analysis is suggestive, the ground state of the 120◦ model on honeycomb lattice remains to be identified unambiguously.
Given the apparent similarities between the Kitaev model and the 120◦ model, it is natural to seek the conceptual and quantitative link between them. Indeed, these two models can be viewed as two instances of a more general class of compass models [18]. In this paper, we provide a concrete construction and propose a 'super model' which contains three paradigm models, the Ising, the Kitaev and the 120◦ model, as special limits. It only has a single tuning parameter and a simple, intuitive picture for the three (pseudo)spin operators: they form a tripod in spin space as shown in figure 1. Analogous to tuning the tripod to raise or low a mounted camera in photography, dialing the angle between the three legs takes the Ising model (tripod fully closed) smoothly to the Kitaev model (tripod open with three legs orthogonal to each other) and then to the 120◦ model (tripod fully open with three legs in the same plane). Immediately, one conjectures that the phase diagram of this continuum compass model is highly nontrivial containing drastically different long-range ordered states as well as SLs.
Figure 1. The tripod model on the honeycomb lattice, equation (1). (a) The nearest neighbor spin exchange along bond direction , is defined through the spin 1/2 operator , represented by an arrow in spin space spanned by . The three can be thought as the three legs of a tripod, being tilted out of the xz plane by angle θ, and forming an angle with each other. When projected onto the xz plane, is along the direction. (b) The schematic phase diagram of the tripod model. As the tripod is opened by increasing , the model starts as the Ising model at , becomes the Kitaev model at , and then the quantum 120° model at . Three phases are identified: a ordered antiferromagnet, a spin liquid (SL), and a long-range ordered dimer phase.
Download figure:
Standard image High-resolution imageWe obtain the phase diagram of this 'super model' using tensor network states which have gained considerable success recently in the study of frustrated magnetism [19–22]. The results are summarized in figures 1 and 2. The order parameters are calculated using the tensor renormalization group (TRG) method formulated in thermodynamic limit [23, 24]. We show that the ground state of the quantum 120◦ model is a long-range ordered dimer phase, and a SL phase exists in an extended region in our phase diagram5 . The numerical results of TRG are further confirmed and crosschecked with projected entangled pair states (PEPS) calculations [25, 26] for finite systems, exact diagonalization (ED), and spin wave analysis. We discuss the qualitative features of the quantum phase transitions between the SL phase and the dimer phase by introducing a topological charge (spin vortex) for the dimer configuration. We further show that the proposed tripod model can in principle be simulated with Hubbard model in the Mott insulating regime, e.g., using cold atoms on optical lattice with artificial gauge fields.
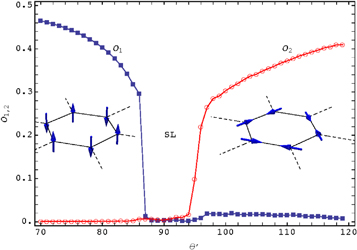
Figure 2. Identifying the phases of the tripod model. The plot shows the order parameters O1 (filled squares) and O2 (empty circles) as a function of calculated from the infinite tensor network algorithms with bond dimension D = 8 and 6-sites unit cell. The insets illustrate the schematic spin configurations in the Néel ordered phase (left) and the dimer phase (right) for a hexagon. For , the spin averages are zero, and the ground state is identified as a spin liquid.
Download figure:
Standard image High-resolution image2. The tripod model
We generalize the Kitaev and the model to the following continuum compass model defined on the two-dimensional honeycomb lattice
where , and for each lattice site the spin 1/2 operators are defined as
with the Pauli matrices . Each site is coupled to its neighbors , where , denotes the three bond vectors of the honeycomb lattice. Geometrically, the three form a tripod in the spin space as shown in figure 1: they are tilted from the xz plane by angle θ and, when projected onto the xz plane, are orientated along the corresponding bond direction , i.e. at azimuthal angle respectively. While is most naturally defined through the tilting angle θ, it is much more convenient to introduce another angle, , to discuss the various limits of . is the angle between T1 and T2, i.e., the two adjacent legs of the tripod. And it is related to θ by trigonometry
We will take as the only tuning parameter in the tripod model.
Three special limits of this model can now be identified. First of all, when all collapse to . The tripod is closed, and is nothing but the Ising model
Note that we choose as the vertical axis in spin space instead of the usual convention of so that reduces exactly to the model defined in our earlier work [6]. Secondly, when reduces to the Kitaev model since the operators are now perpendicular to each other in the spin space. We can simply identify them as and (apart from a factor 1/2) in a rotated coordinate system as illustrated in figure 1(b). Thirdly, for becomes the quantum 120◦ with all confined within the xz plane. It can be visualized as a fully open tripod.
As well known, the Ising model has antiferromangetic (AF) order with the order parameter
On the other hand side, the quantum 120◦ model is conjectured to be long-range ordered despite the geometric frustration. We introduce the following 'order parameter' to measure the in-plane magnetization
By solving using tensor network algorithms, we compute the average spin in the ground state. The main results are summarized in the schematic phase diagram in figure 1(b). Figure 2 shows the variation of the two order parameters introduced above as is changed. The region at small corresponds to the familiar Néel order which is characteristic of the classical Ising model and illustrated in the left inset of figure 2. Despite the increased quantum fluctuations as is increased, the Néel ordered phase persists up to . At the opposite end of large , we find that the long-range spin order consists of a set of 'dimers,' i.e. opposite spins on neighboring sites, arranged into a periodic pattern of triangular lattice (figure 5(a)). The triangular lattice and its enlarged unit cell becomes transparent if we introduce a topological charge (red dot in figure 5(a)) for each hexagon with spins all pointing outwards. If we focus on one individual hexagon, e.g. the one shown in the right inset of figure 2, the orientations of the dimers happen to be also 60° (or equivalently 120°) apart. We will refer to this phase simply as the 'dimer phase.' In particular, it is the ground state of the quantum model on honeycomb lattice. This point will be further discussed in section 5.
Sandwiched between the Néel ordered phase and the dimer phase, a quantum SL phase is stabilized for . The conclusion is mainly based on the observation from figure 2 that the order parameters in this region are nearly zero compared to those in other two phases. This conclusion is also consistent with the exactly solution of Kitaev model for . The order parameters as functions of in figure 2 also suggest that the two quantum phase transitions in the tripod model may be qualitatively different. The gradual drop of O2 at indicates a continuous phase transition between the dimer phase and the SL phase. In contrast, the drop of the order parameter O1 at is rather sharp, pointing to a likely first-order phase transition. The details of the calculations leading to these results will be discussed below in section 3.
3. Tensor network algorithms
Recent developments of entanglement-based tensor network algorithms provide a novel, accurate approach to strongly correlated electron systems [25–29]. Particularly, they have been successfully applied to frustrated quantum magnets [19–22] and the t − J model [30, 31] to yield insights previously unattainable from conventional methods. To find the phase diagram of the proposed tripod model, we employ two complementary tensor networks algorithms, one for finite-size systems and the other for infinite systems in the thermodynamic limit, to find the ground state and the order parameters. In both algorithms, the ground state wave function is constructed as a network of local tensors defined on lattice sites. Each tensor has one physical index representing the spin degree of freedom and three virtual indices, each with bond dimension D, describing the quantum entanglement with its three neighboring sites.
We first apply the finite PEPS algorithm [25–27] to solve for a six-site system with periodic boundary conditions. The ground state energies obtained coincide with those from ED. This suggests that PEPS is intrinsically superior compared to mean field theories when applied to frustrated spin Hamiltonians such as . The order parameters decay to zero as the ground state is approached for a finite system. Nonetheless, their decay behaviors are quite disparate for values in the Ising, Kitaev, and regions, suggesting three different phases. The details of the calculation are presented in appendix
To study the tripod model in the thermodynamic limit, we first find the converged ground state using imaginary time evolution and following the simple update scheme as described in [32] which generalizes the time-evolving block decimation (TEBD) [33] technique to two-dimensions. For a n-site unit cell, e.g. a six-site unit cell shown in figure 3(a), we need different bond vectors that represent, roughly speaking, a mean-field approximation of the environment. Using these bond vectors, the simple update starts with n random tensors and iterates until convergence is achieved. At the end of the calculation, the ground state is characterize by n tensors . We then evaluate the expectation value of operator which involves the (infinite) product of tensors Tj, using a real space coarse graining procedure known as higher-order TRG (HOTRG) [24] schematically shown in figure 3. We outline the main steps here. At the ith step of HOTRG, a local tensor, say Ti1, is regrouped with its three nearest neighbor tensors () to form a new tensor . More generally, for odd or even sites
where the summation is over the shared legs (abbreviated as s.l., the solid lines in figure 3(b)) of the neighboring tensors, i.e. tensor contractions. The new tensors, each of which contains four old tensors, are of higher dimensions and truncated to have the same dimension as Ti via
where the three projection tensors , shown in figure 3(b), are obtained as follows. Take Ux as an example. First, is reshaped into matrix with the row corresponding to the leg along the x-direction. Then, a matrix is obtained by singular value decomposition
Finally, Ux is obtained by truncating to a given truncation dimension χ and reshaping it back to the tensor form. The new tensors now form exactly the same honeycomb lattice structure as the old tensors Ti but represent a larger system, see figure 3(c). This constitutes a single RG step. By iterating the RG steps many times, the converged result of well approximates the expectation value in the thermodynamic limit.
Figure 3. The HOTRG procedure used to calculate the expectation value after the convergence of the ground state. (a) The unit cell (the center hexagon) consists of six sites. Associated with each site is a local tensor Tij at the ith RG step. (b) The coarse graining procedure to construct the new tensor from the old tensors Ti1 and its neighbors . The other five tensors are updated in the similar way. (c) The new tensors again form a honeycomb lattice.
Download figure:
Standard image High-resolution imageBy following these procedures, we have calculated the ground state energy and the ground state expectation values of the order parameters for different unit cell sizes, . We found that the six-site unit cell gives the lowest energy. The two-site unit cell yields results in agreement with the six-site unit cell within the parameter region . The four-site and eight-site unit cells, however, lead to excited states with significantly higher energy. Thus, we conclude that the six-site unit cell is the most reasonable choices for all the values in the ground state calculation. In practice, one can safely use the two-site unit cell for since it is significantly cheaper. The phase diagram and the spin configurations in the ordered phases shown in figure 2 are obtained by using the two-site unit cell for and the six-site unit cell for .
4. Spin wave analysis
To cross-check the TRG results, we perform the standard spin wave analysis of the tripod model. It is important to keep in mind that the validity of the spin wave theory, which can be viewed as expansion in series of , becomes questionable in the limit of . Yet the analysis offers a rough picture of the role played by geometric frustration and how the Néel order and dimer order get destroyed by the increased quantum fluctuations. As we will show below, the estimations of the two quantum critical points from the spin wave theory turn out to be in broad agreement with the phase digram predicted by the tensor network algorithms.
The analysis starts by partitioning the honeycomb lattice into the A and B sublattice and introducing for all sites on the A (B) sublattice. Then the tripod Hamiltonian acquires a suggestive form
Here we have promoted the spin 1/2 operator to general spin operator with spin quantum number S. It follows that classical ground states are massively degenerate (except for the Ising limit). Any spin configurations with , i.e., the projection of along the bond direction being the same for any two neighboring sites, will minimize the classical energy. This is a well known feature of compass models, see the review [1]. The special case of the classical model on honeycomb lattice was previously discussed in [7, 34]. We will confine our spin wave analysis to the simple case of spatially homogeneous spin configurations as done in [34]. The direction of is characterized by its polar angle φ measured from and its azimuthal angle α of measured from in – plane. The corresponding classical ground state energy per unit cell is
It is interesting to note that, coincidently, at the Kitaev point, which corresponds to is completely flat and does not depend on φ. For is minimized when or π, corresponding to the two degenerate states with spin up or down in the Néel ordered phase. In contrast, for is minimized when , i.e., lies within the – plane. Therefore, the mean field theory above predicts that the tripod model has a phase transition exactly at the Kitaev point.
Applying the Holstein–Primakoff transformation [35] to and expanding the resulting Hamiltonian of bosons to order , we compute the quantum fluctuation correction to the ground state energy for the two long-ranged ordered states respectively and find
where is the number of sites within the A sublattice, the summation is over the first Brillouin zone of the A sublattice, and describe the spin wave dispersion for branch and they are given by the eigenvalues of the matrix
The expressions for and are lengthy and tabulated in appendix
The results for from the spin wave analysis are plotted in the upper panel of figure 4 for several values of corresponding to the Néel ordered phase. One notices that the fluctuations do not change qualitatively the mean field ground state. reaches minima still at or π for small . However, as is increased, the energy becomes flatter. Eventually, as (the top curve of figure 4), the energies for with proper choice of α become degenerate with those for . This signals the destabilization of the Néel order by quantum fluctuations. This occurs around , before the Kitaev point is approached. Note that in figure 4, only the region is shown. Outside this region (and also for ), the lowest order spin wave theory based on the Ising-like antiferromagnetic order becomes ill defined.
Figure 4. The energy per unit cell from leading order spin wave theory for the tripod model. Upper panel: for the Néel ordered phase. At , the location and number of minima of E change, indicating the transition to a different phase. Lower panel: for the dimer phase with minima occurring at . At the critical point changes qualitatively, signals another phase transition.
Download figure:
Standard image High-resolution imageFor , the classical ground state is continuously degenerate with but arbitrary . Quantum fluctuations lift the degeneracy and select a long-range ordered ground state via the 'order by disorder mechanism'. Such mechanism for the special case of , i.e. the quantum 120◦ model, has been discussed before in [6, 7, 34]. As shown in the lower panel of figure 4, the same physical picture continues to hold for the tripod model for : the energy E is minimized at with integer n. However, becomes increasingly flat as is decreased. At the critical point , additional minima of E appear at . This indicates that the long-range order gets destroyed and replaced by a new phase for .
We emphasize that the simple version of spin wave theory outlined above is only intended to estimate the lower and upper critical points for the SL phase, and . It can be further improved to properly treat general classical spin configurations. We will not do it here because the large S expansion by itself cannot unambiguously determine the order for our model of in the region .
5. The dimer phase
Previous theoretical studies of the quantum model on the honeycomb lattice gave conflicted results. The spin wave analysis of [6] assumed a homogenous ground state and found quantum fluctuations prefer . This led the authors to suggest that the ground state may be a simple ferromagnet of with any choice of (i.e. antiferromagnetic order in terms of the original spin or ). Reference [7] considered more general (inhomogeneous) classical ground states and discovered that, within spin wave theory, the ferromagnetic state is energetically less competitive than a 'fully packed unoriented loop configuration' with the same values. The reason is quite subtle but argued to be physically robust: the loop configuration hosts maximum number of zero modes. This result obtained from semiclassical large-S expansion was conjectured to survive in the limit of , i.e. the quantum model has a ground state with the six-site plaquette order [7]. However, no evidence of long-range order was found in ED studies where the spin correlation functions were computed for finite size clusters with periodic boundary conditions [34]. Instead, the ED results supported a trial wave function similar in spirit to the short-range resonating valence bond state, i.e., a liquid state with linear superposition of dimer covering of the lattice. Therefore, the true ground state of the quantum model was not settled.
Compared to these previous works, the numerical tensor network algorithm used here takes into account quantum fluctuations beyond the lowest order spin wave theory, works directly in the thermodynamic limit, and starts with unbiased (random) choice of tensors as variational parameters. It is capable of describing both the long-range ordered and the spin-disordered ground states. We find the ground state of the quantum model is the dimer phase illustrated in figure 5(a) where the arrows denote the direction of spin average on each site, and the numbers indicate the bond energies in unit of J. The long-range spin order we observed agrees with the conjecture based on physical insights in [7].
Figure 5. Configurations for (a) the dimer phase () and (b) the spin liquid phase () of the tripod model. The number associated with each bond is , i.e. the bond energy in unit of J, from HOTRG calculation. The arrows in (a) depict the spin direction on each site.
Download figure:
Standard image High-resolution imageWe prefer the shorter, more descriptive name of 'dimer phase' adopted here because it indicates a solid (crystal) order of 'dimers', i.e. antiferromagnetically aligned spins along the bond direction, on a subset of the bonds. We propose to describe the long-range order using the vorticity or the winding number of the spin configuration around each hexagon
where j labels the six sites of the hexagon. For example, hexagons marked by a dot in the center in figure 5(a) correspond to where all spins on the vertices point radially outwards (corresponding to the 'loop' in [7]). The rest of the hexagons, each marked by a cross at the center, have . It then becomes apparent that the hexagons marked by dots form a triangular lattice of spin vortices. And within one unit cell of the triangular lattice, the total vorticity is zero. Note that the state shown in figure 5(a) is energetically degenerate with a state where all the spins are flipped.
By embedding the quantum model into the more general tripod model, we are able to monitor the suppression of the dimer order and its eventual transition into the gapless SL phase (phase B) of the Kitaev model. The results are summarized in figure 6. We observe that the in-plane magnetization O2 decreases continuously to zero as is reduced. Meanwhile, the ground state energy E steadily rises, indicating an increased degree of frustration as the Kitaev point is approached. One can measure the dimer order by introducing the energy difference between the averages of two types of bonds: the 'happy' bonds (dimers) with antiparallel spins and the frustrated bonds where the two spins form an angle of 60°. Therefore, the dimensionless parameter
can also serve as the order parameter for the dimer phase. As plotted in figure 6, η continuously drops to zero as is reduced from to 95°. Once inside the SL phase, both O2 and η vanish, and the bond energies become approximately the same (see figure 5(b)). One can view the transition from the SL to the dimer phase as condensation of spin vortices. Equivalently, when is reduced, one can view the demise of the dimer order as the melting of the spin vortex lattice. Note the bond energy shown in figure 5 features small fluctuations and does not strictly obey C6 rotation symmetry. In our tensor network calculations, no spatially symmetry is enforced on the tensors, and the expectation values of operators are computed approximately. The fluctuations are expected to decrease as the bond dimension is increased.
Figure 6. The order parameters of the dimer phase, O2 and η (defined in the main text), and the ground state energy E as functions of . The vanishing of O2 and η marks the transition from the dimer phase to the spin liquid phase.
Download figure:
Standard image High-resolution image6. Potential realization
The tripod model can be realized from the following Hubbard model at half filling in the Mott limit
where annihilates a fermion with spin σ at site i. The direction and spin dependent hopping matrix is related to defined in equation (2) simply by
Explicitly, they are given by
where we have suppressed the superscript γ for brevity, and
In the limit of , using second-order perturbation theory, we obtain the following effective Hamiltonian for
which is nothing but the tripod model , up to a constant term, with the superexchange . Note that the derivation of the effective compass Hamiltonian above does not depend on the details of the parameterization of in terms of θ and . It follows that a large class of compass models, not limited to the tripod model proposed here, can be engineered on honeycomb lattice following the recipe above.
Duan et al previously showed that the Kitaev model can be realized using cold atoms on a hexagonal optical lattice with extra laser beams [36]. Generalization of their idea to the case of the tripod model (and other compass models) requires spin-dependent hopping controlled by a non-Abelian gauge field or generalized spin–orbit coupling. Schemes to realize spin–orbit coupling was proposed in various approaches [37–40]. The realization of many have been demonstrated successfully in cold atoms experiments [41–44]. For example, spin-dependent optical lattices have been engineered using magnetic gradient modulation [44–46]. It seems possible, but challenging, to make spatially dependent. Alternatively, the tripod model proposed here may be emulated using other artificial quantum systems such as superconducting quantum circuits [47].
7. Outlook
The tripod model introduced in this paper encompasses three well known models of quantum magnetism: the Ising model, the Kitaev model and the 120° model. We established its (zero temperature) phase diagram using tensor network algorithms. This amounts to solving a continuum of frustrated spin models with spatially dependent exchange interactions. In particular, we found an extended SL phase around the Kitaev point, and a dimer phase for large values of angle including the quantum 120° model. The two quantum critical points obtained from tensor network states agree roughly with estimations from spin wave theory.
Our work only scratches the surface of the rich physics contained in the tripod model. Here we mention just a few open questions to be addressed in future work. First of all, it is desirable to develop a fieldtheoretical description of the continuous phase transition between the SL phase and the long-range ordered dimer phase, based on the intuitive picture of spin vortices introduced in section 5. Secondly, the tripod model, like other compass models, has very interesting emergent symmetry properties including intermediate symmetries midway between the global and local symmetries [1]. Consequently, the excitation spectrum is expected to contain zero modes and/or flat bands. It is therefore valuable to understand the excitation spectra of the long-range order phases by going beyond the ground state analysis here. Thirdly, the finite temperature properties of the tripod model deserve a separate study. The classical limit of the tripod model is known to be highly nontrivial. The effects of thermal fluctuations and the 'order by disorder' mechanism have been investigated in [34] for the classical 120° model. Finally, we have only focused on the case of here. From the Kitaev model, we know that a gapped SL phase (phase A) takes over when the asymmetry in Jγ grows large. Thus one expects that further generalization of the tripod model to general values of Jγ may uncover new interesting phases.
To conclude, we hope our results can stimulate further application of tensor network algorithms to frustrated spin models as well as spin–orbital models describing transition metal oxides. We also hope our introduction of the tripod model can inspire alternative proposals to extend the Kitaev model or realize compass models in artificial quantum systems such as cold atoms on optical lattices or superconducting circuits.
Acknowledgments
We thank Jiyao Chen, Arun Paramekanti, Zhiyuan Xie, and Congjun Wu for helpful discussions. This work is supported by AFOSR Grant No. FA9550-16-1-0006 (HZ, BL, EZ, and WVL), NSF Grant No. PHY-1205504 (HZ and EZ), and jointly by US ARO Grant No. W911NF-11-1-0230, the Pittsburgh Foundation and its Charles E Kaufman Foundation, and the Overseas Scholar Collaborative Program of NSF of China No. 11429402 sponsored by Peking University (WVL). WVL is grateful for the hospitality of KITP UCSB where part of this manuscript was written with support from NSF PHY11-25915. Publication of this article is funded by the George Mason University Libraries Open Access Publishing Fund, and the University Library System, University of Pittsburgh.
Appendix A.: Tensor network algorithms
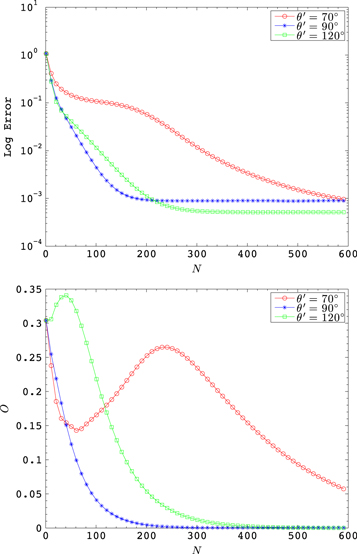
The finite PEPS algorithm is a powerful numerical approach for two-dimensional quantum spin systems [25–27]. For the tripod model, we construct the usual PEPS wave function starting from six random rank-four tensors with virtual bond dimension D = 3. The tensors are then optimized through recursive imaginary-time evolution with time step on all the links. Once the wave function is converged, we calculate the ground state energy and the expectation value of the combined order parameter . The results are shown in figure 7 for three typical values of (corresponding to the three different phases found in the thermodynamic limit). For the small system size considered here (six sites with periodic boundary conditions), O vanishes as the wave function converges to the ground state. Nonetheless, a noticeable peak of O during the time evolution can serve as the indication for spin order. For all the three cases, the energies converge to the ED result up to a relative error of 10−3 (the upper panel of figure 7). The peaks of O in the lower panel of figure 7 for the cases and point to the Néel order phase and the dimer phase respectively, while the monotonic decay of O for the case suggests a SL state.
Figure 7. Finite PEPS results for a six-site cluster showing the errors of ground state energy (relative to that from the exact diagonalization) and the order parameter O for three different values of .
Download figure:
Standard image High-resolution imageWithin the many variants of tensor network algorithms, a typical way to find the phase diagram of quantum spin models is the infinite PEPS (iPEPS) method [28, 29]. The iPEPS ansatz on the honeycomb lattice usually proceeds by mapping the lattice to a square lattice and evaluating the effective environment by contraction schemes such as infinite matrix product states [28] or corner transfer matrices [48, 49]. For instance, the phases of Kitaev–Heisenberg model [50] and the SU(4) symmetric Kugel–Khomskii model [51] have been studied via the iPEPS ansatz with a 2 × 2 or 4 × 4 unit cell. However, the contraction scheme for a six-site (hexagonal) unit cell on the honeycomb lattice is tedious and expensive, especially for the corner transfer matrices scheme.
For this reason, we adopt the simple tensor update scheme and evaluate the contraction using the HOTRG method as explained in the main text. The simple update [32] generalizes the TEBD [33] technique to two-dimensional quantum systems by introducing the bond vectors to represent the mean-field environment for local tensors. We set the imaginary time step and the number of iterations is generally around 105 (smaller time step does not improve the numerical result significantly). The accuracy of the HOTRG method is controlled by the virtual bond dimension D. By systematically increasing D, the quantum entanglement between neighboring sites is better taken into account, yielding a more accurate ground state. For example, figure 8 shows that the order parameter O2 vanishes when D is increased to 8 in the region , suggesting a SL ground state. One notices that the variations of the ground state energy with within the SL phase is larger than those in the long-range ordered phase, especially for smaller D values. This is due to the strong quantum fluctuations intrinsic to the SL. Cross-checking the HOTRG calculations here to those using Second Renormalization Group [52] which takes into account the entanglement between the system and the environment deserves a future study.
Figure 8. The ground state energy E and the order parameter O2 computed from HOTRG at virtual bond dimension and truncation dimension .
Download figure:
Standard image High-resolution imageAppendix B.: Spin wave theory
For the two long-range ordered phases, the corrections to the energy are obtained by diagonalizing the matrix equation (14) with different form factors , and . For the Néel ordered phase, they are given by
And for the dimer phase
Here, aj and bj are related to the parameter , and α defined in the main text through
Footnotes
- 5
In this paper, we use the term 'spin liquid' to denote a phase that shows no long-range spin order according to our tensor network algorithms. At the special point, the tripod model reduces to the Kitaev model and its ground state is well established to be a gapless spin liquid. Our numerical results offer evidence that the same spin-liquid state will survive away from the Kitaev point. The nature of the excitations (e.g. their fractional statistics) remains to be checked in order to firmly establish that it is a quantum spin liquid.



























![${\theta }^{\prime }\in [87^\circ ,94^\circ ]$](https://content.cld.iop.org/journals/1367-2630/18/5/053040/revision1/njpaa22dfieqn23.gif)










































![${\theta }^{\prime }\in [87^\circ ,94^\circ ]$](https://content.cld.iop.org/journals/1367-2630/18/5/053040/revision1/njpaa22dfieqn60.gif)











![${T}_{j},j\in [1,n]$](https://content.cld.iop.org/journals/1367-2630/18/5/053040/revision1/njpaa22dfieqn72.gif)












































































![$\varphi \in [0,\pi /4]\cup [3\pi /4,\pi ]$](https://content.cld.iop.org/journals/1367-2630/18/5/053040/revision1/njpaa22dfieqn140.gif)









![$\alpha \in [0,2\pi ]$](https://content.cld.iop.org/journals/1367-2630/18/5/053040/revision1/njpaa22dfieqn149.gif)