Abstract
We consider the usage of dynamical decoupling in quantum metrology, where the joint evolution of system plus environment is described by a Hamiltonian. We show that by ultra-fast unitary control operations acting locally only on system qubits, noise can be eliminated while the desired evolution is only reduced by at most a constant factor, leading to Heisenberg scaling. We identify all kinds of noise where such an approach is applicable. Only noise that is generated by the Hamiltonian to be estimated itself cannot be altered. However, even for such parallel noise, one can achieve an improved scaling as compared to the standard quantum limit for any local noise by means of symmetrization. Our results are also applicable in other schemes based on dynamical decoupling, e.g. the generation of high-fidelity entangling gates.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Quantum mechanics offers the promise to significantly enhance the precision of estimating unknown parameters as compared to any classical approach [1–3]. Such high-precision measurements are of central importance in physics and other areas of science, and include possible applications in frequency standards [4–6], atomic clocks [7–9], or gravitational wave detectors [10, 11]. Whereas the quantum advantage can survive in the presence of some particular noise types [12, 13], it can not be maintained in the presence of a general incoherent noise processes [5, 14–23].
Identifying schemes that realize this advantage in practice are of high theoretical and practical relevance. It was shown that quantum error correction [23–26], dynamical decoupling [27, 28] or limited control over the environment [29, 30] allow for an improved scaling for certain, specific noise processes.
Here we consider the usage of dynamical decoupling techniques [31–34] for quantum metrology. These techniques have been shown to be applicable in the context of storage or for the realization of quantum gates [35, 36], and are nowadays widely used in various experimental settings [37–45]. We show that with the help of ultra-fast control operations that act locally on the system qubits, one can effectively decouple the system from its environment and fully protect it against decoherence effects, while at the same time maintaining its sensing capabilities and its quantum advantage in metrology. We identify all noise processes that can be eliminated, and discuss additional techniques that allow one to obtain a super-classical scaling even in situations where these methods are not applicable. Our systematic investigation of which kinds of noise are correctable is also applicable in different contexts, e.g. for the realization of high-fidelity quantum gates using dynamical decoupling techniques [35, 36].
System and environment interact via a coherent evolution governed by some Hamiltonian HSE. In addition, the sensing system is effected by a Hamiltonian HS that includes an unknown parameter that should be estimated. We assume that a coherent description is appropriate at all times, and that the evolution can be interrupted by fast control operations. This is similar to what is done in dynamical decoupling [31, 32, 35, 36, 46], with the requirement that the desired evolution is not cancelled. In addition we do not enforce the evolution to be left invariant, but allow it to be altered in a controlled way. In practice, these intermediate pulses will not be infinitely fast, and only noise up to a certain frequency can be treated and eliminated this way. However, in what follows we will assume that the accessible time is much faster than any other timescale in the problem.
Our main findings are summarized below:
- (1)We show that for any local system-environment interaction of rank one or two one can completely eliminate the noise process at the cost of reducing the sensing capabilities of the system by a constant factor leading to Heisenberg scaling in precision. Only interactions that are of rank three—and hence necessarily contain a component that is generated by the system Hamiltonian that should be estimated—cannot be fully corrected.
- (2)Still one can achieve that only this parallel noise part remains, and, even in this case one can still maintain a quantum advantage. In particular, for any local noise process, we show that one can achieve a super-standard quantum scaling in precision by preparing N qubit probes in the Greenberger–Horne–Zeilinger (GHZ) state and randomizing the qubits via fast, intermediate swap gates.
- (3)For correlated noise processes we provide a general lower bound on the achievable precision, applicable even if one assumes perfect quantum control and auxiliary resources, demonstrating that one is in general restricted to the standard quantum limit (SQL). Even in this case, one may still improve the precision by a constant factor, though the effect depends on the details of the system-environment interactions and the type of fluctuations.
- (4)Finally we demonstrate that that our results are applicable in the design of high-fidelity quantum gates for fault-tolerant quantum computation.
2. Background
Quantum metrology is the science of optimally measuring and estimating an unknown parameter such as the frequency in an atomic clock or the strength of a magnetic field. In a typical metrology scenario, a system of N probes evolves for time t under the Hamiltonian  , where ω is the parameter to be estimated, and is subsequently measured. This process is repeated ν times and ω is estimated from the measurement statistics. The Cramér–Rao bound provides a limitation on the estimation precision
, where ω is the parameter to be estimated, and is subsequently measured. This process is repeated ν times and ω is estimated from the measurement statistics. The Cramér–Rao bound provides a limitation on the estimation precision  , which is attainable for large enough number of repetitions ν. Here
, which is attainable for large enough number of repetitions ν. Here  is the quantum Fisher information (QFI) [47]. For classical strategies (separable probe states) the ultimate precision is given by the SQL,
is the quantum Fisher information (QFI) [47]. For classical strategies (separable probe states) the ultimate precision is given by the SQL,  . Using entangled states, one can achieve the so-called Heisenberg limit,
. Using entangled states, one can achieve the so-called Heisenberg limit,  , i.e., a quadratic improvement as compared to any classical strategy [1–3].
, i.e., a quadratic improvement as compared to any classical strategy [1–3].
However, in practice the system is not isolated but also interacts with its environment. In general, this leads to a noisy evolution, where it was shown that in case of incoherent noise described by a master equation, the quantum advantage is limited to a constant factor rather than a different scaling [15–22]. The way to describe noise processes crucially depends on the timescales of the problem. Here we assume that we have ultra-fast access to the system, and can interject the evolution by control operations, faster than the relaxation time of the environment. In this case it is appropriate to describe the dynamics of system plus environment in a coherent way, i.e., by means of an overall Hamiltonian that governs the unitary evolution. As we will show shortly, the fact that system and environment evolve coherently grants us with additional freedom that allows to maintain Heisenberg scaling even in the presence of uncontrolled interaction with some environment.
3. General setting
We begin by first considering the case of a single qubit. The most general evolution of a single qubit plus environment is described by the Hamiltonian

where  describes the evolution of the system, HSE describes the system-environment interaction with Aj arbitrary environment operators and cj the coupling strengths. Here and throughout the remainder of this work
describes the evolution of the system, HSE describes the system-environment interaction with Aj arbitrary environment operators and cj the coupling strengths. Here and throughout the remainder of this work  denote the Pauli matrices,
denote the Pauli matrices,  denotes the vector of Pauli matrices and
denotes the vector of Pauli matrices and  .
.
In the case where we have N probe systems, the exact form of the Hamiltonian governing their coherent evolution with the environment depends on whether the N probes couple to individual environments, or to a common environment. In the former case the Hamiltonian is given by
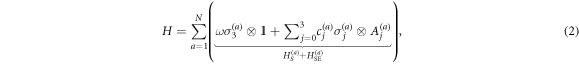
where  act on different Hilbert spaces. If the N probes couple to a common environment the
act on different Hilbert spaces. If the N probes couple to a common environment the  act on the same Hilbert space and might even be equal for all a in the extreme case.
act on the same Hilbert space and might even be equal for all a in the extreme case.
4. Decoupling strategy
The most general dynamical decoupling strategy consists of applying an arbitrarily fast time sequence of unitary gates  applied at times
applied at times  , i.e., intersecting the system evolution with fast pulses. If this is done fast enough, one can use a first order Trotter expansion to describe the effective evolution as being generated by the Hamiltonian
, i.e., intersecting the system evolution with fast pulses. If this is done fast enough, one can use a first order Trotter expansion to describe the effective evolution as being generated by the Hamiltonian

modulo an irrelevant final unitary, where we redefine the gates as  and the probabilities are obtained from the time sequence
and the probabilities are obtained from the time sequence  . This is similar to what is done in optimal control theory or bang-bang control [31, 32], with the requirement that the desired evolution HS is not completely eliminated. For the simple case of orthogonal
. This is similar to what is done in optimal control theory or bang-bang control [31, 32], with the requirement that the desired evolution HS is not completely eliminated. For the simple case of orthogonal  noise, fast intermediate
noise, fast intermediate  operations suffice (see [28]).
operations suffice (see [28]).
The applicability of dynamical decoupling techniques is determined by the timescales of the problem. We are considering a situation where control operations can be performed infinitely fast. This is a standard assumption in optimal control theory [31, 32], and justifies the expansion in equation(3) leading to the effective Hamiltonian. The requirements on the applicability of the first order Taylor expansion, i.e., the requirement on the frequency of intermediate control operations, depend on the spectral radius of the Hamiltonian (and thus the number of systems N). In addition, in order to write the effective Hamiltonian as a coherent sum of terms for different times it is important that the environment operators and the coupling terms do not change. This provides the condition that control operations need to be much faster than all relevant relaxation timescales of the environment. We would like to point out, though, that methods in dynamical decoupling techniques have been developed where this stringent assumption of infinite fast control, or in turn a restriction of results to noise up to a certain frequency for any given control rate, can be significantly softened [48].
5. Single qubit
In the single qubit case the parametrization of completely positive trace preserving (CPTP) maps in equation (3) spans exactly all the unital maps, i.e. such that  [49], and any unital map can be constructed with the set of four gates
[49], and any unital map can be constructed with the set of four gates  . As all single qubit CPTP maps corresponds to affine transformations on the Bloch sphere, a unital CPTP map is uniquely specified by a real matrix
. As all single qubit CPTP maps corresponds to affine transformations on the Bloch sphere, a unital CPTP map is uniquely specified by a real matrix  , where
, where  ,
,  (the values
(the values  have to satisfy several constraints which are, however, not important in our context), and the action of such map on any Pauli matrix is given by
have to satisfy several constraints which are, however, not important in our context), and the action of such map on any Pauli matrix is given by  . The second rotation
. The second rotation  corresponds to an inconsequential change of basis, so we assume
corresponds to an inconsequential change of basis, so we assume  .
.
Accordingly, a noise term is completely eliminated by the dynamical decoupling strategy if and only if it belongs to the kernel of the corresponding matrix  : if a noise term belongs to the kernel it is eliminated by the action of DR, while if it does not at least a part of it remains after the application of the dynamical decoupling sequence. On the other hand
: if a noise term belongs to the kernel it is eliminated by the action of DR, while if it does not at least a part of it remains after the application of the dynamical decoupling sequence. On the other hand  since some part of the system evolution has to survive. Therefore to identify all the noises that can be removed it is sufficient to consider rank one projectors
since some part of the system evolution has to survive. Therefore to identify all the noises that can be removed it is sufficient to consider rank one projectors  on a general direction
on a general direction  . It follows that the action of the corresponding map
. It follows that the action of the corresponding map  on Pauli matrices is given by
on Pauli matrices is given by  . Notice that this remains true even if one allows for auxiliary systems and intermediate unitary operations in equation (3) to act on the enlarged system. Even when embedded in a larger vector space (spanned by operators which could also act on auxiliary qubits), the support of the evolution and of the noise operators is still on a subspace that has the same dimension as the initial space. Hence, the purely geometrical argument regarding which type of vectors can be eliminated is still valid even when using higher-dimensional vectors that form a subspace of the same dimension as the initial space. Finally note that a unital map
. Notice that this remains true even if one allows for auxiliary systems and intermediate unitary operations in equation (3) to act on the enlarged system. Even when embedded in a larger vector space (spanned by operators which could also act on auxiliary qubits), the support of the evolution and of the noise operators is still on a subspace that has the same dimension as the initial space. Hence, the purely geometrical argument regarding which type of vectors can be eliminated is still valid even when using higher-dimensional vectors that form a subspace of the same dimension as the initial space. Finally note that a unital map  can be easily implemented by applying
can be easily implemented by applying  at regular intervals, so that the effective Hamiltonian is
at regular intervals, so that the effective Hamiltonian is  .
.
Now we identify all the noises that can be removed by dynamical decoupling. The noise term  in equation (1) only acts on the environment and cannot be altered by control operations performed on the system. In what follows we will ignore this term. The action of the decoupling strategy
in equation (1) only acts on the environment and cannot be altered by control operations performed on the system. In what follows we will ignore this term. The action of the decoupling strategy  on the rest of the Hamiltonian in equation (1) leads to
on the rest of the Hamiltonian in equation (1) leads to
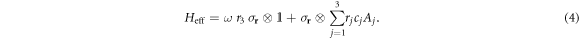
Consequently the noise can be effectively decoupled if and only if  such that
such that  in which case the effective system evolution is slowed down by the factor
in which case the effective system evolution is slowed down by the factor  .
.
In the case of bounded operators Aj the Hamiltonian equation (1) can be put in the standard from

where  ,
,  is an orthonormal frame and
is an orthonormal frame and  are the ordered Schmidt coefficients, see supplementary material. This allows a more intuitive geometrical picture of dynamical decoupling. For any rank one or two noise, i.e.
are the ordered Schmidt coefficients, see supplementary material. This allows a more intuitive geometrical picture of dynamical decoupling. For any rank one or two noise, i.e.  , we can choose
, we can choose  , orthogonal to the plane where noise acts. The fact that the desired evolution
, orthogonal to the plane where noise acts. The fact that the desired evolution  is not completely canceled requires that
is not completely canceled requires that  , which is equivalnet to
, which is equivalnet to  . In this case, the noise is completely eliminated by dynamical decoupling and, as above, the system evolution
. In this case, the noise is completely eliminated by dynamical decoupling and, as above, the system evolution  is slowed down by a factor
is slowed down by a factor  .
.
The decrease of the coupling strength leads to a constant reduction of the achievable accuracy by  but, as all noise is completely eliminated, we still obtain Heisenberg scaling precision3
. Notice that noise that is perpendicular to the system Hamiltonian, i.e., any combination of
but, as all noise is completely eliminated, we still obtain Heisenberg scaling precision3
. Notice that noise that is perpendicular to the system Hamiltonian, i.e., any combination of  and
and  noise, can be eliminated without altering the evolution, i.e.
noise, can be eliminated without altering the evolution, i.e.  . This is done by using fast intermediate
. This is done by using fast intermediate  pulses.
pulses.
6. Single qubit and full rank noise
From the above geometrical argument, it follows that one cannot eliminate rank three noise as such noise spans the whole three-dimensional space. To see this note that the effect of the decoupling procedure on any rank-three noise model is to project both the system Hamiltonian and noise onto direction  , so one obtains an effective Hamiltonian equation (4) for system plus environment which is unitarily equivalent to a
, so one obtains an effective Hamiltonian equation (4) for system plus environment which is unitarily equivalent to a  evolution and parallel noise, with
evolution and parallel noise, with  for the standard form. As noise generated by the same operator as the system Hamiltonian cannot be eliminated without eliminating the system evolution as well, the best one can hope for in this case is to reduce any rank-three noise to noise parallel to the system evolution.
for the standard form. As noise generated by the same operator as the system Hamiltonian cannot be eliminated without eliminating the system evolution as well, the best one can hope for in this case is to reduce any rank-three noise to noise parallel to the system evolution.
The choice of direction  in equation (4) determines both the effective coupling strength of the system Hamiltonian r3 and the strength of the noise. One can then choose
in equation (4) determines both the effective coupling strength of the system Hamiltonian r3 and the strength of the noise. One can then choose  to optimize the ratio between the modified coupling strength r3 and the variance of noise fluctuations after projection. Notice, however, that while this shows that in general we can reduce the problem to parallel noise it is not clear if this reduction to parallel noise does in fact correspond to the optimal strategy. Later on we will show what this optimal ratio is for the case of local Gaussian noise.
to optimize the ratio between the modified coupling strength r3 and the variance of noise fluctuations after projection. Notice, however, that while this shows that in general we can reduce the problem to parallel noise it is not clear if this reduction to parallel noise does in fact correspond to the optimal strategy. Later on we will show what this optimal ratio is for the case of local Gaussian noise.
7. N qubits
We now turn to the case of N two level systems. Consider first the case where each qubit encounters an independent environment which corresponds to a local noise process. The total Hamiltonian describing the evolution of all N qubits plus environment is given by equation (2), with the system evolution  , and the system-environment interaction
, and the system-environment interaction  . One can use the above dynamical decoupling strategy independently on each of the systems so that the results of the previous section directly apply. For each qubit, noise of rank one or two can be eliminated, while full rank noise can be reduced to parallel noise
. One can use the above dynamical decoupling strategy independently on each of the systems so that the results of the previous section directly apply. For each qubit, noise of rank one or two can be eliminated, while full rank noise can be reduced to parallel noise  with
with  (and
(and  ).
).
In addition, one can randomize the system particles by means of fast intermediate permutations. Such permutations leave HS unchanged, but project out all asymmetric noise terms onto their symmetric contribution. For single-body noise terms (where each term only acts non-trivially on one of the qubits) such symmetrization is achieved by applying a circular shift at regular time intervals, and each shift can be realized by a sequence of  two-qubit swap gates acting on all pairs of neighboring qubits one after the other. This follows from the fact that after N circular shifts the qubits are back to their initial position, and each qubit was coupled to each local environment for the same duration. Hence, the remaining effective noise term is given by
two-qubit swap gates acting on all pairs of neighboring qubits one after the other. This follows from the fact that after N circular shifts the qubits are back to their initial position, and each qubit was coupled to each local environment for the same duration. Hence, the remaining effective noise term is given by
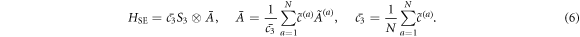
Notice that in general  depends on the individual coupling strengths
depends on the individual coupling strengths  unless all
unless all  are identical. As we show later symmetrization of all system qubits can, in the presence of independent couplings or fluctuating coupling strengths, help boost precision to super-classical scaling. We remark that if the noise has no symmetric contributions then
are identical. As we show later symmetrization of all system qubits can, in the presence of independent couplings or fluctuating coupling strengths, help boost precision to super-classical scaling. We remark that if the noise has no symmetric contributions then  , and even locally full rank noise can be eliminated by symmetrization.
, and even locally full rank noise can be eliminated by symmetrization.
We now consider the case where the N qubits couple to a common environment, which may possess both temporal and spatial correlations, i.e., the operators  in equation (2) are arbitrary. Suppose first that the system-environment interactions are such that each system qubit interacts individually with the environment. Then a strategy similar to the single-qubit case can be applied, where one eliminates all noise except the one generated by the (symmetrized) system Hamiltonian itself. By way of example consider the following local decoupling strategy where one applies fast local
in equation (2) are arbitrary. Suppose first that the system-environment interactions are such that each system qubit interacts individually with the environment. Then a strategy similar to the single-qubit case can be applied, where one eliminates all noise except the one generated by the (symmetrized) system Hamiltonian itself. By way of example consider the following local decoupling strategy where one applies fast local  on each of the qubits. This allows to eliminate all noise terms including
on each of the qubits. This allows to eliminate all noise terms including  without altering HS, and together with fast random permutations reduces all noise to one generated by the system Hamiltonian itself, see equation (6). The only difference as compared to the case of independent environments treated above is that now the operators
without altering HS, and together with fast random permutations reduces all noise to one generated by the system Hamiltonian itself, see equation (6). The only difference as compared to the case of independent environments treated above is that now the operators  may act on the same environment. In general a more involved decoupling strategy requiring non-local operations may be needed in order to partially or fully remove the noise. However, it is not clear if all noise operators except those parallel to HS can be completely removed in this case as not all unital maps can be expressed as convex combinations of unitary operations [50]. Moreover, whatever the dynamical decoupling procedure, the condition that HS has a non-zero overlap with the kernel of the unital map must hold in order to be able to estimate ω.
may act on the same environment. In general a more involved decoupling strategy requiring non-local operations may be needed in order to partially or fully remove the noise. However, it is not clear if all noise operators except those parallel to HS can be completely removed in this case as not all unital maps can be expressed as convex combinations of unitary operations [50]. Moreover, whatever the dynamical decoupling procedure, the condition that HS has a non-zero overlap with the kernel of the unital map must hold in order to be able to estimate ω.
One may also consider noise arising from terms in the Hamiltonian that act on several systems simultaneously (not to be confused with correlated noise terms where different systems couple to the same environment). From a physical standpoint such many-body noise processes are less important as they usually correspond to higher order processes. Nevertheless, thesemany-body noise processes can be eliminated by means of dynamical decoupling, and for any quasi-local noise process one still recovers Heisenberg scaling in the absence of noise generated by S3, see supplementary material.
8. Parallel noise
Hitherto, we have seen how to eliminate all kinds of noise, except noise generated by S3. The latter is indistinguishable from the desired evolution, and cannot be eliminated. However, we will now show that even such parallel noise does not automatically imply the SQL. In fact, the scaling of the QFI depends on the particular situation considered. For instance, for local uncorrelated noise a super-SQL scaling  of the QFI can be achieved, as we show later in this section.
of the QFI can be achieved, as we show later in this section.
Consider the effect of the system plus environment evolution described by equation (6) on the system alone. Tracing out the environment in the eigenbasis  of
of  one can always represent the noise as
one can always represent the noise as

where  corresponds to fluctuations of the interaction strength between experimental runs, and
corresponds to fluctuations of the interaction strength between experimental runs, and  depends on the initial state of the environment (if
depends on the initial state of the environment (if  has a discrete spectrum then the integral over ℓ is replaced by a sum).
has a discrete spectrum then the integral over ℓ is replaced by a sum).
The effect of the system-environment coupling, when the environment is not in an eigenstate of  , is similar to a fluctuating interaction strength. Both cases lead to an ensemble average over evolutions governed by the same Hamiltonian as HS with a random prefactor. This averaging ultimately limits the achievable accuracy, as it corresponds to fluctuations of the parameter ω to be estimated. However, the resulting scaling depends on details, such as the spectrum of environment and whether these fluctuations are correlated or uncorrelated.
, is similar to a fluctuating interaction strength. Both cases lead to an ensemble average over evolutions governed by the same Hamiltonian as HS with a random prefactor. This averaging ultimately limits the achievable accuracy, as it corresponds to fluctuations of the parameter ω to be estimated. However, the resulting scaling depends on details, such as the spectrum of environment and whether these fluctuations are correlated or uncorrelated.
The worst case is when the interaction strength,  , is fixed but unknown. This type of noise leads to a systematic error on the estimated value of ω and there is no way to decrease the error below a certain value set by the initial knowledge of the interaction strength and the state of the environment (except the trivial case where the environment is in the zero eigenstate of
, is fixed but unknown. This type of noise leads to a systematic error on the estimated value of ω and there is no way to decrease the error below a certain value set by the initial knowledge of the interaction strength and the state of the environment (except the trivial case where the environment is in the zero eigenstate of  ).
).
Next consider the case where the mean interaction strength  is known but fluctuates around the mean value between experimental runs following a smooth distribution
is known but fluctuates around the mean value between experimental runs following a smooth distribution  and
and  . This is is equivalent to the case of a fixed
. This is is equivalent to the case of a fixed  but a continuous spectrum of
but a continuous spectrum of  with smooth
with smooth  . We show in the supplementary material that for any
. We show in the supplementary material that for any  the optimal QFI per unit time is upper bounded by
the optimal QFI per unit time is upper bounded by
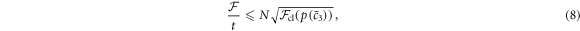
where  remains finite for every smooth noise distribution
remains finite for every smooth noise distribution  enforcing the SQL in this case. For a normal distribution
enforcing the SQL in this case. For a normal distribution  with width σ the bound takes the simple form
with width σ the bound takes the simple form  , whereas a strategy utilizing an N qubit GHZ state
, whereas a strategy utilizing an N qubit GHZ state  gives a maximal QFI per unit time
gives a maximal QFI per unit time  for the optimal choice of t.
for the optimal choice of t.
Next consider local parallel noise, where each  in equation (6) is an independent and normally distributed random variable with width σ. After randomly permuting the probes one finds that
in equation (6) is an independent and normally distributed random variable with width σ. After randomly permuting the probes one finds that  is also a normally distributed random variable whose width is reduced
is also a normally distributed random variable whose width is reduced  . Consequently, preparing the probes in the GHZ state yields a super-SQL scaling
. Consequently, preparing the probes in the GHZ state yields a super-SQL scaling
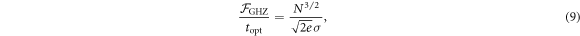
where  . The Cramér–Rao bound
. The Cramér–Rao bound  is attainable for large total running time
is attainable for large total running time  . Hence symmetrization of the probes allows one to significantly reduce the overall effects of noise (as already noted in [51, 52]), and restore super-SQL scaling.
. Hence symmetrization of the probes allows one to significantly reduce the overall effects of noise (as already noted in [51, 52]), and restore super-SQL scaling.
Finally, in the case where  is fixed and
is fixed and  has a discrete spectrum, the effective noise distribution
has a discrete spectrum, the effective noise distribution  is discrete and
is discrete and  is unbounded. Making the bound of equation (8) trivial. No general statements can be made with regards to the optimal QFI per unit time in this case. For example, if
is unbounded. Making the bound of equation (8) trivial. No general statements can be made with regards to the optimal QFI per unit time in this case. For example, if  has an equally gapped spectrum with gap Δ, then at time
has an equally gapped spectrum with gap Δ, then at time  the noise completely cancels. This final example, though artificial, demonstrates that one cannot provide general statements on achievable scaling without specifying further details of the type of fluctuations, interaction, spectrum, and initial state of the environment.
the noise completely cancels. This final example, though artificial, demonstrates that one cannot provide general statements on achievable scaling without specifying further details of the type of fluctuations, interaction, spectrum, and initial state of the environment.
9. Summary and outlook
We have shown that when an overall Hamiltonian description of the system plus environment is appropriate, ultra fast control allow one to alleviate a large class of noise processes, and recover Heisenberg scaling. We remark that the dynamical procedure outlined here are also applicable in other contexts, e.g. for the design of high-fidelity quantum gates we give a sufficient condition for the elimination of the noise in the supplementary material. Ultimately, the only noise processes that forbid Heisenberg scaling precision are those generated by the system Hamiltonian to be estimated itself. The effect of such parallel noise strongly depends on the details of interactions, the spectrum of the environment and the type of fluctuation of the coupling parameter.
Our results are in stark contrast to situations where a master equation description of the system-environment interaction is required. There, it has been shown that with the help of auxiliary systems and fast error correction only rank one Pauli noise processes can be eliminated, while even full quantum control including ultrafast pulses and quantum error correction do not allow one to go beyond SQL scaling [23]. Hence, our results provide a big promise for practical applications of quantum metrology in various contexts, opening the way towards ultra-sensitive devices with widespread potential application in all branches of science.
Finally an interesting question is how our technique can be applied beyond the single-parameter metology scenario studied here. In general, in multi-parameter estimation might the sensing Hamiltonian might contain all three Pauli operators, so the the local dynamical decoupling techniques we described in this paper can not be directly applied (since they would cancel parts of the sensing Hamiltonian). However remark that it is always possible to sense each of the generators separately by dividing the probes in groups and applying the local decoupling strategy on each group separately; in a particular case this strategy was shown to achieve the optimal scaling [53]. Moreover note that the symmetrization technique of section 8 can be applied without modification to any multi-parameter scenario.
Acknowledgments
We thank J Kołodynski for useful discussions. This work was supported by the Austrian Science Fund (FWF): P24273-N16, P28000-N27 and the Swiss National Science Foundation grant P2GEP2_151964.
Appendix A.: Standard form of the Hamiltonian
Consider a Hamiltonian of the form

For bounded operators  we define the overlap matrix
we define the overlap matrix

which is real and symmetric  (as imposed by the hermiticity of the Hamiltonian
(as imposed by the hermiticity of the Hamiltonian  ). Expressing the Pauli operators in a rotated frame
). Expressing the Pauli operators in a rotated frame  allows one to rewrite the Hamiltonian as
allows one to rewrite the Hamiltonian as

with  . Accordingly the overlap matrix for the operators
. Accordingly the overlap matrix for the operators  is given by
is given by

Choosing the rotation that diagonalizes the symmetric matrix  leads to
leads to
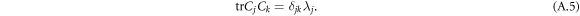
Which also shows that  , being the trace of the square of an Hermitian operator. Finally, denoting
, being the trace of the square of an Hermitian operator. Finally, denoting  and
and  allows one to rewrite the Hamiltonian as
allows one to rewrite the Hamiltonian as
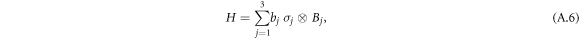
with  .
.
Appendix B.: Correlated noise
We now consider correlated noise processes where several systems are affected jointly. In general, the system-environment Hamiltonian of a N-qubit system is given by  where
where  denotes a tensor product of Pauli operators. Using fast intermediate
denotes a tensor product of Pauli operators. Using fast intermediate  operations on all qubits allows one to eliminate all terms with
operations on all qubits allows one to eliminate all terms with  acting on at least one system qubit. We are then left with a Hamiltonian where
acting on at least one system qubit. We are then left with a Hamiltonian where  and noise is solely diagonal. In case of localized noise, i.e., where there is a certain spatial structure and only qubits that are spatially close are jointly affected by noise, one can use fast intermediate
and noise is solely diagonal. In case of localized noise, i.e., where there is a certain spatial structure and only qubits that are spatially close are jointly affected by noise, one can use fast intermediate  operations acting sparsely to eliminate noise terms of range k. For instance, performing such an action on every second qubit eliminates all nearest neighbor two-qubit noise terms in a 1D setting (acting on every kth qubit eliminates confined k-body noise terms). However, this also eliminates the desired evolution for half of the particles (every kth particle), and these particles no longer contribute to the sensing process. As long as the number of systems to be decoupled is given by
operations acting sparsely to eliminate noise terms of range k. For instance, performing such an action on every second qubit eliminates all nearest neighbor two-qubit noise terms in a 1D setting (acting on every kth qubit eliminates confined k-body noise terms). However, this also eliminates the desired evolution for half of the particles (every kth particle), and these particles no longer contribute to the sensing process. As long as the number of systems to be decoupled is given by  with α being some constant—which is the case for any finite range k noise operators—we still obtain Heisenberg scaling
with α being some constant—which is the case for any finite range k noise operators—we still obtain Heisenberg scaling  .
.
Appendix C.: Parallel noise upper-bound QFI
In this section we derive a limitation on the maximally achievable QFI in presence of the parallel noise, i.e., noise that is described by the same generator as the Hamiltonian H that governs the evolution. Such parallel noise results in the channel

where λ is a random variable and  is a probability distribution with standard deviation σ characterizing the strength of the noise. As already mentioned such type of noise cannot be ameliorated using error correction as the operator generating it is identical to the Hamiltonian generating the desired evolution. The noise process in equation (C.1) can be viewed as describing classical noise applied directly on the estimated parameter ω, i.e., in every run of the experiment the observed parameter fluctuates by an amount λ, with λ being a random variable with corresponding probability distribution
is a probability distribution with standard deviation σ characterizing the strength of the noise. As already mentioned such type of noise cannot be ameliorated using error correction as the operator generating it is identical to the Hamiltonian generating the desired evolution. The noise process in equation (C.1) can be viewed as describing classical noise applied directly on the estimated parameter ω, i.e., in every run of the experiment the observed parameter fluctuates by an amount λ, with λ being a random variable with corresponding probability distribution  .
.
Recall that the QFI of a state ρ is given by [47]

where  and
and  is the Uhlmann fidelity. So one can access the QFI in the presence of parallel noise (equation (C.1)) through the Uhlmann fidelity
is the Uhlmann fidelity. So one can access the QFI in the presence of parallel noise (equation (C.1)) through the Uhlmann fidelity
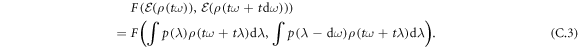
The Uhlmann fidelity is strongly concave

which implies that equation (C.3) is lower bounded by the fidelity of the probability distributions  and
and 


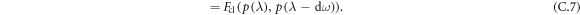
Consequently the QFI in the presence of parallel noise is bounded by the classical Fisher information of the probability distribution characterizing the noise
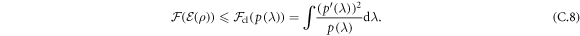
On the other hand we know than the QFI in the noisy case is lower that the noiseless QFI (attained by the GHZ state), therefore  . Combining the two bounds one gets for the QFI per unit time
. Combining the two bounds one gets for the QFI per unit time

It remains to find the time t that maximizes the rhs Trivially the maximum is attained when  , which yields
, which yields

For any smooth distribution  the classical Fisher information
the classical Fisher information  is finite, and therefore SQL scaling for the QFI per unit time is enforced. In particular for a Gaussian noise with
is finite, and therefore SQL scaling for the QFI per unit time is enforced. In particular for a Gaussian noise with  this bound implies
this bound implies
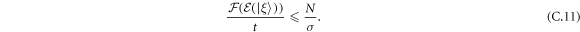
While for a simple strategy with GHZ states and the optimal choice of the time a straightforward calculation gives  , which is roughly half of the bound above.
, which is roughly half of the bound above.
Appendix D.: Two-qubit Hamiltonians and gate implementation
Consider the following Hamiltonian acting on two qubits plus an unspecified environment
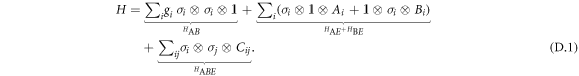
In the equation above the first term corresponds to the useful two-qubit interaction, the second term couples one of the qubits to the environment locally (though the environment can be global if e.g.  ), and the last term corresponds to non-local noise. Since we are interested in the implementation of two-qubit gates we consider a general dynamical decoupling sequence which only contains local pulse, i.e., unitaries that act on one of the qubits locally. Analogously to equation (3) a general sequence of this form modifies the Hamiltonian as
), and the last term corresponds to non-local noise. Since we are interested in the implementation of two-qubit gates we consider a general dynamical decoupling sequence which only contains local pulse, i.e., unitaries that act on one of the qubits locally. Analogously to equation (3) a general sequence of this form modifies the Hamiltonian as
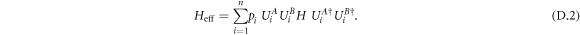
Note that in this context H is the most general two-qubit plus environment Hamiltonian, as the missing Hamiltonian of the environment  does not affect the capabilities of dynamical decoupling protocol, while local Hamiltonians of the qubits
does not affect the capabilities of dynamical decoupling protocol, while local Hamiltonians of the qubits  and
and  can be effectively removed by continually applying a field that compensates for their effect.
can be effectively removed by continually applying a field that compensates for their effect.
Just as before, our goal is to identify all the Hamiltonians H for which all the noise terms can be decoupled while keeping some part of the interaction between the qubits. If this is the case one can perform any two qubit gate in a noiseless fashion by tuning the interaction time, which allows for universal quantum computation. It has been shown in [32] that by applying a correlated depolarizing sequence of pulses all local noise terms  can be decoupled while keeping one interaction term, say
can be decoupled while keeping one interaction term, say  intact.
intact.
In fact dynamical decoupling also allows to deal with non-local noise terms. By applying the gates  with equal probability in equation (D.2) one cancels all the terms containing
with equal probability in equation (D.2) one cancels all the terms containing  in the Hamiltonian except
in the Hamiltonian except  . Obviously, by an adopted sequence one can also project out all the terms except a product of two Paulis in two arbitrary directions
. Obviously, by an adopted sequence one can also project out all the terms except a product of two Paulis in two arbitrary directions  , with
, with  and
and  . Consequently, such a strategy allows to recover a noiseless interaction iff there exist two vectors
. Consequently, such a strategy allows to recover a noiseless interaction iff there exist two vectors  and
and  such that
such that

while  . In other words, at least one of the environment operators in the locally rotated frame is zero
. In other words, at least one of the environment operators in the locally rotated frame is zero

where OA and OB are 3 × 3 orthogonal matrices. This means that noises up to rank 15 can in principle be corrected.
Footnotes
- 3
For this to hold one requires perfect knowledge of r3. This means perfect knowledge of the direction of the sensing Hamiltonian
 and perfect control of the decoupling pulses. This is a standard assumption in metrology.
and perfect control of the decoupling pulses. This is a standard assumption in metrology.




