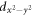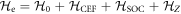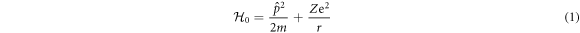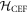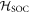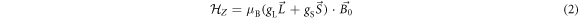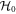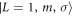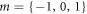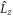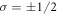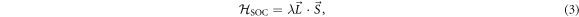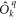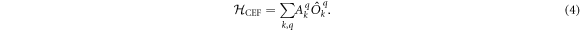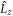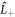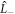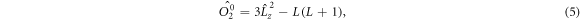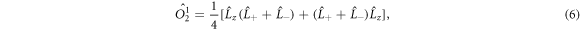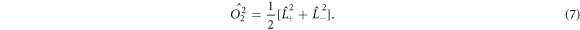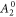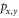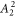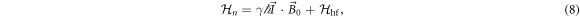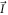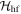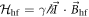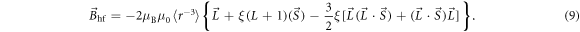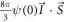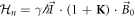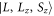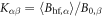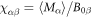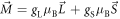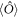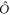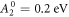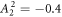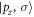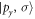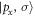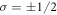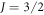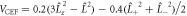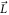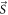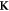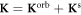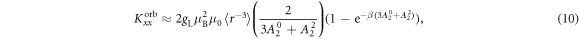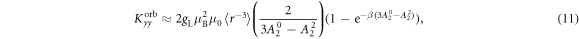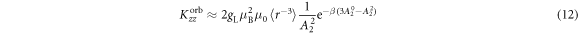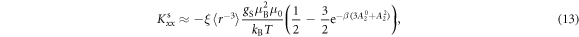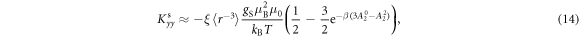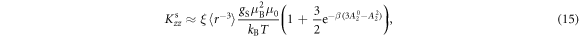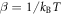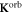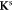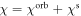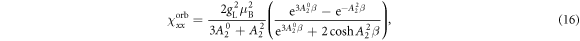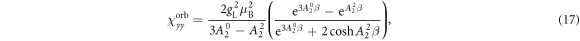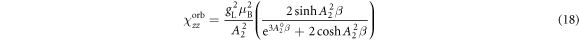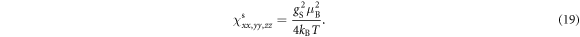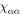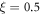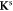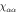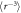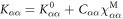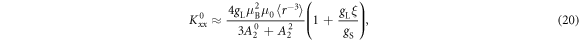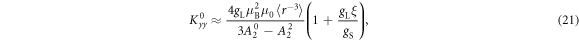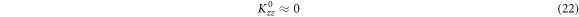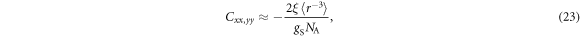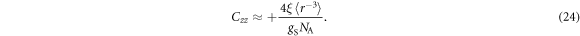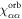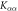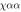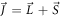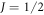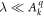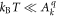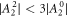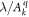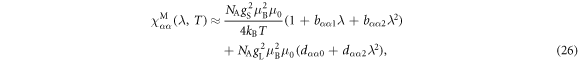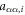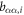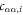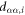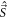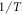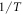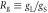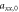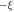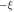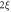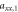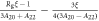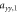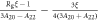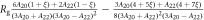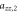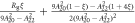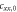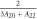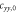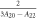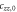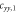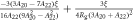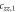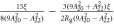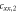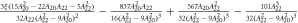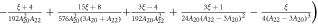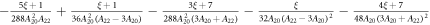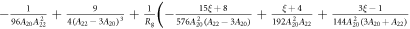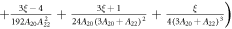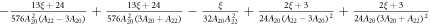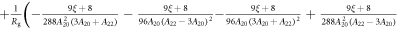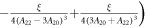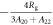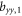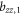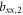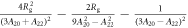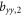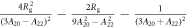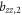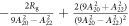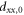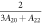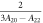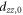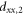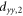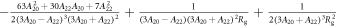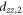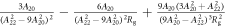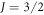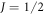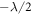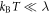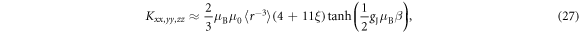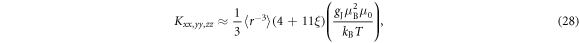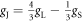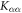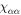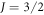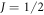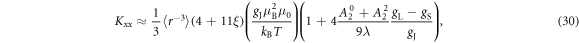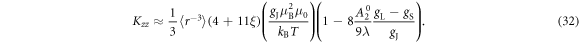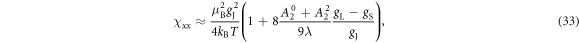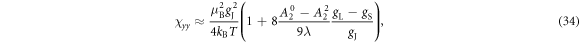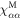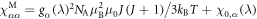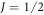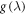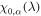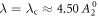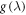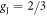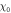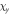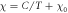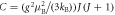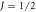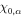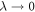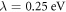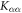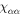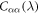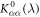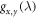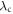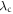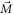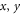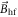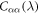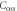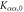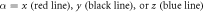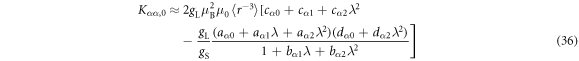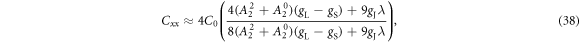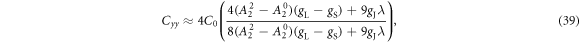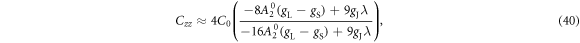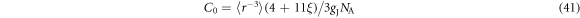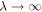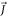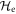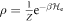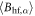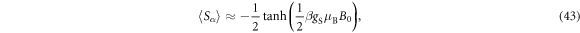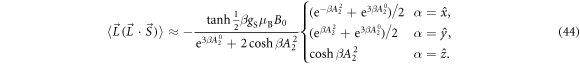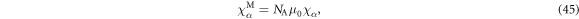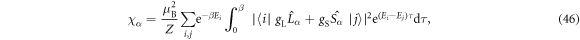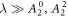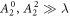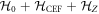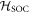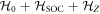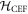Nuclear magnetic resonance Knight shifts in the presence of strong spin–orbit and crystal-field potentials

In recent years there has been considerable interest in the basic physics of strongly correlated electron materials with large spin–orbit interactions [1–3]. The spin–orbit interaction is responsible for many emergent phenomena in topological insulators and Weyl semi-metals, and is also of paramount importance in heavy fermion systems. Depending on the particular material, the spin–orbit coupling (SOC) can be roughly on the same scale as the crystalline electric field (CEF) interaction, but there are important differences. For the 3d electrons, the CEF interaction (∼eV) is typically much larger than the SOC (∼meV), whereas for 4f electrons, the converse is true [4, 5]. 4d and 5d systems typically lie between these two extremes, and the competition between these interactions can lead to novel phenomena [6].

Nuclear magnetic resonance (NMR) is an important technique that can shed light on the microscopic spin and charge degrees of freedom in these systems. The power of this technique lies in the hyperfine interaction between the nuclear spins and the electrons [7, 8]. Since the energy scale for the nuclear spin interactions are orders of magnitude smaller than the those for the electrons, perturbations of the nuclear spin system do not significantly affect the electrons. As a result the nuclei offer an unperturbed window onto the electronic system, however an understanding of the hyperfine coupling is vital to interpret the NMR response in any particular system. For example, in the cuprate high temperature superconductors, ⁶³Cu and ¹⁷O NMR have shed important light onto the dynamics of the electrons and on the nature of the superconducting state through the presence of on-site and transferred hyperfine interactions [9, 10]. In this system, the spin–orbit interaction is negligible, and the 3d orbitals of the Cu are split by a large CEF interaction. There is a single hole in the ${d}_{{x}^{2}-{y}^{2}}$ orbital of the Cu with a net spin moment. In an applied magnetic field, the orbital moment of this hole is partially unquenched, giving rise to a finite orbital susceptibility as well. These spin and orbital moments both contribute to the bulk magnetization of the material and to the hyperfine field experienced by the nuclear spins. In the paramagnetic state, the spin and orbital contributions to the Knight shift are known as the spin shift and the orbital shift² . The orbital shift, however, is temperature independent because it arises as a Van Vleck term from the excited states in this system. The temperature dependence of both the bulk susceptibility and the Knight shift arises solely from the spin moments. By measuring the Knight shift and the bulk susceptibility independently, and plotting the shift versus the susceptibility with temperature as an implicit parameter (a so-called Clogston–Jaccarino plot), one can extract the orbital contribution to the shift from the intercept and the hyperfine coupling from the slope of the line [11–13].

Distinguishing these two contributions is important because it enables one to discern the symmetry of the spin component of the superconducting wavefunction. If the condensate is a spin singlet, then the spin susceptibility should vanish as $T\to 0$. Since the bulk susceptibility of a superconductor is dominated by the large diamagnetic orbital contribution, it is not possible to measure the spin susceptibility from magnetization measurements. If there is a sufficiently large hyperfine coupling, however, the Knight shift is often dominated by the spin, rather than orbital, susceptibility. Therefore NMR Knight shift measurements in the superconducting state are usually the primary experimental method to discern the spin response of the condensate [14–16]. In order to properly measure the spin shift it is vital to first determine the orbital shift with sufficient precision to discern if any changes observed in the total Knight shift should be attributed to the spin component.

In materials with strong SOC the orbital and spin contributions to the magnetic susceptibility cannot be considered separately. In the context of the heavy fermions containing 4f or 5f electrons, both the Knight shift and the susceptibility are strongly temperature dependent [17]. In these systems, the Knight shift is linearly proportional to the bulk susceptibility at high temperatures, but often exhibits an anomaly at low temperatures, in which case the linear behavior breaks down. This has been attributed to the presence of a hyperfine coupling to two different spin degrees of freedom: the local 4f (5f) moments and the itinerant conduction electron spins [18]. The anomalous behavior emerges once these two types of spins become entangled below a characteristic coherence temperature, T^*. However, in the high temperature regime, the susceptibility is dominated by the 4f moments, which experience large SOCs. In this case both the orbital and spin susceptibility of the 4f moments are strongly temperature dependent, and the nuclear spins, which typically are located on ligand sites rather than the 4f site, experience an effective hyperfine coupling to the total spin, J, of the 4f moments. NMR studies typically are only concerned with and report this effective hyperfine coupling, given by the slope of the Clogston–Jaccarino plots. However, there is little microscopic knowledge about how these empirical numbers are related to the actual hyperfine couplings, nor is there any consensus over the significance of the intercepts in these plots.

In order to shed light on the roles of SOC and CEF interactions in the context of NMR Knight shifts, we have studied a simple model of a localized p-electron coupled to a nuclear spin. We investigate the behavior of the Clogston–Jaccarino plot as a function of the SOC, and find that both the effective hyperfine coupling (slope) and the intercept are strong functions of the SOC. For a critical value of the SOC relative to the CEF interaction some components of the susceptibility tensor vanish, whereas the Knight shift remains finite. As a result the effective hyperfine coupling becomes arbitrarily large. This anomalous behavior occurs because the spin and orbital contributions to susceptibility cancel, whereas the hyperfine fields due to the spin and orbital momenta of the electrons do not. As the SOC interaction increases, both the effective hyperfine coupling and the relative sizes of spin and orbital contributions become independent of the SOC. In section 2 we describe the model system, and in section 3 we discuss our calculations of how this model system behaves with varying strengths of the SOC.

We consider a model system of a localized electron in a p-orbital. For the electron, the Hamiltonian is given by ${{ \mathcal H }}_{{\rm{e}}}={{ \mathcal H }}_{0}+{{ \mathcal H }}_{\mathrm{CEF}}+{{ \mathcal H }}_{\mathrm{SOC}}+{{ \mathcal H }}_{Z}$, where

$$\begin{eqnarray}&&{{ \mathcal H }}_{0}=\displaystyle \frac{{\hat{p}}^{2}}{2m}+\displaystyle \frac{Z{{\rm{e}}}^{2}}{r}\end{eqnarray} \tag{ 1 }$$

is the atomic potential, ${{ \mathcal H }}_{\mathrm{CEF}}$ is the crystal field potential, ${{ \mathcal H }}_{\mathrm{SOC}}$ is the SOC, and

$$\begin{eqnarray}&&{{ \mathcal H }}_{Z}={\mu }_{{\rm{B}}}({g}_{{\rm{L}}}\vec{L}+{g}_{{\rm{S}}}\vec{S})\cdot \vec{{B}_{0}}\end{eqnarray} \tag{ 2 }$$

is the Zeeman interaction with an external magnetic field ${\vec{B}}_{0}$. We consider only the n = 2, L = 1 manifold of states (p-orbitals) of ${{ \mathcal H }}_{0}$ for simplicity. The Hilbert space we consider is therefore spanned by $| L=1,m,\sigma \rangle$, where $m=\{-1,0,1\}$ is the ${\hat{L}}_{z}$ quantum number, and $\sigma =\pm 1/2$ is the spin of the electron. The SOC is given by:

$$\begin{eqnarray}&&{{ \mathcal H }}_{\mathrm{SOC}}=\lambda \vec{L}\cdot \vec{S},\end{eqnarray} \tag{ 3 }$$

where λ is the SOC parameter. The CEF interaction can be expressed in terms of the Stevens equivalent operators, ${\hat{O}}_{k}^{q}$, for the polynomial crystal-field potential term as:

$$\begin{eqnarray}&&{{ \mathcal H }}_{\mathrm{CEF}}=\displaystyle \sum _{k,q}{A}_{k}^{q}{\hat{O}}_{k}^{q}.\end{eqnarray} \tag{ 4 }$$

The Stevens operators are given in terms of the orbital angular momentum operators ${\hat{L}}_{z}$, ${\hat{L}}_{+}$, and ${\hat{L}}_{-}$ [19]. For the L = 1 case we consider here, the Stevens operators that influence the electronic states are the k = 2 operators:

$$\begin{eqnarray}&&\hat{{O}_{2}^{0}}=3{\hat{L}}_{z}^{2}-L(L+1),\end{eqnarray} \tag{ 5 }$$

$$\begin{eqnarray}&&\hat{{O}_{2}^{1}}=\displaystyle \frac{1}{4}[{\hat{L}}_{z}({\hat{L}}_{+}+{\hat{L}}_{-})+({\hat{L}}_{+}+{\hat{L}}_{-}){\hat{L}}_{z}],\end{eqnarray} \tag{ 6 }$$

$$\begin{eqnarray}&&\hat{{O}_{2}^{2}}=\displaystyle \frac{1}{2}[{\hat{L}}_{+}^{2}+{\hat{L}}_{-}^{2}].\end{eqnarray} \tag{ 7 }$$

The parameters A_k^q are determined by the specific lattice. ${A}_{2}^{1}$ is nonzero only if the crystal lattice is triclinic. For simplicity we will consider only monoclinic or hexagonal crystals that have mirror planes forcing ${A}_{2}^{1}=0$. In such cases the eigenstates of the CEF are simply the p-orbitals. These states all have the property that angular momentum is quenched, $\langle \vec{L}\rangle =0$. Note that ${A}_{2}^{0}$ controls the splitting between the p_z and the ${p}_{x,y}$ orbitals, whereas ${A}_{2}^{2}$ controls the splitting between the p_x and p_y orbitals.

The nuclear spin Hamiltonian is given by:

$$\begin{eqnarray}&&{{ \mathcal H }}_{n}=\gamma {\hslash }\vec{I}\cdot {\vec{B}}_{0}+{{ \mathcal H }}_{\mathrm{hf}},\end{eqnarray} \tag{ 8 }$$

where γ is the gyromagnetic ratio, $\vec{I}$ is the nuclear spin, and ${{ \mathcal H }}_{\mathrm{hf}}$ is the hyperfine interaction. The latter can be expressed by ${{ \mathcal H }}_{\mathrm{hf}}=\gamma {\hslash }\vec{I}\cdot {\vec{B}}_{\mathrm{hf}}$, where the hyperfine field is given by:

$$\begin{eqnarray}&&{\vec{B}}_{\mathrm{hf}}=-2{\mu }_{{\rm{B}}}{\mu }_{0}\langle {r}^{-3}\rangle \left\{\vec{L}+\xi (L+1)(\vec{S})-\displaystyle \frac{3}{2}\xi [\vec{L}(\vec{L}\cdot \vec{S})+(\vec{L}\cdot \vec{S})\vec{L}]\right\}.\end{eqnarray} \tag{ 9 }$$

Here ξ is a parameter that quantifies the strength of the dipole–dipole coupling between the electron and nuclear spins [20]. Note that we do not include the Fermi contact interaction, $\tfrac{8\pi }{3}\psi (0)\vec{I}\cdot \vec{S}$, in the expression for the hyperfine interaction because the wavefunction vanishes at the nucleus for the p states we consider here. The effective Hamiltonian at the nucleus can be expressed as: ${{ \mathcal H }}_{n}=\gamma {\hslash }\vec{I}\cdot (1+{\bf{K}})\cdot {\vec{B}}_{0}$, where the Knight shift tensor, ${\bf{K}}$, relates the hyperfine field, ${\vec{B}}_{\mathrm{hf}}$, to the applied field. Experimentally, the Knight shift is the frequency shift of a nuclear resonance relative to a nucleus in vacuum. Note that we ignore the effects of ${{ \mathcal H }}_{\mathrm{hf}}$ on the electronic energy levels (Born–Oppenheimer approximation).

To compute the magnetic susceptibility and the Knight shift, the electronic Hamiltonian was diagonalized numerically in terms of the atomic states $| L,{L}_{z},{S}_{z}\rangle$ using the Mathematica software. The tensor elements ${K}_{\alpha \beta }=\langle {B}_{\mathrm{hf},\alpha }\rangle /{B}_{0,\beta }$ and ${\chi }_{\alpha \beta }=\langle {M}_{\alpha }\rangle /{B}_{0\beta }$ were then computed, where $\vec{M}={g}_{{\rm{L}}}{\mu }_{{\rm{B}}}\vec{L}+{g}_{{\rm{S}}}{\mu }_{{\rm{B}}}\vec{S}$ is the electronic magnetization, and $\langle \hat{O}\rangle$ is the thermal averaged value of the operator $\hat{O}$.

We discuss three regimes: one where SOC is a small perturbation to the CEF, one where SOC is the dominant component of the Hamiltonian and CEF is a small perturbation, and one where the effects of SOC and CEF are comparable. Figure 1 shows the evolution of the energy eigenvalues for L = 1 as a function of the SOC coupling, λ, using the CEF parameters ${A}_{2}^{0}=0.2\,{\rm{eV}}$ and ${A}_{2}^{2}=-0.4$ eV. For $\lambda =0$ the ground state is given by $| {p}_{z},\sigma \rangle$, the first excited state by $| {p}_{y},\sigma \rangle$, and the highest state by $| {p}_{x},\sigma \rangle$, where $\sigma =\pm 1/2$ is the spin quantum number. These states evolve with increasing λ, becoming admixtures of entangled spin and orbital degrees of freedom. For sufficiently large λ, the ground state corresponds to the $J=1/2$ manifold, and the excited states belong to the $J=3/2$ manifold.

Zoom In Zoom Out Reset image size

3.1. Knight shift with crystal field splitting and no SOC

As seen in equation (9), the shift results from a hyperfine interaction with both the orbital, $\vec{L}$, and spin, $\vec{S}$, degrees of freedom. In a crystal with no SOC, the electrons are distributed mainly in the CEF ground state. In this case the orbital angular momentum of all the states is quenched. When a magnetic field is present, the ground state wavefunction acquires a small net orbital momentum and the spin degeneracy is lifted. Since the Zeeman interaction is nearly always much smaller than the CEF splitting, the orbital susceptibility is small and temperature-independent (Van–Vleck), whereas the spin susceptibility exhibits an isotropic Curie response. In this case, the orbital and spin contributions to ${\bf{K}}$ can be separated because they have different temperature dependences.

As shown in the appendix, the Knight shift tensor can be written as the sum of orbital and spin parts: ${\bf{K}}={{\bf{K}}}^{\mathrm{orb}}+{{\bf{K}}}^{{\rm{s}}}$, where the orbital shift tensor is given by

$$\begin{eqnarray}&&{K}_{{xx}}^{\mathrm{orb}}\approx 2{g}_{{\rm{L}}}{\mu }_{{\rm{B}}}^{2}{\mu }_{0}\langle {r}^{-3}\rangle \left(\displaystyle \frac{2}{3{A}_{2}^{0}+{A}_{2}^{2}}\right)(1-{{\rm{e}}}^{-\beta (3{A}_{2}^{0}+{A}_{2}^{2})}),\end{eqnarray} \tag{ 10 }$$

$$\begin{eqnarray}&&{K}_{{yy}}^{\mathrm{orb}}\approx 2{g}_{{\rm{L}}}{\mu }_{{\rm{B}}}^{2}{\mu }_{0}\langle {r}^{-3}\rangle \left(\displaystyle \frac{2}{3{A}_{2}^{0}-{A}_{2}^{2}}\right)(1-{{\rm{e}}}^{-\beta (3{A}_{2}^{0}-{A}_{2}^{2})}),\end{eqnarray} \tag{ 11 }$$

$$\begin{eqnarray}&&{K}_{{zz}}^{\mathrm{orb}}\approx 2{g}_{{\rm{L}}}{\mu }_{{\rm{B}}}^{2}{\mu }_{0}\langle {r}^{-3}\rangle \displaystyle \frac{1}{{A}_{2}^{2}}{{\rm{e}}}^{-\beta (3{A}_{2}^{0}-{A}_{2}^{2})}\end{eqnarray} \tag{ 12 }$$

and the spin shift tensor is:

$$\begin{eqnarray}&&{K}_{{xx}}^{{\rm{s}}}\approx -\xi \langle {r}^{-3}\rangle \displaystyle \frac{{g}_{{\rm{S}}}{\mu }_{{\rm{B}}}^{2}{\mu }_{0}}{{k}_{{\rm{B}}}T}\left(\displaystyle \frac{1}{2}-\displaystyle \frac{3}{2}{{\rm{e}}}^{-\beta (3{A}_{2}^{0}+{A}_{2}^{2})}\right),\end{eqnarray} \tag{ 13 }$$

$$\begin{eqnarray}&&{K}_{{yy}}^{{\rm{s}}}\approx -\xi \langle {r}^{-3}\rangle \displaystyle \frac{{g}_{{\rm{S}}}{\mu }_{{\rm{B}}}^{2}{\mu }_{0}}{{k}_{{\rm{B}}}T}\left(\displaystyle \frac{1}{2}-\displaystyle \frac{3}{2}{{\rm{e}}}^{-\beta (3{A}_{2}^{0}-{A}_{2}^{2})}\right),\end{eqnarray} \tag{ 14 }$$

$$\begin{eqnarray}&&{K}_{{zz}}^{{\rm{s}}}\approx \xi \langle {r}^{-3}\rangle \displaystyle \frac{{g}_{{\rm{S}}}{\mu }_{{\rm{B}}}^{2}{\mu }_{0}}{{k}_{{\rm{B}}}T}\left(1+\displaystyle \frac{3}{2}{{\rm{e}}}^{-\beta (3{A}_{2}^{0}-{A}_{2}^{2})}\right),\end{eqnarray} \tag{ 15 }$$

where $\beta =1/{k}_{{\rm{B}}}T$. Note that both ${{\bf{K}}}^{\mathrm{orb}}$ and ${{\bf{K}}}^{{\rm{s}}}$ are anisotropic, reflecting the anisotropy of the electron wavefunctions.

Similarly, the magnetic susceptibility tensor can be decomposed into orbital and spin components, $\chi ={\chi }^{\mathrm{orb}}+{\chi }^{{\rm{s}}}$, where

$$\begin{eqnarray}&&{\chi }_{{xx}}^{\mathrm{orb}}=\displaystyle \frac{2{g}_{{\rm{L}}}^{2}{\mu }_{{\rm{B}}}^{2}}{3{A}_{2}^{0}+{A}_{2}^{2}}\left(\displaystyle \frac{{{\rm{e}}}^{3{A}_{2}^{0}\beta }-{{\rm{e}}}^{-{A}_{2}^{2}\beta }}{{{\rm{e}}}^{3{A}_{2}^{0}\beta }+2\cosh {A}_{2}^{2}\beta }\right),\end{eqnarray} \tag{ 16 }$$

$$\begin{eqnarray}&&{\chi }_{{yy}}^{\mathrm{orb}}=\displaystyle \frac{2{g}_{{\rm{L}}}^{2}{\mu }_{{\rm{B}}}^{2}}{3{A}_{2}^{0}-{A}_{2}^{2}}\left(\displaystyle \frac{{{\rm{e}}}^{3{A}_{2}^{0}\beta }-{{\rm{e}}}^{{A}_{2}^{2}\beta }}{{{\rm{e}}}^{3{A}_{2}^{0}\beta }+2\cosh {A}_{2}^{2}\beta }\right),\end{eqnarray} \tag{ 17 }$$

$$\begin{eqnarray}&&{\chi }_{{zz}}^{\mathrm{orb}}=\displaystyle \frac{{g}_{{\rm{L}}}^{2}{\mu }_{{\rm{B}}}^{2}}{{A}_{2}^{2}}\left(\displaystyle \frac{2\sinh {A}_{2}^{2}\beta }{{{\rm{e}}}^{3{A}_{2}^{0}\beta }+2\cosh {A}_{2}^{2}\beta }\right)\end{eqnarray} \tag{ 18 }$$

and

$$\begin{eqnarray}&&{\chi }_{{xx},{yy},{zz}}^{{\rm{s}}}=\displaystyle \frac{{g}_{{\rm{S}}}^{2}{\mu }_{{\rm{B}}}^{2}}{4{k}_{{\rm{B}}}T}.\end{eqnarray} \tag{ 19 }$$

The molar susceptibility is given by ${\chi }_{\alpha \alpha }^{{\rm{M}}}={N}_{{\rm{A}}}{\mu }_{0}{\chi }_{\alpha \alpha }$, where N_A is Avogadro's number.

Figure 2 show plots for ${\chi }_{\alpha \alpha }$ and ${K}_{\alpha \alpha }$ versus temperature in the limit $\lambda =0$ for $\xi =0.5$. The orbital susceptibility is temperature independent and anisotropic, whereas the spin susceptibility exhibits an isotropic Curie dependence. Note that even though ${\chi }_{\alpha \alpha }^{{\rm{s}}}$ is isotropic, ${{\bf{K}}}^{{\rm{s}}}$ is not. The reason for this difference is that the hyperfine coupling reflects the symmetry of the orbitals. For p orbitals, there is no Fermi contact term, which would be isotropic. The hyperfine field arises from the dipole interaction between the electron in the orbitals and the nucleus. Therefore ${{\bf{K}}}^{{\rm{s}}}$ has dipolar symmetry for $T\to 0$, but at finite temperatures the excited CEF states disrupt this axial asymmetry.

Zoom In Zoom Out Reset image size

In the low temperature limit the Knight shift is linearly proportional to the susceptibility, ${K}_{\alpha \alpha }={K}_{\alpha \alpha }^{0}+{C}_{\alpha \alpha }{\chi }_{\alpha \alpha }^{{\rm{M}}}$, where the intercepts are given by:

$$\begin{eqnarray}&&{K}_{{xx}}^{0}\approx \displaystyle \frac{4{g}_{{\rm{L}}}{\mu }_{{\rm{B}}}^{2}{\mu }_{0}\langle {r}^{-3}\rangle }{3{A}_{2}^{0}+{A}_{2}^{2}}\left(1+\displaystyle \frac{{g}_{{\rm{L}}}\xi }{{g}_{{\rm{S}}}}\right),\end{eqnarray} \tag{ 20 }$$

$$\begin{eqnarray}&&{K}_{{yy}}^{0}\approx \displaystyle \frac{4{g}_{{\rm{L}}}{\mu }_{{\rm{B}}}^{2}{\mu }_{0}\langle {r}^{-3}\rangle }{3{A}_{2}^{0}-{A}_{2}^{2}}\left(1+\displaystyle \frac{{g}_{{\rm{L}}}\xi }{{g}_{{\rm{S}}}}\right),\end{eqnarray} \tag{ 21 }$$

$$\begin{eqnarray}&&{K}_{{zz}}^{0}\approx 0\end{eqnarray} \tag{ 22 }$$

and the slopes are given by:

$$\begin{eqnarray}&&{C}_{{xx},{yy}}\approx -\displaystyle \frac{2\xi \langle {r}^{-3}\rangle }{{g}_{{\rm{S}}}{N}_{{\rm{A}}}},\end{eqnarray} \tag{ 23 }$$

$$\begin{eqnarray}&&{C}_{{zz}}\approx +\displaystyle \frac{4\xi \langle {r}^{-3}\rangle }{{g}_{{\rm{S}}}{N}_{{\rm{A}}}}.\end{eqnarray} \tag{ 24 }$$

Figure 3 shows plots of these equations for representative parameters, shown as thick black lines in the case $\lambda =0$. These equations offer a procedure to measure the magnitude of the hyperfine coupling and the CEF parameters by making independent measurements of the Knight shift and the molar susceptibility. By plotting the former as a function of the latter with temperature as an implicit parameter (a so-called Clogston–Jaccarino plot), one can usually observe linear behavior [21]. The slope of the line is proportional to ξ, which measures the strength of the dipole coupling between the electrons and the nucleus. The intercepts are proportional to the orbital susceptibility, ${\chi }_{\alpha \alpha }^{\mathrm{orb}}$, which measures the strength of the field created by the electron currents at the nuclear site. The anisotropy of the intercept is determined by the CEF parameters [15], and the ratio of the CEF parameters can be extracted from the ratio of the intercepts.

Zoom In Zoom Out Reset image size

3.2. Evolution of Knight shift with increasing SOC

We now turn to the case where $\lambda \ne 0$. The SOC partially unquenches the angular momentum, and also couples the electron spin to the orbital angular moment. Furthermore, the SOC preserves time-reversal-symmetry and thus the double degeneracy of the eigenstates, but degenerate eigenstates with opposite expectation values of spin now have opposite expectation values of orbital angular momentum. These changes to the eigenstates consequently have a profound effect on the behavior of the spin and orbital contributions to the Knight shift, and the Clogston–Jaccarino analysis will no longer distinguish the spin and orbital contributions. The following sections describe numerical calculations of how varying strengths of the SOC affect the eigenstates, the Knight shift, and the susceptibility, as well as perturbation theory in the limits of both weak and strong SOC relative to the CEF.

3.2.1. Numerical results

Although the CEF and SOC eigenstates can be described analytically, the Hamiltonian containing both CEF and SOC interactions does not have a general analytical solution. In the case where CEF and SOC are of the same order of magnitude, such as in Bi₂Se₃ [22], it is necessary to diagonalize the Hamiltonian numerically. Figure 2(a) shows the behavior of χ as λ increases. In this case the orbital angular momentum is no longer quenched, and the orbital susceptibility exhibits Curie behavior. Above a critical value of SOC the orbital contribution exceeds the spin contribution to susceptibility and the difference between them approaches a constant value. The total susceptibility becomes isotropic as λ grows arbitrarily large and the eigenstates approach the $\vec{J}=\vec{L}+\vec{S}$ eigenstates. Figure 2(b) reveals that the Knight shift changes dramatically as λ increases. ${\bf{K}}$ changes sign, becomes more isotropic and is independent of λ in the limit of $\lambda \gg \max \{{A}_{20},{A}_{22}\}$. This limiting behavior reflects the isotropic $J=1/2$ eigenstates. Thus the effect the SOC is to remove some of the shift anisotropy introduced by the crystal fields.

3.2.2. Low coupling limit

It is useful to consider the behavior in the low and high coupling limits using perturbation theory. We first consider the case where $\lambda \ll {A}_{k}^{q}$ and ${k}_{{\rm{B}}}T\ll {A}_{k}^{q}$, choosing coordinates so that $| {A}_{2}^{2}| \lt 3| {A}_{2}^{0}|$ (so that the exponential terms in equation (10) are negligible), and solve analytically to second order in $\lambda /{A}_{k}^{q}$. As shown in the appendix, we find

$$\begin{eqnarray}{K}_{\alpha \alpha }(\lambda ,T) & \approx & \displaystyle \frac{{g}_{{\rm{S}}}{\mu }_{{\rm{B}}}^{2}{\mu }_{0}}{2{k}_{{\rm{B}}}T}\langle {r}^{-3}\rangle ({a}_{\alpha \alpha 0}+{a}_{\alpha \alpha 1}\lambda +{a}_{\alpha \alpha 2}{\lambda }^{2})\\ & & +2{g}_{{\rm{L}}}{\mu }_{{\rm{B}}}^{2}{\mu }_{0}\langle {r}^{-3}\rangle ({c}_{\alpha \alpha 0}+{c}_{\alpha \alpha 1}\lambda +{c}_{\alpha \alpha 2}{\lambda }^{2}),\end{eqnarray} \tag{ 25 }$$

$$\begin{eqnarray}{\chi }_{\alpha \alpha }^{{\rm{M}}}(\lambda ,T) & \approx & \displaystyle \frac{{N}_{{\rm{A}}}{g}_{{\rm{S}}}^{2}{\mu }_{{\rm{B}}}^{2}{\mu }_{0}}{4{k}_{{\rm{B}}}T}(1+{b}_{\alpha \alpha 1}\lambda +{b}_{\alpha \alpha 2}{\lambda }^{2})\\ & & +{N}_{{\rm{A}}}{g}_{{\rm{L}}}^{2}{\mu }_{{\rm{B}}}^{2}{\mu }_{0}({d}_{\alpha \alpha 0}+{d}_{\alpha \alpha 2}{\lambda }^{2}),\end{eqnarray} \tag{ 26 }$$

where the coefficients ${a}_{\alpha \alpha ,i}$, ${b}_{\alpha \alpha ,i}$, ${c}_{\alpha \alpha ,i}$ and ${d}_{\alpha \alpha ,i}$ are given in table 1. As the main contribution to the susceptibility is from the diagonal matrix elements of the $\hat{\vec{L}}$ and $\hat{\vec{S}}$ operators, which necessarily lead to components proportional to $1/T$, the susceptibility will remain approximately proportional to $1/T$, so that the K versus χ plot remains linear despite orbital contributions to the slope of the line, as seen in figure 3.

Table 1.  Coefficients in equation (25) ${R}_{{\rm{g}}}\equiv {g}_{{\rm{L}}}/{g}_{{\rm{S}}}$.

Coefficient	Value
${a}_{{xx},0}$	$-\xi$
${a}_{{yy},0}$	$-\xi$
${a}_{{zz},0}$	$2\xi$
${a}_{{xx},1}$	$\tfrac{{R}_{{\rm{g}}}\xi -1}{3{A}_{20}+{A}_{22}}-\tfrac{3\xi }{4(3{A}_{20}-{A}_{22})}$
${a}_{{yy},1}$	$\tfrac{{R}_{{\rm{g}}}\xi -1}{3{A}_{20}-{A}_{22}}-\tfrac{3\xi }{4(3{A}_{20}+{A}_{22})}$
${a}_{{zz},1}$	$\tfrac{9{A}_{20}\xi }{2(9{A}_{20}^{2}-{A}_{22}^{2})}$
${a}_{{xx},2}$	${R}_{{\rm{g}}}\tfrac{6{A}_{20}(1+\xi )-2{A}_{22}(1-\xi )}{(3{A}_{20}-{A}_{22}){(3{A}_{20}+{A}_{22})}^{2}}-\tfrac{3{A}_{20}(4+5\xi )-{A}_{22}(4+7\xi )}{8{(3{A}_{20}-{A}_{22})}^{2}(3{A}_{20}+{A}_{22})}$
${a}_{{yy},2}$	${R}_{{\rm{g}}}\tfrac{6{A}_{20}(1+\xi )+2{A}_{22}(1-\xi )}{(3{A}_{20}+{A}_{22}){(3{A}_{20}-{A}_{22})}^{2}}-\tfrac{3{A}_{20}(4+5\xi )+{A}_{22}(4+7\xi )}{8{(3{A}_{20}+{A}_{22})}^{2}(3{A}_{20}-{A}_{22})}$
${a}_{{zz},2}$	$\tfrac{{R}_{{\rm{g}}}\xi }{9{A}_{20}^{2}-{A}_{22}^{2}}+\tfrac{9{A}_{20}^{2}(1-\xi )-{A}_{22}^{2}(1+4\xi )}{2{(9{A}_{20}^{2}-{A}_{22}^{2})}^{2}}$
${c}_{{xx},0}$	$\tfrac{2}{3{A}_{20}+{A}_{22}}$
${c}_{{yy},0}$	$\tfrac{2}{3{A}_{20}-{A}_{22}}$
${c}_{{zz},0}$	0
${c}_{{xx},1}$	$\tfrac{3(3{A}_{20}+7{A}_{22})\xi }{16{A}_{22}(9{A}_{20}^{2}-{A}_{22}^{2})}+\tfrac{3\xi }{4{R}_{{\rm{g}}}{(3{A}_{20}-{A}_{22})}^{2}}$
${c}_{{yy},1}$	$\tfrac{-3(3{A}_{20}-7{A}_{22})\xi }{16{A}_{22}(9{A}_{20}^{2}-{A}_{22}^{2})}+\tfrac{3\xi }{4{R}_{{\rm{g}}}{(3{A}_{20}+{A}_{22})}^{2}}$
${c}_{{zz},1}$	$\tfrac{15\xi }{8(9{A}_{20}^{2}-{A}_{22}^{2})}-\tfrac{3(9{A}_{20}^{2}+{A}_{22}^{2})\xi }{2{R}_{{\rm{g}}}(9{A}_{20}^{2}-{A}_{22}^{2})}$
${c}_{{xx},2}$	$\tfrac{3\xi (15{A}_{20}^{2}-22{A}_{20}{A}_{22}-5{A}_{22}^{2})}{32{A}_{22}{({A}_{22}^{2}-9{A}_{20}^{2})}^{2}}-\tfrac{837{A}_{20}^{2}{A}_{22}}{16{({A}_{22}^{2}-9{A}_{20}^{2})}^{3}}+\tfrac{567{A}_{20}{A}_{22}^{2}}{32{({A}_{22}^{2}-9{A}_{20}^{2})}^{3}}-\tfrac{101{A}_{22}^{3}}{32{({A}_{22}^{2}-9{A}_{20}^{2})}^{3}}$
	$+\tfrac{243{A}_{20}^{5}}{32{A}_{22}^{2}{({A}_{22}^{2}-9{A}_{20}^{2})}^{3}}-\tfrac{81{A}_{20}^{4}}{32{A}_{22}{({A}_{22}^{2}-9{A}_{20}^{2})}^{3}}-\tfrac{1323{A}_{20}^{3}}{16{(9{A}_{20}^{2}-{A}_{22}^{2})}^{3}}+\tfrac{1}{{R}_{{\rm{g}}}}\left(\tfrac{1-3\xi }{144{A}_{20}^{2}({A}_{22}-3{A}_{20})}\right.$
	$-\tfrac{\xi +4}{192{A}_{20}^{2}{A}_{22}}+\tfrac{15\xi +8}{576{A}_{20}^{2}(3{A}_{20}+{A}_{22})}\left.+\tfrac{3\xi -4}{192{A}_{20}{A}_{22}^{2}}+\tfrac{3\xi +1}{24{A}_{20}({A}_{22}-3{A}_{20}){}^{2}}-\tfrac{\xi }{4({A}_{22}-3{A}_{20}){}^{3}}\right)$
${c}_{{yy},2}$	$-\tfrac{5\xi +1}{288{A}_{20}^{2}{A}_{22}}+\tfrac{\xi +1}{36{A}_{20}^{2}({A}_{22}-3{A}_{20})}-\tfrac{3\xi +7}{288{A}_{20}^{2}(3{A}_{20}+{A}_{22})}-\tfrac{\xi }{32{A}_{20}({A}_{22}-3{A}_{20}){}^{2}}-\tfrac{4\xi +7}{48{A}_{20}(3{A}_{20}+{A}_{22}){}^{2}}$
	$-\tfrac{1}{96{A}_{20}{A}_{22}^{2}}+\tfrac{9}{4({A}_{22}-3{A}_{20}){}^{3}}+\tfrac{1}{{R}_{{\rm{g}}}}\left(-\tfrac{15\xi +8}{576{A}_{20}^{2}({A}_{22}-3{A}_{20})}+\tfrac{\xi +4}{192{A}_{20}^{2}{A}_{22}}+\tfrac{3\xi -1}{144{A}_{20}^{2}(3{A}_{20}+{A}_{22})}\right.$
	$\left.+\tfrac{3\xi -4}{192{A}_{20}{A}_{22}^{2}}+\tfrac{3\xi +1}{24{A}_{20}(3{A}_{20}+{A}_{22}){}^{2}}+\tfrac{\xi }{4(3{A}_{20}+{A}_{22}){}^{3}}\right)$
${c}_{{zz},2}$	$-\tfrac{13\xi +24}{576{A}_{20}^{2}({A}_{22}-3{A}_{20})}+\tfrac{13\xi +24}{576{A}_{20}^{2}(3{A}_{20}+{A}_{22})}-\tfrac{\xi }{32{A}_{20}{A}_{22}^{2}}+\tfrac{2\xi +3}{24{A}_{20}({A}_{22}-3{A}_{20}){}^{2}}+\tfrac{2\xi +3}{24{A}_{20}(3{A}_{20}+{A}_{22}){}^{2}}$
	$+\tfrac{1}{{R}_{{\rm{g}}}}\left(-\tfrac{9\xi +8}{288{A}_{20}^{2}(3{A}_{20}+{A}_{22})}-\tfrac{9\xi +8}{96{A}_{20}({A}_{22}-3{A}_{20}){}^{2}}\right.-\tfrac{9\xi +8}{96{A}_{20}(3{A}_{20}+{A}_{22}){}^{2}}+\tfrac{9\xi +8}{288{A}_{20}^{2}({A}_{22}-3{A}_{20})}$
	$-\tfrac{\xi }{4({A}_{22}-3{A}_{20}){}^{3}}\left.+\tfrac{\xi }{4(3{A}_{20}+{A}_{22}){}^{3}}\right)$
${b}_{{xx},1}$	$-\tfrac{4{R}_{{\rm{g}}}}{3{A}_{20}+{A}_{22}}$
${b}_{{yy},1}$	$-\tfrac{4{R}_{{\rm{g}}}}{3{A}_{20}-{A}_{22}}$
${b}_{{zz},1}$	0
${b}_{{xx},2}$	$\tfrac{4{R}_{{\rm{g}}}^{2}}{{(3{A}_{20}+{A}_{22})}^{2}}-\tfrac{2{R}_{{\rm{g}}}}{9{A}_{20}^{2}-{A}_{22}^{2}}-\tfrac{1}{{(3{A}_{20}-{A}_{22})}^{2}}$
${b}_{{yy},2}$	$\tfrac{4{R}_{{\rm{g}}}^{2}}{{(3{A}_{20}-{A}_{22})}^{2}}-\tfrac{2{R}_{{\rm{g}}}}{9{A}_{20}^{2}-{A}_{22}^{2}}-\tfrac{1}{{(3{A}_{20}+{A}_{22})}^{2}}$
${b}_{{zz},2}$	$-\tfrac{2{R}_{{\rm{g}}}}{9{A}_{20}^{2}-{A}_{22}^{2}}+\tfrac{2(9{A}_{20}^{2}+{A}_{22}^{2})}{{(9{A}_{20}^{2}-{A}_{22}^{2})}^{2}}$
${d}_{{xx},0}$	$\tfrac{2}{3{A}_{20}+{A}_{22}}$
${d}_{{yy},0}$	$\tfrac{2}{3{A}_{20}-{A}_{22}}$
${d}_{{zz},0}$	0
${d}_{{xx},2}$	$-\tfrac{63{A}_{20}^{2}-30{A}_{22}{A}_{20}+7{A}_{22}^{2}}{2({A}_{22}-3{A}_{20}){}^{2}(3{A}_{20}+{A}_{22}){}^{3}}+\tfrac{1}{({A}_{22}-3{A}_{20}){}^{2}(3{A}_{20}+{A}_{22}){R}_{{\rm{g}}}}+\tfrac{1}{2(3{A}_{20}-{A}_{22}){}^{3}{R}_{{\rm{g}}}^{2}}$
${d}_{{yy},2}$	$-\tfrac{63{A}_{20}^{2}+30{A}_{22}{A}_{20}+7{A}_{22}^{2}}{2(3{A}_{20}-{A}_{22}){}^{3}(3{A}_{20}+{A}_{22}){}^{2}}+\tfrac{1}{(3{A}_{20}-{A}_{22})(3{A}_{20}+{A}_{22}){}^{2}{R}_{{\rm{g}}}}+\tfrac{1}{2(3{A}_{20}+{A}_{22}){}^{3}{R}_{{\rm{g}}}^{2}}$
${d}_{{zz},2}$	$\tfrac{3{A}_{20}}{({A}_{22}^{2}-9{A}_{20}^{2}){}^{2}}-\tfrac{6{A}_{20}}{({A}_{22}^{2}-9{A}_{20}^{2}){}^{2}{R}_{{\rm{g}}}}+\tfrac{9{A}_{20}(3{A}_{20}^{2}+{A}_{22}^{2})}{(9{A}_{20}^{2}-{A}_{22}^{2}){}^{3}{R}_{{\rm{g}}}^{2}}$

3.2.3. High coupling limit

In the limit of large λ or vanishing CEF, the eigenstates approach those of the total angular momentum. The $J=3/2$ states are quadruply degenerate with energy eigenvalue $+\lambda /2$ while the $J=1/2$ states are doubly degenerate with eigenvalue $-\lambda /2$. In the limit ${k}_{{\rm{B}}}T\ll \lambda$, the electrons will be predominantly in the $J=1/2$ eigenstates and the shift and susceptibility can be described by:

$$\begin{eqnarray}&&{K}_{{xx},{yy},{zz}}\approx \displaystyle \frac{2}{3}{\mu }_{{\rm{B}}}{\mu }_{0}\langle {r}^{-3}\rangle (4+11\xi )\tanh \left(\displaystyle \frac{1}{2}{g}_{{\rm{J}}}{\mu }_{{\rm{B}}}\beta \right),\end{eqnarray} \tag{ 27 }$$

$$\begin{eqnarray}&&{K}_{{xx},{yy},{zz}}\approx \displaystyle \frac{1}{3}\langle {r}^{-3}\rangle (4+11\xi )\left(\displaystyle \frac{{g}_{{\rm{J}}}{\mu }_{{\rm{B}}}^{2}{\mu }_{0}}{{k}_{{\rm{B}}}T}\right),\end{eqnarray} \tag{ 28 }$$

$$\begin{eqnarray}&&{\chi }_{{xx},{yy},{zz}}\approx \displaystyle \frac{{\mu }_{{\rm{B}}}^{2}{g}_{{\rm{J}}}^{2}}{4{k}_{{\rm{B}}}T},\end{eqnarray} \tag{ 29 }$$

where ${g}_{{\rm{J}}}=\tfrac{4}{3}{g}_{{\rm{L}}}-\tfrac{1}{3}{g}_{{\rm{S}}}$. Note that ${K}_{\alpha \alpha }$ and ${\chi }_{\alpha \alpha }$ are isotropic and independent of λ, as evident in figures 2 and 3.

If the CEF is treated as a small perturbation to these eigenstates, then its effect is to partially lift the degeneracy of the $J=3/2$ states and mix them into the $J=1/2$ ground states. This perturbation introduces an anisotropy into the energy level splitting to first order in the CEF parameters. The Knight shift becomes:

$$\begin{eqnarray}&&{K}_{{xx}}\approx \displaystyle \frac{1}{3}\langle {r}^{-3}\rangle (4+11\xi )\left(\displaystyle \frac{{g}_{{\rm{J}}}{\mu }_{{\rm{B}}}^{2}{\mu }_{0}}{{k}_{{\rm{B}}}T}\right)\left(1+4\displaystyle \frac{{A}_{2}^{0}+{A}_{2}^{2}}{9\lambda }\displaystyle \frac{{g}_{{\rm{L}}}-{g}_{{\rm{S}}}}{{g}_{{\rm{J}}}}\right),\end{eqnarray} \tag{ 30 }$$

$$\begin{eqnarray}&&{K}_{{yy}}\approx \displaystyle \frac{1}{3}\langle {r}^{-3}\rangle (4+11\xi )\left(\displaystyle \frac{{g}_{{\rm{J}}}{\mu }_{{\rm{B}}}^{2}{\mu }_{0}}{{k}_{{\rm{B}}}T}\right)\left(1+4\displaystyle \frac{{A}_{2}^{0}-{A}_{2}^{2}}{9\lambda }\displaystyle \frac{{g}_{{\rm{L}}}-{g}_{{\rm{S}}}}{{g}_{{\rm{J}}}}\right),\end{eqnarray} \tag{ 31 }$$

$$\begin{eqnarray}&&{K}_{{zz}}\approx \displaystyle \frac{1}{3}\langle {r}^{-3}\rangle (4+11\xi )\left(\displaystyle \frac{{g}_{{\rm{J}}}{\mu }_{{\rm{B}}}^{2}{\mu }_{0}}{{k}_{{\rm{B}}}T}\right)\left(1-8\displaystyle \frac{{A}_{2}^{0}}{9\lambda }\displaystyle \frac{{g}_{{\rm{L}}}-{g}_{{\rm{S}}}}{{g}_{{\rm{J}}}}\right).\end{eqnarray} \tag{ 32 }$$

The susceptibility is also anisotropic:

$$\begin{eqnarray}&&{\chi }_{{xx}}\approx \displaystyle \frac{{\mu }_{{\rm{B}}}^{2}{g}_{{\rm{J}}}^{2}}{4{k}_{{\rm{B}}}T}\left(1+8\displaystyle \frac{{A}_{2}^{0}+{A}_{2}^{2}}{9\lambda }\displaystyle \frac{{g}_{{\rm{L}}}-{g}_{{\rm{S}}}}{{g}_{{\rm{J}}}}\right),\end{eqnarray} \tag{ 33 }$$

$$\begin{eqnarray}&&{\chi }_{{yy}}\approx \displaystyle \frac{{\mu }_{{\rm{B}}}^{2}{g}_{{\rm{J}}}^{2}}{4{k}_{{\rm{B}}}T}\left(1+8\displaystyle \frac{{A}_{2}^{0}-{A}_{2}^{2}}{9\lambda }\displaystyle \frac{{g}_{{\rm{L}}}-{g}_{{\rm{S}}}}{{g}_{{\rm{J}}}}\right),\end{eqnarray} \tag{ 34 }$$

$$\begin{eqnarray}&&{\chi }_{{zz}}\approx \displaystyle \frac{{\mu }_{{\rm{B}}}^{2}{g}_{{\rm{J}}}^{2}}{4{k}_{{\rm{B}}}T}\left(1-16\displaystyle \frac{{A}_{2}^{0}}{9\lambda }\displaystyle \frac{{g}_{{\rm{L}}}-{g}_{{\rm{S}}}}{{g}_{{\rm{J}}}}\right).\end{eqnarray} \tag{ 35 }$$

3.2.4. Effective g-factor

As seen in equations (26) and (33), as well as in figure 2(a), the susceptibility follows a Curie law as a function of temperature, but with an effective Curie constant that is a strong function of the CEF and SOC parameters. This behavior can be described by an effective g-factor. To characterize this behavior, we fit the numerical results for ${\chi }_{\alpha \alpha }^{{\rm{M}}}$ to the sum of a temperature independent component plus a Curie-term: ${\chi }_{\alpha \alpha }^{{\rm{M}}}={g}_{\alpha }{(\lambda )}^{2}{N}_{{\rm{A}}}{\mu }_{{\rm{B}}}^{2}{\mu }_{0}J(J+1)/3{k}_{{\rm{B}}}T+{\chi }_{0,\alpha }(\lambda )$, where $J=1/2$, and $g(\lambda )$ and ${\chi }_{0,\alpha }(\lambda )$ are shown in figure 4. g_x and g_y vanish due to the cancellation of the orbital and spin moments for $\lambda ={\lambda }_{{\rm{c}}}\approx 4.50\,{A}_{2}^{0}$. As λ increases further, the orbital momentum dominates and $g(\lambda )$ approaches ${g}_{{\rm{J}}}=2/3$ in all directions.

Zoom In Zoom Out Reset image size

The temperature-independent component, ${\chi }_{0,\alpha }$, is largest as $\lambda \to 0$ due to the Van Vleck contributions from the CEF excitations. As the λ increases, ${\chi }_{0,\alpha }$ is influenced by two competing factors. The SOC overcomes quenching of the orbital angular momentum, which can enhance the Van Vleck contribution from the excited states. However, the SOC ties the orbital degrees of freedom to those of the spin, so that the orbital susceptibility approaches Curie behavior. For the example system used here this temperature-independent component reaches a maximum on the order of $\lambda =0.25\,\mathrm{eV}$.

3.2.5. Relationship between Knight shift and susceptibility

We now turn to the relationship between the Knight shift and the susceptibility. Figure 3 shows ${K}_{\alpha \alpha }$ versus ${\chi }_{\alpha \alpha }$ for various values of λ. The slopes, ${C}_{\alpha \alpha }(\lambda )$, and intercepts, ${K}_{\alpha \alpha }^{0}(\lambda )$, of these plots change dramatically as a function of λ, as shown in figure 5, which is our central result. ${C}_{\alpha \alpha }$ diverges along the x–and y–directions, reflecting the fact that ${g}_{x,y}(\lambda )$ vanishes at ${\lambda }_{{\rm{c}}}$. This behavior does not reflect a change in the microscopic hyperfine coupling parameters, ξ or $\langle {r}^{-3}\rangle$, but rather the fact that the spin and orbital degrees of freedom are entangled. Near ${\lambda }_{{\rm{c}}}$, it is nearly impossible to induce a magnetization $\vec{M}$ in the $x,y$ plane because the spin and orbital moments cancel one another. However, it is possible to induce a significant hyperfine field, ${\vec{B}}_{\mathrm{hf}}$ because the spin shift arises due to the dipolar field from the electrons in the orbitals. As a result, the effective hyperfine coupling represented by the slope ${C}_{\alpha \alpha }(\lambda )$ can be much larger than the microscopic value.

Zoom In Zoom Out Reset image size

The values of the slopes and intercepts for $\lambda =0$ are given above in equations (20) and (23). In the limit of small λ, these intercepts and slopes are given by:

$$\begin{eqnarray}{K}_{\alpha \alpha ,0} & \approx & 2{g}_{{\rm{L}}}{\mu }_{{\rm{B}}}^{2}{\mu }_{0}\langle {r}^{-3}\rangle [{c}_{\alpha 0}+{c}_{\alpha 1}+{c}_{\alpha 2}{\lambda }^{2}\\ & & -\displaystyle \frac{{g}_{{\rm{L}}}}{{g}_{{\rm{S}}}}\left.\displaystyle \frac{({a}_{\alpha 0}+{a}_{\alpha 1}\lambda +{a}_{\alpha 2}{\lambda }^{2})({d}_{\alpha 0}+{d}_{\alpha 2}{\lambda }^{2})}{1+{b}_{\alpha 1}\lambda +{b}_{\alpha 2}{\lambda }^{2}}\right]\end{eqnarray} \tag{ 36 }$$

and

$$\begin{eqnarray}&&{C}_{\alpha \alpha }\approx \displaystyle \frac{2\langle {r}^{-3}\rangle }{{g}_{{\rm{S}}}{N}_{{\rm{A}}}}\left(\displaystyle \frac{{a}_{\alpha 0}+{a}_{\alpha 1}\lambda +{a}_{\alpha 2}{\lambda }^{2}}{1+{b}_{\alpha 1}\lambda +{b}_{\alpha 2}{\lambda }^{2}}\right),\end{eqnarray} \tag{ 37 }$$

where the coefficients are given in table 1. In the opposite limit at large λ, the intercepts are zero, and the slopes are given by:

$$\begin{eqnarray}&&{C}_{{xx}}\approx 4{C}_{0}\left(\displaystyle \frac{4({A}_{2}^{2}+{A}_{2}^{0})({g}_{{\rm{L}}}-{g}_{{\rm{S}}})+9{g}_{{\rm{J}}}\lambda }{8({A}_{2}^{2}+{A}_{2}^{0})({g}_{{\rm{L}}}-{g}_{{\rm{S}}})+9{g}_{{\rm{J}}}\lambda }\right),\end{eqnarray} \tag{ 38 }$$

$$\begin{eqnarray}&&{C}_{{yy}}\approx 4{C}_{0}\left(\displaystyle \frac{4({A}_{2}^{2}-{A}_{2}^{0})({g}_{{\rm{L}}}-{g}_{{\rm{S}}})+9{g}_{{\rm{J}}}\lambda }{8({A}_{2}^{2}-{A}_{2}^{0})({g}_{{\rm{L}}}-{g}_{{\rm{S}}})+9{g}_{{\rm{J}}}\lambda }\right),\end{eqnarray} \tag{ 39 }$$

$$\begin{eqnarray}&&{C}_{{zz}}\approx 4{C}_{0}\left(\displaystyle \frac{-8{A}_{2}^{0}({g}_{{\rm{L}}}-{g}_{{\rm{S}}})+9{g}_{{\rm{J}}}\lambda }{-16{A}_{2}^{0}({g}_{{\rm{L}}}-{g}_{{\rm{S}}})+9{g}_{{\rm{J}}}\lambda }\right),\end{eqnarray} \tag{ 40 }$$

where

$$\begin{eqnarray}&&{C}_{0}=\langle {r}^{-3}\rangle (4+11\xi )/3{g}_{{\rm{J}}}{N}_{{\rm{A}}}\end{eqnarray} \tag{ 41 }$$

is the limiting value as $\lambda \to \infty$.

The model system discussed here concerns the hyperfine field on-site at the nucleus of a single atom, and ignores the effects of hybridization with other orbitals in itinerant electron systems. As a result, the susceptibility and Knight shift exhibit Curie behavior, which clearly is not relevant for many solid state systems of interest. However, the general relationship between the Knight shift and the susceptibility does provide useful insight in to the effects of SOC and some broad conclusions can be drawn from these results. In cases where the SOC can be neglected, it is possible to separate the orbital and spin contributions to the susceptibility directly from the plots of Knight shift versus susceptibility [23, 24].On the other hand, when SOC become sufficiently large the slope and intercept of the Clogston–Jaccarino plot can change dramatically.In particular, the intercept is no longer simply related to the orbital susceptibility, nor is the slope a direct measure of the hyperfine parameter ξ. This result has important implications for the interpretation of the Knight shift in superconductors based on heavier elements, such as the iridates and heavy fermions.

Note that in many cases the nucleus observed by NMR is not the site containing the unpaired spin(s). In such cases the hyperfine coupling occurs via a transferred interaction, involving hybridization between the orbitals of the nucleus in question and the orbitals of nearby atoms (such as the Ce 4f) [10, 25]. The simple model case considered here does not include any such transferred interactions. Nevertheless, in heavy fermion materials with either 4f or 5f electrons the spin–orbit interaction is much larger than the crystal field interaction, in which case the Knight shift is dominated by the coupling to the total electron spin, $\vec{J}$. More detailed theoretical calculations considering the spin–orbit interaction in an itinerant hybridized system would be helpful to clarify the behavior of the NMR Knight shift in more detail.

In summary, we have considered a simple atomic model involving a hyperfine coupling to p electrons in the presence of SOC and crystal field interactions. We compute the Knight shift and magnetic susceptibility and find that these two quantities are linearly proportional to one another, however, the slope and intercept are complex functions of the spin–orbit and crystal field parameters. Under certain conditions the Knight shift response can far exceed the susceptibility, leading to a divergence in the slope of this ratio. This slope, however, is not a direct measure of the microscopic hyperfine coupling itself.

We thank the National Science Foundation under Grant No. DMR-1506961, and the Alfred H & Marie E Gibeling Fellowship at UC Davis for support for this work.

The thermal average hyperfine field (equation (9)) can be calculated by first computing the eigenvalues of the total Hamiltonian, ${{ \mathcal H }}_{{\rm{e}}}$, and then utilizing the thermal equilibrium density matrix $\rho =\tfrac{1}{Z}{{\rm{e}}}^{-\beta {{ \mathcal H }}_{{\rm{e}}}}$ to determine the expectation value of $\langle {B}_{\mathrm{hf},\alpha }\rangle$. The components are given by:

$$\begin{eqnarray}\langle {L}_{\alpha }\rangle \approx \displaystyle \frac{2{g}_{{\rm{L}}}{\mu }_{{\rm{B}}}{B}_{0}}{{{\rm{e}}}^{3\beta {A}_{2}^{0}}+2\cosh \beta {A}_{2}^{2}}\left\{\begin{array}{ll}\tfrac{{{\rm{e}}}^{-\beta {A}_{2}^{2}}-{{\rm{e}}}^{3\beta {A}_{2}^{0}}}{3{A}_{2}^{0}+{A}_{2}^{2}} & \alpha =\hat{x},\\ \tfrac{{{\rm{e}}}^{\beta {A}_{2}^{2}}-{{\rm{e}}}^{3\beta {A}_{2}^{0}}}{3{A}_{2}^{0}-{A}_{2}^{2}} & \alpha =\hat{y},\\ \displaystyle \frac{1}{{A}_{2}^{2}}\sinh \beta {A}_{2}^{2} & \alpha =\hat{z},\end{array}\right.\end{eqnarray} \tag{ 42 }$$

$$\begin{eqnarray}&&\langle {S}_{\alpha }\rangle \approx -\displaystyle \frac{1}{2}\tanh \left(\displaystyle \frac{1}{2}\beta {g}_{{\rm{S}}}{\mu }_{{\rm{B}}}{B}_{0}\right),\end{eqnarray} \tag{ 43 }$$

$$\begin{eqnarray}\langle \vec{L}(\vec{L}\cdot \vec{S})\rangle \approx -\displaystyle \frac{\tanh \tfrac{1}{2}\beta {g}_{{\rm{S}}}{\mu }_{{\rm{B}}}{B}_{0}}{{{\rm{e}}}^{3\beta {A}_{2}^{0}}+2\cosh \beta {A}_{2}^{2}}\left\{\begin{array}{ll}({{\rm{e}}}^{-\beta {A}_{2}^{2}}+{{\rm{e}}}^{3\beta {A}_{2}^{0}})/2 & \alpha =\hat{x},\\ ({{\rm{e}}}^{\beta {A}_{2}^{2}}+{{\rm{e}}}^{3\beta {A}_{2}^{0}})/2 & \alpha =\hat{y},\\ \cosh \beta {A}_{2}^{2} & \alpha =\hat{z}.\end{array}\right.\end{eqnarray} \tag{ 44 }$$

The components of the molar magnetic susceptibility tensor can be found as:

$$\begin{eqnarray}&&{\chi }_{\alpha }^{{\rm{M}}}={N}_{{\rm{A}}}{\mu }_{0}{\chi }_{\alpha },\end{eqnarray} \tag{ 45 }$$

$$\begin{eqnarray}&&{\chi }_{\alpha }=\displaystyle \frac{{\mu }_{{\rm{B}}}^{2}}{Z}\displaystyle \sum _{i,j}{{\rm{e}}}^{-\beta {E}_{i}}{\int }_{0}^{\beta }{| \langle i| {g}_{{\rm{L}}}{\hat{L}}_{\alpha }+{g}_{{\rm{S}}}\hat{{S}_{\alpha }}| j\rangle | }^{2}{{\rm{e}}}^{({E}_{i}-{E}_{j})\tau }{\rm{d}}\tau ,\end{eqnarray} \tag{ 46 }$$

where N_A is Avogadro's number.

A.1. Perturbation theory