U(1) Wilson lattice gauge theories in digital quantum simulators

We consider the Schwinger model, which describes the interaction between spinless fermions and antifermions, which will be referred to as electrons and positrons, via electric fields in one spatial dimension. In the following, we give an overview to this model in the continuum and on a lattice following the description in [45]. To this end, we introduce the vector potential at position x with temporal and spatial component ${\hat{A}}_{0}(x)$ and ${\hat{A}}_{1}(x)$. Throughout this paper, we use the temporal gauge ${\hat{A}}_{0}(x)=0$. In one spatial dimension, the electric field has only one component $\hat{E}(x)=-{\partial }_{0}{\hat{A}}_{1}(x)$, where ${\partial }_{0}$ is the partial derivative with respect to time. $\hat{E}(x)$ represents the canonical momentum conjugate to ${\hat{A}}_{1}(x)$ with $[{\hat{A}}_{1}(x),\hat{E}(x^{\prime} )]=-{\rm{i}}\delta (x-x^{\prime} )$. Matter fields are represented by two-component spinor fields ${\rm{\Psi }}(x)={({\hat{{\rm{\Psi }}}}_{{e}^{-}}(x),{\hat{{\rm{\Psi }}}}_{{e}^{+}}^{\dagger }(x))}^{T}$. The Schwinger Hamiltonian in the continuum is given by

$$\begin{eqnarray*}&&{\hat{H}}_{\mathrm{cont}}=\int {\rm{d}}{x}\left[-{\rm{i}}\bar{{\rm{\Psi }}}(x){\gamma }^{1}({\partial }_{1}+{\rm{i}}{g}{\hat{A}}_{1}(x)){\rm{\Psi }}(x)+m\bar{{\rm{\Psi }}}(x){\rm{\Psi }}(x)+\displaystyle \frac{1}{2}{\hat{E}}^{2}(x)\right],\end{eqnarray*}$$

where ${\partial }_{1}$ is the partial derivative with respect to x, m is the fermion mass and $\bar{{\rm{\Psi }}}\equiv {{\rm{\Psi }}}^{\dagger }{\gamma }^{0}$. In one spatial dimension, the Dirac matrices ${\gamma }^{0}$ and ${\gamma }^{1}$ are given by the Pauli operators ${\gamma }^{0}={\hat{\sigma }}^{z}$ and ${\gamma }^{1}={\rm{i}}{\hat{\sigma }}^{y}$. Using natural units ${\hslash }=c=1$, the coupling constant $g=-e$ is given by the charge e of the elementary particles. This model can be formulated on a lattice where points in space are separated by a distance a, while time is continuous. In the following, we are using the so-called Kogut–Susskind Hamiltonian formulation [29, 42, 55] of the lattice Schwinger model. In the compact U(1) lattice formulation we discuss here, the continuous fields ${\hat{A}}_{1}(x)$ and $\hat{E}(x)$ are replaced by a U(1) parallel transporter ${\hat{\theta }}_{n}=-{ag}{\hat{A}}_{1}({x}_{n})$ and its conjugate ${\hat{L}}_{n}=\tfrac{1}{g}\hat{E}({x}_{n})$. The operators ${\hat{L}}_{n}$, ${\hat{\theta }}_{n}$ are defined on the links connecting lattice sites n and $n+1$ as shown in figure 1(a) and commute canonically $[{\hat{\theta }}_{n},{\hat{L}}_{m}]={\rm{i}}{\delta }_{n,m}$. Particles are represented by Kogut–Susskind fermions, with one-component fermion field operators defined on each site n: ${\hat{{\rm{\Phi }}}}_{n}=\sqrt{a}{\hat{{\rm{\Psi }}}}_{{e}^{-}}({x}_{n})$ for even n and ${\hat{{\rm{\Phi }}}}_{n}=\sqrt{a}{\hat{{\rm{\Psi }}}}_{{e}^{+}}^{\dagger }({x}_{n})$ for odd n. The unit cell of this staggered lattice consists therefore of two sites and the presence of an electron (positron) is indicated by an occupied even (unoccupied odd) site, as sketched in figure 1(b). Accordingly, the interaction of matter- and gauge fields is described by the lattice Schwinger Hamiltonian

$$\begin{eqnarray}&&{\hat{{H}}}_{\mathrm{lat}}=-{\rm{i}}{w}\displaystyle \sum _{n=1}^{N-1}[{\hat{{\rm{\Phi }}}}_{n}^{\dagger }{{\rm{e}}}^{{\rm{i}}{\hat{\theta }}_{n}}{\hat{{\rm{\Phi }}}}_{n+1}-{\rm{H}}.{\rm{C}}.]+m\displaystyle \sum _{n=1}^{N}{(-1)}^{n}{\hat{{\rm{\Phi }}}}_{n}^{\dagger }{\hat{{\rm{\Phi }}}}_{n}+J\displaystyle \sum _{n=1}^{N-1}{\hat{L}}_{n}^{2},\end{eqnarray} \tag{ 1 }$$

where N is the number of lattice sites and m is the fermion mass; $w=\tfrac{1}{2a}$ and $J=\tfrac{{g}^{2}a}{2}$, where a is the lattice constant and g the fermion-light coupling constant. Using natural units ${\hslash }=c=1$, the parameters w, J, m, and g have the dimension of inverse length, while a and t (time) have the dimension of length. The first term in equation (1) describes nearest-neighbour hopping and corresponds to the creation and annihilation of electron–positron pairs⁸ . The second and the third term represent the rest mass and the electric field energy stored in the system, respectively. The resulting dynamics is constrained by the Gauss law⁹ . In the considered lattice formulation, it takes the form of a set of local constraints as illustrated in figures 1(b), (c). More precisely, physical states are eigenstates of the generators of the Gauss law ${\hat{G}}_{n}={\hat{L}}_{n}-{\hat{L}}_{n-1}-{\hat{{\rm{\Phi }}}}_{n}^{\dagger }{\hat{{\rm{\Phi }}}}_{n}+\tfrac{1}{2}[1-{(-1)}^{n}]$. We will be interested in the zero-charge subspace, where ${\hat{G}}_{n}| {\psi }_{\text{}{\rm{physical}}}\rangle =0$. Note that the electric field operators for each link take integer eigenvalues ${L}_{n}=0,\pm 1,\pm 2,\,\ldots$ .

In the following, we consider open boundary conditions and aim at realizing the Schwinger model in a spin system. This can be achieved by two transformations (see [1], Methods section). First, the fermionic field operators ${\hat{{\rm{\Phi }}}}_{n}$ can be mapped to Pauli spin operators by a Jordan–Wigner transformation [56],

$$\begin{eqnarray*}&&{\hat{{\rm{\Phi }}}}_{n}=\displaystyle \prod _{l\lt n}[{\rm{i}}{\hat{\sigma }}_{l}^{z}]{\hat{\sigma }}_{n}^{-}.\end{eqnarray*}$$

Second, the operators ${\hat{\theta }}_{n}$ can be eliminated by a gauge transformation [45],

$$\begin{eqnarray*}&&{\hat{\sigma }}_{n}^{-}\to \left[\displaystyle \prod _{l\lt n}{{\rm{e}}}^{-{\rm{i}}{\hat{\theta }}_{l}}\right]{\hat{\sigma }}_{n}^{-},\end{eqnarray*}$$

where each spin operator ${\hat{\sigma }}_{n}^{-}$ is multiplied by a phase that depends on all gauge field operators ${\hat{\theta }}_{l}$ to its left ($l\lt n$). In this way, the Schwinger model can be expressed in terms of spin operators ${\hat{\sigma }}_{n}$ representing the matter fields and electric field operators ${\hat{L}}_{n}$,

$$\begin{eqnarray*}&&{\hat{H^{\prime} }}_{\mathrm{lat}}=w\displaystyle \sum _{n=1}^{N-1}[{\hat{\sigma }}_{n}^{+}{\hat{\sigma }}_{n+1}^{-}+{\rm{H}}{\rm{.}}{\rm{C}}.]+\displaystyle \frac{m}{2}\displaystyle \sum _{n=1}^{N}{(-1)}^{n}{\hat{\sigma }}_{n}^{z}+J\displaystyle \sum _{n=1}^{N-1}{\hat{L}}_{n}^{2},\end{eqnarray*}$$

as shown in figure 1(c) (lower panel). In this formulation, the Gauss law takes the form ${\hat{L}}_{n}-{\hat{L}}_{n-1}=\tfrac{1}{2}[{\hat{\sigma }}_{n}^{z}+{(-1)}^{n}]$. As illustrated in figure 1(c), the electric fields are in the considered case of open boundary conditions completely determined for given choice of background field ${\epsilon }_{0}$ and for a given spin configuration that represents a certain fermion configuration. More specifically, the Gauss law allows one to express the electric field operators in the form ${\hat{L}}_{n}={\epsilon }_{0}+\tfrac{1}{2}{\sum }_{l=1}^{n}({\hat{\sigma }}_{l}^{z}+{(-1)}^{l})$, such that the gauge fields do no longer appear explicitly in the description [45]. Instead, the electric field energy term ${\hat{H}}_{\mathrm{lat}}^{E}=J{\sum }_{n=1}^{N-1}{\hat{L}}_{n}^{2}\,=J{\sum }_{n=1}^{N-1}{\left[{\epsilon }_{0}+\tfrac{1}{2}{\sum }_{l=1}^{n}({\hat{\sigma }}_{l}^{z}+{(-1)}^{l})\right]}^{2}$ gives rise to (i) a long-range spin–spin interaction ${\hat{H}}_{{ZZ}}$ that corresponds to the Coulomb interaction between the charged particles and (ii) local energy offsets that lead to modified effective fermion masses. For simplicity, we will assume a zero background field (the following results can be straightforwardly generalized to arbitrary background fields ${\epsilon }_{0}\ne 0$, which lead to local terms modifying the fermion on-site energies). The resulting Hamiltonian can be cast in the form ${\hat{H}}_{{\rm{S}}}={\hat{H}}_{{ZZ}}+{\hat{H}}_{\pm }+{\hat{H}}_{Z}$, with

$$\begin{eqnarray}&&{\hat{H}}_{{ZZ}}=\displaystyle \frac{J}{2}\displaystyle \sum _{n=1}^{N-2}\displaystyle \sum _{l=n+1}^{N-1}(N-l){\hat{\sigma }}_{n}^{z}{\hat{\sigma }}_{l}^{z},\end{eqnarray} \tag{ 2 }$$

$$\begin{eqnarray}&&{\hat{H}}_{\pm }=w\displaystyle \sum _{n=1}^{N-1}[{\hat{\sigma }}_{n}^{+}{\hat{\sigma }}_{n+1}^{-}+{\rm{H}}{\rm{.}}{\rm{C}}.],\end{eqnarray} \tag{ 3 }$$

$$\begin{eqnarray}&&{\hat{H}}_{Z}=\displaystyle \frac{m}{2}\displaystyle \sum _{n=1}^{N}{(-1)}^{n}{\hat{\sigma }}_{n}^{z}-\displaystyle \frac{J}{4}\displaystyle \sum _{n=1}^{N-1}[1-{(-1)}^{n}]\displaystyle \sum _{l=1}^{n}{\hat{\sigma }}_{l}^{z}.\end{eqnarray} \tag{ 4 }$$

As outlined in the introduction, the main challenge for realizing the Schwinger model in its encoded form in an actual physical system is the implementation of the long-range interaction Hamiltonian ${\hat{H}}_{{ZZ}}$, which features an exotic asymmetric distance dependence (see figure 2). Note that we could have encoded the electric field operators in the form ${\hat{L}}_{n}={\epsilon }_{0}-\tfrac{1}{2}{\sum }_{l=n+1}^{N}({\hat{\sigma }}_{l}^{z}+{(-1)}^{l})$. This alternative encoding results in a long-range spin–spin coupling of the same type, but with reverse directionality (i.e. every spin interacts with a constant strength with all spins to its right and the coupling to spins on its left decreases linearly with distance). Both descriptions are equally valid. If closed boundary conditions are used instead of the open ones considered here, it is not possible to eliminate all gauge fields. In this case, a free gauge degree of freedom remains which accounts for the dynamical flux in the loop.

In the following, we describe a protocol that allows one to simulate the lattice Schwinger model in a 1D spin system with long-range interactions. The protocol consists of a digital quantum simulation scheme where we incorporated ideas put forward in [57]. Due to the complicated form of the Hamiltonian ${\hat{H}}_{{ZZ}}$ given in equation (2), a standard digital simulation approach would require N² time steps, where N is the number of spins. In our protocol, the total number of time steps scales linearly with N and the realization of ${\hat{H}}_{{ZZ}}$ costs only $N-2$ time steps, which is optimal¹⁰ . Our approach is quite general, and requires only single qubit operations that can be applied to individual spins and one type of two-body interactions, ${\hat{H}}_{0}={J}_{0}{\sum }_{n,l}{\hat{\sigma }}_{n}^{a}{\hat{\sigma }}_{l}^{a}$, where a can correspond to any direction on the Bloch sphere and J₀ is the coupling strength. In the following, we will explain the protocol for $\hat{{H}_{0}}={J}_{0}{\sum }_{n,l}{\hat{\sigma }}_{n}^{x}\,{\hat{\sigma }}_{l}^{x}$. Adapting the scheme to $a\ne x$ requires only minor and straightforward modifications.

The quantum simulation protocol is based on a time-coarse graining, where the effective interaction given by equations (2)–(4) is obtained in a time-averaged description, while maintaining local gauge invariance at any stage. As illustrated in figure 3(a), the total simulation time ${t}_{\mathrm{sim}}$ is divided into several time windows of duration T, in the spirit of the Trotter decomposition [28, 58]. During each of these time windows, a full cycle of the protocol that is described below is performed. Each cycle consists of three sections as shown in figure 3(b). In sections 1 and 2, ${\hat{H}}_{{ZZ}}$ and ${\hat{H}}_{\pm }$ are simulated employing the spin–spin coupling ${\hat{H}}_{0}$. In section 3, only single particle rotations are performed realizing ${\hat{H}}_{Z}$.

Zoom In Zoom Out Reset image size

Section 1 is divided into $N-2$ smaller time windows of length ${\rm{\Delta }}{t}_{I}$ as shown in figure 3(c). For each of the $N-2$ time windows, a subgroup of spins is decoupled from the interaction, while the remaining spins interact according to ${\hat{H}}_{0}$. In the ${n}^{}{\rm{t}}{\rm{h}}$ time window of section 1, ions 1 to $n+1$ participate in the interaction, such that the Hamiltonian ${\hat{H}}_{0}^{(n+1)}={J}_{0}{\sum }_{k,l=1}^{n+1}{\hat{\sigma }}_{k}^{x}{\hat{\sigma }}_{l}^{x}$ is implemented. Since the realization of equation (2) requires ${\hat{\sigma }}_{k}^{z}{\hat{\sigma }}_{l}^{z}$-couplings, local single-particle rotations are added in the beginning and the end of section 1, rotating the x spin component into the z direction. The resulting time-evolution operator for section 1,

$$\begin{eqnarray}&&{{\rm{e}}}^{{\rm{i}}\tfrac{\pi }{4}{\sum }_{j}{\hat{\sigma }}_{j}^{y}}\left(\underset{m=2}{\overset{N-1}{\displaystyle \bigotimes }}{{\rm{e}}}^{-{\rm{i}}{\hat{H}}_{0}^{(m)}{\rm{\Delta }}{t}_{I}}\right){{\rm{e}}}^{-{\rm{i}}\tfrac{\pi }{4}{\sum }_{j}{\hat{\sigma }}_{j}^{y}}={{\rm{e}}}^{-{\rm{i}}{\hat{H}}_{{ZZ}}T},\end{eqnarray} \tag{ 5 }$$

realizes the desired ${\hat{H}}_{{ZZ}}$ for one time step T, with strength $J=2\tfrac{{\rm{\Delta }}{t}_{I}}{T}{J}_{0}$. For a single time step, this is exact. Trotter errors will be discussed in section 4.2, where we address imperfections of the scheme.

In section 2, the part of the Schwinger Hamiltonian involving nearest-neighbour interactions ${\hat{H}}_{\pm }$ is realized. To this end, the underlying interaction ${\hat{H}}_{0}$, needs to be modified not only in range but also regarding the type of couplings. This is accomplished by dividing section 2 into $N-1$ elementary time slots of length ${\rm{\Delta }}{t}_{{II}}$ (see figure 3(d)). Each of these time slots is used for inducing the required type of interaction between a specific pair of neighbouring atoms. This can be done by decoupling all but the selected pair of atoms from the evolution under ${\hat{H}}_{0}$. The selected pair of atoms undergoes a sequence of gate operations that transforms the ${\hat{\sigma }}_{n}^{x}{\hat{\sigma }}_{l}^{x}$-coupling into a $({\hat{\sigma }}_{n}^{+}{\hat{\sigma }}_{l}^{-}+{\hat{\sigma }}_{n}^{-}{\hat{\sigma }}_{l}^{+})$-interaction and consists of four steps (see figure 3(e)): (i) a single qubit operation on the two selected spins n and $n+1$, $U={{\rm{e}}}^{{\rm{i}}\tfrac{\pi }{4}({\hat{\sigma }}_{n}^{z}+{\hat{\sigma }}_{n+1}^{z})}$ (ii) an evolution of the qubits n and $n+1$ under the Hamiltonian ${\hat{H}}_{0}$ during a time ${\rm{\Delta }}{t}_{{II}}/2$, ${{\rm{e}}}^{-{\rm{i}}{\hat{H}}_{0}{\rm{\Delta }}{t}_{{II}}/2}$ (iii) another single qubit operation ${U}^{\dagger }$ and finally (iv) another two qubit gate operation ${{\rm{e}}}^{-{\rm{i}}{\hat{H}}_{0}{\rm{\Delta }}{t}_{{II}}/2}$. These four steps result in a time evolution with

$$\begin{eqnarray*}&&{{\rm{e}}}^{-{\rm{i}}{\hat{H}}_{0}\tfrac{{\rm{\Delta }}{t}_{{II}}}{2}}\cdot {U}^{\dagger }\cdot {{\rm{e}}}^{-{\rm{i}}{\hat{H}}_{0}\tfrac{{\rm{\Delta }}{t}_{{II}}}{2}}\cdot U={{\rm{e}}}^{-{\rm{i}}({\hat{H}}_{0}+{U}^{\dagger }{\hat{H}}_{0}U)\tfrac{{\rm{\Delta }}{t}_{{II}}}{2}}.\end{eqnarray*}$$

Note that this equation is exact. The time evolution operator associated with the described sequence of gate operations is given by ${{\rm{e}}}^{-{\rm{i}}{\hat{H}}_{{II}}^{(n,n+1)}{\rm{\Delta }}{t}_{{II}}}$ with

$$\begin{eqnarray*}&&{\hat{H}}_{{II}}^{(n,n+1)}=\displaystyle \frac{1}{2}({\hat{H}}_{0}+{U}^{\dagger }{\hat{H}}_{0}U)={J}_{0}({\hat{\sigma }}_{n}^{+}{\hat{\sigma }}_{n+1}^{-}+{\rm{H}}{\rm{.}}{\rm{C}}.).\end{eqnarray*}$$

Repeating these four steps for sites $n=1...N-1$ yields, as long as ${J}_{0}{\rm{\Delta }}{t}_{{II}}(N-1)\ll 1$ (see section 4.2), the desired evolution operator ${\hat{H}}_{{II}}={\sum }_{n=1}^{N-1}{\hat{H}}_{{II}}^{(n,n+1)}={\hat{H}}_{\pm }$, with $w=\tfrac{{\rm{\Delta }}{t}_{{II}}}{T}{J}_{0}$. The relative strength of the nearest-neighbour Hamiltonian ${\hat{H}}_{\pm }$ and the ${\hat{\sigma }}_{n}^{z}{\hat{\sigma }}_{l}^{z}$-type couplings ${\hat{H}}_{{ZZ}}$ can be adjusted by tuning the ratio of the elementary time windows ${\rm{\Delta }}{t}_{{II}}/{\rm{\Delta }}{t}_{I}$.

In section 3, the single qubit terms of the type ${\hat{H}}_{z}$ given in equation (4) are implemented. This Hamiltonian is realized in a single time window of length ${\rm{\Delta }}{t}_{{III}}$. All spins are acted upon simultaneously, but each one experiences a different coupling strength. Since we assume that single qubit operations can be performed on much faster time scales than gates operating on multiple spins, we use ${\rm{\Delta }}{t}_{{III}}\ll {\rm{\Delta }}{t}_{{II}},{\rm{\Delta }}{t}_{I}$. Together, the operations in the time sections 1, 2 and 3 approximately realize the time-evolution operator of the Schwinger model for one time step, ${{\rm{e}}}^{-{\rm{i}}{\hat{H}}_{{\rm{S}}}T}$. Trotter errors due to the finite-time coarse-graining will be discussed below in section 4, where we address imperfections of the scheme.

Since vacuum fluctuations promote the creation of particle–antiparticle pairs, the bare vacuum $| \mathrm{vac}\rangle$ (i.e. the state where particles are absent) is unstable. The particle number density $\nu (t)$ created out of the bare vacuum is measured by the observable

$$\begin{eqnarray*}&&\nu (t)=\displaystyle \frac{1}{N}\displaystyle \sum _{n=1}^{N}\langle {(-1)}^{n}{\hat{{\rm{\Phi }}}}_{n}^{\dagger }(t){\hat{{\rm{\Phi }}}}_{n}(t)\rangle \,\end{eqnarray*}$$

with $\langle ...\rangle =\langle \mathrm{vac}| \,...\,| \mathrm{vac}\rangle$ denoting the average with respect to the initial vacuum state. After transforming the fermonic fields to spin operators by a Jordan–Wigner transformation (see section 2.1), the particle number density is given by $\nu (t)=\tfrac{1}{2N}{\sum }_{n=1}^{N}\langle {(-1)}^{n}{\hat{\sigma }}_{n}^{z}(t)+1\rangle$ and can be determined through local magnetization measurements (see figure 4(a)). In figure 4(b), the quantum real-time dynamics of $\nu (t)$ is shown, illustrating the instability of the vacuum. Initially, particles are produced quickly. After a sufficiently large particle density has been generated, particle–antiparticle recombination becomes favoured, inducing a decrease of $\nu (t)$. This nonequilibrium interplay of regimes with either dominating production or recombination continues over time, leading to an oscillatory behaviour of $\nu (t)$ with a slowly decaying envelope. Asymptotically, the system reaches a steady state with a balance between particle production and recombination. As shown in figure 4(a), increasing particle masses lead to a decrease in the particle production because of the increasing energy costs for pair creation. Similarly, with larger values of J/w, the higher cost of generating a field string between electrons and positrons reduces the density of generated pairs, see figure 5.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

An important quantity in the context of dynamics in the Schwinger model is the vacuum persistence amplitude [30]

$$\begin{eqnarray*}&&{ \mathcal G }(t)=\langle \mathrm{vac}| {{\rm{e}}}^{-{\rm{i}}{\hat{H}}_{{\rm{S}}}t}| \mathrm{vac}\rangle ,\end{eqnarray*}$$

which measures the deviation from the initial state during the simulated dynamics and quantifies therefore the aforementioned decay of the unstable vacuum. In the continuum limit it has been shown that the decay of the vacuum is directly related to the particle production $\nu (t)=\lambda (t)$ with $\lambda (t)=-{N}^{-1}\mathrm{log}(| { \mathcal G }(t){| }^{2})$ [30]. In figure 5, we show a comparison between $\lambda (t)$ and $\nu (t)$ for different parameters. While on the lattice their one-to-one relation $\nu (t)=\lambda (t)$ is broken, we find numerically that the similarity between $\lambda (t)$ and $\nu (t)$ nevertheless remains clearly visible. Vacuum persistence amplitudes are not only important for spontaneous pair creation. They appear under different names in a variety of contexts in quantum many-body theory and are therefore also of interest in other types of quantum simulations (for example, in the theory of quantum chaos [62] the associated probability ${ \mathcal L }(t)=| { \mathcal G }(t){| }^{2}$ is also known as the Loschmidt echo and quantifies the stability of quantum motion [63]). It plays also a central role in dynamical quantum phase transitions far from equilibrium [64, 65]. In quantum thermodynamics, the Fourier transform of ${ \mathcal G }(t)$ is related to work distribution functions [66], which are the basic objects appearing in nonequilibrium fluctuation theorems [67] (such as the Jarzynski equality [68]).

The encoding of the lattice Schwinger model used in this work provides an effective theory that involves only matter fields after integrating out the gauge degrees of freedom (see section 2.1). However, it is nevertheless possible to theoretically and also experimentally access the dynamics of the gauge fields. Specifically, due to Gauss' law, the electric field operators ${\hat{L}}_{n}$ can be expressed in terms of the spin operators used in the encoding,

$$\begin{eqnarray}&&{\hat{L}}_{n}=\displaystyle \frac{1}{2}\displaystyle \sum _{l=1}^{n}[{\hat{\sigma }}_{l}^{z}+{(-1)}^{l}],\end{eqnarray} \tag{ 6 }$$

where we assumed a vanishing background field ${\epsilon }_{0}=0$. By measuring the local magnetizations ${\hat{\sigma }}_{l}^{z}$, one obtains full spatial and temporal access to the gauge degrees of freedom.

In figure 6 we show the dynamics of the local electric fields ${E}_{n}(t)=\langle {\hat{L}}_{n}(t)\rangle$ for our protocol, starting from the initial state $| \mathrm{vac}\rangle$ and assuming a vanishing background field, i.e. ${E}_{n}(t=0)=0$. During the course of the time evolution under the Hamiltonian ${\hat{H}}_{{\rm{S}}}$, the creation of particle–antiparticle pairs is accompanied by the buildup of local electric fields to satisfy Gauss' law. As explained in the previous section, the dynamics alternates between regimes of particle generation and recombination, which results in an oscillatory behaviour of both, the total particle number density $\nu (t)$ and the local electric fields E_n(t).

Zoom In Zoom Out Reset image size

The energy cost for the creation of a particle–antiparticle pairs is not only due to the respective rest masses but also due to the associated change in the electric-field contribution E_g to the total energy. The respective energy density ${{ \mathcal E }}_{g}(t)={N}^{-1}{E}_{g}(t)$ is given by

$$\begin{eqnarray*}&&{{ \mathcal E }}_{g}=\displaystyle \frac{{g}^{2}a}{2N}\displaystyle \sum _{n=1}^{N-1}\langle {\hat{L}}_{n}^{2}(t)\rangle .\end{eqnarray*}$$

Figure 7 shows the time evolution of ${{ \mathcal E }}_{g}(t)$ for the same nonequilibrium protocol considered in figure 6. For comparison, the energy density contribution associated with the rest masses of the fermions, ${{ \mathcal E }}_{m}(t)=(m/2N){\sum }_{n=1}^{N}{(-1)}^{l}\langle {\hat{\sigma }}_{n}^{z}(t)\rangle$ is also included. The plots show that particle–antiparticle creation is always accompanied by an increase in electric field energy. Since the total energy is conserved, this implies that during the pair creation process, the kinetic energy density is continuously converted into ${{ \mathcal E }}_{g}$ and ${{ \mathcal E }}_{m}$. This changes in the phases of recombination, where particle–antiparticle pairs annihilate each other and where the released electric field and rest mass energy is analogously converted into an enhanced kinetic energy for the remaining particles.

Zoom In Zoom Out Reset image size

The electric field energy ${E}_{g}(t)$ can also be determined from the experimental data taken in [1]. According to equation (6) and based on the measured spin correlations for the matter fields, we show in figure 8 its dynamics from the experimental data. The experimental methods and postselection procedure used are described in detail in [1]. The discrepancy with respect to the ideal time evolution stems from both, discretization errors and experimental imperfections, as shown in figure 2 in [1] (which is based on the same experimental data set as the results shown in figure 8). We remark that the electric fields energies on the individual links and any other correlation function that can be recast in terms of the electric field operators ${\hat{L}}_{n}$ are also experimentally accessible.

Zoom In Zoom Out Reset image size

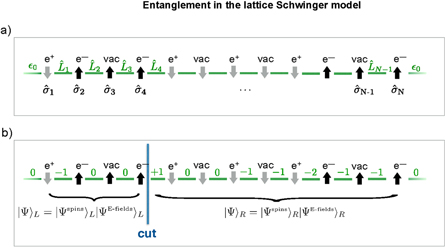
The entanglement entropy [69] is an important quantity for the theoretical characterization of quantum many-body dynamics. In the following, we study the real-time entanglement production during pair creation. We focus on the entanglement between two contiguous blocks in the spin system, which is equivalent to the entanglement between the respective blocks in the original fermionic description including the gauge degrees of freedom (see appendix for details). Indeed, when the system is encoded, the Hilbert space takes a factorized form (while in the initial formulation, it is not factorized due to the presence of Gauss's law); this form recovers the construction proposed in [41]. Therefore, it is possible to measure the entanglement in the original model directly in a pure spin system, which has the advantage that the partition into subsystems is always gauge invariant thereby avoiding known difficulties with tracing out parts of the system [41].

In the following, we consider the real-time dynamics of the half chain entanglement entropy,

$$\begin{eqnarray}&&S(t)=-{\mathrm{tr}}_{A}\{{\rho }_{A}(t)\mathrm{log}[{\rho }_{A}(t)]\}\end{eqnarray} \tag{ 7 }$$

with ${\rho }_{A}={\mathrm{tr}}_{B}\{\rho (t)\}$ denoting the reduced density matrix of the first $N/2$ lattice sites, obtained by tracing out the remaining system B. S(t) quantifies the entanglement between the left and the right half of the system, which is generated by the creation of particle–antiparticle pairs that are distributed across the two parts. As already shown in figure 4(c), the generation of entanglement decreases with increasing mass m, since particle creation becomes energetically costly for a large fermion mass. The dependence of the entanglement production in the electric field energy J is particularly interesting. The effective coupling between particles and antiparticles, mediated by the gauge bosons, increases with their relative spacing such that it becomes energetically unfavourable to separate particle–antiparticle pairs over large distances. This constrains the dynamics by reducing the number of particle–antiparticle pairs that can be shared between the left and the right half of the system. Accordingly, this leads to a reduction of entanglement for increasing J. In figure 9, we show the time evolution of the half chain entanglement entropy S(t) for two different electric coupling strengths $J/w=0$ and $J/w=0.2$ for varying system sizes. For the case of free particles, i.e., without coupling to the gauge fields (J = 0), the entanglement entropy exhibits a linear growth in time, characteristic for free fermionic theories. In the thermodynamic limit $N\to \infty$, the linear growth would continue for all times, but for finite system sizes $N\lt \infty$ it is cut off on a time scale ${wt}\propto N/2$. If $J\ne 0$, the entanglement growth follows initially approximately the free case up to a time scale ${t}_{J}={J}^{-1}$, beyond which the entanglement production is substantially slowed down. As the effective potential experienced by a particle–antiparticle pair increases linearly in the distance for nonzero J, the electric field suppresses the separation of spontaneously generated pairs over large distances. This, in consequence, reduces the amount of entanglement that can be produced. As these examples show, the quantum simulation of the Schwinger model allows for the observation of an intricate interplay between different parameter regimes, which can be studied in quantities not accessible to conventional experiments.

Zoom In Zoom Out Reset image size

In trapped-ion setups, spin degrees of freedom are obtained by restricting the dynamics to two (meta-) stable Zeeman levels of the internal electronic level structure of the ions [2, 3]. The use of focused laser beams acting on these levels allows one to realize single-qubit operations by inducing individually addressed AC-Stark shifts (${\hat{H}}_{\mathrm{AC}}^{n}\sim {\hat{\sigma }}_{n}^{z}$) and Rabi flops (${\hat{H}}_{\mathrm{RF}(\theta )}^{n}\sim \cos (\theta ){\hat{\sigma }}_{n}^{x}+\sin (\theta ){\hat{\sigma }}_{n}^{y}$). Spin–spin interactions are realized using a global laser field coupling the internal levels to external vibrational degrees of freedom. Here, we assume an implementation based on the so-called Mølmer–Sørensen interaction [4–7] that is mediated by the motional centre of mass mode [2] and provides an infinite range, all-to-all two-body coupling $\hat{{H}_{0}}={J}_{0}{\sum }_{n,l}{\hat{\sigma }}_{n}^{x}{\hat{\sigma }}_{l}^{x}$, as assumed in section 2.2. This effective description of the spin–spin interaction neglects the motional degrees of freedom of the chain of ions, which is valid if the spin-motion coupling after a gate operation is negligible and the duration of the interaction is much larger than the period of the harmonic motion of the ions in the trap. This condition is well fulfilled in the considered experimental setting [2, 3], as the period of the harmonic motion is typically less than $1\,\mu {\rm{s}}$ and the gate duration is longer than $50\,\mu {\rm{s}}$.

Our simulation protocol requires the decoupling of individual spins from the infinite-range coupling $\hat{{H}_{0}}={J}_{0}{\sum }_{n\gt l}{\hat{\sigma }}_{n}^{x}{\hat{\sigma }}_{l}^{x}$ (see figures 3(c), (d)), which can be achieved in different ways. For example, one may strongly detune individual ions from the laser fields that induce the Mølmer–Sørensen interaction by applying strong addressed AC Stark shifts [72, 73]. Alternatively, one can split the ion crystal into multiple chains during a single experiment, such that only the ions that take part in the long-range interaction form a connected crystal that interacts with the laser light. This flexible scheme requires the use of micrometer-scale ion traps which increases the experimental complexity considerably [74, 75]. An alternative that can be implemented in a macroscopic trap, and which has been employed in [1], consists in the transfer of the population of the idling ions to additional electronic substates that are off-resonant with respect to the laser light inducing the gate operations [3]. This decoupling (recoupling) procedure will be referred to as hiding (unhiding) below.

The digital quantum simulation scheme introduced in section 2.2, allows one to realize the time evolution under the Hamiltonian ${\hat{H}}_{{\rm{S}}}$ by means of a stroboscopic sequence, which consists of the cyclic application of Hamiltonians that can be experimentally realized ${\hat{H}}_{1},{\hat{H}}_{2},\,\ldots {\hat{H}}_{n}$ (see figure 3). The Trotter error, i.e. the difference between the desired time evolution ${U}_{{\rm{S}}}={{\rm{e}}}^{-{\rm{i}}{\hat{H}}_{{\rm{S}}}t}$ and the evolution realized by the stroboscopic sequence ${U}_{\mathrm{sim}}={({{\rm{e}}}^{-{\rm{i}}{\hat{H}}_{1}t/n}...{{\rm{e}}}^{-{\rm{i}}{\hat{H}}_{n}t/n})}^{n}$ is bounded by [28]

$$\begin{eqnarray*}&&{U}_{{\rm{S}}}-{U}_{\mathrm{sim}}=\displaystyle \frac{{t}^{2}}{2n}\displaystyle \sum _{i,j}[{\hat{H}}_{i},{\hat{H}}_{j}]+\epsilon ,\end{eqnarray*}$$

where represents higher-order terms¹¹ . Hence, these errors are controllable and the accuracy of the Trotter decomposition can, in principle, be increased to any desired precision by increasing the number of time steps n for a given total time t. However, the implementation of the proposed scheme in trapped ions poses limits on the minimum length of the step size that can be used. In the presence of decoherence, this leads to practical limitations on the accuracy with which the dynamics can be realized. More specifically, in order to suppress undesired spin-motion coupling terms during the applied Mølmer–Sørensen gates (see section 4.1), we require a minimal length ${\rm{\Delta }}{t}_{\min }$ of the basic time windows that are used, such that ${\omega }_{\mathrm{trap}}{\rm{\Delta }}{t}_{\min }\gg 1$. In the following, we consider typical experimental values, where ${\omega }_{\mathrm{trap}}$ takes values on the order of MHz [2, 3] and evaluate the Trotter error numerically for ${\rm{\Delta }}{t}_{I},{\rm{\Delta }}{t}_{{II}}\gg {\omega }_{\mathrm{trap}}^{-1}$ (compare figures 3(c), (d)). Local operations can be performed about an order of magnitude faster than entangling operations [3], and thus, one-qubit rotations are assumed to be instantaneous in our model. As figures 10 and 11 demonstrate, the Trotter error can be made sufficiently small to obtain a good resolution of the relevant features (see also experimental results in [1]). Thus, this error intrinsic to digital quantum simulation is well controlled and not a limiting factor.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

In this subsection, we discuss generic errors affecting the gate fidelity of the digital quantum simulation in trapped-ion systems. In the considered type of experiment [2, 3], the two main error sources impairing the required gate operations are (i) fluctuating coupling strengths of the Mølmer–Sørensen interaction and (ii) collective dephasing (see below). The first imperfection, fluctuations in the coupling strength $J=({J}_{0}+\delta J)$, is mainly due to intensity and beam pointing fluctuations of the laser beam, resulting in slightly modified interactions $\hat{{H}_{0}}=({J}_{0}+\delta J){\sum }_{n,l}{\hat{\sigma }}_{n}^{x}{\hat{\sigma }}_{l}^{x}$. The laser intensity fluctuations are slow on the time scale of a single simulation experiment, such that $\delta J$ can be considered to be constant within one experimental run. Consequently, the experiment effectively realizes an ensemble of coherent Hamiltonian evolutions with fluctuating interaction strength. The resulting expectation values are averages over trajectories corresponding to different values of $\delta J$.

The second major source of imperfections, dephasing between the two Zeeman levels that encode the spin states, is induced by fluctuating magnetic fields. Since the ions are typically only micrometers apart, all spins experience approximately the same field fluctuations, and the effect can be described in terms of Hamiltonian perturbations of the type ${\hat{H}}_{\mathrm{deph}}=\delta \omega {\sum }_{n}{\hat{\sigma }}_{n}^{z}$ with randomly varying coefficients $\delta \omega$. Again, on the time scale of a single experiment, $\delta \omega$ can be assumed to be time-independent such that we can take these experimental imperfections into account by averaging over an ensemble of trajectories for different values of $\delta \omega$. It is interesting to note that the considered ideal time evolutions (starting from the bare vacuum state shown in figure 4(a)) take place in the zero magnetization subspace, which forms a decoherence-free-subspace with respect to collective dephasing¹² .

We estimate the influence of these generic imperfections by performing a numerical simulation of the expected time evolution for the particle number density $\nu (t)$ and the rate function $\lambda (t)$. Throughout this article we use numerically exact simulations to study the dynamics in the Schwinger model. For this purpose we use exact diagonalization on the basis of a Lanczos algorithm with full reorthogonalization [76]. To include the effect of fluctuating coupling strengths and dephasing, we draw $\delta J$ and $\delta \omega$ randomly from uniform distributions. Figure 11 shows calculated data for a chain of ten ions with $J/w=m/w=1$. The solid line corresponds to the ideal case, while the circles represent the expected results taking the discussed experimental imperfections into account. Here, we considered fluctuations of the Mølmer–Sørensen coupling rate of 5% ($\delta J\in [-0.05,+0.05]{J}_{0}$) and a collective dephasing rate of $2.5 \%$ ($\delta \omega \in [-0.025,+0.025]{J}_{0}$). Assuming a Mølmer–Sørensen coupling rate of ${J}_{0}=4$ kHz, the circles correspond to Trotter steps where the elementary time window T (see figure 3) is 0.325 ms long. These fluctuations lead to a damping of the amplitude of the oscillations, though the frequency is retained. As these results show, the qualitative agreement including these errors remains satisfactory through realistic evolution times.

Additionally, if part of the qubit register is in the hiding states during a many-body interaction (see section 4.1), different phase shifts should be taken into account for ions that participate in the Mølmer–Sørensen interaction and for those that are transferred to hiding levels. Figure 11 contains a numerical simulation including this effect (crosses), where we consider the internal levels used in [1]. These results have been obtained by adding terms ${\hat{H}}_{\mathrm{deph}}=\delta \omega {\sum }_{n}{\hat{\sigma }}_{n}^{z}+\delta \omega ^{\prime} {\sum }_{l}{\hat{\sigma }}_{l}^{z}$ for each time window, where the first (second) sum includes ions that occupy regular (hiding) states. This leads only to minor corrections, as we show in figure 11. The error model above captures the dominating sources of imperfections in the considered setting. The effect of imperfect local operations on non-hidden qubits is negligible compared to the errors discussed above, since they can be performed with a much higher accuracy than multi-qubit entangling gate operations. In particular, if only a finite set of local operations is required, fidelities larger than ${F}_{\mathrm{local}}=0.99$ can be reached [3].

The use of hiding/unhiding techniques (see section 4.1) generates another source of imperfections in the simulated time evolution. If the applied hiding pulses fail to transfer a quantum state from the computational basis states to the corresponding hiding states¹³ $| \uparrow \rangle \to | {h}_{\uparrow }\rangle$, $| \downarrow \rangle \to | {h}_{\downarrow }\rangle$, or unhiding pulses fail to transfer the quantum states back, the many-body operation will not act on the ions as intended and thus induces many-body errors that are difficult to correct for. However, as we describe in the following, postselection techniques can be employed to detect and filter out this type of error without affecting the desired unitary evolution. Such a postselection scheme can for example be realized as follows. For each step in the protocol that involves a Mølmer–Sørensen gate acting on a subset of ions, suitable hiding operations are performed, followed by the action of the quantum gate, and the corresponding unhiding operations. Following these steps, a measurement of the population residing in the hiding levels is performed. If population is detected in the hiding levels, the experimental run is discarded. This way, only events that involve a failure of both the hiding and the unhiding pulse on a single ion (in a single hiding-unhiding step) remain undetected, which, however is strongly suppressed¹⁴ . Apart from a controllable residual error that can be suppressed to any desired accuracy, decoupling errors lead therefore only to a reduction of the rate at which simulation data can be acquired, but do not impair the desired unitary evolution.

In [1], an alternative postselection scheme has been applied to ensure that the final state fulfills Gauss' law. This involves measurements of the total magnetization $\hat{M}={\sum }_{n}{\hat{\sigma }}_{n}^{z}$ at the end of simulated time evolution. Due to charge conservation in the Schwinger model, $\hat{M}$ is a conserved quantity under the dynamics induced by ${\hat{H}}_{{\rm{S}}}$. The simulations performed in [1] have been carried out in the zero-charge subspace, starting from the initial state $| \uparrow \downarrow \uparrow \downarrow ...\rangle$. Using the employed decoupling and measurement techniques (see [1, 3]), single hiding/unhiding errors can lead to measurement results that correspond to a nonzero magnetization of the spin system. This subset of errors could therefore be detected and filtered out by postselection.

We remark that digital quantum simulation schemes allow one in principle to use quantum error correction schemes to ensure that the desired sequence of gates is carried out with high fidelity. The postselection techniques discussed here provide an alternative route that is easier to realize experimentally and allows one to filter out the dominant errors.