Abstract
Josephson circuits provide a realistic physical setup where the light–matter fine structure constant can become of order one, allowing to reach a regime dominated by non-perturbative effects beyond standard quantum optics. Simple processes, such as spontaneous emission, thus acquire a many-body character, that can be tackled using a new description of the time-dependent state vector in terms of quantum-superposed coherent states. We find that spontaneous atomic decay at ultrastrong coupling leads to the emission of spectrally broad Schrödinger cats rather than of monochromatic single photons. These cats states remain partially entangled with the emitter at intermediate stages of the dynamics, even after emission, due to a large separation in time scales between fast energy relaxation and exponentially slow decoherence. Once decoherence of the qubit is finally established, quantum information is completely transfered to the state of the emitted cat.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Introduction
Photons describe the granular structure of the electromagnetic field radiated by single coherent sources, such as atoms and quantum dots. These quanta of light constitute well-defined monochromatic excitations because the spontaneous emission rate Γ is much smaller than the transition frequency Δ of an emitter. More precisely, for atomic decay in three-dimensional space [1], the width of the transition lines,  , also defines a dimensionless coupling constant
, also defines a dimensionless coupling constant  involving two small factors: the ratio of the atomic dipole
involving two small factors: the ratio of the atomic dipole  to the photon wavelength λ, and the vacuum fine structure constant
to the photon wavelength λ, and the vacuum fine structure constant  . Typically
. Typically  , so that the light–matter coupling to a 3D continuum,
, so that the light–matter coupling to a 3D continuum,  , is vanishingly small.
, is vanishingly small.
With the advent of microwave quantum optics in superconducting one-dimensional waveguides [2–9], the coupling constant can reach the still small value  . Thus, a coupling of order one can only be attained by tweaking the fine structure constant itself. This requires the use of superconducting waveguides with high impedance, since
. Thus, a coupling of order one can only be attained by tweaking the fine structure constant itself. This requires the use of superconducting waveguides with high impedance, since  can be interpreted as the ratio of the vacuum impedance
can be interpreted as the ratio of the vacuum impedance  to the quantum of resistance
to the quantum of resistance  . Long chains of Josephson junctions [10–13] constitute low-loss metamaterials for the propagation of microwave photons with characteristic impedance Z up to the order of RK, allowing to obtain values of the coupling constant
. Long chains of Josephson junctions [10–13] constitute low-loss metamaterials for the propagation of microwave photons with characteristic impedance Z up to the order of RK, allowing to obtain values of the coupling constant  of order one. This physical regime reveals anomalous scattering properties of photons [14–18] impinging on a non-trivial dressed vacuum [19]. This Letter aims at answering a seemingly simple question: is the radiation from a single emitter still described by a discrete photon in the ultrastrong coupling regime?
of order one. This physical regime reveals anomalous scattering properties of photons [14–18] impinging on a non-trivial dressed vacuum [19]. This Letter aims at answering a seemingly simple question: is the radiation from a single emitter still described by a discrete photon in the ultrastrong coupling regime?
Clearly, the radiation released for  is strongly non-monochromatic, because ultrafast energy relaxation processes gives a large broadening of the atomic transition lines. In addition to modified spectral properties, drastic effects also occur in the quantum statistics of the radiation. Indeed, in contrast to spontaneous decay at weak coupling, where the photon state emerges as an n = 1 Fock excitation [1], the radiated field at ultrastrong coupling contains states with photon number larger than one. This surprising result can be understood as follows: photons with energy much smaller or much larger than the atomic transition frequency can be excited because one is not limited to resonant transitions in the non-perturbative regime of quantum electrodynamics (QED). But for low energy photons, the large available energy and the strong coupling constant make favorable the creation of multiple photon excitations. Infact, we find that the full quantum state of the electromagnetic field possesses a simple structure given by an optical Schrödinger cat, namely a superposition of strongly displaced coherent states. We stress that cat states obtained by spontaneous decay in a large impedance environment are very different from the cats obtained in cavities [20], for two reasons. First, as already mentioned above, the radiation is spectrally broad at ultrastrong coupling, and thus the resulting cat states are rather localized in the time domain rather than in frequency. Secondly, we find that these cat states display an intrinsic loss of coherence at longer times than the sudden time scale T1 associated to energy relaxation, but shorter than the long decoherence time T2 for complete memory loss of the initial atomic state. The separation of time scales
is strongly non-monochromatic, because ultrafast energy relaxation processes gives a large broadening of the atomic transition lines. In addition to modified spectral properties, drastic effects also occur in the quantum statistics of the radiation. Indeed, in contrast to spontaneous decay at weak coupling, where the photon state emerges as an n = 1 Fock excitation [1], the radiated field at ultrastrong coupling contains states with photon number larger than one. This surprising result can be understood as follows: photons with energy much smaller or much larger than the atomic transition frequency can be excited because one is not limited to resonant transitions in the non-perturbative regime of quantum electrodynamics (QED). But for low energy photons, the large available energy and the strong coupling constant make favorable the creation of multiple photon excitations. Infact, we find that the full quantum state of the electromagnetic field possesses a simple structure given by an optical Schrödinger cat, namely a superposition of strongly displaced coherent states. We stress that cat states obtained by spontaneous decay in a large impedance environment are very different from the cats obtained in cavities [20], for two reasons. First, as already mentioned above, the radiation is spectrally broad at ultrastrong coupling, and thus the resulting cat states are rather localized in the time domain rather than in frequency. Secondly, we find that these cat states display an intrinsic loss of coherence at longer times than the sudden time scale T1 associated to energy relaxation, but shorter than the long decoherence time T2 for complete memory loss of the initial atomic state. The separation of time scales  at ultrastrong coupling, see figure 1, illustrates again the stark difference with the weak-coupling regime of quantum optics, where
at ultrastrong coupling, see figure 1, illustrates again the stark difference with the weak-coupling regime of quantum optics, where  , and will be one of the main focus of the rest of the paper.
, and will be one of the main focus of the rest of the paper.
Figure 1. Left panel: decoherence process  with typical decay time T2, for increasing dimensionless coupling
with typical decay time T2, for increasing dimensionless coupling  (with coherent state number
(with coherent state number  , as required to reach convergence in the respective regimes). In all computations,
, as required to reach convergence in the respective regimes). In all computations,  and
and  . Right panel: energy relaxation process
. Right panel: energy relaxation process  with typical decay time T1, for the same parameters. For
with typical decay time T1, for the same parameters. For  , decoherence and relaxation times fulfill the usual relation
, decoherence and relaxation times fulfill the usual relation  , but for
, but for  the two time scales are widely different, with
the two time scales are widely different, with  , see text for a physical discussion of this effect.
, see text for a physical discussion of this effect.
Download figure:
Standard image High-resolution imageMethodology
Having presented the physics at play, we must emphasize that the computational aspects of QED at ultrastrong coupling are far from trivial, due to the breakdown of perturbation theory [19, 21, 22]. In contrast to cavity-QED at ultrastrong coupling [23–25], the Hilbert space is unmanageable for high impedance waveguides because: (i) a large number of electromagnetic modes are involved, up to  for long chains of Josephson junctions; (ii) the average total number of photons
for long chains of Josephson junctions; (ii) the average total number of photons  is larger than one. For the case
is larger than one. For the case  considered in the following, one obtains up to
considered in the following, one obtains up to  photons, so that the full quantum mechanical problem requires to tackle more than
photons, so that the full quantum mechanical problem requires to tackle more than  quantum states, well beyond the reach of brute force diagonalization. Based on the physical idea that coherent states are the most stable quantum states at ultrastrong coupling [26–28], we propose here a new methodology for harnessing cat states which relies on an efficient computational algorithm. This technique is not only conceptually simpler than state of the art methods [29–33], but also very powerful.
quantum states, well beyond the reach of brute force diagonalization. Based on the physical idea that coherent states are the most stable quantum states at ultrastrong coupling [26–28], we propose here a new methodology for harnessing cat states which relies on an efficient computational algorithm. This technique is not only conceptually simpler than state of the art methods [29–33], but also very powerful.
We will specify our study to the standard model of waveguide-QED, described by the Hamiltonian:
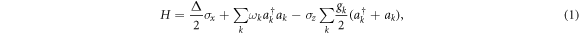
defining the light–matter coupling gk of a given mode with frequency  to the two-level atom, described by Pauli matrices
to the two-level atom, described by Pauli matrices  and transition frequency Δ. At variance with quantum optics conventions, we have intentionally written the atomic splitting as a
and transition frequency Δ. At variance with quantum optics conventions, we have intentionally written the atomic splitting as a  term, in order to emphasize the natural selection of coherent states caused by the
term, in order to emphasize the natural selection of coherent states caused by the  light–matter coupling. Hence, the bare atomic ground state is
light–matter coupling. Hence, the bare atomic ground state is ![$| g\rangle =[| \uparrow \rangle -| \downarrow \rangle ]/\sqrt{2}$](https://content.cld.iop.org/journals/1367-2630/19/2/023036/revision2/njpaa5deaieqn34.gif) in our notation. The dimensionless coupling strength α can be encapsulated from the spectral density
in our notation. The dimensionless coupling strength α can be encapsulated from the spectral density  , with
, with  the plasma frequency. We assume here a linear dispersion relation
the plasma frequency. We assume here a linear dispersion relation  , with unit speed of light in the medium, which is justified for atomic transitions well below
, with unit speed of light in the medium, which is justified for atomic transitions well below  . In addition, we do not consider here the important effect of coupling the high impedance finite-size Josephson waveguide to 50 Ω lines, which will restrict the spectrum to a set of discrete resonances (slightly broadened by the contacts). However, for a long-enough Josephson array, the limits in resolution will be well-below the characteristic scales of the system. Finally, we consider purely unitary dynamics, assuming that extrinsic losses, apart from the coupling to external contacts, are negligible.
. In addition, we do not consider here the important effect of coupling the high impedance finite-size Josephson waveguide to 50 Ω lines, which will restrict the spectrum to a set of discrete resonances (slightly broadened by the contacts). However, for a long-enough Josephson array, the limits in resolution will be well-below the characteristic scales of the system. Finally, we consider purely unitary dynamics, assuming that extrinsic losses, apart from the coupling to external contacts, are negligible.
As discussed above, the state vector is represented at all times by superposed coherent states [26–28]:
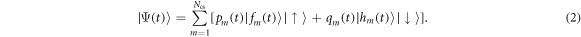
Here the set of amplitudes  are complex and time dependent, and a set of discrete multimode coherent states are introduced:
are complex and time dependent, and a set of discrete multimode coherent states are introduced: ![$| {f}_{m}(t)\rangle ={{\rm{e}}}^{{\sum }_{k=1}^{{N}_{\mathrm{modes}}}[{f}_{m}(k,t){a}_{k}^{\dagger }-{f}_{m}^{* }(k,t){a}_{k}]}| 0\rangle $](https://content.cld.iop.org/journals/1367-2630/19/2/023036/revision2/njpaa5deaieqn40.gif) . This decomposition allows in principle to target an arbitrary state of the full Hilbert space (with an exponential cost). One must note a strong difference here with the standard Glauber–Sudarshan decomposition, which relies on a continuous expansion of the state vector onto coherent states. Because of the large number of modes involved in waveguide QED at ultrastrong coupling, the continuous representation is not suitable for numerical purposes. Our discrete expansion (2) can however be understood as a discretized version of the continuous integral representation of an arbitrary wavefunction onto coherent states. Most importantly, we argue in this paper that physical states obtained from standard protocols (such as spontaneous emission) can be efficiently simulated with a discrete set of coherent states, showing only a polynomial cost in the number of modes Nmodes and coherent states Ncs. This computational gain was previously demonstrated for the full ground state of (1), and is here extended to the dynamics, allowing to simulate for the first time large systems, up to thousands of electromagnetic modes.
. This decomposition allows in principle to target an arbitrary state of the full Hilbert space (with an exponential cost). One must note a strong difference here with the standard Glauber–Sudarshan decomposition, which relies on a continuous expansion of the state vector onto coherent states. Because of the large number of modes involved in waveguide QED at ultrastrong coupling, the continuous representation is not suitable for numerical purposes. Our discrete expansion (2) can however be understood as a discretized version of the continuous integral representation of an arbitrary wavefunction onto coherent states. Most importantly, we argue in this paper that physical states obtained from standard protocols (such as spontaneous emission) can be efficiently simulated with a discrete set of coherent states, showing only a polynomial cost in the number of modes Nmodes and coherent states Ncs. This computational gain was previously demonstrated for the full ground state of (1), and is here extended to the dynamics, allowing to simulate for the first time large systems, up to thousands of electromagnetic modes.
Technically, the exact Schrödinger dynamics controlled by the Hamiltonian (1) can be obtained from the real Lagrangian density:
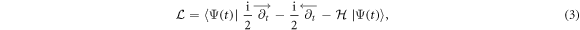
by applying the time-dependent variational principle [34],  , upon arbitrary variations of the state vector (2). This results in Euler–Lagrange equations
, upon arbitrary variations of the state vector (2). This results in Euler–Lagrange equations  for the set of variables
for the set of variables  , which can be solved by numerical integration [35–38] using a specially devised algorithm (see
, which can be solved by numerical integration [35–38] using a specially devised algorithm (see
We provide here clear proof of the good convergence of our algorithm. First, the left panel of figure 2 shows how the time-dependent error  vanishes with the number of coherent states, for the deep ultracoupling regime
vanishes with the number of coherent states, for the deep ultracoupling regime  . Here, the error is defined by the squared norm
. Here, the error is defined by the squared norm  of the auxiliary state
of the auxiliary state  , which is zero for the exact Schrödinger dynamics. Clearly the error is already small at all times for a single coherent state
, which is zero for the exact Schrödinger dynamics. Clearly the error is already small at all times for a single coherent state  , and goes quickly to zero with increasing number of terms in the decomposition equation (2). The precise scaling of the algorithm with Ncs is demonstrated in the right panel of figure 2. We find that the error (here computed at a finite and fixed time T = 80) decreases typically with an inverse square power
, and goes quickly to zero with increasing number of terms in the decomposition equation (2). The precise scaling of the algorithm with Ncs is demonstrated in the right panel of figure 2. We find that the error (here computed at a finite and fixed time T = 80) decreases typically with an inverse square power ![${[{N}_{\mathrm{cs}}]}^{-2}$](https://content.cld.iop.org/journals/1367-2630/19/2/023036/revision2/njpaa5deaieqn49.gif) , independently of the coupling strength α. This shows that our methodology is based on a physically well-motivated decomposition of the state vector, and is not tied to a particular regime of the spin-boson model. The coherent state expansion of the time-dependent state vector (2) thus provides numerically accurate results in all regimes of coupling for a small computational effort.
, independently of the coupling strength α. This shows that our methodology is based on a physically well-motivated decomposition of the state vector, and is not tied to a particular regime of the spin-boson model. The coherent state expansion of the time-dependent state vector (2) thus provides numerically accurate results in all regimes of coupling for a small computational effort.
Figure 2. Left panel: error  as a function of time with respect to the exact Schrödinger dynamics for the challenging case
as a function of time with respect to the exact Schrödinger dynamics for the challenging case  (here the atomic splitting is
(here the atomic splitting is  ), which drops rapidly to zero with increasing Ncs. Right panel: error
), which drops rapidly to zero with increasing Ncs. Right panel: error  at a fixed time T = 80, as a function of coherent state numbers for
at a fixed time T = 80, as a function of coherent state numbers for  ,
,  (intermediate ultracoupling regime) and
(intermediate ultracoupling regime) and  (deep ultrastrong coupling regime), showing a scaling
(deep ultrastrong coupling regime), showing a scaling ![${[{N}_{\mathrm{cs}}]}^{-2}$](https://content.cld.iop.org/journals/1367-2630/19/2/023036/revision2/njpaa5deaieqn57.gif) .
.
Download figure:
Standard image High-resolution imageDecoherence versus relaxation times
We consider first the important issue of the time scales governing the physics in the ultrastrong coupling regime. For this purpose, we prepare the initial state as ![$| {\rm{\Psi }}(t=0)\rangle =| 0\rangle \otimes | \uparrow \rangle =| 0\rangle \otimes [| g\rangle +| e\rangle ]/\sqrt{2}$](https://content.cld.iop.org/journals/1367-2630/19/2/023036/revision2/njpaa5deaieqn58.gif) in a superposition of the two bare atomic levels, and with the environment in its vacuum. Since the two-level splitting is described by a
in a superposition of the two bare atomic levels, and with the environment in its vacuum. Since the two-level splitting is described by a  coupling in equation (1), one expects precession and decay to zero of the transverse spin component
coupling in equation (1), one expects precession and decay to zero of the transverse spin component  on a time scale T2, and relaxation of the longitudinal term
on a time scale T2, and relaxation of the longitudinal term  towards its finite equilibrium value on a time scale T1. This standard behavior is well obeyed in the weak-coupling regime
towards its finite equilibrium value on a time scale T1. This standard behavior is well obeyed in the weak-coupling regime  , with
, with  , as seen from the dot-dashed green curve in the first two panels of figure 1. For the intermediate value
, as seen from the dot-dashed green curve in the first two panels of figure 1. For the intermediate value  (full blue curve), precession of
(full blue curve), precession of  is nearly overdamped, as is well established [21].
is nearly overdamped, as is well established [21].
Remarkably, the ultrastrong coupling regime  (dashed red curve) shows a striking decoupling between the decoherence time T2 and the energy relaxation time T1, with
(dashed red curve) shows a striking decoupling between the decoherence time T2 and the energy relaxation time T1, with  . The underlying physics can be anticipated: energy relaxation, related to emission of radiation, occurs on the short time scale T1, because the excited atomic level is strongly damped at large α. This is clearly seen from the rapid saturation of
. The underlying physics can be anticipated: energy relaxation, related to emission of radiation, occurs on the short time scale T1, because the excited atomic level is strongly damped at large α. This is clearly seen from the rapid saturation of  in the middle panel of figure 1 at
in the middle panel of figure 1 at  . However, rapid decoherence is prohibited because the atom is dressed by its electromagnetic environment [19] on a large spatial scale
. However, rapid decoherence is prohibited because the atom is dressed by its electromagnetic environment [19] on a large spatial scale  (here
(here  , corresponding to the threshold of full localization). Decoherence thus takes a considerable time
, corresponding to the threshold of full localization). Decoherence thus takes a considerable time  for the complete relaxation of all quantum correlations between the dressed atom and the is larger than one,radiated field. This effect is seen by the very slow decay of
for the complete relaxation of all quantum correlations between the dressed atom and the is larger than one,radiated field. This effect is seen by the very slow decay of  (dashed red curve in the left panel of figure 1). Indeed, for
(dashed red curve in the left panel of figure 1). Indeed, for  and
and  ,
,  , which was not reached at the final time of our simulations. As we will see in the following, this separation of time scales is key to understanding the physics at play, due to its strong impact on the structure of the emitted light.
, which was not reached at the final time of our simulations. As we will see in the following, this separation of time scales is key to understanding the physics at play, due to its strong impact on the structure of the emitted light.
Quantum states of spontaneous emission
We turn to the emission protocol, taking now the bare excited level of the atom ![$| {\rm{\Psi }}(t=0)\rangle =| 0\rangle \otimes [| \uparrow \rangle +| \downarrow \rangle ]/\sqrt{2}=| 0\rangle \otimes | e\rangle $](https://content.cld.iop.org/journals/1367-2630/19/2/023036/revision2/njpaa5deaieqn77.gif) as the initial state. According to Wigner–Weisskopf theory [1] valid at weak coupling
as the initial state. According to Wigner–Weisskopf theory [1] valid at weak coupling  , one expects spontaneous emission of a single photon and decay of the atom towards its bare ground state. Although our theory (2) is based on coherent states and not Fock excitations, we can show that it does recover the standard quantum optics results at
, one expects spontaneous emission of a single photon and decay of the atom towards its bare ground state. Although our theory (2) is based on coherent states and not Fock excitations, we can show that it does recover the standard quantum optics results at  , while providing a simple physical picture in the ultrastrong coupling regime. For this purpose, we plot in figure 3 the real part of the coherent state amplitudes
, while providing a simple physical picture in the ultrastrong coupling regime. For this purpose, we plot in figure 3 the real part of the coherent state amplitudes  and
and  (for m = 1, 2) for
(for m = 1, 2) for  , as a function of the spatial separation x along the waveguide (the atom is located at x = 0). Here we choose a time
, as a function of the spatial separation x along the waveguide (the atom is located at x = 0). Here we choose a time  long enough that the system has fully relaxed to its dressed ground state. The emitted wavepacket is clearly seen at a distance
long enough that the system has fully relaxed to its dressed ground state. The emitted wavepacket is clearly seen at a distance  , due to ballistic propagation of the wavefront, and the displacements satisfy the following relations:
, due to ballistic propagation of the wavefront, and the displacements satisfy the following relations:  (in addition,
(in addition,  (not shown)). Within the spatial region
(not shown)). Within the spatial region  where the atom is dressed by its static surrounding cloud, a different set of relations is observed:
where the atom is dressed by its static surrounding cloud, a different set of relations is observed:  . Factoring each coherent state in real space
. Factoring each coherent state in real space  simplifies the wavefunction (2):
simplifies the wavefunction (2):
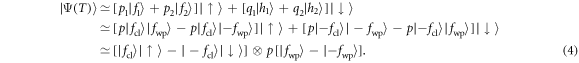
The last line in (4) is straightforwardly interpreted as the absence of correlations between the dressed qubit ![$| {{\rm{\Psi }}}_{\mathrm{cl}}\rangle \equiv [| {f}_{\mathrm{cl}}\rangle | \uparrow \rangle -| -{f}_{\mathrm{cl}}\rangle | \downarrow \rangle ]/\sqrt{2}$](https://content.cld.iop.org/journals/1367-2630/19/2/023036/revision2/njpaa5deaieqn90.gif) (which comprises both the atom and its entangled neighboring cloud in the waveguide) and the emitted wavepacket
(which comprises both the atom and its entangled neighboring cloud in the waveguide) and the emitted wavepacket ![$| {{\rm{\Psi }}}_{\mathrm{wp}}\rangle \equiv \sqrt{2}p[| {f}_{\mathrm{wp}}\rangle -| -{f}_{\mathrm{wp}}\rangle ]$](https://content.cld.iop.org/journals/1367-2630/19/2/023036/revision2/njpaa5deaieqn91.gif) . This is physically expected as the system relaxes at long times to a unique dressed ground state, while emitting a stream of electromagnetic radiation carrying the excess energy but no quantum correlations with the atom. We stress that the above expressions for
. This is physically expected as the system relaxes at long times to a unique dressed ground state, while emitting a stream of electromagnetic radiation carrying the excess energy but no quantum correlations with the atom. We stress that the above expressions for  and
and  are only approximate, as small quantum corrections arise at increasing α [26, 27], which are accounted for by the terms
are only approximate, as small quantum corrections arise at increasing α [26, 27], which are accounted for by the terms  in the expansion (2).
in the expansion (2).
Figure 3. Real part of the coherent state amplitudes in real space  and
and  (for m = 1, 2) at a time T = 200 long enough that the emitted wavepacket is uncorrelated from the entanglement cloud associated to the dressed atomic ground state (denoted as a shaded area). Here
(for m = 1, 2) at a time T = 200 long enough that the emitted wavepacket is uncorrelated from the entanglement cloud associated to the dressed atomic ground state (denoted as a shaded area). Here  , and
, and  , with
, with  (top panel),
(top panel),  (middle panel), and
(middle panel), and  (bottom panel).
(bottom panel).
Download figure:
Standard image High-resolution imageThe approximate wavefunction (4) nicely recovers the result of Wigner–Weisskopf theory in the quantum optics regime  . Indeed, in this case the displacements in the dressing cloud are vanishingly small,
. Indeed, in this case the displacements in the dressing cloud are vanishingly small,  , and thus
, and thus ![$| {{\rm{\Psi }}}_{\mathrm{cl}}\rangle =| 0\rangle [| \uparrow \rangle -| \downarrow \rangle ]/\sqrt{2}\equiv | 0\rangle | g\rangle $](https://content.cld.iop.org/journals/1367-2630/19/2/023036/revision2/njpaa5deaieqn104.gif) , so that the atom has correctly relaxed to its bare ground state. The quantum state describing the emitted light also simplifies, since the displacements in the wavepacket are small,
, so that the atom has correctly relaxed to its bare ground state. The quantum state describing the emitted light also simplifies, since the displacements in the wavepacket are small,  . A first-order Taylor expansion of the coherent state gives
. A first-order Taylor expansion of the coherent state gives  , which is the expected one-photon Fock state. The monochromatic nature of the emitted light can be seen from the spatiotemporal oscillations of the fields in the upper panel of figure 3, with an envelope controlled by the underdamped dynamics of the qubit (first panel of figure 1 for
, which is the expected one-photon Fock state. The monochromatic nature of the emitted light can be seen from the spatiotemporal oscillations of the fields in the upper panel of figure 3, with an envelope controlled by the underdamped dynamics of the qubit (first panel of figure 1 for  ). Moving towards the ultrastrong coupling regime for increasing α values (middle and lower panel in figure 3), two major changes occur. First, the displacements in the entanglement cloud
). Moving towards the ultrastrong coupling regime for increasing α values (middle and lower panel in figure 3), two major changes occur. First, the displacements in the entanglement cloud  penetrate deeper and deeper within the waveguide, due to the increase of the screening length LK with α, as shown by the shaded area in figure 3. Second, the emitted wavepacket becomes very localized temporally, with associated displacements that clearly grow in magnitude. This indicates that the radiation is spectrally broad, and that the number of emitted photons grows with increasing α, as was anticipated.
penetrate deeper and deeper within the waveguide, due to the increase of the screening length LK with α, as shown by the shaded area in figure 3. Second, the emitted wavepacket becomes very localized temporally, with associated displacements that clearly grow in magnitude. This indicates that the radiation is spectrally broad, and that the number of emitted photons grows with increasing α, as was anticipated.
Nature of spontaneously emitted cats
Let us finally analyze in more detail the quantum properties of the emitted radiation, starting with the approximate expression ![$| {{\rm{\Psi }}}_{{\rm{wp}}}\rangle =\sqrt{2}p[| {f}_{{\rm{wp}}}\rangle -| -{f}_{{\rm{wp}}}\rangle ]$](https://content.cld.iop.org/journals/1367-2630/19/2/023036/revision2/njpaa5deaieqn109.gif) for the emitted wavepacket. Although this state is a Fock state when the average number of emitted photons is close to one, as shown above, it clearly turns into an odd parity Schrödinger cat when the displacements grow large, as seen for
for the emitted wavepacket. Although this state is a Fock state when the average number of emitted photons is close to one, as shown above, it clearly turns into an odd parity Schrödinger cat when the displacements grow large, as seen for  in the lower panel in figure 3. In order to check this idea more precisely, we compute the Wigner distribution of the emitted wavepacket. In contrast to photons released into a cavity [20, 39], we stress again that the radiation is not purely monochromatic, due to the significant damping effect on the atom caused by the strong coupling to the waveguide. Accordingly, following standard practice [40], one uses an optimized temporal filter w(t) of the output signal. The filter function w(t) is defined as to match precisely the shape of any of the wavefronts in figure 3 (which show the same amplitude), in the spatial domain where the emitted signal is decoupled from the short distance cloud (here in the approximate range
in the lower panel in figure 3. In order to check this idea more precisely, we compute the Wigner distribution of the emitted wavepacket. In contrast to photons released into a cavity [20, 39], we stress again that the radiation is not purely monochromatic, due to the significant damping effect on the atom caused by the strong coupling to the waveguide. Accordingly, following standard practice [40], one uses an optimized temporal filter w(t) of the output signal. The filter function w(t) is defined as to match precisely the shape of any of the wavefronts in figure 3 (which show the same amplitude), in the spatial domain where the emitted signal is decoupled from the short distance cloud (here in the approximate range  ). For the values of
). For the values of  in figure 3, a measurement time T = 200 is sufficient to ensure this decoupling, but for the computation of figure 4 with
in figure 3, a measurement time T = 200 is sufficient to ensure this decoupling, but for the computation of figure 4 with  , a longer time T = 900 was required, due to the increase in T2.
, a longer time T = 900 was required, due to the increase in T2.
Figure 4. Wigner distribution  at time T = 900 identifying a one-photon state at
at time T = 900 identifying a one-photon state at  (left panel) and a partially coherent cat state at
(left panel) and a partially coherent cat state at  (right panel) with two positive classical lobes and a negative region with reduced amplitude compared to
(right panel) with two positive classical lobes and a negative region with reduced amplitude compared to  for a fully coherent cat. The function was computed with
for a fully coherent cat. The function was computed with  and
and  .
.
Download figure:
Standard image High-resolution imageOwing to the linear dispersion in the waveguide, the averaging can be performed spatially by defining an effective creation operator  , in which a Θ-function is used to take out the static bound component of the screening cloud. The global scale of the filter function w(t) is set by imposing standard commutation relation for the effective mode, namely
, in which a Θ-function is used to take out the static bound component of the screening cloud. The global scale of the filter function w(t) is set by imposing standard commutation relation for the effective mode, namely ![$[b,{b}^{\dagger }]=1$](https://content.cld.iop.org/journals/1367-2630/19/2/023036/revision2/njpaa5deaieqn121.gif) . The Wigner distribution [20] is then computed using the standard expression
. The Wigner distribution [20] is then computed using the standard expression  , with the symmetrized correlation function
, with the symmetrized correlation function  . For
. For  , the phase space distribution in the left panel of figure 4 shows the characteristic circular form of the n = 1 Fock state with negative quasi-probability
, the phase space distribution in the left panel of figure 4 shows the characteristic circular form of the n = 1 Fock state with negative quasi-probability  at the origin.
at the origin.
At ultrastrong coupling for  , the emitted radiation undergoes radical changes, as shown in the right panel of figure 4. The Wigner distribution now presents two positive lobes (signature of the two classical configurations of the cat), but also a negative region near the origin, fingerprint of the characteristic quantum interference, or 'whiskers', of a Schrödinger cat. Surprisingly, the maximum negative amplitude does not reach the expected value
, the emitted radiation undergoes radical changes, as shown in the right panel of figure 4. The Wigner distribution now presents two positive lobes (signature of the two classical configurations of the cat), but also a negative region near the origin, fingerprint of the characteristic quantum interference, or 'whiskers', of a Schrödinger cat. Surprisingly, the maximum negative amplitude does not reach the expected value  of a perfectly coherent cat, although our system does not present any extrinsic source of decoherence for the optical modes (such as leaks into a 3D continuum). We argue that the physical source of decoherence is the dressed qubit itself, a very unusual feature. This phenomenon can be understood from the qubit dynamics shown in figure 1, in relation to the separation of time scales
of a perfectly coherent cat, although our system does not present any extrinsic source of decoherence for the optical modes (such as leaks into a 3D continuum). We argue that the physical source of decoherence is the dressed qubit itself, a very unusual feature. This phenomenon can be understood from the qubit dynamics shown in figure 1, in relation to the separation of time scales  . Indeed, the cat state is emitted on a short scale
. Indeed, the cat state is emitted on a short scale  in the ultrastrong coupling regime, due to the sudden release of energy. But the atom maintains its coherence on a longer time scale
in the ultrastrong coupling regime, due to the sudden release of energy. But the atom maintains its coherence on a longer time scale  due to its long-range spatial entanglement with the waveguide, since
due to its long-range spatial entanglement with the waveguide, since  does not decay. From the no-cloning theorem [1], the quantum information stored in the dressed atom state cannot be transfered to the wavepacket for times t ≪ T2, and thus the coherence of the emitted cat state is only partial at intermediate timescales. This explains why the negative lobe of the cat state in the right panel of figure 4 does not quite reach the maximal value
does not decay. From the no-cloning theorem [1], the quantum information stored in the dressed atom state cannot be transfered to the wavepacket for times t ≪ T2, and thus the coherence of the emitted cat state is only partial at intermediate timescales. This explains why the negative lobe of the cat state in the right panel of figure 4 does not quite reach the maximal value  .
.
We have to point out that a definite phase is seen in the cat state of figure 4, which evolves as the state propagates between the emitter and the measurement setup. Its absolute value is tied to the original form of the Hamiltonian (1), where the qubit is seen to couple to the first quadrature of the field. Moreover, it must be stressed that a true measurement setup will take place outside the waveguide, which must be adapted to a low impedance environment. It may be that phase information is ultimely lost in the final output field, as pointed out previously in the context of anisotropic dielectrics [41], hence perhaps modifying the cat structure. Interestingly, this problem bears some similarity to transport in interacting quantum wires (Luttinger liquids [42]), which can be described by squeezed plasmonic modes. The interaction fingerprints visible in the conductance of an infinite wire are indeed suppressed once the wire is smoothly connected to non-interacting leads [43, 44]. The question of impedance matching in ultra-strongly coupled waveguides has not been addressed to our knowledge in the recent circuit-QED literature [14–18].
We conclude our analysis of the emitted cat by displaying its actual photon content. In the left panel of figure 5, we show the spectrally resolved photon number density, which is obtained as previously by cutting out the static part of the field tied to the atom. In the quantum optics regime  , the lineshape is a narrow Lorentzian centered at the bare transition frequency Δ. For increasing α, the peak is shifted to lower frequencies due to the dressing of the atom by the bosonic bath, but more remarkably, its lineshape becomes spectrally very broad. This illustrates again the fact that the cat state generated by spontaneous emission has a rather localized character in the time domain. We stress that the number of emitted photons has to vanish for zero frequency modes, because the coupling constant gk vanishes at
, the lineshape is a narrow Lorentzian centered at the bare transition frequency Δ. For increasing α, the peak is shifted to lower frequencies due to the dressing of the atom by the bosonic bath, but more remarkably, its lineshape becomes spectrally very broad. This illustrates again the fact that the cat state generated by spontaneous emission has a rather localized character in the time domain. We stress that the number of emitted photons has to vanish for zero frequency modes, because the coupling constant gk vanishes at  . This is also true for the curve
. This is also true for the curve  , although the downturn of the curve can barely be seen on the graph, due to the strong renormalization of the emission frequency to tiny frequencies. The size of the cat can be measured by integrating the photon density curves, giving the photon numbers shown in the right panel of figure 5, both for the wavepacket (solid line) and the total wavefunction (dashed line) comprising wavepacket and entanglement cloud. At ultrastrong coupling for
, although the downturn of the curve can barely be seen on the graph, due to the strong renormalization of the emission frequency to tiny frequencies. The size of the cat can be measured by integrating the photon density curves, giving the photon numbers shown in the right panel of figure 5, both for the wavepacket (solid line) and the total wavefunction (dashed line) comprising wavepacket and entanglement cloud. At ultrastrong coupling for  , the wavepacket contains
, the wavepacket contains  photons, in agreement with the cat size in figure 4, with an average total photon number of
photons, in agreement with the cat size in figure 4, with an average total photon number of  , which highlights the complexity of the quantum problem at play, involving more than
, which highlights the complexity of the quantum problem at play, involving more than  quantum states.
quantum states.
Figure 5. Left: emission spectrum showing photon number density  in the wavepacket as a function of mode number k, for
in the wavepacket as a function of mode number k, for  , with
, with  . Right: integrated photon number in the wavepacket (solid line) and in the total wavefunction (dashed line).
. Right: integrated photon number in the wavepacket (solid line) and in the total wavefunction (dashed line).
Download figure:
Standard image High-resolution imageTo summarize, we have found that Schrödinger cat states are spontaneously radiated by a single emitter in an infinite high impedance medium at ultrastrong coupling. These cats show unusual properties in comparison to standard quantum optics protocols [20, 45]: they are spectrally very broad and partially quantum coherent at intermediate stages of the dynamics, due to a strong separation in time scales between the slow decoherence and the fast energy relaxation of the emitter. After complete information loss of an arbitrary initial state of the qubit ![$[u| g\rangle +v| e\rangle ]\otimes | 0\rangle $](https://content.cld.iop.org/journals/1367-2630/19/2/023036/revision2/njpaa5deaieqn143.gif) , the qubit relaxes to a unique many-body ground state
, the qubit relaxes to a unique many-body ground state  , associated to the polarization in the waveguide. Quantum information is then preserved in a generic cat state
, associated to the polarization in the waveguide. Quantum information is then preserved in a generic cat state ![$| \mathrm{GS}\rangle \otimes [(u+v)| +f\rangle +(u-v)| -f\rangle ]$](https://content.cld.iop.org/journals/1367-2630/19/2/023036/revision2/njpaa5deaieqn145.gif) of the radiated field at long times. However, impedance matching of the waveguide to a low-impedance external measurement apparatus may drastically affect the quantum correlations of spontaneous emission (as well as the structure of inelastically scattered light [15, 17]), a generic problem that will be addressed in a future study.
of the radiated field at long times. However, impedance matching of the waveguide to a low-impedance external measurement apparatus may drastically affect the quantum correlations of spontaneous emission (as well as the structure of inelastically scattered light [15, 17]), a generic problem that will be addressed in a future study.
Acknowledgments
We thank H Baranger, A Chin, T Grall, T Meunier, A Nazir, J Puertas-Martinez, M Schiró and I Snyman for useful discussions, and especially N Roch for stimulating several aspects of this work. Financial support from the Nanoscience Foundation is also recognized.
Appendix. Derivation of the dynamical equations
The starting point of the method is to represent the state vector at an arbitrary time by an expansion onto coherent states:
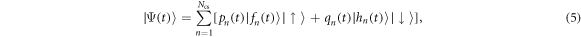
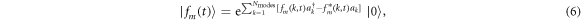
where the set of variables  are complex and time dependent, with
are complex and time dependent, with  . Following the time-dependent variational principle [34], we define the real Lagrangian density
. Following the time-dependent variational principle [34], we define the real Lagrangian density  , from which arbitrary variations of the state vector give the simple Euler–Lagrange equations
, from which arbitrary variations of the state vector give the simple Euler–Lagrange equations  for our set of variables. For the spin-boson model [21], the equations explicitly read:
for our set of variables. For the spin-boson model [21], the equations explicitly read:
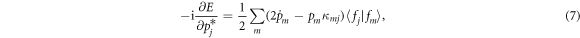
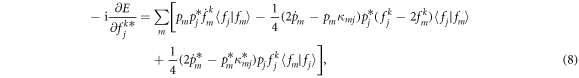
Identical equations (up to a minus sign) are obtained for the variables qn and hkn. We have denoted here  the average energy, whose explicit expression is:
the average energy, whose explicit expression is:

where we have defined  ,
,  ,
,  ,
,  .
.
In contrast to the dynamics with a single coherent state [36, 38], one encounters here a computational difficulty [35], because time-derivatives  of all possible coherent state amplitudes enter the dynamical equation ruling a given field fjk in equation (8) through the parameter
of all possible coherent state amplitudes enter the dynamical equation ruling a given field fjk in equation (8) through the parameter  in equation (9). Indeed, for stability reasons it is crucial to formulate the dynamical equations in an explicit form
in equation (9). Indeed, for stability reasons it is crucial to formulate the dynamical equations in an explicit form ![${\dot{f}}_{j}^{k}=F[v]$](https://content.cld.iop.org/journals/1367-2630/19/2/023036/revision2/njpaa5deaieqn157.gif) , where F is only a functional of the variables
, where F is only a functional of the variables  without reference to their time derivatives. Numerical inversion in order to bring the system into explicit form is however prohibitive (unless the number of modes is small, for instance in the case of the Wilson discretization [37], which is not adapted to study the bath dynamics), as it would cost
without reference to their time derivatives. Numerical inversion in order to bring the system into explicit form is however prohibitive (unless the number of modes is small, for instance in the case of the Wilson discretization [37], which is not adapted to study the bath dynamics), as it would cost  operations. It turns out that a very convenient trick allows to make the inversion in
operations. It turns out that a very convenient trick allows to make the inversion in  operations, which is favorable provided
operations, which is favorable provided  , as is the case for very long Josephson arrays or broadband environments. First, we invert equations (7) and (8) by expliciting the
, as is the case for very long Josephson arrays or broadband environments. First, we invert equations (7) and (8) by expliciting the  dependence:
dependence:
defining the compact notation  ,
,  ,
,  , and
, and  , with
, with  ,
, ![${F}_{j}^{k}=-{\rm{i}}\partial E/\partial {f}_{k}^{j* }\,+\,(1/2)[{P}_{j}{p}_{j}^{* }\,+\,{P}_{j}^{* }{p}_{j}]{f}_{k}^{j}$](https://content.cld.iop.org/journals/1367-2630/19/2/023036/revision2/njpaa5deaieqn168.gif) , and the overlap matrices
, and the overlap matrices  and
and  . The evolution equation (11) is still not in explicit form, because the parameters
. The evolution equation (11) is still not in explicit form, because the parameters  explicitly depend on time derivatives in equation (9). However, we can now use equation (11) to replace all the
explicitly depend on time derivatives in equation (9). However, we can now use equation (11) to replace all the  terms in equation (9), which gives a closed equation for the κ matrix:
terms in equation (9), which gives a closed equation for the κ matrix:
Inverting this linear systems with  parameters provides the final
parameters provides the final  scaling of our algorithm. Of course the gain is important only provided that Ncs stays small during the unitary time evolution. We show now that the dynamics indeed converges rapidly for a surprisingly small number of coherent states, demonstrating that the decomposition (5) is physically well motivated.
scaling of our algorithm. Of course the gain is important only provided that Ncs stays small during the unitary time evolution. We show now that the dynamics indeed converges rapidly for a surprisingly small number of coherent states, demonstrating that the decomposition (5) is physically well motivated.








