Abstract
Both quantum mechanics and general relativity are based on principles that defy our daily intuitions, such as time dilation, quantum interference and entanglement. Because the regimes where the two theories are typically tested are widely separated, their foundational principles are rarely jointly studied. Recent works have found that novel phenomena appear for quantum particles with an internal structure in the presence of time dilation, which can take place at low energies and in weak gravitational fields. Here we briefly review the effects of time dilation on quantum interference and generalize the results to a variety of systems. In addition, we provide an extended study of the basic principles of quantum theory and relativity that are of relevance for the effects and also address several questions that have been raised, such as the description in different reference frames, the role of the equivalence principle and the effective irreversibility of the decoherence. The manuscript clarifies some of the counterintuitive aspects arising when quantum phenomena and general relativistic effects are jointly considered.
Export citation and abstract BibTeX RIS
1. Introduction
The interplay between quantum theory and general relativity offers many exciting and novel phenomena. The typical frameworks in which such an interplay is studied are quantum field theory in curved background or quantum gravity theories. Such frameworks are suited to describe high-energy phenomena, most of which lie far beyond near-future technological possibilities.
A series of recent works [1–3] has shown that, even at low energies and in the absence of quantum field effects, new phenomena can arise from the combination of quantum mechanical and relativistic effects. It was shown that time dilation causes entanglement between the center of mass of a quantum particle and its internal degrees of freedom. This effect takes place due to relativistic corrections to the dynamics of quantum systems, and has consequences for quantum interference of composite systems. The time dilation produced by Earth's gravity is sufficient to have a measurable influence on quantum interference in near-future experiments.
Here we give an overview of the findings, derive the effect for various systems and scenarios, and discuss the relevant physical concepts. While the phenomena can be described in a quantum field theory setting (see, e.g., appendix of [3]), a convenient theoretical framework for these phenomena is the quantum dynamics in first quantization with relativistic corrections. It highlights the relevant interplay between quantum mechanical and relativistic principles, which is not as apparent in the context of the more commonly studied relativistic quantum field theory. For this reason, several questions have been put forward regarding the predicted effects in our works [4–6], and the context in which these effects can appear. In addition, in contrast to our works, the low-energy limit of the interplay between quantum theory and gravity is often studied in the context of modified quantum theories, which include a collapse of the wave function [7, 8] or nonlinear quantum dynamics [9], and which are motivated by a fundamental transition to classicality. While we showed that time dilation can cause decoherence [3], our works do not fall into this class of models. In this manuscript we also provide an extended study of the relevant physical concepts that are pertinent to the results, and address the various questions. In the following, we give an overview of the issues addressed and the novel aspects that are discussed in this manuscript.
1.1. Overview of this manuscript
Time dilation in quantum interferometry has been the subject of a series of recent studies [1–3]. Related works and follow-up studies are summarized in section 1.2. In section 2 we review the basic principles and results of [1–3]: the basis of probing time dilation with classical and localized systems is reviewed in section 2.1, a summary of the Hamiltonian description of time dilation to lowest non-vanishing order is given in section 2.2, and a derivation of the general effect of time dilation on quantum interference is given in section 2.3. We discuss a variety of specific systems in section 3, generalizing the results from [1] to two-level systems in arbitrary initial states in section 3.1 and generalizing the results from [3] to arbitrary mixed states in section 3.2. A number of conceptual issues are studied in the following sections, which also address raised questions [4–6] (specific replies can be found in the arxiv version of this paper [arXiv:1508.03296] and in [10]). The description of the results in different reference frames is studied in section 4, the compatibility of the framework and results with basic principles of relativity, quantum theory and gravity is addressed in section 5, and the behavior of time dilation decoherence is discussed in section 6.
In particular, we clarify the reference frame independence in section 4, where we show that physically observable effects, such as fringes in an interference experiment, do not depend on the reference frame used to describe them. In section 4.1 we consider the example of a free-falling particle that is described by a free-falling and an accelerated observer. We further show how observers in relative motion use different descriptions for the same physical situation: in section 4.2 we study the coordinate dependence of the Hamiltonian and in section 4.3 we discuss how different observers can assign different amounts of entanglement to the same system. The equivalence principle, one of the main cornerstones of general relativity, is discussed in the context of the results in section 5.1, showing that it is always satisfied in the studied framework. The role of gravity is discussed in section 5.2. We elucidate in section 5.3 to what extent a first-quantized formalism is suitable to describe relativistic phenomena that do not involve quantum-field effects. We clarify in subsection 5.4 that there is no mass superselection rule for the physical regime under consideration, which is relativistic and thus not invariant under Galilean transformations. The behavior and nature of decoherence due to time dilation is discussed in section 6: the transition from reversible to practically irreversible loss of coherence is discussed in section 6.1 and in section 6.2 we discuss how the effective Gaussian decay arises. In the following sections, we briefly discuss in what sense the effect is universal (6.3), the relation between decoherence and classicality (6.4) and the difference to gravitational collapse models (6.5).
1.2. Summary of related studies
In recent years, a number of manuscripts have explored various aspects of time dilation in quantum interferometry. Starting in 2011, the effect of time dilation on matter-wave interferometry with internal clocks was first considered in [1], which generalized the classical 'twin paradox' to a quantum setting that involves superpositions. A similar scenario was also studied in [11]. Both works also addressed the discussion about the interpretation of an experiment with atomic fountains [12], namely whether the Compton frequency can be associated with a physical clock in quantum interferometry [13–17], and showed that this cannot be the case as it would lead to an additional observable effect on the interferometric visibility. While the time dilation analysis used for massive particles does not directly apply to the propagation of light, the generalization of [1] to optical interferometry was studied in [2, 18], where the Shapiro delay of a single photon can lead to a phase shift or loss of visibility in a quantum optical interferometer. This effect is considered for potential exploration in future space missions [19, 20], as well as in fiber optics based interferometry [21]. Focusing on the evolution of the internal degrees of freedom, the fundamental limits on the stability of clocks due to the time dilation induced entanglement between internal and external degrees of freedom were discussed in [22]. All these effects on quantum systems stem from the relativistic coupling between internal and external degrees of freedom due to time dilation, which was further studied in [23–25].
The effect described in [1] for a two-level system was recently experimentally simulated with a BEC [26]. In this experiment, a Stern–Gerlach type matter-wave interferometer on an atom chip was utilized, and an external inhomogeneous magnetic field was applied to simulate the effect of time dilation on the spin precession of the system. The results confirmed the predictions in [1] and opened a way to study self-interfering clocks in the laboratory. A new pathway for experiments to probe the time dilation induced effect was studied in [27], which proposed to use a single electron in a Penning trap that is in superposition of different radial states. The time dilation in this case is special relativistic, due to the non-inertial motion of the electron. A similar scenario including a rotating platform was described in [28].
In our recent work, we have studied how time dilation can lead to decoherence of composite quantum systems [3]. Some concepts related to the effect were discussed in [4–6, 10, 29], and some questions therein are addressed in this manuscript. The decoherence effect was further analyzed in [30], where it was compared to collisional decoherence and it was shown that revivals occur, albeit at very long time scales. The comparison to other decoherence sources was also studied in [31], showing that they mask time dilation induced decoherence in interference of hot systems with present day experimental capabilities. The time scale associated with the decoherence was also considered in [32], where the authors also explicitly show that the effect does not directly depend on external potentials. While our work focused on a fixed background space–time from Earth's gravitational field, [33] generalized the decoherence effect to space–times created by the system itself and a scenario that involves only gravitational interactions. In [34, 35] it was shown that clocks entangle with each other due to the backaction of their internal energies onto the space–time, which leads to a fundamental limit of their ability to measure time. A decoherence mechanism similar to decoherence due to time dilation was considered in [36], which studied loss of interference in a free-falling scenario due to different arrival times of amplitudes with different mass. Like time dilation induced decoherence, this effect can take place due to the mass-energy equivalence, but these two decoherence mechanisms are not the same. The time dilation induced entanglement and decoherence in a free-falling scenario was studied in [24], where also the difference to Newtonian effects was highlighted.
Related to the study of time dilation in quantum interferometry, recent works considered the equivalence principle in the context of the mass-energy equivalence that includes quantum superpositions of internal energies. This has led to the characterization of genuinely quantum mechanical violations of the equivalence principle [37], and studies of how the new violation parameters can be tested in dedicated experiments [38].
2. Review of the effect of time dilation on quantum systems
2.1. Time dilation in classical and quantum systems
In relativity theory, the physical time measured by clocks is the proper time τ. In contrast to Newtonian mechanics, the proper time depends on the velocity of the clock, as well as the background space–time along the world line γ of the clock:
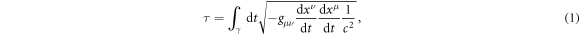
where  is some arbitrary coordinate time that parameterizes the clock's world line and
is some arbitrary coordinate time that parameterizes the clock's world line and  is the metric tensor expressed in the chosen system of coordinates
is the metric tensor expressed in the chosen system of coordinates  . A classic direct test of this prediction was performed by Hafele and Keating [39], using initially synchronized clocks that were sent on different world lines
. A classic direct test of this prediction was performed by Hafele and Keating [39], using initially synchronized clocks that were sent on different world lines  (on an airplane) and
(on an airplane) and  (on the ground), causing the clocks to record different proper times
(on the ground), causing the clocks to record different proper times  and
and  . The results confirmed the relativistic predictions for the velocity-dependent and gravitational contributions to the elapsed time as recorded by the different sets of clocks [40].
. The results confirmed the relativistic predictions for the velocity-dependent and gravitational contributions to the elapsed time as recorded by the different sets of clocks [40].
According to relativity, all clocks record the proper time and thus time dilation is universal in that it affects any clock in the same way, regardless of its internal composition or internal mechanisms. The experiment by Hafele and Keating used atomic clocks that are described by quantum mechanics. Atomic clocks operate by preparing a superposition of internal states, such as a superposition of the ground and a single excited state:  . This state will evolve in time, as it is not an eigenstate of the internal Hamiltonian, which we denote by H0. In the co-moving frame of such a clock that follows a fixed world line, the internal atomic state
. This state will evolve in time, as it is not an eigenstate of the internal Hamiltonian, which we denote by H0. In the co-moving frame of such a clock that follows a fixed world line, the internal atomic state  thus evolves according to
thus evolves according to

where τ is the proper time along the world line γ of this clock. Experiments such as the one by Hafele and Keating, or the more recent one by Chou et al [41], confirm that the internal evolution of atoms is governed by proper time as in equation (2), and as predicted by relativity. But while quantum physics is necessary to describe the atomic clocks, the external path that governs τ is classically well defined in all such experiments.
However, the possibility to prepare quantum states of external degrees of freedom opens the route for novel phenomena, as shown in a series of recent works [1–3]. When the clock can follow different world lines in superposition, time dilation causes entanglement between the center of mass of a quantum particle and its internal degrees of freedom. Conceptually, this follows directly from the above considerations: the internal dynamics makes the internal state evolve to  , where τ is the proper time along the path of the particle. If the particle follows two different world lines
, where τ is the proper time along the path of the particle. If the particle follows two different world lines  and
and  in superposition, as for example in a quantum interferometric experiment, the final state that describes both the internal and external degrees of freedom is
in superposition, as for example in a quantum interferometric experiment, the final state that describes both the internal and external degrees of freedom is
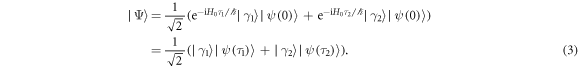
The resulting state is thus an entangled state between the internal degrees of freedom and the state of the center of mass. Such a state is conceptually different than what has been probed so far in the context of time dilation, captured by equation (2). Here, two independent amplitudes of one and the same system are superposed that evolve according to different proper times. The linearity of quantum mechanics together with time dilation, assuming that both are valid in this regime, give rise to an entangled state. This entanglement and its measurable consequences have been discussed in the context of matter-waves [1, 11], photons [2, 18] and purely gravitational interactions [31]. An important consequence is that this effect leads to decoherence of the particle's motional degrees of freedom, if the internal degrees of freedom constitute a sufficiently large 'bath' [3].
2.2. Hamiltonian describing time dilation
A system acting as an 'ideal clock' is a point-like system with some internal dynamics that measures the passage of time. Let  be the Lagrangian describing the internal dynamics in the comoving frame. The action of the ideal clock is then given by
be the Lagrangian describing the internal dynamics in the comoving frame. The action of the ideal clock is then given by
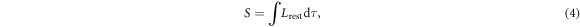
where  is the proper time element and the integral is taken over the world line of the particle. In classical physics this is a single world line, while in quantum physics the clock can follow several world lines in superposition. The expression for proper time for a post-Newtonian metric to lowest order in
is the proper time element and the integral is taken over the world line of the particle. In classical physics this is a single world line, while in quantum physics the clock can follow several world lines in superposition. The expression for proper time for a post-Newtonian metric to lowest order in  is given by
is given by
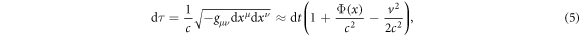
where t, x and v = dx/dt are, respectively, the coordinate time, position and velocity of the system and  is the gravitational potential. For time dilation it is sufficient to consider the external dynamics as fixed and that the world lines are pre-assigned: the internal dynamics evolves according to the world line's proper time according to equation (2). In a general scenario, the evolution of the external degrees of freedom (i.e. the position of the particle) is not pre-assigned and has to be treated dynamically. A useful approach is to derive the classical Hamiltonian corresponding to (4) by a Legendre transformation. The Hamiltonian represents only the generator of time translation for a specific coordinate time, thus general covariance is less transparent in the Hamiltonian formulation. However, covariance is guaranteed in the observed effects, as the final results will always depend on a combination of coordinates that just represent proper time, as can be verified by computing specific scenarios in different coordinates (see below). Using the metric (5), the Hamiltonian corresponding to (4) is
is the gravitational potential. For time dilation it is sufficient to consider the external dynamics as fixed and that the world lines are pre-assigned: the internal dynamics evolves according to the world line's proper time according to equation (2). In a general scenario, the evolution of the external degrees of freedom (i.e. the position of the particle) is not pre-assigned and has to be treated dynamically. A useful approach is to derive the classical Hamiltonian corresponding to (4) by a Legendre transformation. The Hamiltonian represents only the generator of time translation for a specific coordinate time, thus general covariance is less transparent in the Hamiltonian formulation. However, covariance is guaranteed in the observed effects, as the final results will always depend on a combination of coordinates that just represent proper time, as can be verified by computing specific scenarios in different coordinates (see below). Using the metric (5), the Hamiltonian corresponding to (4) is
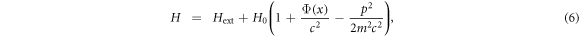
where H0 and  are the internal and external Hamiltonians, respectively, and we have separated the constant mass contribution mc2 from H0 (see also [3], methods). For a free particle,
are the internal and external Hamiltonians, respectively, and we have separated the constant mass contribution mc2 from H0 (see also [3], methods). For a free particle,  plus relativistic corrections. Any additional external forces and potentials V(x) acting on the system, such as those required to keep it at some height on Earth or to perform an interferometric experiment, will contribute to
plus relativistic corrections. Any additional external forces and potentials V(x) acting on the system, such as those required to keep it at some height on Earth or to perform an interferometric experiment, will contribute to  in (6). The additional terms that couple H0 to x and p are responsible for time dilation and are just a reformulation of equation (5). The Hamiltonian (6) simply reproduces the effect of time dilation and captures its parametrization in given coordinates, in particular, its dependence on the position and velocity. Thus, for classical particles, Hamiltonian (6) captures some of the best-tested effects in modern physics. The coupling with momentum,
in (6). The additional terms that couple H0 to x and p are responsible for time dilation and are just a reformulation of equation (5). The Hamiltonian (6) simply reproduces the effect of time dilation and captures its parametrization in given coordinates, in particular, its dependence on the position and velocity. Thus, for classical particles, Hamiltonian (6) captures some of the best-tested effects in modern physics. The coupling with momentum,  , is simply the velocity-dependent special relativistic time dilation, while the coupling with position,
, is simply the velocity-dependent special relativistic time dilation, while the coupling with position,  , is the gravitational redshift. Describing the dynamics on a fixed background space–time in terms of a Hamiltonian is standard procedure and higher order relativistic corrections can also be obtained within a consistent framework [42].
, is the gravitational redshift. Describing the dynamics on a fixed background space–time in terms of a Hamiltonian is standard procedure and higher order relativistic corrections can also be obtained within a consistent framework [42].
The Hamiltonian treatment allows one to directly study how quantum systems behave in the presence of time dilation, by considering the canonically quantized dynamics. Note that both, time dilation and the superposition principle are implicitly built into the formalism and they have been extensively studied independently: in all classical tests of time dilation, the external degrees of freedom x and p that appear in (6) were classical, even though the internal degrees of freedom governed by H0 were quantized. In quantum interferometry, the quantum nature of the external degrees of freedom x and p is probed, but time dilation is not considered and the observed gravitational effects could be explained by Newtonian gravity. The combination of these two has not been tested yet, and provides a scenario where the quantum dynamics in the presence of post-Newtonian effects can be probed. In particular, time dilation acting on the clocks can result in the entanglement with the clocks' motional degrees of freedom, a purely quantum mechanical effect. Using standard techniques to integrate out the internal degrees of freedom, one obtains the equation of motion for the particle's center of mass, described by a master equation, equation (22) below (derived in [3]). In general, this equation predicts the loss of coherence of particles in superposition along different world lines.
2.3. Quantum interference in the presence of time dilation
A clock will be affected by time dilation as described by equation (6). The quantum effect is the entanglement between the internal states of the clock and the external degrees of freedom. This in turn affects the coherence of the quantum superposition of the external degrees of freedom. The simplest example is a two-way interferometer, where the system is split into superposition of two world lines, and the interference of the particle is measured after recombining the two paths, as schematically depicted in the space-time diagram in figure 1. The interferometric visibility is a physical measure of the coherence of the system, given by the off-diagonal elements of the state of interest. This can be computed directly from equation (3), taking the trace over the internal degrees of freedom (denoted by the subscript 0): ![$V=2| \langle {\gamma }_{1}\,| {\mathrm{Tr}}_{0}[\rho ]| \,{\gamma }_{2}\rangle | $](https://content.cld.iop.org/journals/1367-2630/19/2/025011/revision2/njpaa5d92ieqn21.gif) , where
, where  and
and  are the two pre-assigned world lines that the system follows in superposition. With
are the two pre-assigned world lines that the system follows in superposition. With  being the total proper time difference between the two world lines and
being the total proper time difference between the two world lines and  the initial state of the internal degrees of freedom, the visibility is
the initial state of the internal degrees of freedom, the visibility is
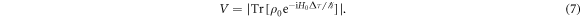
The above expression has a few noteworthy features. It is coordinate invariant, since proper time and the internal Hamiltonian H0 (defined as the Hamiltonian in the rest frame of the system) are invariant. The internal Hamiltonian can be arbitrary, which reflects the universality of time dilation. The internal state  is arbitrary, which means that the visibility is affected by internal pure states, as discussed in [1], as well as internal mixed states, as in [3]. The visibility is unaffected if either
is arbitrary, which means that the visibility is affected by internal pure states, as discussed in [1], as well as internal mixed states, as in [3]. The visibility is unaffected if either  , such that the two world lines have the same proper time, or if
, such that the two world lines have the same proper time, or if  , i.e. the system is in an eigenstate of the internal Hamiltonian H0, such that there is no clock. We will discuss these features in more detail below and in a few concrete examples.
, i.e. the system is in an eigenstate of the internal Hamiltonian H0, such that there is no clock. We will discuss these features in more detail below and in a few concrete examples.
Figure 1. World lines of a two-way interferometer. The particle is split at laboratory time t = 0 to follow two paths in superposition, which are recombined again at  to observe interference. If the two paths have different proper times τ, and if the particle has internal degrees of freedom that are not in their energy eigenstate, its quantum interference is modulated by the envelope given in equation (7).
to observe interference. If the two paths have different proper times τ, and if the particle has internal degrees of freedom that are not in their energy eigenstate, its quantum interference is modulated by the envelope given in equation (7).
Download figure:
Standard image High-resolution image3. Time dilation in quantum interferometry for specific systems
We will now consider a few concrete examples to highlight how the interference visibility of various systems is affected in the presence of time dilation.
3.1. Internal two-level system
The simplest system affected by time dilation is a two-level system prepared in a coherent superposition of its internal states, as discussed in [1]. The internal state is thus  , as above, and the Hamiltonian is
, as above, and the Hamiltonian is  , with
, with  . Note that expression (7) can be rewritten as
. Note that expression (7) can be rewritten as
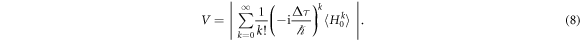
For the pure initial superposition with equal amplitudes, we have

which gives
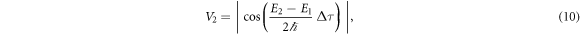
where the subscript 2 stands for the two-level system. For the simple example of the system's center of mass being stationary but in a superposition of two different heights x1 and x2, we have  to lowest order in
to lowest order in  , where t is the laboratory time and
, where t is the laboratory time and  is the gravitational potential at height x. As the proper time difference depends only on the difference in gravitational potential, it persists even in the limit of a homogeneous gravitational field, a well-known result for the gravitational redshift. Thus to lowest order, the visibility is simply
is the gravitational potential at height x. As the proper time difference depends only on the difference in gravitational potential, it persists even in the limit of a homogeneous gravitational field, a well-known result for the gravitational redshift. Thus to lowest order, the visibility is simply  , as in [1]. In a recent experiment, the above predictions have been simulated in a BEC interference setup in the presence of inhomogeneous magnetic fields [26].
, as in [1]. In a recent experiment, the above predictions have been simulated in a BEC interference setup in the presence of inhomogeneous magnetic fields [26].
For a mixed internal state, the visibility is affected by time dilation as well. A generic state of a 2-level system is  , with
, with  . In this case, we have
. In this case, we have
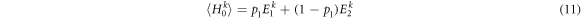
and the interferometric visibility becomes
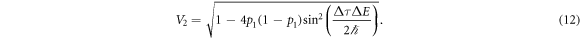
For a mixed state with  , equation (12) reduces exactly to equation (10), which was obtained for an internal coherent superposition. Thus internal coherence is not required for the modulation of the visibility. However, if the state is in a pure energy eigenstate (
, equation (12) reduces exactly to equation (10), which was obtained for an internal coherent superposition. Thus internal coherence is not required for the modulation of the visibility. However, if the state is in a pure energy eigenstate ( or
or  ), the visibility remains always V = 1 and the interference is not affected by time dilation. In the intermediate case, the visibility will periodically drop to
), the visibility remains always V = 1 and the interference is not affected by time dilation. In the intermediate case, the visibility will periodically drop to  at
at  for
for  , and revive to
, and revive to  at
at  . The behavior of the visibility for a single two-level internal degree of freedom is illustrated in figure 2(a).
. The behavior of the visibility for a single two-level internal degree of freedom is illustrated in figure 2(a).
Figure 2. The interferometeric visibility in the presence of time dilation for a variety of systems. (a) A single 2-level system for various occupation numbers, as given by equation (10). (b) A single n-level system with equidistant and equally populated levels for various n. (c) A single 10-level system with a random distribution of levels. (d) 5 internal degrees of freedom, with an equal but random distribution of ten internal levels. For sufficiently many internal systems, no revival occurs for all practical purposes and the loss of coherence is governed by equation (18).
Download figure:
Standard image High-resolution image3.2. N internal degrees of freedom with arbitrary levels
The results above can be readily generalized to arbitrary many internal degrees of freedom each having arbitrary internal levels. For the systems of interest, all N internal degrees of freedom follow the same world-lines, namely the one of the center of mass, and their spatial extension is much smaller than the size over which the metric field considerably changes (such that it still acts as an ideal probe). If these N internal systems are initially uncorrelated, we have  . Each internal system can be in a general mixed state
. Each internal system can be in a general mixed state
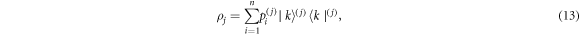
where the superscript j denotes the Hilbert space of the jth internal state,  is the energy eigenbasis with eigenvalues
is the energy eigenbasis with eigenvalues  and where
and where  are the populations for the respective energy levels. Note that we neglect internal coherence, as this is not relevant for the effect as illustrated above. Also, for simplicity we assumed all N internal degrees of freedom to have the same number of levels n, which in general does not need to be the case. Using these initial states to compute
are the populations for the respective energy levels. Note that we neglect internal coherence, as this is not relevant for the effect as illustrated above. Also, for simplicity we assumed all N internal degrees of freedom to have the same number of levels n, which in general does not need to be the case. Using these initial states to compute  in equation (8) yields
in equation (8) yields
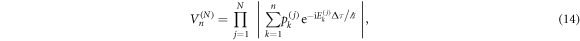
where V has now the subscript n that stands for the number of internal levels and the superscript N that stands for the number of internal degrees of freedom. While V2 for the 2-level system showed a simple periodic reduction and revival of interference, the case considered here gives rise to more complicated behavior that depends on the level structure of the various internal components. For sufficiently many internal states, the visibility will initially drop and effectively diminish without revival at reasonable times (see also discussion in section 6.1). The visibility for various systems as described by equation (14) is shown in figure 2.
For many internal levels we can approximate them to be continuously distributed. If all N states have the same spectrum and are in a thermal state, the initial state is
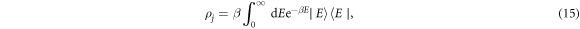
where  with the Boltzmann constant kB and temperature T. In this case, the visibility (7) becomes
with the Boltzmann constant kB and temperature T. In this case, the visibility (7) becomes
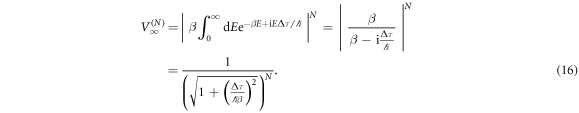
In the limit  , which is satisfied for the small proper time differences on Earth even for macroscopic systems, the above expression is approximately
, which is satisfied for the small proper time differences on Earth even for macroscopic systems, the above expression is approximately  . The same result for the visibility was also derived in [3, 28] for the case of N internal harmonic oscillators. More generally, in the limit of small proper time differences, we can directly Taylor expand equation (7) which yields
. The same result for the visibility was also derived in [3, 28] for the case of N internal harmonic oscillators. More generally, in the limit of small proper time differences, we can directly Taylor expand equation (7) which yields

where  is the variance in internal energy. This expression is valid for
is the variance in internal energy. This expression is valid for  , but holds for arbitrary internal states. This was one of the examples discussed in [3]. For the simple example of a particle (with many internal degrees of freedom) being stationary but in a superposition of two different heights x1 and x2, the loss of visibility is governed by a Gaussian decay with a characteristic decoherence time
, but holds for arbitrary internal states. This was one of the examples discussed in [3]. For the simple example of a particle (with many internal degrees of freedom) being stationary but in a superposition of two different heights x1 and x2, the loss of visibility is governed by a Gaussian decay with a characteristic decoherence time
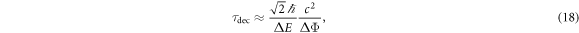
where  is the difference in gravitational potentials between the two heights, which in the homogeneous limit becomes
is the difference in gravitational potentials between the two heights, which in the homogeneous limit becomes  , with g the gravitational acceleration on Earth. Note that the internal energy variance
, with g the gravitational acceleration on Earth. Note that the internal energy variance  is for thermal states directly proportional to the heat capacity as
is for thermal states directly proportional to the heat capacity as  . Using the three-dimensional Einstein model to get a simple dependence on the amount of internal degrees of freedom N gives
. Using the three-dimensional Einstein model to get a simple dependence on the amount of internal degrees of freedom N gives  . Other models for the internal energy were discussed in [31].
. Other models for the internal energy were discussed in [31].
In this manuscript, we do not discuss the experimental feasibility of probing the effect for any of the systems considered above. Experimental verification of the above predictions, as well as experimental exploration of this novel regime of quantum theory and relativity are highly desirable. We note that probing the decoherence for a large thermal system remains very challenging [31], while the effect for smaller systems with controlled internal degrees of freedom seems feasible in near-future experiments [1, 27, 28, 43]. Studies of well-suited systems and specifically designed experimental efforts will help towards experimental realization.
4. Reference frame independence
While entanglement between quantum degrees of freedom is most conveniently studied in a Hilbert space formulation of quantum mechanics, such a formulation is not manifestly covariant. The relativistic invariance of the predicted results may thus not be immediately transparent, which has motivated some concerns [4, 6]. Here we clarify that the coherence of a system is an observable quantity with a physical meaning within an experimental setup (for example, by measuring the visibility in a Mach–Zehnder interferometer). For any specified experiment, the observed coherence will not depend on the reference frame, as guaranteed by the coordinate invariance of action (4) from which the effect is derived. For the case of two superposed world lines, decoherence only depends on the proper time difference between them, equation (7), which is independent of the reference frame used to estimate it. The initial and final points of each world line have to be specified to make any meaningful statement about the total proper time. Decoherence does not depend on the reference frame but on the proper time difference between the amplitudes. Estimating the decoherence for various physical scenarios thus reduces to an exercise in classical relativity, computing the proper times along each interferometric path.
4.1. Example of a particle in free fall
Typically, coherence is measured in interferometric experiments, in which the wave packets have to be overlapped on, say, a beam-splitter. This case is the one considered in [1–3], where the superposed paths have common initial and final points (which may correspond to the first and second beam-splitter, or the source and detection points on a screen in a double-slit experiment). The outcomes do not depend on the choice of reference frame to describe the experiments, as is apparent from equation (7) (see also [24]). One may however also consider superimposed world-lines that do not meet on a final beam splitter. The coherence in such a scenario is not directly measurable as interference of the wave packets but it can be given a physical meaning in principle, for example by letting the beams interact with ancillary systems in the chosen space–time points and later performing appropriate measurements on the ancillae. Although less relevant for potential experiments, it can be instructive to study how such scenarios are described in different reference frames.
Decoherence depends only on the overall time dilation between the superposed amplitudes. One can consider an experiment performed in a uniformly accelerated laboratory, but with the particle in free fall in superposition of different amplitudes (as in [4]). For simplicity, we consider here a laboratory accelerating in flat space–time, instead of one fixed above Earth (the results coincide to leading order, in accordance with the equivalence principle). A particle is prepared at time t = 0 in superposition of two different heights, x1 and x2. We assume that the spread of each wavepacket around each point is negligible and that no additional force is acting on the particle, so each wavepacket will follow a classical free-falling trajectory, see figure 3(a). In order to estimate the coherence after some time tf, we can rely on equation (7) and have to calculate the proper time along the two world lines. Notice that this is an exercise in classical relativity for which quantum mechanics plays no particular role: we can as well consider the proper time of two classical clocks following the two said world lines. It is convenient to introduce inertial coordinates:

where X, T are Minkowski coordinates and x, t Rindler coordinates [44]. The two free-falling world lines are parameterized by Minkowski time T and have constant Minkowski positions X1, X2, respectively (note that x = X for  , so Xj = xj, j = 1, 2), with proper time equal to Minkowski coordinate time. Importantly, since we are seeking the proper time difference for equal final Rindler time, the two world lines have different final Minkowski times (see figure 3(b)), yielding the proper time difference
, so Xj = xj, j = 1, 2), with proper time equal to Minkowski coordinate time. Importantly, since we are seeking the proper time difference for equal final Rindler time, the two world lines have different final Minkowski times (see figure 3(b)), yielding the proper time difference

with  . Thus, for an accelerating observer the free-falling superposition appears to decohere. When looking at the same experiment from the point of view of a freely falling observer, the same proper time difference and thus the same loss of coherence is attributed. However, in the free-falling reference frame the experiment considered does not test coherence at a given time, rather the two amplitudes appear to be measured at different times.
. Thus, for an accelerating observer the free-falling superposition appears to decohere. When looking at the same experiment from the point of view of a freely falling observer, the same proper time difference and thus the same loss of coherence is attributed. However, in the free-falling reference frame the experiment considered does not test coherence at a given time, rather the two amplitudes appear to be measured at different times.
Figure 3. Two free-falling world lines as seen from an accelerated laboratory frame (a) and from a free-falling frame (b). The two world lines end on an equal-time plane in the laboratory frame (dashed lines), which appear as different times in the free-falling plane. The proper time difference between the world lines does not depend on the reference frame.
Download figure:
Standard image High-resolution imageOne can also ask whether decoherence is observed for measurements that are synchronous in the free-falling frame. This is a different experiment and there is no reason to expect the same result as before. Clearly, for particles at rest in flat space–time and measured at equal times in Minkowski coordinates, no proper time difference and thus no decoherence is observed. However, one should not be led to conclude that no decoherence (or, equivalently, no time dilation) can be ever observed for systems in free fall (as should also be clear from the exercise above). In a recent work [33], Gooding and Unruh have shown that the effect discussed here can provide decoherence in systems that are only subject to gravity (and thus are, by definition, in free fall).
Note that the above example of a free-falling particle is not the example considered in our works [1–3], in which it is assumed that the particle is held in superposition at fixed heights6
. For a particle in superposition at fixed heights in Rindler coordinates, and measured at equal Rindler times, one finds the proper time difference  confirming that decoherence will occur in this scenario. One can again ask whether decoherence is observed when the same accelerating particle is measured at equal times in a free-falling frame, which is straight-forward to confirm.
confirming that decoherence will occur in this scenario. One can again ask whether decoherence is observed when the same accelerating particle is measured at equal times in a free-falling frame, which is straight-forward to confirm.
In the examples above the two world lines do not meet, as opposed to the situation depicted in figure 1. For the latter, no arbitrariness in the choice of measurement space-like planes arises, which is thus of main physical relevance. We also stress that it is assumed in [1–3] and in the situation described by figure 1 that the interferometric paths perfectly overlap on the final beam splitter, as opposed to the scenario considered in [36]. The latter work describes a related effect, where loss of interference in a free-falling scenario takes place due to different arrival times of amplitudes with different mass. While this effect can occur due to the mass-energy equivalence, which is also responsible for the time dilation induced decoherence, these two decoherence effects are not the same and occur in different physical scenarios. Time dilation induced decoherence takes place even when the interfering paths perfectly overlap, as in figure 1, and depends only on the time dilation between the paths, not on the arrival times of the beams.
4.2. Coordinate dependence of the Hamiltonian
A Hamiltonian is defined with respect to a given slicing of space–time in equal-time surfaces and so it is a coordinate-dependent object. However, the covariance of the overall effect is guaranteed by the fact that the Hamiltonian is obtained via Legendre transform from the action (4), which is manifestly coordinate independent7 . For any given experiment, different observers will predict the same results, although they will in general use different Hamiltonians.
It can be useful to see explicitly how the interaction terms change when changing reference frame. A simple way to do this is to recall that the Hamiltonian is the 0th component of the 4-momentum. The relation between 4-momentum and rest energy is, in arbitrary coordinates
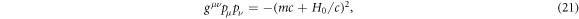
with the signature (− + + +) for the metric and where  is the inverse of the metric tensor (see [3]). The Hamiltonian in the given reference frame is then obtained by solving for p0, which provides
is the inverse of the metric tensor (see [3]). The Hamiltonian in the given reference frame is then obtained by solving for p0, which provides  as a function of H0, pj and
as a function of H0, pj and  (through the position-dependent metric
(through the position-dependent metric  ). The effective coupling between H0 and pj and
). The effective coupling between H0 and pj and  are then obtained by perturbative expansion8
. Thus, the metric is all that is needed to know the form of the interaction
are then obtained by perturbative expansion8
. Thus, the metric is all that is needed to know the form of the interaction  in the given coordinates.
in the given coordinates.
The coupling between position and internal energy in equation (6) arises from the expansion of  , where Φ is Earth's gravitational potential. In a free-falling frame, this coupling disappears, leaving only the coupling with momentum. As a result, internal and external degrees of freedom will develop a different amount of entanglement in different reference frames, which is discussed in the next section.
, where Φ is Earth's gravitational potential. In a free-falling frame, this coupling disappears, leaving only the coupling with momentum. As a result, internal and external degrees of freedom will develop a different amount of entanglement in different reference frames, which is discussed in the next section.
4.3. Reference frame dependence of the entanglement between internal and external degrees of freedom
As discussed in section 4.2, different observers use different interaction Hamiltonians and thus will observe different amounts of correlations (and in different bases) between internal and external degrees of freedom. The key observation here is that a quantum state is defined at a given time on a given space-like surface. The state of a system 'at time t' depends on whose time t is considered. As soon as the described wave-packet has a non-negligible spatial extension, different observers will use different planes of simultaneity and thus will assign different states, simply because they are describing different physical situations. Given a particle in superposition at points x1, x2 at some initial time for observer A, a measurement of entanglement between internal and external degrees of freedom at a given later time for observer A will, for observer B, appear as a measurement in which the two points are probed at different times, as discussed in detail in section 4.1. Thus the same measurement will not be interpreted by B as a measure of the entanglement of the state as described by B at a fixed time. Even though the definition of state, and thus the amount of entanglement, depends on the reference frame, different observers agree on the outcome of any measurement and in particular on the visibility of any interferometric experiment, which only depends on the proper time difference, equation (7).
5. Relevant relativistic and quantum mechanical concepts
While time dilation is responsible for the described effect, low-energy quantum theory and weak gravitational fields are sufficient to derive the time-dilation induced change in interferometeric visibility. Below we discuss the results in light of some basic concepts from relativity and quantum theory.
5.1. Satisfying the equivalence principle
The role of the equivalence principle for the results has been the subject of a number of discussions [4, 6, 29, 36]. Since the predictions are a direct consequence of relativistic time dilation, they automatically satisfy the equivalence principle, which requires that uniformly accelerated reference frames are physically equivalent to those stationary in a homogeneous gravitational field. In particular, all results derived for accelerated observers are equivalent to those derived for stationary observers on Earth in the homogeneous field limit.
Moreover, one can easily see that the weak equivalence principle—requiring that weight and inertia are equal—is satisfied by the Hamiltonian (6). The total rest energy  gives both: inertia and weight. In particular, for the leading-order terms in the Hamiltonian (6), we can see that the gravitational potential energy is
gives both: inertia and weight. In particular, for the leading-order terms in the Hamiltonian (6), we can see that the gravitational potential energy is  (where
(where  is included in
is included in  ), which corresponds to a total weight
), which corresponds to a total weight  . Likewise, inertia is determined from the kinetic energy term: the non-relativistic term
. Likewise, inertia is determined from the kinetic energy term: the non-relativistic term  together with the momentum coupling
together with the momentum coupling  is simply the first-order expansion of
is simply the first-order expansion of  , which means that inertia is also equal to
, which means that inertia is also equal to  . The equivalence principle for matter waves has been studied in several works [45, 46]. Possible quantum violations of the equivalence principle, which would indicate new physics, are discussed in [37] in the context of superpositions of internal energy states.
. The equivalence principle for matter waves has been studied in several works [45, 46]. Possible quantum violations of the equivalence principle, which would indicate new physics, are discussed in [37] in the context of superpositions of internal energy states.
5.2. No dependence on space–time curvature
As is clear from equation (7), the decoherence effect depends on proper time and thus on the metric, not on curvature. A typical example of time dilation is one in which two clocks are held at fixed heights above Earth. This effect is invariably referred to as 'gravitational time dilation'. Similarly, the change in frequency as a light beam travels away from the Earth's surface is commonly known as 'gravitational redshift'. Such effects depend on the g00 component of the metric and not on curvature. In a first-order approximation,  , where
, where  is identified with Newton's potential. In the same way, the decoherence of a particle held in superposition at two heights above Earth depends on g00 and is as much related to gravity as gravitational time dilation or redshift. Note that gravity is not necessary for time dilation: a difference in velocities between superposed paths will also lead to time dilation and thus decoherence. Such a velocity difference can be achieved by considering interferometry in a non-inertial frame such as on a rotating platform [28] or superposing motion of a charged particle at different cyclotron orbits in a magnetic field [27]. Decoherence due to only gravitational effects or only due to kinematic effects as in the examples above are special cases of decoherence due to time dilation.
is identified with Newton's potential. In the same way, the decoherence of a particle held in superposition at two heights above Earth depends on g00 and is as much related to gravity as gravitational time dilation or redshift. Note that gravity is not necessary for time dilation: a difference in velocities between superposed paths will also lead to time dilation and thus decoherence. Such a velocity difference can be achieved by considering interferometry in a non-inertial frame such as on a rotating platform [28] or superposing motion of a charged particle at different cyclotron orbits in a magnetic field [27]. Decoherence due to only gravitational effects or only due to kinematic effects as in the examples above are special cases of decoherence due to time dilation.
Sometimes the viewpoint is advocated that only curvature-related effects are to be considered as gravitational. In this viewpoint the gravitational redshift, gravitational time dilation, falling apples, and also decoherence due to time dilation should not be understood as related to gravity. Such a semantic distinction does not affect the physical predictions of the effects. We note, however, that our analysis applies to arbitrary curved space–times, as long as quantum-field effects can be neglected and the internal structure of the particle only contributes to time-dilation effects. It can be an interesting question what type of experiment in this regime could be used as a probe of space–time curvature or what novel effects may arise that depend only on curvature.
5.3. Describing the effect of time dilation without using quantum field theory
Any physical model, at least any known to date, has a limited range of applicability. For example, quantum field theory in curved space–time cannot describe the back-action of mass-energy on space–time at arbitrary energy scales. In our work, we considered low-energy quantum systems such as atoms, molecules, nanospheres, etc., in a regime in which high-energy quantum field effects, such as particle creation/annihilation, can be neglected. This regime can be well approximated by relativistic quantum mechanics in first quantization. Although it has a limited range of applicability, relativistic quantum mechanics is a well-understood framework that yields powerful predictions, such as corrections to atomic spectra [47, 48]. General relativistic effects can also be included in a first-quantization treatment, for example by including corrections to the non-relativistic Schrödinger equation [42]. Such a treatment neglects the backaction of the probe system onto the metric (but which can also be accounted for in this context, see [33]). The novelty of our analysis is to consider the effects arising from the internal structure of the quantum particle, which can be incorporated in the Klein–Gordon equation by adding the internal energy contribution to the mass.
Of course, it should also be possible to derive the same effects within the framework of quantum field theory in curved space time. An example of such a derivation, based on simple models, was presented in the methods section of our work [3] and in [49].
5.4. The mass superselection rule and relativistic quantum mechanics
The mass superselection rule, raised in [6] in the context of our work, is a result in non-relativistic quantum mechanics and does not apply to the scenario discussed here. It originates from the non-commutativity of the generators of the boost and translation in the Lie algebra of the representation of the Galilei group on the space of solutions to the non-relativistic Schrödinger equation [50, 51]. Specifically, in one space dimension, the Galilei boost generator is  , where
, where  are the position and momentum operators, respectively, and m is the mass of the particle; the generator of translations is
are the position and momentum operators, respectively, and m is the mass of the particle; the generator of translations is  . Thus,
. Thus, ![$[\hat{K},\hat{P}]={\rm{i}}{\hslash }m$](https://content.cld.iop.org/journals/1367-2630/19/2/025011/revision2/njpaa5d92ieqn86.gif) , whereas in the Lie algebra of the Galilei group itself these generators commute. Such a representation is called projective and results here in an additional phase factor proportional to the mass, which in turn leads to the mass-superselection rule: denote by g and
, whereas in the Lie algebra of the Galilei group itself these generators commute. Such a representation is called projective and results here in an additional phase factor proportional to the mass, which in turn leads to the mass-superselection rule: denote by g and  the Galilei group elements of a spatial translation by a and a boost by v, respectively. They satisfy
the Galilei group elements of a spatial translation by a and a boost by v, respectively. They satisfy  (identity element of the Galilei group). However, their representations as operators on the Hilbert space,
(identity element of the Galilei group). However, their representations as operators on the Hilbert space,  and
and  , satisfy
, satisfy  . Applying this sequence to a superposition of states characterized by different masses m and
. Applying this sequence to a superposition of states characterized by different masses m and  results in a relative phase
results in a relative phase  and therefore a different physical state, unless
and therefore a different physical state, unless  . However, this operation should represent identity of the Galilei group and cannot alter physical states. Hence a superposition of states with
. However, this operation should represent identity of the Galilei group and cannot alter physical states. Hence a superposition of states with  is considered unphysical in a Galilei invariant theory and is thus 'forbidden'—this is the original argument of Bargmann [50] behind the superselection rule for the mass.
is considered unphysical in a Galilei invariant theory and is thus 'forbidden'—this is the original argument of Bargmann [50] behind the superselection rule for the mass.
In contrast, representations of the Poincaré group in relativistic quantum theory have the same Lie algebra as the group itself and thus they are unitary—i.e. not projective—representations of the Poincaré group. As a consequence, there is no superselection rule for the mass in relativistic quantum mechanics [52]. So if one does not insist on Galilei invariance, superpositions of states with different mass-energies are not 'forbidden'. (This can also be understood by simply recalling that relativistic quantum mechanics has to incorporate both: mass-energy equivalence of relativity and the superposition principle of quantum theory. As a result superpositions of internal energies must contribute to the mass in precisely the same way as the eigenstates alone.)
6. Aspects of decoherence due to time dilation
In this section we discuss various aspects of the decoherence due to time dilation and compare it to other physical effects.
6.1. Reversibility of decoherence
Whenever a quantum system gets entangled with another system, its coherence is reduced. However, the term 'decoherence' is typically reserved to situations in which the loss of coherence is effectively permanent and difficult to reverse or avoid. It is therefore important to analyze how the entanglement generated by time dilation can give rise to decoherence.
We first discuss the effective irreversibility of the effect due to a large bath. An important point to stress is that any decoherence mechanism stemming from a unitary quantum evolution of a system and its environment is, at least in principle, reversible: a quantum system with discrete energy levels will return infinitely many times arbitrarily close to its initial state [53]. Thus, a system getting entangled with an environment will eventually 'recohere'. The question is how often and for how long the system recoheres, and thus the visibility revives. For the case of decoherence due to time dilation, consider a system with internal composition supported on a subspace spanned by energy eigenstates with energies  . The visibility revives if all the acquired phases differ by a multiple of
. The visibility revives if all the acquired phases differ by a multiple of  . The revival time can be defined as
. The revival time can be defined as  where
where  and
and  , and is simply the lowest common multiple (LCM) of all Tm. For equally spaced internal levels tr is equal to the period of the smallest system's frequency, but in general the LCM is much greater (as in figure 2(d)). Moreover, if the system has at least one pair of incommensurable frequencies, which means
, and is simply the lowest common multiple (LCM) of all Tm. For equally spaced internal levels tr is equal to the period of the smallest system's frequency, but in general the LCM is much greater (as in figure 2(d)). Moreover, if the system has at least one pair of incommensurable frequencies, which means  such that
such that  , the revival time is infinite. Furthermore, the duration of any revival decreases with the number of levels and degrees of freedom (see also figure 2(b) and [28])—and thus systems with larger energy variance not only decohere faster but also recohere for shorter times. Note that, very generally, larger systems recohere after longer times: the recoherence time is exponential in the number of internal levels [54], and revive for a shorter period: since the energy variance also typically grows with the number of internal states (e.g. for thermal states or equally spaced energies). Time dilation can cause loss of coherence for practically infinite time and with negligible duration of recoherences for systems with sufficiently many internal levels and internal degrees of freedom. For a concrete example: a system with Avogadro number of internal modes at room temperature—
, the revival time is infinite. Furthermore, the duration of any revival decreases with the number of levels and degrees of freedom (see also figure 2(b) and [28])—and thus systems with larger energy variance not only decohere faster but also recohere for shorter times. Note that, very generally, larger systems recohere after longer times: the recoherence time is exponential in the number of internal levels [54], and revive for a shorter period: since the energy variance also typically grows with the number of internal states (e.g. for thermal states or equally spaced energies). Time dilation can cause loss of coherence for practically infinite time and with negligible duration of recoherences for systems with sufficiently many internal levels and internal degrees of freedom. For a concrete example: a system with Avogadro number of internal modes at room temperature— ,
,  K—and with the lowest frequency
K—and with the lowest frequency  , in a superposition of locations separated by
, in a superposition of locations separated by  (vertically on Earth) loses visibility to
(vertically on Earth) loses visibility to  after ∼2 s (thus also exhibits revivals of duration ∼4 s) and recoheres after
after ∼2 s (thus also exhibits revivals of duration ∼4 s) and recoheres after  s—the estimated age of the Universe.
s—the estimated age of the Universe.
The second question is whether the decoherence due to time dilation can easily be avoided or reversed through an appropriate control of the external degrees of freedom. Again, this is in principle possible for all decoherence mechanisms discussed in the literature: as long as the system–environment interaction is unitary, and given arbitrary control on both, it is in principle possible to engineer the reverse unitary that recoheres the system. The question is again whether such a reversal becomes impossible for all practical purposes. For the case of time-dilation induced decoherence, one could attempt to reverse the decoherence effect by carefully controlling the interferometric paths. For example, given a system that evolved in superposition of two heights x1, x2 for a time t, it would be sufficient to swap the heights of the amplitudes for an equal time to bring the proper time difference  between the two paths to zero. More generally, no time-dilation induced decoherence would be observed if the total interferometric paths are adjusted to have vanishing proper time difference, see equation (7). What degree of precision would this procedure require? From equation (17) we see that, in order to suppress decoherence, the proper time difference between interferometric paths should be small as compared to
between the two paths to zero. More generally, no time-dilation induced decoherence would be observed if the total interferometric paths are adjusted to have vanishing proper time difference, see equation (7). What degree of precision would this procedure require? From equation (17) we see that, in order to suppress decoherence, the proper time difference between interferometric paths should be small as compared to  . For N thermal harmonic oscillators in the high-temperature limit,
. For N thermal harmonic oscillators in the high-temperature limit,  . Thus, in this limit, for a particle with an Avogadro number of internal modes at room temperature, we need to control the proper time difference to a precision of
. Thus, in this limit, for a particle with an Avogadro number of internal modes at room temperature, we need to control the proper time difference to a precision of  s. For a second-long experiment in Earth's gravitational field,
s. For a second-long experiment in Earth's gravitational field,  , this translates in an atomic-scale precision control of the amplitude's position,
, this translates in an atomic-scale precision control of the amplitude's position,  m. We see that, for increasingly large variance of the internal energy, it becomes practically unfeasible to control the external position of the particle so to avoid time-dilation induced decoherence9
.
m. We see that, for increasingly large variance of the internal energy, it becomes practically unfeasible to control the external position of the particle so to avoid time-dilation induced decoherence9
.
6.2. Gaussian versus exponential decay
The Gaussian decay is a direct consequence of the specific interaction Hamiltonian, equation (6). In all models of decoherence, the system degrees of freedom couple to some degrees of freedom of the bath with an interaction Hamiltonian  . The equation of motion for the system of interest, in the interaction picture and Born approximation, is
. The equation of motion for the system of interest, in the interaction picture and Born approximation, is

where the trace is taken over all bath degrees of freedom. Writing the interaction Hamiltonian as  for some system operator S and bath operator B, the relevant quantities in the above equation are the bath auto-correlation functions in the interaction picture,
for some system operator S and bath operator B, the relevant quantities in the above equation are the bath auto-correlation functions in the interaction picture, ![$\langle B(t)B(t^{\prime} )\rangle ={\mathrm{Tr}}_{B}[B(t)B(t^{\prime} ){\rho }_{B}]$](https://content.cld.iop.org/journals/1367-2630/19/2/025011/revision2/njpaa5d92ieqn117.gif) . In many models of decoherence, these decay very rapidly such that one can approximate
. In many models of decoherence, these decay very rapidly such that one can approximate  . For example, in microscopic models of quantum Brownian motion [55] one has
. For example, in microscopic models of quantum Brownian motion [55] one has  , i.e. coupling to the positions of the bath degrees of freedom with coupling strengths ai, which yields in the high temperature limit10
, i.e. coupling to the positions of the bath degrees of freedom with coupling strengths ai, which yields in the high temperature limit10
 , where m is the mass, T the temperature and γ the damping coefficient of the system.
, where m is the mass, T the temperature and γ the damping coefficient of the system.
In contrast, time dilation causes a coupling to the internal energy of the system,  . Thus the bath auto-correlation functions in the interaction picture remain constant
. Thus the bath auto-correlation functions in the interaction picture remain constant  , where
, where  is the mean internal energy (see also methods in [3]). This decoherence is therefore in the opposite limit than the Markovian models (see also [24] for a discussion of non-Markovianity in this context). A few other models are of similar form, as for example the one by Cucchietti, Paz and Zurek [56] in which a spin couples to the bath spin operators,
is the mean internal energy (see also methods in [3]). This decoherence is therefore in the opposite limit than the Markovian models (see also [24] for a discussion of non-Markovianity in this context). A few other models are of similar form, as for example the one by Cucchietti, Paz and Zurek [56] in which a spin couples to the bath spin operators,  , and which also results in a Gaussian decay of coherence. We note, however, that the Gaussian decay does not persist for all times (see section 6.1 above), and, like the derived Master equation, describes the behavior for the initial loss of coherence.
, and which also results in a Gaussian decay of coherence. We note, however, that the Gaussian decay does not persist for all times (see section 6.1 above), and, like the derived Master equation, describes the behavior for the initial loss of coherence.
6.3. Universality of decoherence due to time dilation
The coupling of position and momentum with the internal energy H0, equation (6), does not depend on the nature of the binding energies and interactions that define H0, which can describe any internal dynamics. This is because the coupling is a consequence of time dilation, which does not depend on the construction of the clock used to measure time. This is captured by the arbitrariness of H0. The experienced proper time τ along the respective world-lines is the relevant quantity, irrespective of the internal mechanisms. Therefore, decoherence due to time dilation is as universal as time dilation itself and can affect any composite quantum system.
6.4. Decoherence and classicality
The so-called transition to classicality is a debated issue in the philosophy and foundations of quantum mechanics [57, 58]. One of the sources of controversy is the very definition of classicality and in which sense the transition is to be understood [5]. One can restrict the discussion to practical questions of why effects such as quantum interference [59] or violations of Bell inequalities [60] are not observed on everyday scales. Decoherence explains this fact by considering interactions with an environment which causes a suppression of coherence in a so-called 'pointer basis', such that typical quantum effects cannot be observed. This follows directly from quantum theory and the study of open quantum systems. A comparison between the strength of decoherence due to time dilation and other decoherence sources can be found in [3, 31, 61].
A further problem often associated with the quantum-to-classical transition is the so-called measurement problem: the questions are why a specific outcome of a quantum measurement occurs and what constitutes a measurement. As an inherently probabilistic theory, quantum mechanics does not provide any means to explain the occurrence of specific outcomes beyond predicting the probability with which they occur. In fact, any theory providing better predictability than quantum mechanics would have to be non-local [62] and contextual [63]. Thus, quantum theory or decoherence cannot answer this aspect of the measurement problem, which is also beyond the scope of our work.
6.5. Time dilation induced decoherence versus gravitationally induced collapse of the wave function
Gravitationally induced collapse models, such as in [7, 8], are based on an inherent modification of quantum theory. It is argued that the superposition principle breaks down if the systems reach a sufficient size. For example, the proposal by Penrose [8] suggests a fundamental collapse time  , where
, where  is the gravitational self energy of the system [64]. The philosophical motivation for this suggestion is the consideration of superpositions of different metrics and how the amplitudes might affect each other. However, the gravitationally induced collapse of the wave function does not follow from quantum theory and is a speculative modification thereof. In contrast, the results in [3] stem fully from within quantum theory and the time dilation originates from an external, fixed background. The dynamics we consider is unitary for the total system—the decoherence takes place due to correlations with an environment (the internal degrees of freedom of the particle), which are induced by time dilation.
is the gravitational self energy of the system [64]. The philosophical motivation for this suggestion is the consideration of superpositions of different metrics and how the amplitudes might affect each other. However, the gravitationally induced collapse of the wave function does not follow from quantum theory and is a speculative modification thereof. In contrast, the results in [3] stem fully from within quantum theory and the time dilation originates from an external, fixed background. The dynamics we consider is unitary for the total system—the decoherence takes place due to correlations with an environment (the internal degrees of freedom of the particle), which are induced by time dilation.
Acknowledgments
We thank Markus Arndt, Markus Aspelmeyer, Angelo Bassi, Lajos Diósi, Fay Dowker, Cisco Gooding, Daniel Greenberger, Eduardo Martin-Martinez, Holger Müller and Carlo Rovelli for discussions. This work was supported by the NSF through a grant to ITAMP, the Society in Science through the Branco Weiss Fellowship administered by the ETH Zürich, the Austrian Science Fund (FWF) through the Special Research Program Foundations and Applications of Quantum Science (FoQuS) and Individual Project (No. 24621), the Australian Research Council Centre of Excellence for Engineered Quantum Systems through grant number CE110001013, by the University of Queensland through UQ Fellowships grant number 2016000089 and by the Templeton World Charity Foundation, grant TWCF 0064/AB38. FC and MZ acknowledge the traditional owners of the land on which the University of Queensland is situated, the Turrbal and Jagera people.
Footnotes
- 6
To fix the particle's world lines it is necessary to apply a suitable potential V(x). While relativistic effects will also play a role in the interaction with the potential, the experienced time dilation is only governed by the proper time of the world lines, irrespective of the nature of the potential that fixes the world lines. As long as the center of mass of the system is well defined, the effect described here does not depend on the potential but only on the proper time, just as for time dilation between two classical systems. More generally, our treatment applies in the regime where the system can be treated as an 'ideal clock', where the external potential does not affect the internal structure of the 'clock'. Whether this idealization applies in practice can depend on the specific experimental design.
- 7
Note that covariance is still guaranteed if an external potential is added to action (4), provided this is expressed in a covariant form, which is always possible in a relativistic treatment.
- 8
In the quantization of higher order terms, an ambiguity arises in the ordering of position and momentum operators. A definition of the Hamiltonian at arbitrary orders can be obtained by expanding the Klein–Gordon equation in curved space–time corresponding to equation (21) to obtain a Schrödinger-like equation with relativistic corrections [42].
- 9
An intereference experiment in free space, i.e. completely in free fall as a whole, would not be affected by gravitational time dilation. However, any relative accelerations between the paths or velocities would induce time dilation, and for large enough systems it will be similarly challenging to avoid or reverse decoherence.
- 10
Note that a thermal bath does not store any information on the system, which is true for any decoherence model including the time dilation model discussed in this manuscript [25].







