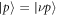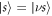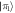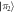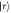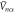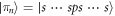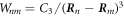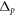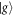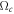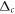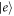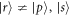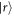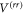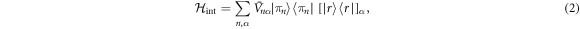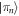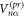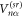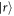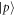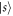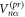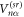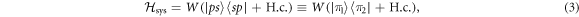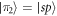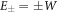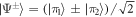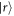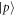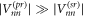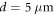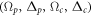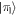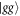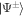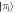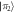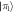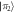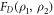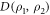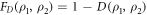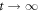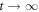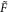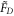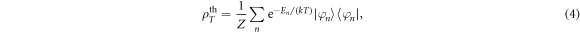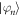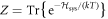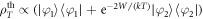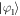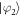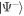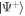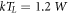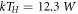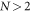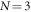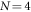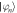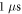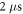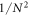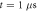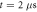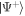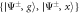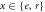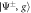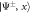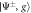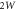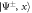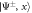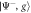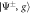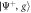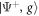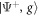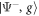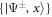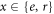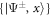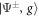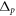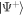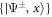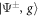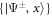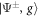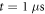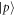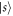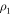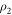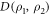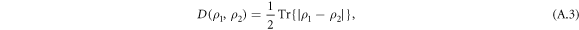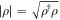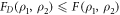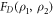Engineering thermal reservoirs for ultracold dipole–dipole-interacting Rydberg atoms

Solving the dynamics of open quantum systems is one important task addressed by quantum simulators [1–4]. The dynamics generated by the environment-couplings of the target system must be reproduced in the simulator [2, 5]. These dynamics depend on the specific details of the system, environment and their coupling. However, there is a common and essential feature required to simulate any system undergoing thermalization: the simulator must evolve to a Boltzmann distribution of its eigenstates. Here, we achieve this goal for the first time in an ultracold Rydberg atomic system. Due to their strong interactions and relative ease to laser-control and position experimentally, Rydberg systems have been proposed for quantum simulation of spin Hamiltonians [6, 7], electron–phonon coupling [8], as well as exciton transport [9–14].

Preparing the desired simulator dynamics is a reservoir engineering [15] problem, which involves design of the environment or its coupling to the system. Reservoir engineering has been proposed and applied for a variety of systems, for example in entanglement generation and protection [16–28], dissipative computation [29], and in preparing effective thermal baths for harmonic oscillators [30] and single atoms [31]. Reservoir engineering has also been applied to the problem of open quantum system simulation [6, 12, 28, 32–40].

In this work, we use reservoir engineering to transform a typically non-thermal environment into a thermal environment with controllable temperature, such that the system relaxes to a corresponding mixture of its eigenstates. Our scheme thus provides the essential feature required for simulation of an open quantum system approaching thermal equilibrium. To accurately simulate a particular target open system, further details of the specific dynamics will need to be engineered; our scheme also offers considerable flexibility that could be used to obtain various kinds of system dynamics.

We consider the setup sketched in figure 1(a). Dipole-coupled Rydberg atoms constitute our system of interest. There are many possibilities for the geometry of the system atoms. Here, as concrete examples, we present results for the dimer and longer equidistant linear chains. The system atoms are prepared in two different Rydberg states. We consider one atom prepared in a Rydberg $| p\rangle =| \nu p\rangle$ state with principal quantum number ν and angular momentum quantum number ${\ell }=1$, and the other atoms prepared in a Rydberg $| s\rangle =| \nu s\rangle$ state with angular momentum ${\ell }=0$. Resonant dipole–dipole interactions lead to coupling between the otherwise degenerate Rydberg states and give rise to collective eigenstates [11, 41].

Zoom In Zoom Out Reset image size

To provide the thermalization of these eigenstates, we use a driven dissipative atomic environment, as shown in figure 1(a), which serves as a highly-tunable environment. In our setup, the steady-state populations of the system eigenstates can be precisely controlled by means of currently-achievable frequencies and intensities of the two lasers driving the environment atoms. We prepare thermal states (i) on a timescale shorter than the system decay timescale and (ii) in a long time limit. While (i) demonstrates dissipative state preparation of thermal states, (ii) can be used to mimic a thermal environment for a quantum simulator. We highlight that the effective temperature scale of the Boltzmann distribution of eigenstates is determined by the system interaction strength rather than the 'ambient' temperature of the ultracold environment.

Our basic setup is the same as in [12] and is also described in detail in the supplementary information, which is available online at stacks.iop.org/NJP/20/013011/mmedia. The system part is given by the Hamiltonian

$$\begin{eqnarray}&&{{ \mathcal H }}_{\mathrm{sys}}=\displaystyle \sum _{n\ne m}{W}_{{nm}}| {\pi }_{n}\rangle \langle {\pi }_{m}| ,\end{eqnarray} \tag{ 1 }$$

where a single $| p\rangle$ excitation localized at atom n is written as $| {\pi }_{n}\rangle =| s\cdots {sps}\cdots s\rangle$. The resonant dipole–dipole interaction ${W}_{{nm}}={C}_{3}/{({{\boldsymbol{R}}}_{n}-{{\boldsymbol{R}}}_{m})}^{3}$, where ${{\boldsymbol{R}}}_{n}$ is the position of atom n and C₃ is a state-dependent coefficient.

The environment for the Rydberg system is provided by laser-driven atoms, which are placed at a distance δ from a given system-atom, such that the vectors along d and δ respectively enclose a right angle. Two laser beams address the environment atoms. The first laser, with Rabi frequency ${{\rm{\Omega }}}_{p}$ and detuning ${{\rm{\Delta }}}_{p}$, couples the ground state $| g\rangle$ of an environment atom to an intermediate state $| e\rangle$. The intermediate state is coupled to a continuum of electromagnetic modes, thereby inducing radiative transitions (spontaneous emission) with decay rate ${{\rm{\Gamma }}}_{p}$ to the ground state of the environment atom. The second laser, with Rabi frequency ${{\rm{\Omega }}}_{c}$ and detuning ${{\rm{\Delta }}}_{c}$, couples the intermediate state $| e\rangle$ to a Rydberg state $| r\rangle \ne | p\rangle ,| s\rangle$.

The Rydberg states $| r\rangle$ of the environment atoms introduce interactions both between the environment atoms and between the environment atoms and system atoms. The environment atoms interact with each other via van der Waals interaction ${V}^{({rr})}$. The interactions between environment and system atoms are state-dependent,

$$\begin{eqnarray}&&{{ \mathcal H }}_{\mathrm{int}}=\displaystyle \sum _{n,\alpha }{\bar{V}}_{n\alpha }| {\pi }_{n}\rangle \langle {\pi }_{n}| {[| r\rangle \langle r| ]}_{\alpha },\end{eqnarray} \tag{ 2 }$$

where ${\bar{V}}_{n\alpha }={V}_{n\alpha }^{({pr})}+{\sum }_{m\ne n}{V}_{m\alpha }^{({sr})}$ denotes the overall interaction of a specific environment atom α with the entire system if the latter is in the state $| {\pi }_{n}\rangle$. Here, ${V}_{n\alpha }^{({pr})}$ (${V}_{n\alpha }^{({sr})}$) indicates the interaction between the $| r\rangle$ state of environment atom α with a $| p\rangle$ ($| s\rangle$) excitation at system atom n. Due to their distance-dependence, the interactions ${V}_{n\alpha }^{({pr})}$ and ${V}_{n\alpha }^{({sr})}$ increase drastically with decreasing distance and are therefore strongest for adjacent environment and system atoms, i.e., $\alpha =n$.

We emphasize that the tunability of the environment arises through its composition of a finite part, the laser-driven three-level atoms, and an infinite part, the photon bath. By tuning the parameters of the lasers addressing the environment atoms, the dynamics within the finite part can be controlled. This in turn affects the system dynamics.

We now exemplify the relevant properties of our setup for a Rydberg dimer, i.e., two Rydberg atoms as shown in figure 1(b). The Hamiltonian (1) now reads:

$$\begin{eqnarray}&&{{ \mathcal H }}_{\mathrm{sys}}=W(| {ps}\rangle \langle {sp}| +{\rm{H}}.{\rm{c}}.)\equiv W(| {\pi }_{1}\rangle \langle {\pi }_{2}| +{\rm{H}}.{\rm{c}}.),\end{eqnarray} \tag{ 3 }$$

where H.c. denotes the Hermitian conjugate and $| {\pi }_{1}\rangle =| {ps}\rangle$ ($| {\pi }_{2}\rangle =| {sp}\rangle$). We will later be concerned with the eigenvalues of this Hamiltonian, given by ${E}_{\pm }=\pm W$, and the corresponding Bell eigenstates $| {{\rm{\Psi }}}^{\pm }\rangle =(| {\pi }_{1}\rangle \pm | {\pi }_{2}\rangle )/\sqrt{2}$. For simplicity, we do not include the finite lifetime of the system in our calculations.

The resulting level scheme for a Rydberg dimer is shown in figure 1(c). For state engineering to be feasible, it is essential that the interaction between an environment Rydberg state $| r\rangle$ and the states $| p\rangle$ and $| s\rangle$ of the adjacent system atom are different, e.g. obeying $| {V}_{{nn}}^{({pr})}| \gg | {V}_{{nn}}^{({sr})}|$. The numerical values of the interactions are the same as in [12] and are detailed in the supplementary information. In the following, we choose the environment-atom geometry such that $d=5\,\mu {\rm{m}}$ and δ = 2 μm.

For each state that we prepare, we numerically optimize the laser parameters $({{\rm{\Omega }}}_{p},{{\rm{\Delta }}}_{p},{{\rm{\Omega }}}_{c},{{\rm{\Delta }}}_{c})$ for the fixed geometry. Note that the optimized laser parameters are independent of the initial state of system or environment. We thus use a system (environment) state that is easy to access experimentally in our numerical simulations, given by $| {\pi }_{1}\rangle$ ($| {gg}\rangle$). The physical mechanism for the state preparation is described in section 4.1.

To illustrate the control provided by the finite environment, we first prepare the Bell eigenstates $| {{\rm{\Psi }}}^{\pm }\rangle$ of the system Hamiltonian for the Rydberg dimer (3). We subsequently demonstrate reservoir-engineered thermalization in our system.

3.1. Eigenstate preparation

In figure 2 we illustrate the preparation of the anti-symmetric (a) as well as the symmetric (b) Bell state. The marked revival feature in the population dynamics is absent in the dynamics of the eigenstate populations, indicating that the eigenstates can indeed be selectively addressed by the dissipative environment.

Zoom In Zoom Out Reset image size

To assess the difference between the target density matrix, in this case the projector on the appropriate Bell state, and the density matrix obtained after numerical propagation, we employ two often-adopted distance measures (see [42, 43]). The first measure is the fidelity $F({\rho }_{1},{\rho }_{2})$, and the second measure ${F}_{D}({\rho }_{1},{\rho }_{2})$ is related to trace distance $D({\rho }_{1},{\rho }_{2})$ via ${F}_{D}({\rho }_{1},{\rho }_{2})=1-D({\rho }_{1},{\rho }_{2})$. Details are given in the appendix. To illustrate the different timescales on which steady-state preparation is feasible, we evaluate the two distance measures F and F_D at $t=1\,\mu {\rm{s}}$ and $t\to \infty$ respectively, denoting the $t\to \infty$ case by $\tilde{F}$ and ${\tilde{F}}_{D}$. As shown in figure 2 and provided numerically in the supplementary information, high-fidelity preparation can be achieved on a timescale of about 1 μs, which is much shorter than the lifetime of the chosen dimer states, which is approximately 56 μs [44].

3.2. Thermal state preparation

The main result of this work is that we can prepare thermal mixtures of the system eigenstates [45]

$$\begin{eqnarray}&&{\rho }_{T}^{\mathrm{th}}=\displaystyle \frac{1}{Z}\displaystyle \sum _{n}{{\rm{e}}}^{-{{E}}_{n}/({kT})}| {\varphi }_{n}\rangle \langle {\varphi }_{n}| ,\end{eqnarray} \tag{ 4 }$$

where $| {\varphi }_{n}\rangle$ and E_n are the eigenstates and eigenenergies of ${{ \mathcal H }}_{\mathrm{sys}}$, respectively. The Boltzmann constant is denoted by k, the temperature by T, and $Z=\mathrm{Tr}\{{{\rm{e}}}^{-{{ \mathcal H }}_{\mathrm{sys}}/({kT})}\}$. We emphasize that T is not the ambient temperature of the environment atoms, which is typically ∼μK. Note that the relevant energy scale providing the temperature scale is the resonant dipole–dipole interaction W. For a dimer, the two system eigenstates are separated in energy by $2W$, such that ${\rho }_{T}^{\mathrm{th}}\propto (| {\varphi }_{1}\rangle \langle {\varphi }_{1}| +{{\rm{e}}}^{-2W/({kT})}| {\varphi }_{2}\rangle \langle {\varphi }_{2}| )$, where $| {\varphi }_{1}\rangle$ and $| {\varphi }_{2}\rangle$ are the dimer eigenstates $| {{\rm{\Psi }}}^{-}\rangle$ and $| {{\rm{\Psi }}}^{+}\rangle$, respectively. To illustrate the versatility of the scheme we demonstrate low and high temperature mixtures, given by ${{kT}}_{L}=1.2\,W$ and ${{kT}}_{H}=12.3\,W$ respectively. The numerical values are chosen such that T_L yields strong asymmetries in the eigenstate populations while T_H yields similar occupations of the eigenstates.

For a Rydberg dimer, the preparation of thermal states with temperature T_L (c) and T_H (d) is shown in figure 2, using exemplary laser parameter sets. Both states can be prepared with high fidelity.

Dissipative state-preparation is not limited to a Rydberg dimer. To demonstrate this, we extend the setup shown in figure 1(b) by placing $N\gt 2$ system atoms on an equidistant, one-dimensional lattice (lattice constant d). The environment atoms are placed on a copy of this lattice, shifted by the distance δ orthogonal to the system lattice. In figure 3 we show the preparation of thermal states with temperatures T_L and T_H for a Rydberg trimer ($N=3$ system atoms) as well as a tetramer ($N=4$ system atoms) using exemplary laser parameter sets. In both cases, the thermal states can be prepared with high fidelity (see supplementary information).

Zoom In Zoom Out Reset image size

Numerical optimization for large systems is impeded due to the exponential increase of Hilbert space size with environment atoms¹ . For this reason, we have simulated up to 6 system and environment atoms to verify the scalability of our approach, where for every system size the laser parameters are fixed to those optimized for $N=4$. We evaluated F_D after $1\,\mu {\rm{s}}$ and $2\,\mu {\rm{s}}$ for thermal state preparation with temperatures T_H and T_L, respectively. This is shown in figure 4. We find a weak dependence of F_D on system size, and we thus expect our preparation scheme to be applicable to even larger system sizes. Optimization for each chain length N is expected to improve the corresponding state preparation. Note, however, that state-preparation at short timescales becomes more difficult for larger system sizes. In particular, for constant atom spacing, the energy differences between the system eigenenergies decrease with increasing system size as $1/{N}^{2}$. Larger timescales are thus required for distinctive dynamics for individual eigenstates to emerge as needed for the preparation of low-temperature thermal states.

Zoom In Zoom Out Reset image size

We have demonstrated thermal state preparation with varying temperature and system size, which provides access to a broad range of open system dynamics for quantum simulation with ultracold atoms. We now explore the underlying mechanism for the thermalization dynamics, which highlights the flexibility in system dynamics provided by a controllable, finite environment. We also consider the robustness to variations in the system parameters.

4.1. Physical mechanism

The underlying mechanism for preparation of both the Bell and thermal steady states can be traced back to the appearance of quasi-resonances. This is illustrated most clearly for the case of Bell state preparation: to prepare a specific Bell state, we want to ensure that (i) there is negligible population transfer out of this target state, while (ii) population is transfered from the non-target Bell state to the target state.

In the following we discuss exemplarily for the preparation of the $| {{\rm{\Psi }}}^{+}\rangle$ state how the above requirements (i) and (ii) can be fulfilled. To simplify the discussion we consider the smallest system that allows dissipative state preparation, i.e., a Rydberg dimer with a single environment atom (see figure 5(b)).

Zoom In Zoom Out Reset image size

For the preparation of the $| {{\rm{\Psi }}}^{+}\rangle$ state, a convenient choice of the target system-environment state is the product state $| {{\rm{\Psi }}}^{+},g\rangle$. This state, which contains the desired system state, does not lose population due to spontaneous emission. To guarantee that our target state will emerge as a steady state in the long-time dynamics, we further ensure that negligible population transfer out of this state occurs in the coherent evolution. This can be done by energetically detuning our target state $| {{\rm{\Psi }}}^{+},g\rangle$ from all other states to which it couples, thereby satisfying condition (i). The second condition (ii) can be met by engineering a quasi-resonance between the non-target Bell state $| {{\rm{\Psi }}}^{-},g\rangle$ and a state of the $\{| {{\rm{\Psi }}}^{\pm },x\rangle \}$ manifold, with $x\in \{e,r\}$. That way, population is transferred from the non-target state to the $\{| {{\rm{\Psi }}}^{\pm },x\rangle \}$ manifold, from where it can decay into the $| {{\rm{\Psi }}}^{\pm },g\rangle$ states. This engineering can be done by choosing appropriate laser parameters; in particular an appropriate detuning ${{\rm{\Delta }}}_{p}$. Details on how the appropriate parameters can be obtained analytically are provided in the supplementary material. There, it is also demonstrated that this choice of parameters leads to high state-preparation fidelities.

In figure 5 we present a sketch of the energy levels of the states involved in the preparation of the $| {{\rm{\Psi }}}^{+}\rangle$ state described above, illustrating both the detuning of the target $| {{\rm{\Psi }}}^{+},g\rangle$ state from the coherent dynamics and the quasi-resonance between non-target $| {{\rm{\Psi }}}^{-},g\rangle$ state and the $\{| {{\rm{\Psi }}}^{\pm },x\rangle \}$ manifold. We note that preparation of the target state can be achieved using different sets of laser parameters. These parameters can lead to more complicated schemes than that depicted in figure 5. The various options of effective parameters show the great flexibility of our setup, and also highlight the usefulness of numerical optimization in finding effective parameters, since the relationship between parameters and state preparation performance is nontrivial.

For thermal state preparation, complete isolation of one target state is no longer desirable. Since the target state is now a mixture of the system eigenstates, we prepare couplings of varying strength from both $| {{\rm{\Psi }}}^{\pm },g\rangle$ states to the subspace spanned by the states $\{| {{\rm{\Psi }}}^{\pm },x\rangle \}$. Perhaps the simplest case involves coupling a single state in this subspace to both $| {{\rm{\Psi }}}^{\pm },g\rangle$ states. Then the relative energies of the states can be controlled to provide the requisite thermal populations.

For more system atoms, there are a larger number of states, and necessarily more complex contributions due to more couplings, which complicate analytical considerations. Nevertheless, this quasi-resonance picture can still be used to describe the (multiple) involved processes. The precise parameter contributions in this case we determine via numerical optimization, to provide the desired balance of population gain/loss of the system eigenstates for state preparation even for larger systems, as we have demonstrated.

4.2. Robustness

We have shown that just a few laser-driven atoms already realize a tunable environment enabling tailored dissipative state preparation in a Rydberg system. In particular, thermal states with temperatures vastly different from the temperature of the ultracold atomic environment can be prepared with high fidelity, using only the laser frequencies and intensities driving the environment atoms as control parameters. This provides an essential element for quantum simulation of a particular target open system. For accurate quantum simulation, further details of the specific dynamics will need to be engineered. Our scheme offers considerable flexibility. For instance, the dynamics towards thermal equilibrium depends on the chosen laser parameters and inter-atomic distances. Examples of different parameter choices leading to different thermalization dynamics towards the same thermal state (with high preparation fidelity) are shown in figure 1 of the supplementary information.

The relationship between the laser parameters and the effective temperature of the final thermal state is non-trivial, and further investigation would support the application of this method to ultracold systems. Detection of the spontaneous decay events in the environment atoms, which can herald state preparation, could also give further flexibility to our state-preparation scheme, and provide conditional enhancement of the state fidelity [26].

We note that scalability of the Rydberg system to larger sizes is limited by the radiative lifetimes of the Rydberg $| p\rangle$ and $| s\rangle$ states. An experimental realization in this case would require conditioning on a non-decayed system. Using higher-lying Rydberg states with longer lifetimes could diminish the demands on the experiment.

We applied our method of introducing environmental Rydberg atoms to several different Rydberg system Hamiltonians (with atomic arrangements that are different from a linear chain and that have a different eigenenergy structure). Our findings were consistent with the detailed case in the manuscript: thermal states were effectively prepared in the steady state, with trace distance measures close to unity. This indicates that our proposal is applicable for system Hamiltonians more generic than the ones discussed in this manuscript, however it is an open question whether there are criteria which these Hamiltonians have to satisfy such that our method can be successfully applied.

Financial support from the German Academic Exchange Service, DAAD, (project 57274372) is gratefully acknowledged.

Here we detail the two distance measures employed in the main text. The first measure is the fidelity. The fidelity between two density matrices ${\rho }_{1}$ and ${\rho }_{2}$ is defined as [42]

$$\begin{eqnarray}&&F({\rho }_{1},{\rho }_{2})=\mathrm{Tr}\{\sqrt{\sqrt{{\rho }_{1}}{\rho }_{2}\sqrt{{\rho }_{1}}}\},\end{eqnarray} \tag{ A.1 }$$

and can be interpreted a generalized measure of the overlap between two quantum states [43].

The second measure is related to the trace distance via

$$\begin{eqnarray}&&{F}_{D}({\rho }_{1},{\rho }_{2})=1-D({\rho }_{1},{\rho }_{2}).\end{eqnarray} \tag{ A.2 }$$

The trace distance $D({\rho }_{1},{\rho }_{2})$, which can be interpreted as a measure of state distinguishability, is defined as

$$\begin{eqnarray}&&D({\rho }_{1},{\rho }_{2})=\displaystyle \frac{1}{2}\mathrm{Tr}\{| {\rho }_{1}-{\rho }_{2}| \},\end{eqnarray} \tag{ A.3 }$$

with $| \rho | =\sqrt{{\rho }^{\dagger }\rho }$. From the relation $1-F({\rho }_{1},{\rho }_{2})\leqslant D({\rho }_{1},{\rho }_{2})$ [42] it follows that ${F}_{D}({\rho }_{1},{\rho }_{2})\leqslant F({\rho }_{1},{\rho }_{2})$, which implies that ${F}_{D}({\rho }_{1},{\rho }_{2})$ is a more conservative measure.