Abstract
We investigate the emergence of a time crystal (TC) in a driven dissipative many-body spin array. In this system the interplay between incoherent spin pumping and collective emission stabilizes a synchronized non-equilibrium steady state which in the thermodynamic limit features a self-generated time-periodic pattern imposed by collective elastic interactions. In contrast to prior realizations where the time symmetry is already broken by an external drive, here it is only spontaneously broken by the elastic exchange interactions and manifest in the two-time correlation spectrum. Employing a combination of exact numerical calculations and a second-order cumulant expansion, we investigate the impact of many-body correlations on the TC formation and establish a connection between the regime where it is stable and where the system features a slow growth rate of the mutual information. This observation allows us to conclude that the TC studied here is an emergent semi-classical out-of-equilibrium state of matter. We also confirm the rigidity of the TC to single-particle dephasing. Finally, we discuss an experimental implementation using long lived dipoles in an optical cavity.
Export citation and abstract BibTeX RIS
Introduction
Experimental progress in the control and preparation of quantum cold gases [1] has opened a new era in which non-equilibrium phenomena have a central role. In particular, time crystals (TCs) [2–15]—phases of quantum matter which spontaneously break time translational invariance and which can only exist in out-of-equilibrium systems [16]—have recently attracted significant attention. A system hosting a crystalline time phase should be many-body and exhibit an order parameter, 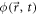 , whose unequal time correlation function approaches, in the thermodynamic limit, a non-trivial periodic, oscillating function of time [16]:
, whose unequal time correlation function approaches, in the thermodynamic limit, a non-trivial periodic, oscillating function of time [16]:  , at sufficiently large distances
, at sufficiently large distances 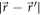 . Such behavior must be robust to imperfections of the system parameters or external perturbations.
. Such behavior must be robust to imperfections of the system parameters or external perturbations.
So far TCs have been experimentally realized [17, 18] in periodically driven, interacting quantum many-body systems with spatial disorder, also known as Floquet TCs [7–12]. Typically, disorder provokes the onset of a many-body localized phase or a pre-thermal state [7, 16, 19–24] where heating towards infinite temperature is suppressed [25–28], and time-resolved observables can react to the periodic drive with a dynamical entrainment at a frequency which is a subharmonic of the one imposed by the external drive. Besides those implementations, which directly break discrete time symmetry, there are other proposals of TCs that break continuous time symmetry [29–31]. However, to our knowledge, there has been no experimental observation of a continuous TC in a quantum many-body system.
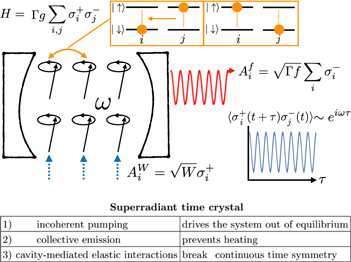
In this work, we propose a paradigm shift in the concept of TCs, which can lead to the first experimental observation of continuous time symmetry breaking, by considering an incoherently driven array of long lived dipoles in a cavity which are subject to collective dissipative decay (superradiance) and elastic long range interactions (see figure 1). Our scheme is similar in spirit to recently proposed quantum TCs with dissipation [14, 32–34] and connected to the emergence of a time-periodic steady state in the thermodynamic limit of an open quantum system. However, the key difference is that by applying incoherent pumping instead of a coherent, periodic drive we do not impose an external frequency which explicitly breaks the time translational symmetry ab initio; rather, the latter is only spontaneously broken by the subtle interplay between collective interactions and driving processes, and accordingly our proposal belongs to the class of TCs which spontaneously break a continuous time translational symmetry. Moreover, the incoherent drive allows for the population of a much larger Hilbert space compared to the fully symmetric Dicke manifold.
Figure 1. An ensemble of N spin 1/2 particles pumped at rate W, experiencing collective emission at rate ∝f Γ and collective spin-exchange interactions (orange), ∝gΓ, form the basis of the superradiant TC. The elastic interactions imprint collective spin oscillations at frequency ω spontaneously breaking the time translation symmetry (manifested as persistent oscillations in the unequal time spin–spin correlation function in the thermodynamic limit).
Download figure:
Standard image High-resolution imageWithin our framework, collective emission prevents unwanted heating and fulfills the role of disorder-induced localization in the Floquet TC (see figure 1). The balance of pumping and dissipation leads to the stabilization of a non-equilibrium synchronized steady-state [35–37] and allows for the formation of a TC that is robust to imperfections or environmental disturbances in the presence of finite but moderate elastic interactions. While the TC exists only when elastic interactions are present, we also find that if they are too strong they can destroy the periodic order. The TC thus only exists within a finite window of interaction strengths with a width which we show grows as the square-root of the particle number. Moreover, in our system the TC emerges for any arbitrary initial state, since our driven dissipative system loses memory of the initial conditions. This is in sharp contrast with closed Hamiltonian systems, where energy conservation is always required and is always reflected in the steady-state. The melting of the TC can be understood from the population of low-lying eigenvectors of the Liouvillian operator that have a finite negative real component: we find that these eigenvalues can be linked to the growth of mutual information in the transient dynamics.
Model
We consider an ensemble of N spin-1/2 particles, whose evolution is described by a master equation for the density matrix 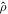 ,
,
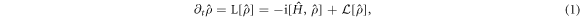
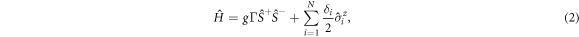
where 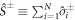 and
and  are the Pauli matrices (a = x, y, z) acting on spin i = 1, ..., N. The first term in
are the Pauli matrices (a = x, y, z) acting on spin i = 1, ..., N. The first term in 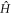 describes a collective spin-exchange interaction, whilst the second describes a static disordered magnetic field along the
describes a collective spin-exchange interaction, whilst the second describes a static disordered magnetic field along the  -direction. Notice we avoid normalization of the interaction term by N to model relevant experimental implementations of our system [38, 39]. For simplicity, but without loss of generality, we assume the δi's are distributed according to a Lorentzian of width Δ and zero mean. The dissipator
-direction. Notice we avoid normalization of the interaction term by N to model relevant experimental implementations of our system [38, 39]. For simplicity, but without loss of generality, we assume the δi's are distributed according to a Lorentzian of width Δ and zero mean. The dissipator ![${ \mathcal L }[\hat{\rho }]={{ \mathcal L }}^{W}[\hat{\rho }]+{{ \mathcal L }}^{f}[\hat{\rho }]$](https://content.cld.iop.org/journals/1367-2630/20/12/123003/revision2/njpaaf18bieqn9.gif) encodes two channels: local, incoherent pumping described by
encodes two channels: local, incoherent pumping described by ![${{ \mathcal L }}^{W}[\hat{\rho }]\equiv {\sum }_{i}{\hat{A}}_{i}^{W}\hat{\rho }{\hat{A}}_{i}^{W\dagger }$](https://content.cld.iop.org/journals/1367-2630/20/12/123003/revision2/njpaaf18bieqn10.gif)
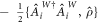 with
with  , and collective emission described by
, and collective emission described by ![${{ \mathcal L }}^{f}[\hat{\rho }]\equiv {\hat{A}}^{f}\hat{\rho }{\hat{A}}^{f\dagger }$](https://content.cld.iop.org/journals/1367-2630/20/12/123003/revision2/njpaaf18bieqn13.gif)
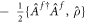 with
with  . The parameter Γ sets the scale of the spin–spin interactions, while g and f are dimensionless parameters characterizing the relative strength of their corresponding elastic and dissipative part, respectively. The use of a master equation [40, 41] to deal with the dissipative processes is extremely accurate for the experimental systems discussed below [38, 42]. The incoherent nature of the pumping preserves the U(1) phase symmetry of the dynamics (which can be seen by the invariance of
. The parameter Γ sets the scale of the spin–spin interactions, while g and f are dimensionless parameters characterizing the relative strength of their corresponding elastic and dissipative part, respectively. The use of a master equation [40, 41] to deal with the dissipative processes is extremely accurate for the experimental systems discussed below [38, 42]. The incoherent nature of the pumping preserves the U(1) phase symmetry of the dynamics (which can be seen by the invariance of ![${ \mathcal L }[\hat{\rho }]$](https://content.cld.iop.org/journals/1367-2630/20/12/123003/revision2/njpaaf18bieqn16.gif) under the transformation
under the transformation 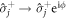 ). In fact, in the steady state the condition
). In fact, in the steady state the condition 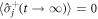 , is always satisfied. Moreover, the incoherent pumping allows coupling between states with different total S, with S(S + 1) the eigenvalues of the
, is always satisfied. Moreover, the incoherent pumping allows coupling between states with different total S, with S(S + 1) the eigenvalues of the 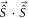 operator, and thus the dynamics is not restricted to the collective S = N/2 manifold.
operator, and thus the dynamics is not restricted to the collective S = N/2 manifold.
Mean-field analysis
We start with a simple mean-field analysis which illustrates how synchronization emerges in a dissipative setting. It assumes that the many-body density matrix can be written as a tensor product of single-spin density matrices and thus neglects spin–spin correlations. This is equivalent to a description of the system in terms of N Bloch vectors, 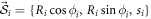 , where Ri represents the length of the Bloch vector projected into the xy-plane, ϕi is the azimuthal angle measured from the positive x-axis, si is the z-component, and i = 1, ..., N. In the mean-field treatment the effect of the elastic and dissipative interactions is to generate a self-adjusting effective complex magnetic field identically experienced by each spin in the ensemble due to interactions with the other spins. The corresponding nonlinear Bloch equations are presented in the SM7
. Here, we focus on the dynamics of the azimuthal phases,
, where Ri represents the length of the Bloch vector projected into the xy-plane, ϕi is the azimuthal angle measured from the positive x-axis, si is the z-component, and i = 1, ..., N. In the mean-field treatment the effect of the elastic and dissipative interactions is to generate a self-adjusting effective complex magnetic field identically experienced by each spin in the ensemble due to interactions with the other spins. The corresponding nonlinear Bloch equations are presented in the SM7
. Here, we focus on the dynamics of the azimuthal phases,

with 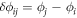 . From direct inspection, we see that in equation (3) the term proportional to f can be identified with a similar term in the Kuramoto model [43], the iconic model used to describe the emergence of phase synchronization in classical nonlinear oscillators. For synchronization to occur, the coupling strength per oscillator, here proportional to f Γsi > 0, must be positive and large enough to compensate for the dephasing generated by the different single particle frequencies. This condition is only possible in the presence of incoherent pumping and thus intrinsic to our setup since a coherent drive does not lead to population inversion in the steady-state [44, 45]. The term proportional to g, arising from the real part of the effective magnetic field, also present in the Kuramoto–Sakaguchi model [46], is responsible for imprinting a collective spin rotation on the non-equilibrium steady state. The effective field not only induces a net collective precession but also favors spin alignment and self-rephasing against the depolarization induced by the inhomogeneous field as theoretically and experimentally demonstrated in prior work [38, 47–52]. Therefore, both f and g are responsible for the rigidity of the TC.
. From direct inspection, we see that in equation (3) the term proportional to f can be identified with a similar term in the Kuramoto model [43], the iconic model used to describe the emergence of phase synchronization in classical nonlinear oscillators. For synchronization to occur, the coupling strength per oscillator, here proportional to f Γsi > 0, must be positive and large enough to compensate for the dephasing generated by the different single particle frequencies. This condition is only possible in the presence of incoherent pumping and thus intrinsic to our setup since a coherent drive does not lead to population inversion in the steady-state [44, 45]. The term proportional to g, arising from the real part of the effective magnetic field, also present in the Kuramoto–Sakaguchi model [46], is responsible for imprinting a collective spin rotation on the non-equilibrium steady state. The effective field not only induces a net collective precession but also favors spin alignment and self-rephasing against the depolarization induced by the inhomogeneous field as theoretically and experimentally demonstrated in prior work [38, 47–52]. Therefore, both f and g are responsible for the rigidity of the TC.
Diagnosis of the TC regime at the mean-field level proceeds by assuming the existence of a synchronized solution of the mean-field equations, namely setting  to zero and determining self-consistently the associated frequency which governs the collective oscillatory dynamics. Later we will restore the detunings and show robustness of the TC to those imperfections. We define the normalized collective order parameter
to zero and determining self-consistently the associated frequency which governs the collective oscillatory dynamics. Later we will restore the detunings and show robustness of the TC to those imperfections. We define the normalized collective order parameter 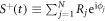 , and assume the following scaling form S+(t)/N =
, and assume the following scaling form S+(t)/N = 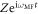 , looking for a solution of the equations of motion which is stationary in the frame co-rotating at the angular frequency ωMF. This mean-field solution can feature collective oscillations in the order parameter S+(t) breaking the U(1)-symmetry of the microscopic dynamics (equation (1)). This is not the case in the exact solution that must preserve the U(1)-symmetry,
, looking for a solution of the equations of motion which is stationary in the frame co-rotating at the angular frequency ωMF. This mean-field solution can feature collective oscillations in the order parameter S+(t) breaking the U(1)-symmetry of the microscopic dynamics (equation (1)). This is not the case in the exact solution that must preserve the U(1)-symmetry, 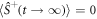 , where the long time limit is taken for a fixed N.
, where the long time limit is taken for a fixed N.
The system synchronizes when Z acquires a positive real value, which is self-consistently determined from the system's parameters [35, 37]. For W < f Γ the mean-field equations do not admit a synchronized solution for Z, as single particle emission dominates the dynamics and the system depolarizes completely. The same occurs if W > f N Γ, since in this regime pumping dominates, heating the system into a trivial incoherent state fully polarized along the 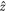 -direction; however, for N > 8 there always exists a finite window of pumping values for which the system enters a synchronized phase, with non-vanishing order parameter featuring collective, synchronous, oscillatory dynamics at the angular frequency ωMF. There exists an optimal pumping rate, Wopt = f N Γ/2 (assuming
-direction; however, for N > 8 there always exists a finite window of pumping values for which the system enters a synchronized phase, with non-vanishing order parameter featuring collective, synchronous, oscillatory dynamics at the angular frequency ωMF. There exists an optimal pumping rate, Wopt = f N Γ/2 (assuming 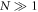 ), for which the magnitude of the order parameter reaches a maximum value,
), for which the magnitude of the order parameter reaches a maximum value, 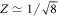 (see SM (see footnote 6)). While Z is found to be independent of g, ωMF is proportional to g and approaches
(see SM (see footnote 6)). While Z is found to be independent of g, ωMF is proportional to g and approaches 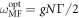 at optimal pumping. The rigidity of this frequency will be discussed below.
at optimal pumping. The rigidity of this frequency will be discussed below.
Quantum model
We now extend our understanding of the formation of the TC beyond the mean-field approximation. Specifically, we study the order parameter for the TC given in terms of the two-time correlation function,

Our analysis is based on an efficient exact numerical solution of the master equation (equation (1)) that uses the spin permutation symmetry to drastically improve the exponential scaling of the Liouville space from 4N to 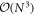 [53–55].
[53–55]. 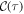 is computed via the linear quantum regression theorem [41],
is computed via the linear quantum regression theorem [41], ![$\langle {\hat{\sigma }}_{i}^{+}(t+\tau ){\hat{\sigma }}_{j}^{-}(t)\rangle \,=\mathrm{Tr}[{\hat{\sigma }}_{i}^{+}{{\rm{e}}}^{{\rm{L}}\tau }[{\hat{\sigma }}_{j}^{-}\hat{\rho }(t)]]$](https://content.cld.iop.org/journals/1367-2630/20/12/123003/revision2/njpaaf18bieqn32.gif) , which is exact for the case of a master equation.
, which is exact for the case of a master equation.
The square root of the equal time correlator, 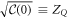 , corresponds to the quantum analog of Z. In close agreement with the mean-field solution, ZQ is found to be nonzero within a window of pumping W where the system synchronizes, and reaches a maximum value,
, corresponds to the quantum analog of Z. In close agreement with the mean-field solution, ZQ is found to be nonzero within a window of pumping W where the system synchronizes, and reaches a maximum value, 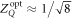 , almost independently of g at Wopt, when the system is maximally synchronized (see SM (see footnote 6)). On the other hand
, almost independently of g at Wopt, when the system is maximally synchronized (see SM (see footnote 6)). On the other hand 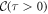 is highly dependent on g. At optimal pumping, large N and finite but moderate interactions,
is highly dependent on g. At optimal pumping, large N and finite but moderate interactions, 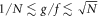 , the order parameter
, the order parameter 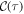 oscillates at the mean-field angular frequency
oscillates at the mean-field angular frequency 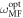 . The oscillations slowly decay but appear to become persistent in the thermodynamic limit, thus signaling the emergence of a TC. In other words, in units of the TC periodicity, the decay time goes to infinity in the thermodynamic limit. Figure 2(a) illustrates this aspect, where
. The oscillations slowly decay but appear to become persistent in the thermodynamic limit, thus signaling the emergence of a TC. In other words, in units of the TC periodicity, the decay time goes to infinity in the thermodynamic limit. Figure 2(a) illustrates this aspect, where 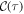 is plotted as a function of the characteristic time η ≡ f N Γτ for N = 10, 50 and N = 100.
is plotted as a function of the characteristic time η ≡ f N Γτ for N = 10, 50 and N = 100.
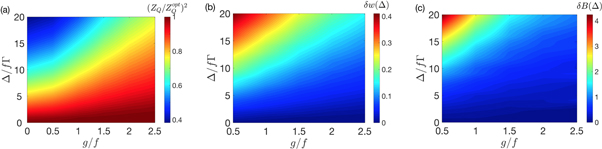
Figure 2. (a) Real part of 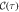 as a function of the characteristic time η ≡ fN Γ τ at optimal pumping and g/f = 1/2 for a system of N = 10 (blue), N = 50 (red), and N = 100 (orange) spins along with the finite size scaling prediction in the thermodynamic limit (purple). (b) Extracted ratio of the absolute value of
as a function of the characteristic time η ≡ fN Γ τ at optimal pumping and g/f = 1/2 for a system of N = 10 (blue), N = 50 (red), and N = 100 (orange) spins along with the finite size scaling prediction in the thermodynamic limit (purple). (b) Extracted ratio of the absolute value of 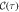 angular frequency
angular frequency 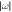 over its spectral width B (see SM (see footnote 6)) versus system size N and interaction coupling g/f. We also show a frequency contour corresponding to
over its spectral width B (see SM (see footnote 6)) versus system size N and interaction coupling g/f. We also show a frequency contour corresponding to  (purple) and a contour of mutual information growth corresponding to
(purple) and a contour of mutual information growth corresponding to 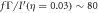 (yellow). (c) Growth rate of two-particle mutual information at short characteristic times (here we set η = 0.03) starting from a maximally coherent array
(yellow). (c) Growth rate of two-particle mutual information at short characteristic times (here we set η = 0.03) starting from a maximally coherent array 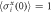 .
.
Download figure:
Standard image High-resolution imageLarge many-body correlations can lead to melting of the TC [8, 12]. For the purposes of quantifying the window of stability of the TC, we use the absolute value of the ratio between 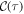 oscillation angular frequency, ω, and corresponding decay rate, B (or bandwidth) which is portrayed in figure 2(b). In our open system we can understand this behavior directly from the quantum regression theorem. While the lowest energy eigenstates of the Liouvillian with pure imaginary eigenvalue are the ones that determine the oscillatory character in the late-time synchronized state, excited eigenstates can contribute to the dynamics of the unequal time correlator through the term
oscillation angular frequency, ω, and corresponding decay rate, B (or bandwidth) which is portrayed in figure 2(b). In our open system we can understand this behavior directly from the quantum regression theorem. While the lowest energy eigenstates of the Liouvillian with pure imaginary eigenvalue are the ones that determine the oscillatory character in the late-time synchronized state, excited eigenstates can contribute to the dynamics of the unequal time correlator through the term 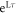 . For moderate interactions, low-lying Liouvillian eigenvectors will have eigenvalues with nonzero imaginary part and small, negative real part. These eigenvalues are dominant and determine the oscillation frequency. As interaction strength increases, however, so does the magnitude of the real part, which results in damping of the TC (see footnote 6). Such mechanism is also responsible for the growth of many-body correlations during the transient dynamics and thus directly manifest in the mutual information defined as IAB ≡ SA + SB − SAB, where
. For moderate interactions, low-lying Liouvillian eigenvectors will have eigenvalues with nonzero imaginary part and small, negative real part. These eigenvalues are dominant and determine the oscillation frequency. As interaction strength increases, however, so does the magnitude of the real part, which results in damping of the TC (see footnote 6). Such mechanism is also responsible for the growth of many-body correlations during the transient dynamics and thus directly manifest in the mutual information defined as IAB ≡ SA + SB − SAB, where ![${S}_{\alpha }=-\mathrm{Tr}[{\hat{\rho }}_{\alpha }\mathrm{log}[{\hat{\rho }}_{\alpha }]]$](https://content.cld.iop.org/journals/1367-2630/20/12/123003/revision2/njpaaf18bieqn48.gif) is the Von Neumann entropy computed from the reduced density matrix
is the Von Neumann entropy computed from the reduced density matrix 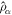 of the subsystem α = A, B, AB (AB is the joint subsystem).
of the subsystem α = A, B, AB (AB is the joint subsystem).
To establish a more formal connection between the TC stability and the growth of many-body correlations, we have computed the derivative of the mutual information for the case when A and B are single spin subsystems, starting from a maximally coherent initial state (all spins pointing along the 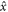 -direction). We find that in the large N limit and short characteristic times
-direction). We find that in the large N limit and short characteristic times 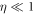 (respect to the oscillation period), with η ≡ f N Γτ, the growth rate of the mutual information approaches
(respect to the oscillation period), with η ≡ f N Γτ, the growth rate of the mutual information approaches 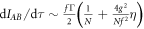 and thus remains irrelevant for
and thus remains irrelevant for 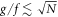 . This parameter regime is consistent with the range of g values where we observe that the TC forms. Outside this region, IAB grows rapidly with increasing g/f (see figure 2(c)). We explicitly indicate the contours g/f ∝ 1/N and
. This parameter regime is consistent with the range of g values where we observe that the TC forms. Outside this region, IAB grows rapidly with increasing g/f (see figure 2(c)). We explicitly indicate the contours g/f ∝ 1/N and 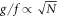 set by
set by 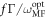 and the onset of fast mutual information growth, respectively, in figure 2(b). From these considerations we can conclude that the superradiant crystal only exists in the parameter regime where many-body correlations are subdominant and thus it can be regarded as an emergent semi-classical non-equilibrium state of matter.
and the onset of fast mutual information growth, respectively, in figure 2(b). From these considerations we can conclude that the superradiant crystal only exists in the parameter regime where many-body correlations are subdominant and thus it can be regarded as an emergent semi-classical non-equilibrium state of matter.
Robustness to disorder
We now investigate the impact of inhomogeneous dephasing, 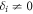 . For this, we resort to a second-order cumulant expansion [56], since in the absence of permutation symmetry exact numerical calculations are constrained to small systems, N ≲ 15. The complete set of equations of motion and equations for the two-time correlations are presented in the SM (see footnote 6). We find excellent agreement between the cumulant expansion and exact numerical solution of
. For this, we resort to a second-order cumulant expansion [56], since in the absence of permutation symmetry exact numerical calculations are constrained to small systems, N ≲ 15. The complete set of equations of motion and equations for the two-time correlations are presented in the SM (see footnote 6). We find excellent agreement between the cumulant expansion and exact numerical solution of 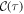 in the region where a stable TC is expected for the homogeneous (δi = 0) case, as well as for small system sizes in the presence of disorder (see footnote 6).
in the region where a stable TC is expected for the homogeneous (δi = 0) case, as well as for small system sizes in the presence of disorder (see footnote 6).
In figure 3(a) we show the robustness of the averaged equal time correlator 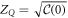 evaluated at optimal pumping Wopt to weak disorder Δ/(f Γ) within the relevant window of interactions g/f. One observes that finite elastic interactions protect the synchronized state against disorder, preserve phase coherence and favor spin alignment. While similar phase locking effects in the transient dynamics have been experimentally reported in cold atom experiments [38, 47–52], the interesting feature observed here is that the phase locking is achieved in the steady state of a driven dissipative system. Panels (b) and (c) of figure 3 portray the variation in oscillation frequency,
evaluated at optimal pumping Wopt to weak disorder Δ/(f Γ) within the relevant window of interactions g/f. One observes that finite elastic interactions protect the synchronized state against disorder, preserve phase coherence and favor spin alignment. While similar phase locking effects in the transient dynamics have been experimentally reported in cold atom experiments [38, 47–52], the interesting feature observed here is that the phase locking is achieved in the steady state of a driven dissipative system. Panels (b) and (c) of figure 3 portray the variation in oscillation frequency, ![$\delta \omega ({\rm{\Delta }})\equiv [\omega ({\rm{\Delta }})-\omega (0)]/\omega (0)$](https://content.cld.iop.org/journals/1367-2630/20/12/123003/revision2/njpaaf18bieqn59.gif) , and in the spectral width,
, and in the spectral width, ![$\delta B({\rm{\Delta }})\equiv [B({\rm{\Delta }})-B(0)]/B(0)$](https://content.cld.iop.org/journals/1367-2630/20/12/123003/revision2/njpaaf18bieqn60.gif) , of the averaged two-time correlation function determined from the cumulant expansion. The observed rigidity of the frequency also agrees with the simpler mean-field predictions (see footnote 6) which allow us to derive an analytic expression for the protection in the weak disorder limit:
, of the averaged two-time correlation function determined from the cumulant expansion. The observed rigidity of the frequency also agrees with the simpler mean-field predictions (see footnote 6) which allow us to derive an analytic expression for the protection in the weak disorder limit: 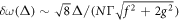 , where we observe the 1/N suppression gained from the collective nature of the elastic and dissipative interactions.
, where we observe the 1/N suppression gained from the collective nature of the elastic and dissipative interactions.
Figure 3. Finite interactions protect the TC against weak disorder as can be seen in: (a) the robustness of the averaged 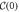 , the insensitivity of the time crystal's (b) frequency, δω(Δ), and (c) spectral width, δ B(Δ), to weak disorder Δ/(f Γ) for the relevant window of interactions g/f. All plots are computed using the second-order cumulant expansion at optimal pumping Wopt for N = 100 spins.
, the insensitivity of the time crystal's (b) frequency, δω(Δ), and (c) spectral width, δ B(Δ), to weak disorder Δ/(f Γ) for the relevant window of interactions g/f. All plots are computed using the second-order cumulant expansion at optimal pumping Wopt for N = 100 spins.
Download figure:
Standard image High-resolution imageExperimental realization and outlook
The superradiant crystal can be directly realized using an array of incoherently pumped atomic dipoles tightly trapped by a deep optical lattice that is supported by an optical cavity. The cavity couples two relevant internal states of the atoms, and operates in the bad cavity limit where the bare atomic linewidth γ is significantly smaller than the cavity linewidth κ. In this regime the cavity photons do not participate actively in the dynamics but instead mediate collective dissipative decay (superradiant emission) [35, 36, 57], with 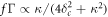 , and elastic exchange interactions, with
, and elastic exchange interactions, with 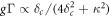 , which can be independently controlled by varying the cavity detunning δc from the atomic transition. The signature of the TC can then be directly observed in the spectrum of the light leaked from the cavity [38]. A similar implementation can be realized by replacing the cavity photons by phonons in an ion crystal [42]. In the case of the cavity, the order of magnitude for f Γ/2π and gΓ/2π is approximately 10−4 Hz. For typical atom number in the cavity, N ≈ 105, the TC oscillation frequency approaches ≈10 Hz. In the case of the ion crystal, we have f Γ/2π = gΓ/2π ≈ 6 Hz. In this case the TC oscillation frequency for typical ion number N ≈ 102 approaches ≈103 Hz.
, which can be independently controlled by varying the cavity detunning δc from the atomic transition. The signature of the TC can then be directly observed in the spectrum of the light leaked from the cavity [38]. A similar implementation can be realized by replacing the cavity photons by phonons in an ion crystal [42]. In the case of the cavity, the order of magnitude for f Γ/2π and gΓ/2π is approximately 10−4 Hz. For typical atom number in the cavity, N ≈ 105, the TC oscillation frequency approaches ≈10 Hz. In the case of the ion crystal, we have f Γ/2π = gΓ/2π ≈ 6 Hz. In this case the TC oscillation frequency for typical ion number N ≈ 102 approaches ≈103 Hz.
Having demonstrated the rigidity of the TC to dephasing, now we discuss its rigidity to variations in the system's parameters. For the proposed cavity implementation,  . From this expression, one can see
. From this expression, one can see 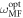 is not highly sensitive to variations in the cavity linewidth, κ, but on the contrary it is linearly sensitive to variations on δc and N. Systematics in the cavity detuning, nevertheless, can be currently controlled at the subhertz level by locking the cavity to a state-of-the-art clock laser [58]. Fluctuations in N can be also suppressed by operating the system in a three dimensional optical lattice in the band or Mott insulator regimes [59] and spectroscopically selecting a fixed region of the atomic array [60].
is not highly sensitive to variations in the cavity linewidth, κ, but on the contrary it is linearly sensitive to variations on δc and N. Systematics in the cavity detuning, nevertheless, can be currently controlled at the subhertz level by locking the cavity to a state-of-the-art clock laser [58]. Fluctuations in N can be also suppressed by operating the system in a three dimensional optical lattice in the band or Mott insulator regimes [59] and spectroscopically selecting a fixed region of the atomic array [60].
In summary, we have proposed and investigated the emergence of a TC in a many-body driven dissipative quantum system. By investigating its stability to quantum correlations we showed that it only exists in the parameter regime where many-body correlations are subdominant and thus can be regarded as an emergent semi-classical non-equilibrium state of matter. However, it is important to emphasize that this system is fundamentally distinct from the prototypical laser. This can be seen from the fact that the working mechanism of a laser is stimulated emission, an ingredient absent in our setup. Lasing action is possible even in a single atom system or in the absence of coupling between the atomic dipoles. The superradiant TC, on the contrary, is a genuine many-body phenomenon that happens in the bad cavity limit where the mean photon number in the cavity is less than one. However, even without stimulated emission, superradiance can happen due to collective interactions in a many-body array of long lived atomic dipoles. The superradiant TC is thus a genuine many-body phenomenon which can produce spectrally pure light and might find direct applications in 'interaction-enhanced quantum' sensing.
Acknowledgments
We acknowledge useful discussions with I Bloch, M Foss-Feig, M Holland, A. Shankar, J Thompson and P Zoller. The authors acknowledge support from Defense Advanced Research Projects Agency (DARPA) and Army Research Office grant W911NF-16-1-0576, NSF grant PHY1820885, JILA-NSF grant PFC-173400, and the Air Force Office of Scientific Research FA9550-18-1-0319 and its Multidisciplinary University Research Initiative grant FA9550-13-1-0086, and NIST. JM is supported by the European Union's Framework Programme for Research and Innovation Horizon 2020 2014–2020 under the Marie Sklodowska-Curie Grant Agreement No. 745608 ('QUAKE4PRELIMAT'). B Zhu was supported by the NSF through a grant for the Institute for Theoretical Atomic, Molecular, and Optical Physics at Harvard University and the Smithsonian Astrophysical Observatory.
Footnotes
- 7
see supplementary material available online at stacks.iop.org/NJP/20/123003/mmedia.