Abstract
We analyze the Newton flow of the Riemann zeta function ζ and rederive in an elementary way the Riemann–von Mangoldt estimate of the number of non-trivial zeros below a given imaginary part. The representation of the flow on the Riemann sphere highlights the importance of the North pole as the starting and turning point of the separatrices, that is of the continental divides of the Newton flow. We argue that the resulting patterns may lead to deeper insight into the Riemann hypothesis. For this purpose we also compare and contrast the Newton flow of ζ with that of a function which in many ways is similar to ζ, but violates the Riemann hypothesis.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
'One now finds indeed approximately this number of real roots within these limits, and it is very probable that all roots are real'6 . The phrase 'this number' from the quote of Bernhard Riemann's seminal article [1] of 1859 on the distribution of primes refers to the estimate
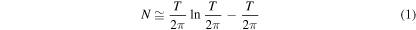
for the number N of non-trivial zeros of the Riemann zeta function ζ with an imaginary part between zero and T. Moreover, the claim that 'all roots are real' constitutes the famous Riemann hypothesis [2, 3] that all non-trivial zeros lie on the critical line with real part  In the present article we suggest a new approach towards the Riemann hypothesis based on a concept from physics, that is the flow of a dynamical system.
In the present article we suggest a new approach towards the Riemann hypothesis based on a concept from physics, that is the flow of a dynamical system.
In a recent article [4] we have illustrated the Newton flow [5] of a complex-valued function using several examples including ζ. The present article is different in three respects: (i) we demonstrate the power of the Newton flow by presenting an elementary derivation of the estimate equation (1), (ii) we focus on the flow on the Riemann sphere rather than the complex plane, and (iii) we employ the topology of the flow to obtain a different point of view on the Riemann hypothesis. Indeed, we show that this representation is perfectly suited to address the Riemann hypothesis since the North pole is the accumulation point of the zeros and the critical line becomes a tangent of the 90° meridian.
1.1. Flows of ζ
The flow lines of the continuous Newton method [5] for a given function are lines where the phase of this function is constant. Curves where ζ assumes real values are a special class of these flow lines and have been studied in great detail in the Doktorarbeit by Albert Arnold Utzinger [6] in 1934, and more recently by Hugh Lowell Montgomery and John Griggs Thompson [7]. They are at the very heart of an equivalent formulation of the Riemann hypothesis put forward by Andreas Speiser [8]: all non-trivial zeros of the first derivative are to the right of the critical line.
Curves in the complex plane where ζ is purely real or purely imaginary have been analyzed over a large range of arguments of ζ in [9]. Since the emerging picture resembles the x-ray photograph of the skeleton of a body this work carries the suggestive title 'X-ray of Riemann zeta function'. In our article we go further and find all flow lines of ζ.
We emphasize that our approach is also different from [10] which discusses the holomorphic rather than the Newton flow of ζ. Indeed, the continuous Newton method distinguishes [5] between the zeros of the function which are sinks and the poles which are sources of the flow. In contrast, in the holomorphic flow the zeros can be sinks or sources.
It is also worth mentioning that [11] introduces a family of parametrized zeta functions and studies the flow of the corresponding zeros on the Riemann sphere as the functions tend towards ζ. In this parameter flow the zeros approach the equator. In contrast, we focus exclusively on the Riemann zeta function and the generated Newton flow is associated with every point of the complex plane. In the present article the zeros are stationary and the flow lines terminate in them.
1.2. ζ in physics
The important role of the Riemann zeta function in number theory [12] and, in particular, in the distribution of primes is well known. For this reason ζ has been the topic of extensive research [13–15] exemplified by the celebrated asymptotic formulae of Carl-Ludwig Siegel [16], and Michael Victor Berry and John Peter Keating [17]. They suggest that the Riemann hypothesis is indeed correct. The strongest support of this assertion is the work of Xavier Gourdon and Patrick Demichel [18] who have numerically verified that the first 1013 zeros of ζ are on the critical line.
We emphasize that ζ appears not only at the interface of number theory and quantum physics such as the factorization of numbers with Bose–Einstein condensates [19] but is prevalent in physics [10, 20]. To illustrate this point we list only a few physical phenomena where ζ manifests itself.
For example,  is hidden in the constant of the Stefan–Boltzmann law [21] of black-body radiation connecting the energy density and the fourth power of the temperature. Indeed, the numerical factor emerging from the integration of the Planck law over frequency contains this value.
is hidden in the constant of the Stefan–Boltzmann law [21] of black-body radiation connecting the energy density and the fourth power of the temperature. Indeed, the numerical factor emerging from the integration of the Planck law over frequency contains this value.
We emphasize that there also exist interesting connections between the distribution of non-trivial zeros of ζ and random matrix theory [22, 23], or the eigenvalue distribution of Hermitian matrices [24, 25]. Moreover, the entanglement [26] of quantum systems [27, 28] is a necessary resource to construct [29] a quantum simulator for ζ. We also note the appearance of ζ in the partition function of a Bose–Einstein condensate [30–32], and in radiation patterns [33] as first observed by Balthasar van der Pol [34]. This way of creating ζ is also closely related to the quantum Mellin transform [35].
1.3. Outline
Our article is organized as follows: in section 2 we briefly summarize the essential ingredients of the continuous Newton method and apply it in section 3 to the Riemann zeta function in the complex plane. Here we employ the flow lines corresponding to phases which are integer multiples of π to rederive the Riemann–von Mangoldt formula, equation (1). Section 4 contains our discussion of the Newton flow of ζ on the Riemann sphere. We conclude in section 5 by summarizing our results, indicating a different approach towards the Riemann hypothesis and analyzing the Newton flow of a function which resembles ζ but does not satisfy the Riemann conjecture.
In the appendix we compare and contrast the Newton flows of ζ and the sine function. In particular, we use the asymptotic properties of the flow lines to show that the zeros of sine are on the real axis. This comparison serves us as our motivation that indeed the Newton flow of ζ can provide insight into the Riemann hypothesis.
2. Continuous Newton method
In the present section we lay the ground work for our analysis of the Newton flow of the Riemann zeta function. For this purpose we briefly review the main features of the continuous Newton method. Here, we motivate several properties and refer for the detailed proofs to the literature [4, 5, 36].
The solutions 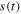 of the differential equation
of the differential equation
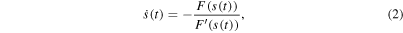
form the flow lines of the complex function F(s) where F' denotes the Fréchet derivative. They are given implicitly by the relation
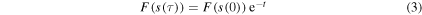
which shows that along the line going through the point s(0) the phase is constant and determined by the initial condition 
Moreover, the Newton flow for 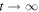 approaches a zero of F independently from s(0). This fact might be expected since the differential equation, equation (2), defining the Newton flow is the continuous version of the discrete Newton method to find zeros of a function.
approaches a zero of F independently from s(0). This fact might be expected since the differential equation, equation (2), defining the Newton flow is the continuous version of the discrete Newton method to find zeros of a function.
Hence, zeros of F act like sinks for the Newton flow. In this way, the continuous Newton method is reminiscent of a steepest descent method [37]. Indeed, it is one with respect to an appropriately chosen gradient, the so-called Sobolev gradient [38].
The inner workings of the continuous Newton method stand out most clearly for the following two elementary examples: (i) A simple zero given by  leads via equation (3) to
leads via equation (3) to
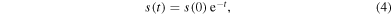
which shows that for  the flow approaches the zero at the origin of the complex plane.
the flow approaches the zero at the origin of the complex plane.
(ii) In contrast, for a simple pole, that is 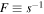 we find from equation (3) the trajectories
we find from equation (3) the trajectories
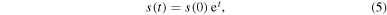
and compared to the example of a simple zero, the time is inverted. Hence, poles are sources of the Newton flow.
These two examples also show that infinity can be both, a sink and a source. In the case of the simple zero infinity is the source, whereas for the simple pole infinity serves as a sink.
Of special interest are flow lines which go through a point where the derivative F' vanishes. Since F' is in the denominator of the definition, equation (2), of the Newton flow, in such points, referred to as hyperbolic points [5], the forward uniqueness of the trajectories gets lost.
For a simple zero of F' located at  two flow lines cross. The two outgoing parts of the lines end at two different zeros and are orthogonal to the incoming parts. Since the phase of a flow line is determined by the value of F at every point of the line the phases along the two lines are identical and given by
two flow lines cross. The two outgoing parts of the lines end at two different zeros and are orthogonal to the incoming parts. Since the phase of a flow line is determined by the value of F at every point of the line the phases along the two lines are identical and given by 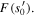
Only in a hyperbolic point can the lines of the Newton flow cross each other and separate in this way different domains of sinks and sources of the flow. We call these continental divides separatrices. At a point  where the mth derivative of F does not vanish but all lower ones do there are m separatrices crossing each other [5].
where the mth derivative of F does not vanish but all lower ones do there are m separatrices crossing each other [5].
We emphasize that these considerations about separatrices are confined to functions given by polynomials. However, the situation gets more complicated when we are faced with functions that cannot be represented as a polynomial of finite degree. In the next section we will show that there exist infinitely many hyperbolic points of ζ in infinity and the Newton flow on the Riemann sphere discussed in section 4 reveals that at the North pole of the sphere infinitely many separatrices cross.
3. Newton flow of ζ in the complex plane
We now illustrate the continuous Newton method outlined in the preceding section by applying it to the Riemann zeta function. For this purpose we recall that for real parts  of the complex argument
of the complex argument 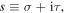 ζ is defined by the Dirichlet series
ζ is defined by the Dirichlet series
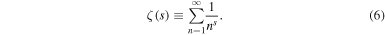
For arguments s to the left of the line s = 1 there exists [2] an analytical continuation of ζ based on the functional relation
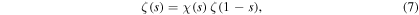
where
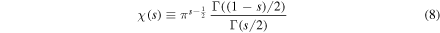
contains the gamma function Γ.
We first find the separatrices of ζ in the complex plane and, in particular, identify hyperbolic points for  We then perform an asymptotic analysis of ζ to locate the lines where ζ is real as
We then perform an asymptotic analysis of ζ to locate the lines where ζ is real as  and
and 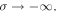 This calculation allows us to connect the Riemann–von Mangoldt formula, equation (1), to the flow lines with phase π.
This calculation allows us to connect the Riemann–von Mangoldt formula, equation (1), to the flow lines with phase π.
3.1. Classification of separatrices
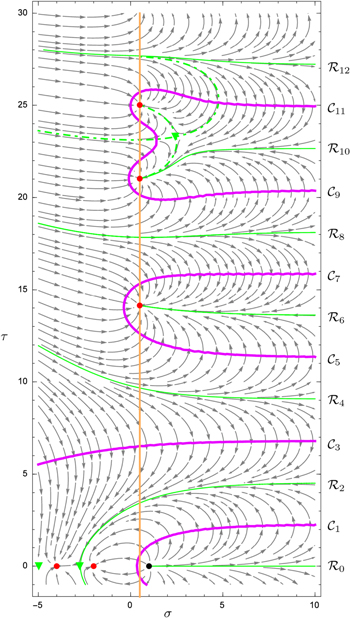
Figure 1 represents the Newton flow of ζ defined by equations (6)–(8) in the complex plane, and discussed in more detail in [4]. We recognize the role of the pole at s = 1, indicated by a black dot, as a source and the first trivial zero at s = −2, depicted by a red dot, as a sink. Moreover, the flow converges towards the trivial zeros at s = −2k, with 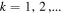 on the real axis, or the non-trivial zeros along the critical axis
on the real axis, or the non-trivial zeros along the critical axis  represented by an orange line.
represented by an orange line.
Figure 1. Newton flow of the Riemann zeta function in the complex plane given by the argument  in the neighborhood of the critical line
in the neighborhood of the critical line 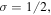 indicated by the orange line. The pole and the zeros are represented by a black and red dots, respectively. The locations of the zeros of ζ', that is of the first derivative of ζ are marked by green triangles, and the green curves define the separatrices. The picture appears to be symmetric with respect to the real axis, however, for
indicated by the orange line. The pole and the zeros are represented by a black and red dots, respectively. The locations of the zeros of ζ', that is of the first derivative of ζ are marked by green triangles, and the green curves define the separatrices. The picture appears to be symmetric with respect to the real axis, however, for  the phase of ζ on the flow lines is opposite to the one on the lines for
the phase of ζ on the flow lines is opposite to the one on the lines for 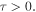
Download figure:
Standard image High-resolution imageHowever, the main players of figure 1 are the separatrices which direct the flow into the individual basins of attractions, that is the zeros of ζ. We identify three classes of separatrices: (i) the first one contains those that go through a trivial zero of ζ', that is a hyperbolic point on the negative real axis, and terminate at a trivial zero of ζ with 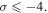 (ii) The second class consists of those that run from the left to the right of figure 1 and then return from there to terminate at a non-trivial zero. We will see that the separatrix emerging from the pole at s = 1 and continuing through the first trivial zero of ζ' at
(ii) The second class consists of those that run from the left to the right of figure 1 and then return from there to terminate at a non-trivial zero. We will see that the separatrix emerging from the pole at s = 1 and continuing through the first trivial zero of ζ' at  to the two trivial zeros of ζ at −2 and −4 is a mixture of both classes. (iii) The third class is defined by the separatrices that start on the left and go through a non-trivial zero of ζ' to conclude in a non-trivial zero of ζ.
to the two trivial zeros of ζ at −2 and −4 is a mixture of both classes. (iii) The third class is defined by the separatrices that start on the left and go through a non-trivial zero of ζ' to conclude in a non-trivial zero of ζ.
3.2. Hyperbolic points at 
Since all separatrices are connected to hyperbolic points we suspect from the separatrices of type (ii) that ζ' vanishes for 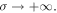 Indeed, the two lowest terms
Indeed, the two lowest terms
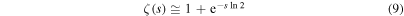
of the Dirichlet series, equation (6), yield

which vanishes in the limit of  at the imaginary parts
at the imaginary parts
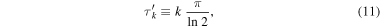
with 
Moreover, from the asymptotic expansion, equation (9), we find
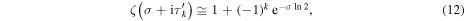
and as σ approaches infinity, ζ tends to unity. Hence, at the hyperbolic points at infinity ζ is real and identical to unity.
Since the flow lines are lines of constant phase, ζ is real and positive along these separatrices. In particular, the part of the separatrix which is associated with the imaginary part  is the real axis to the right of the pole at s = 1.
is the real axis to the right of the pole at s = 1.
The consecutive curves corresponding to even values of k are the parts of the separatrices of class (ii) which run from the left to the right of figure 1. Along all of these lines ζ is larger than unity.
However, for odd values of k the separatrices 'start' at  and approach a non-trivial zero of ζ. Along these lines the value of ζ decays from unity to zero.
and approach a non-trivial zero of ζ. Along these lines the value of ζ decays from unity to zero.
Moreover, we find that  is special. Indeed, the lines emerging from
is special. Indeed, the lines emerging from 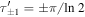 meet each other in the first trivial zero of ζ' at
meet each other in the first trivial zero of ζ' at 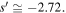
Therefore, all flow lines starting at the pole s = 1 are directed to the first trivial zero of ζ at s = −2, whereas the source of all other flow lines is 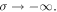
In order to bring out these features of the Newton flow most clearly we display in figure 2 the Riemann zeta function in a rather unusual way in the complex plane. Indeed, we show the function
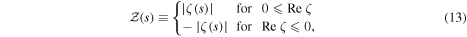
that is we depict 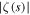 for all arguments s where
for all arguments s where 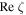 is positive, but plot
is positive, but plot 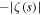 for all s where
for all s where 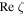 is negative.
is negative.
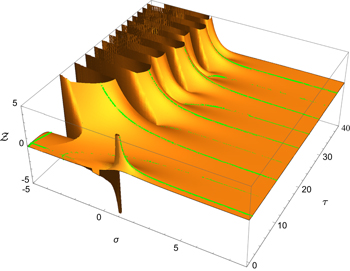
Figure 2. Lines in the complex plane where the Riemann zeta function ζ is real (green) depicted on a relief representing the positive absolute value of ζ for arguments  where the real part of ζ is positive, and the negative absolute value of ζ where the real part of ζ is negative. This representation brings out most clearly that the lines of constant phase corresponding to phases of integer multiples of
where the real part of ζ is positive, and the negative absolute value of ζ where the real part of ζ is negative. This representation brings out most clearly that the lines of constant phase corresponding to phases of integer multiples of 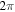 run down the hills on the left-hand side, turn around on the right and terminate in the non-trivial zeros. This pattern repeats itself infinitely many times. The points of arrival and departure on the right-hand side of the picture are equally spaced and given by equation (11).
run down the hills on the left-hand side, turn around on the right and terminate in the non-trivial zeros. This pattern repeats itself infinitely many times. The points of arrival and departure on the right-hand side of the picture are equally spaced and given by equation (11).
Download figure:
Standard image High-resolution imageAlong the green flow lines ζ is real. In the foreground of figure 2 they run most of the time in the plane. An exception is the line along the real axis which descends from the pole at s = 1.
However, for larger values of τ the green lines undergo an infinite change in altitude. They come from the left where ζ is positive infinite, run down the hills to the plains and turn around at values of s where σ is positive infinite. They then continue their descent till they reach a non-trivial zero.
The green lines of figure 2 which represent separatrices play also a prominent role in the analysis of [7] where they are called  and defined for even k as the 'connected component on which
and defined for even k as the 'connected component on which 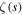 is positive real with asymptote
is positive real with asymptote  as
as  ' This asymptote corresponds to
' This asymptote corresponds to 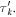
In addition, the lines of constant height 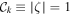 are crucial. Indeed, according to [7] they are defined for odd k as 'the connected component on which
are crucial. Indeed, according to [7] they are defined for odd k as 'the connected component on which  with asymptote
with asymptote 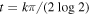 as
as  '. Hence, these lines run in between two consecutive separatrices that cross the complex plane. Since the Newton flow consists of lines of constant phase the flow lines are orthogonal to the lines of
'. Hence, these lines run in between two consecutive separatrices that cross the complex plane. Since the Newton flow consists of lines of constant phase the flow lines are orthogonal to the lines of 
In order to connect our work with that of [7] we show in figure 3 the Newton flow in the neighborhood of the first three non-trivial zeros together with the curves 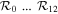 and
and 
Figure 3. Newton flow in the complex plane together with the lines of constant height  (violet curves) and lines
(violet curves) and lines 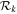 (green solid curves) where ζ is real analyzed in [7].
(green solid curves) where ζ is real analyzed in [7].
Download figure:
Standard image High-resolution image3.3. Number of non-trivial zeros below a given number
All flow lines end in a zero of the function. Hence, at the non-trivial zeros of ζ a trajectory with the phase given by an integer multiple of π terminates which is the continuation of the separatrix coming from the right. We now address the question if we can identify this line in the representation of ζ for 
From the analytic continuation, equation (7), of ζ we find
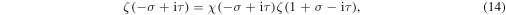
that is
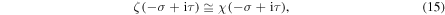
where in the last step we have used the asymptotic value 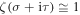 following from equation (9) for
following from equation (9) for 
With the help of the asymptotic expansion [2]
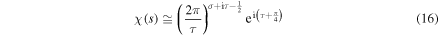
valid in any fixed strip 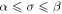 for
for  we find from equation (15) the expression
we find from equation (15) the expression

Hence, for a fixed but large negative value of σ the condition

for an integer j yields values of  where ζ is real. However, at this point we have to recall that the expansion equation (16) is only valid for
where ζ is real. However, at this point we have to recall that the expansion equation (16) is only valid for  Hence, the condition equation (18) only holds true starting from appropriately large values of j.
Hence, the condition equation (18) only holds true starting from appropriately large values of j.
Some of the even values of j correspond to the separatrices running from the left to the right side of figure 1 and some of them end in a non-trivial zero.
However, all odd values of j lead directly to a non-trivial zero. As a result, we can count the non-trivial zeros when we cast equation (18) for  into the form
into the form
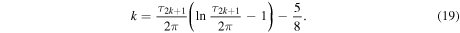
Hence, the number N of non-trivial zeros with imaginary parts smaller than T is given by 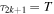 which yields
which yields
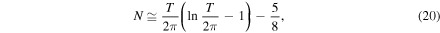
in complete agreement with the Riemann–von Mangoldt formula, equation (1).
We conclude this section by noting that the Newton flow of ζ provides us not only with some qualitative insight into the function, but also has a predictive power. Indeed, it allow us to rederive the asymptotic expression, equation (1), of the number of zeros. A similar calculation based on the lines where ζ is real can also be found in [9].
4. Newton flow of ζ on the Riemann sphere
The analysis of the preceding section shows that the behavior of the separatrices at infinity rules the flow patterns in the neighborhood of the critical line. In order to obtain a different perspective on ζ at infinity we dedicate the present section to a discussion of the Newton flow of ζ using the Riemann sphere. The latter is a unit sphere whose South pole is at the origin of the σ–τ-plane. The intersection
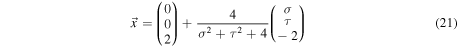
of the straight line connecting the point 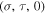 and the North pole
and the North pole  of the sphere defines the transformation of the points of the complex plane onto the surface of the sphere. Throughout this section, we make contact with the flow in the complex plane exemplified by figure 1.
of the sphere defines the transformation of the points of the complex plane onto the surface of the sphere. Throughout this section, we make contact with the flow in the complex plane exemplified by figure 1.
4.1. Pole and trivial zeros
In figure 4 we show the Newton flow of ζ on the Riemann sphere in the domain governed by the pole and the first trivial zero of ζ. In order to focus on the essential parts, we have omitted close to the North pole most of the field lines creating a bold top.
Figure 4. Newton flow of ζ on the Riemann sphere in the neighborhood of the pole of ζ indicated by the black dot (right picture), and of the first trivial zero, marked by the red dot closest to the South pole (left picture). The red arrows cut through the South and the North poles and the two spheres are rotated around this axis by slightly less than 180°. The Southern hemisphere is dominated by the flow lines emerging from the pole and converging to the first trivial zero. Close to the line connecting the pole of ζ with the North pole, corresponding to the positive real axis of the complex plane and displayed in violet, the Newton flow makes an excursion deep into the Northern hemisphere as indicated by the sphere on the right. However, in the neighborhood of the first trivial zero the flow is confined exclusively to the Southern hemisphere by the separatrix through the first trivial zero of ζ' given by the green line and the Southernmost green triangle, respectively. The red dots and green triangles above indicate the trivial zeros of ζ and ζ' on the real negative axis marked in violet, respectively.
Download figure:
Standard image High-resolution imageThe point 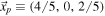 corresponding to the pole of ζ at s = 1, marked in the right picture by a black dot, is the source of all flow lines which terminate in the first trivial zero s = −2, represented by a red dot in the left picture. Here, we have also indicated by red dots the other trivial zeros.
corresponding to the pole of ζ at s = 1, marked in the right picture by a black dot, is the source of all flow lines which terminate in the first trivial zero s = −2, represented by a red dot in the left picture. Here, we have also indicated by red dots the other trivial zeros.
The pole and the trivial zeros lie on a great circle, indicated in the pictures by the violet line. This circle is the result of the mapping equation (21) of the real axis of the complex plane onto the Riemann sphere. In analogy to the globe we call the image of the positive real axis with the pole of ζ on it the zero-degree, or the Greenwich meridian.
The opposite meridian, which is the image of the negative real axis, contains all the trivial zeros as also apparent from figure 5. Here, we present a view from the top almost along the vertical axis through the North pole. This figure also brings out the fact that the symmetry of the flow with respect to the real axis, mentioned in connection with figure 1, translates into a symmetry with respect to this great circle.
Figure 5. Newton flow of ζ on the Northern hemisphere of the Riemann sphere where the North pole serves as a source. The green line in the form of a cardioid emerging from the pole to the right and running mostly on the edge of the globe is the separatrix already shown in figure 4. The first trivial zero is the red dot to the left of this separatrix on the left side of the sphere. The other trivial zeros are on the violet line converging towards the North pole. The non-trivial zeros are located symmetrically with respect to this line and move towards the North pole on the critical axis indicated by the orange line. They are separated from the trivial zeros by the second green line representing another separatrix and are therefore confined to a rather small region near the North pole. To bring out this structure more clearly we magnify this area in figure 6.
Download figure:
Standard image High-resolution imageThe two separatrices circumventing in figure 1 the pole from the right and approaching the first two trivial zeros through the first trivial zero of ζ', depicted there by the green solid lines start on the sphere from the North pole, almost approach the equator in the first trivial zero of ζ' as shown on the left picture of figure 4 and then annihilate in the first two trivial zeros.
This line is the green cardioid-like curve of figure 5 confining the flow to the North pole. Indeed, this trajectory separates the flow lines emerging from the pole of ζ and dominating the behavior in the Southern hemisphere from those coming out of the North pole of the globe governing the Northern hemisphere.
4.2. The non-trivial zeros close to the North pole
The trefoil structure shown in figure 5 which is reminiscent of the club card, rotated here by 90°, is a consequence of the interplay between the trivial zeros along the 180° meridian and the non-trivial zeros located along a path (orange line) orthogonal to it. According to figure 1 they are separated from each other by a separatrix which runs from minus infinity to plus infinity. This separatrix translates into the next inner green curve located close to the North pole and defines the transverse structure of the club. Its top and the bottom parts are given by the approach of the trivial zeros and the excursion of the flow lines from the pole of ζ on the Southern hemisphere towards the North pole, respectively.
Since both types of zeros tend towards infinity the behavior on the North pole gets rather crowded. In figure 6 we magnify the Newton flow on the Riemann sphere along the positive critical line.
Figure 6. Newton flow of ζ close to the North pole of the Riemann sphere along the positive critical line. On the green and blue lines ζ assumes real values. Along the outer separatrix emerging from the North pole to the left ζ descends from plus infinity to unity as it circumvents the first non-trivial zero reaching the North pole from the right. The descent of ζ continues on the next inner separatrix leaving the North pole to the right and terminating at the first non-trivial zero. As we backtrack the blue line towards the North pole ζ assumes ever increasing negative values. This left–right–left oscillation repeats itself infinitely many times along the next separatrices with one modification: between two consecutive real positive-valued separatrices emerging from the left and propagating to the right of the North pole there exist several non-trivial zeros. However, the separatrix leaving the North pole to the right can only end in one of these non-trivial zeros. Hence, the separatrices dividing the flow lines between the zeros of the same group and starting towards the left of the North pole have to traverse a hyperbolic point close to the right of the critical line where ζ' vanishes. Here they undergo a bifurcation and conclude in the two neighboring non-trivial zeros. Although we indicate here only the case of the second and third non-trivial zero (light blue line) we emphasize that this behavior is prevalent as the non-trivial zeros of ζ and ζ' approach the North pole.
Download figure:
Standard image High-resolution imageFrom section 2 we recall that for a hyperbolic point corresponding to a simple zero of F' we have the crossing of two separatrices. To the right of the critical line there are infinitely many separatrices that enter the North pole reflecting the fact that we have infinitely many hyperbolic points at infinity characterized by the imaginary parts 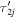 defined by equation (11).
defined by equation (11).
However, there are also infinitely many separatrices that leave the North pole. They result from the points in infinity with the imaginary parts  The deeper reason for the crossing of infinitely many separatrices at the North pole is the fact that here we do not deal with a polynomial but an exponential function presented in equation (10).
The deeper reason for the crossing of infinitely many separatrices at the North pole is the fact that here we do not deal with a polynomial but an exponential function presented in equation (10).
A separatrix approaching the North pole is always followed by an emerging one and we can interpret the two as one and the same trajectory especially since the value of ζ at the North pole along all of these separatrices is unity. However, this trajectory has a kink at the North pole corresponding to the different imaginary parts  and
and 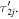
In contrast, the separatrices on the left of the critical line all start from the North pole. On the ones where ζ is positive ζ tends towards plus infinity as we reverse the path and approach the North pole. These separatrices are the ones which enter the North pole from the right. They then leave the North pole to the right and are met in the non-trivial zero by flow lines leaving the North pole to the left. On one of them (blue line) ζ is negative and tends to minus infinity as we backtrack the flow line towards the North pole.
This behavior is interrupted at the second non-trivial zero of ζ. Here a hyperbolic point appears slightly to the right of the critical line as shown in figure 6 and two separatrices that both emerge to the left of the North pole cross each other. Along these lines ζ is not real but given by the phase of ζ at the hyperbolic point. This phenomenon repeats itself infinitely many times as we consider non-trivial zeros with ever increasing imaginary parts.
So far we have concentrated on the very special class of flow lines emerging from the left of the North pole where ζ is real and the phase is either zero or π. However, there are infinitely many flow lines covering continuously all phases from zero to  Hence, along these lines ζ assumes all values as we backtrack them towards the North pole. Since there are infinitely many zeros this continuous change of the phase repeats itself infinitely many times. The resulting rapid oscillations close to the North pole are in complete accordance with the theorem of Picard [39] and reflect the fact that the North pole is an essential singularity.
Hence, along these lines ζ assumes all values as we backtrack them towards the North pole. Since there are infinitely many zeros this continuous change of the phase repeats itself infinitely many times. The resulting rapid oscillations close to the North pole are in complete accordance with the theorem of Picard [39] and reflect the fact that the North pole is an essential singularity.
4.3. The compression of the edge of infinity
As the critical line approaches the North pole it becomes a tangent to the 90° meridian. Moreover, the non-trivial zeros and the associated separatrices and lines where ζ is negative accumulate at the North pole. As the imaginary parts of the non-trivial zeros increase these lines now cover an ever smaller domain of the polar cap. This localization is a consequence of the stereographic projection defined by equation (21).
There is one more feature that adds to the complexity of the flow close to the North pole. As the imaginary part τ grows, that is as we approach the polar cap, the number of zeros caught between two separatrices running from the left to the right increases. This property is not apparent from figures 1 and 4 but is clearly visible in figure 10 of [4]. As a result, more and more zeros get cramped in less and less space and it seems that the complexity of the Newton flow gets intractable.
We are therefore wondering if the use of the Riemann sphere rather than the familiar complex plane can offer an advantage in the discussion of the Riemann hypothesis.
Indeed, in the Newton flow of ζ in the complex plane displayed in figure 1 these lines range in their real parts from minus infinity to plus infinity and the asymptotic formulae equations (9) and (17) are only valid at infinity and not in the critical strip. However, after the stereographic projection of ζ we might be able to find elementary expressions for the Newton flow lines close to the North pole which are valid along the complete line. Such an approach might even help to unravel the accumulation of the zeros predicted by the Riemann–von Mangoldt formula, equation (1). Unfortunately this problem goes beyond the scope of the present paper.
5. Summary
In the present article we have analyzed the Riemann zeta function with the help of the continuous Newton method which brings out the lines of constant phase of ζ. They emerge either from the pole of ζ, or from infinity, and converge towards the zeros of ζ without ever crossing each other. Since there is an infinite number of them there are infinitely many separatrices which define the different basins of attractions given by the zeros. These separatrices are the only flow lines that can cross each other and the crossing takes place in the zeros of ζ'.
Due to the importance of the behavior of ζ in infinity we have studied the Newton flow on the Riemann sphere. In this representation the main action takes place in the neighborhood of the North pole and the separatrices form onion-shaped layers with ever decreasing surface area. Indeed, it is the topology of these lines which we hope will open a new approach towards the Riemann hypothesis.
In a proof based on contradiction we first negate the Riemann hypothesis and obtain from the claim that all non-trivial zeros are on the critical axis the assumption that at least one non-trivial zero would not lie there. As a consequence of the functional equation (7) of ζ the existence of a non-trivial zero off the critical axis implies an additional zero which is symmetrically located with respect to the critical axis.
At this point we recall that the function [3]
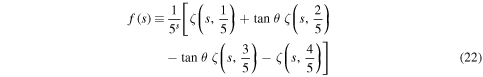
defined as a linear combination of Hurwitz zeta functions
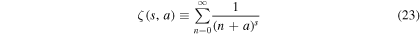
of different parameters a with
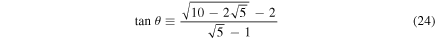
is very similar to the Riemann zeta function. In particular, it satisfies the functional equation
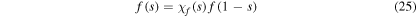
with
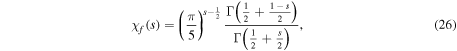
which is reminiscent of the corresponding equation equation (7) for ζ.
Nevertheless, f does not obey the Riemann hypothesis. Although most of the non-trivial zeros of f lie on the critical line there are exceptions. Indeed, in figure 7 we show the Newton flow around the imaginary part 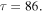 Here we find two zeros which are located symmetrically around the critical axis as required by the functional equation, equation (25). Nevertheless, the flow adjusts itself and a separatrix separates the two zeros.
Here we find two zeros which are located symmetrically around the critical axis as required by the functional equation, equation (25). Nevertheless, the flow adjusts itself and a separatrix separates the two zeros.
Figure 7. Newton flow of the function f defined by equation (22), which is known [3] not to satisfy the Riemann hypothesis but is otherwise very close to ζ. Although most of its non-trivial zeros are along the critical line (orange) there are exceptions as shown by the pair of zeros with identical imaginary parts at the center of the picture. Despite this deviation from the rule the Newton flow adjusts to the presence of the pair. We emphasize that the hyperbolic point (green triangle) is to the left of the critical line in complete agreement with the Speiser formulation of the Riemann hypothesis.
Download figure:
Standard image High-resolution imageThe example of f may well be an indication that a proof of the Riemann hypothesis along the lines of the Newton flow requires an additional property of the Riemann zeta function that we have not used in our argument so far. Indeed, the example of the sine function discussed in the appendix whose Newton flow enjoys several similarities with that of ζ requires the well-known trigonometric relation  in the proof that all zeros of sine are on the real axis. Hence, we suspect that a similar formula is needed to prove or disprove the Riemann hypothesis. However, it is not clear what this relation for ζ would be.
in the proof that all zeros of sine are on the real axis. Hence, we suspect that a similar formula is needed to prove or disprove the Riemann hypothesis. However, it is not clear what this relation for ζ would be.
The Euler product of ζ which has been decisive [40] in the proofs of several weaker versions of the Riemann hypothesis might represent such a feature. However, we admit that at this point we do not yet see how to incorporate this aspect into our considerations.
In conclusion, we argue that the Newton flow of ζ represented either in the complex plane, or on the Riemann sphere might provide a fresh perspective on the Riemann hypothesis. Notwithstanding the fact that our technique has not yet provided an answer to this longstanding question we are still convinced that in the language of the American physicist John Archibald Wheeler it might well serve as 'an idea for an idea'.
Acknowledgments
We thank W Arendt, MV Berry, M Freyberger, MO Scully, A Wünsche and WH Zurek for many fruitful discussions. WPS is most grateful to Texas A & M University for a Texas A & M University Institute for Advanced Study (TIAS) Faculty Fellowship.
Appendix. Newton flow of sine function
In the main body of our article we argue that the properties of the Newton flow generated by the Riemann zeta function ζ provides insight into the Riemann hypothesis, that is into the claim that all non-trivial zeros are located on an axis in the complex plane. Our approach relies heavily on the asymptotic properties of ζ, that is on the behavior of ζ for large positive, or large negative real parts of the argument where ζ can be represented by rather elementary functions. However, the critical line with the non-trivial zeros is parallel to the imaginary axis at 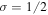 and is therefore close to the center of the complex plane rather than at infinity. Therefore, we are lead to the question: How can we expect to learn anything about the location of the non-trivial zeros by considering the asymptotics of ζ?
and is therefore close to the center of the complex plane rather than at infinity. Therefore, we are lead to the question: How can we expect to learn anything about the location of the non-trivial zeros by considering the asymptotics of ζ?
The example of the sine function discussed in this appendix is one where our counter-intuitive approach is successful and shares many similarities with the much more complicated problem of ζ. Indeed, it is well-known that all zeros of  are located on the real axis. Hence, the real axis is the critical line of
are located on the real axis. Hence, the real axis is the critical line of 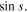 Moreover, due to the rotation of the critical axis by 90° compared to ζ the asymptotic behavior of ζ for large positive and negative real parts gets transformed for sine into large positive and negative imaginary parts. Finally, there is an analogue of the feature of ζ that due to its functional equation we have two rather than one non-trivial zeros asuming that the zero is not on the critical line. Indeed, if
Moreover, due to the rotation of the critical axis by 90° compared to ζ the asymptotic behavior of ζ for large positive and negative real parts gets transformed for sine into large positive and negative imaginary parts. Finally, there is an analogue of the feature of ζ that due to its functional equation we have two rather than one non-trivial zeros asuming that the zero is not on the critical line. Indeed, if  we obviously find
we obviously find  as well. Hence, s and its complex conjugate s* are zeros.
as well. Hence, s and its complex conjugate s* are zeros.
We now employ the Newton flow generated by the sine function and its asymptotic properties to verify that all zeros lie on the real axis. Our proof proceeds in three steps: (i) we first show that all flow lines start at positions in the complex plane with large positive and large negative imaginary parts with a vertical tangent. (ii) We then determine the phases of the separatrices which control the flow towards the zeros, and (iii) conclude by a proof by contradiction which shows that the zeros have to be on the real axis.
A.1. Asymptotics of the Newton flow
We start our discussion by first analyzing the asymptotics of the Newton flow of the sine function. Here we concentrate on two aspects: (i) the starting point at large positive and large negative imaginary parts of the argument  with vertical tangent, and (ii) the distribution of phases.
with vertical tangent, and (ii) the distribution of phases.
In the center of figure A1 we display the numerically obtained Newton flow
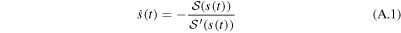
created by the sine function
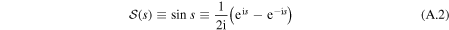
and its first derivative
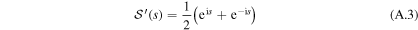
leading to
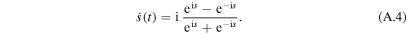
Due to the periodicity of  with period
with period 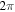 we confine ourselves in figure A1 to the interval
we confine ourselves in figure A1 to the interval 
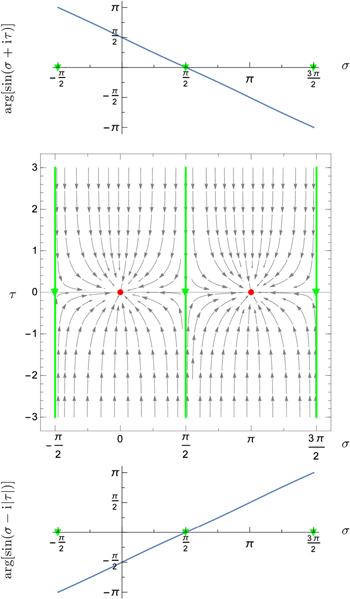
Figure A1. Proof that all zeros of the sine function 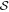 lie on the real axis solely based on the asymptotic properties of (i) the corresponding Newton flow represented in the complex plane (center), and (ii) the phases of the individual flow lines (top and bottom). At large positive and negative imaginary parts τ of the argument
lie on the real axis solely based on the asymptotic properties of (i) the corresponding Newton flow represented in the complex plane (center), and (ii) the phases of the individual flow lines (top and bottom). At large positive and negative imaginary parts τ of the argument  of
of 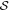 the flow lines are parallel to the imaginary axis and start towards the real axis. For large positive τ the phases decrease linearly with σ, whereas for large negative τ these phases increase. The well-known trigonometric relation
the flow lines are parallel to the imaginary axis and start towards the real axis. For large positive τ the phases decrease linearly with σ, whereas for large negative τ these phases increase. The well-known trigonometric relation  yields the phases
yields the phases 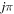 with
with 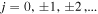 for the separatrices (green lines). In the interval
for the separatrices (green lines). In the interval  the phases of the flow lines cover a period of
the phases of the flow lines cover a period of 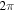 suggesting that there must be a simple zero in this domain. If this zero s0 would not lie on the real axis then not only would
suggesting that there must be a simple zero in this domain. If this zero s0 would not lie on the real axis then not only would 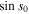 vanish, but also
vanish, but also 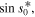 in contradiction to the asymptotic behavior of the flow lines which predicts one and not two zeros.
in contradiction to the asymptotic behavior of the flow lines which predicts one and not two zeros.
Download figure:
Standard image High-resolution imageThe flow originates exclusively from the top and the bottom of the figure and approaches the zeros which are indeed on the real axis. We emphasize that this figure is of course no proof but only serves as a guide for developing a proof. For this purpose we now verify analytically several features of this flow.
We start by noting that for 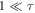 the flow, equation (A.4), reduces to the relation
the flow, equation (A.4), reduces to the relation
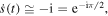
which shows that for large positive imaginary parts τ of s all flow lines, independent of the real part σ, have a vertical tangent and start towards the real axis.
Likewise, for large negative imaginary parts, that is for 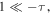 we obtain
we obtain

which indicates that independent of the real part σ the field lines have again a vertical tangent pointing towards the real axis.
We conclude this section by considering the phases of these flow lines. From the definition, equation (A.2), of  we obtain immediately the asymptotic representation
we obtain immediately the asymptotic representation
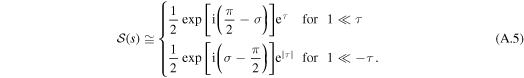
Hence, for the flow lines initiating from the top of the complex plane the phase decreases linearly as we increase τ, whereas for the ones originating from the bottom the phase increases linearly. This behavior of  is apparent in the top and the bottom parts of figure A1, respectively.
is apparent in the top and the bottom parts of figure A1, respectively.
A.2. Phases of separatrices
Next we turn to the phases of the separatrices which are determined by the phases of  at the points
at the points 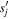 in the complex plane where
in the complex plane where 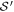 given by (A.3) vanishes. From the well-known trigonometric relation
given by (A.3) vanishes. From the well-known trigonometric relation

following from equations (A.2) and (A.3) we find with 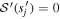 the condition
the condition
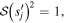
or
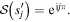
Hence, the phases of the separatrices are integer multiples j of π.
We emphasize that at this point we do not know the locations 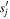 where
where  vanishes, but due to the trigonometric relation, equation (A.6), we could obtain the phases. Since they are constant along the whole flow line we can distinguish separatrices from regular flow lines by their phases at their starting points for large imaginary parts, that is at infinity.
vanishes, but due to the trigonometric relation, equation (A.6), we could obtain the phases. Since they are constant along the whole flow line we can distinguish separatrices from regular flow lines by their phases at their starting points for large imaginary parts, that is at infinity.
Indeed, from the asymptotic representation, equation (A.5), of  we find that the phases
we find that the phases  arise for
arise for
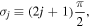
as indicated in the top and the bottom of figure A1 by green triangles.
Hence, in the interval 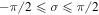 defined by two consecutive separatrices the phases of the flow lines originating from the top decrease linearly from π to zero. In contrast, the flow lines starting from the bottom increase linearly from
defined by two consecutive separatrices the phases of the flow lines originating from the top decrease linearly from π to zero. In contrast, the flow lines starting from the bottom increase linearly from  to zero. Hence, in this interval all flow lines cover a complete range of
to zero. Hence, in this interval all flow lines cover a complete range of  which indicates that this domain must include a simple zero.
which indicates that this domain must include a simple zero.
A.3. Proof by contradiction
We are now in the position to complete our proof based on the Newton flow that all zeros sj of 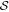 lie on the real axis. For this purpose we assume that there is one s0 that does not satisfy this property. In this case s0 has a non-vanishing imaginary part. However, the condition
lie on the real axis. For this purpose we assume that there is one s0 that does not satisfy this property. In this case s0 has a non-vanishing imaginary part. However, the condition
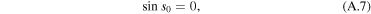
implies
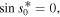
and thus the complex conjugate  of s0 is a zero as well.
of s0 is a zero as well.
Hence, we obtain two zeros, which is in contradiction with the prediction of a single zero due to the behavior of the Newton flow lines. As a consequence, the zero s0 has to lie on the real axis.
A.4. Comparison with ζ and outlook
We conclude by briefly comparing and contrasting the Newton flows of ζ and 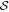 . Whereas in the introduction of this appendix we have emphasized the similarities, we now focus on the differences. Moreover, we identify the ingredient crucial for our proof of the distribution of zeros of
. Whereas in the introduction of this appendix we have emphasized the similarities, we now focus on the differences. Moreover, we identify the ingredient crucial for our proof of the distribution of zeros of  .
.
Obviously, the zeros of 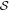 along the real axis play the role of the non-trivial zeros along the critical axis of ζ. However, due to the symmetry of
along the real axis play the role of the non-trivial zeros along the critical axis of ζ. However, due to the symmetry of 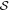 with respect to the real axis and the periodicity with a single period
with respect to the real axis and the periodicity with a single period  there are no trivial zeros of
there are no trivial zeros of  .
.
Moreover, we emphasize that it is this symmetry that enforces the Newton flow of 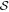 to approach the zeros from the top and the bottom of the complex plane. In contrast, the flow of ζ exclusively comes from the left and either goes straight to the non-trivial zeros, or passes them and eventually gets turned around by the separatrices at infinity.
to approach the zeros from the top and the bottom of the complex plane. In contrast, the flow of ζ exclusively comes from the left and either goes straight to the non-trivial zeros, or passes them and eventually gets turned around by the separatrices at infinity.
However, the most important difference between the Newton flows of  and ζ stands out in the asymptotic behavior of the phases and their grouping by the separatrices. Whereas in
and ζ stands out in the asymptotic behavior of the phases and their grouping by the separatrices. Whereas in  these phases decrease or increase linearly, in ζ the growth is faster due to the presence of the logarithm in equation (17).
these phases decrease or increase linearly, in ζ the growth is faster due to the presence of the logarithm in equation (17).
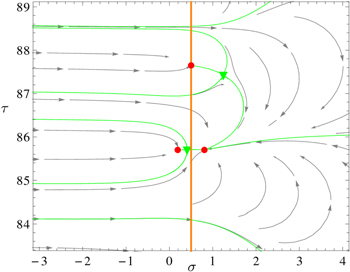
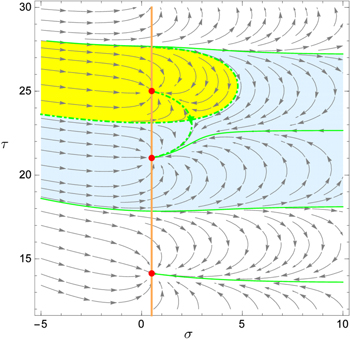
Moreover, the separation of the individual zeros by the separatrices is much more intricate in the case of ζ. Indeed, for  the phases of two consecutive separatrices always differ by π which is not the case for ζ as apparent from the second and third non-trivial zero of ζ depicted in figure 1 and amplified in figure A2
. Here the top green line consists of two separatrices that are rather close together: the one where ζ is real runs through the picture from the left to the right. The other one is slightly below and comes from the left but eventually turns around and approaches a zero of the derivative of ζ marked by a green triangle. The narrow path between these two separatrices leaves enough space for the flow in the light blue domain that needs to approach the second non-trivial zero from the right.
the phases of two consecutive separatrices always differ by π which is not the case for ζ as apparent from the second and third non-trivial zero of ζ depicted in figure 1 and amplified in figure A2
. Here the top green line consists of two separatrices that are rather close together: the one where ζ is real runs through the picture from the left to the right. The other one is slightly below and comes from the left but eventually turns around and approaches a zero of the derivative of ζ marked by a green triangle. The narrow path between these two separatrices leaves enough space for the flow in the light blue domain that needs to approach the second non-trivial zero from the right.
Figure A2. Nesting of the basins of attraction of the Newton flow of ζ illustrated for the first three non-trivial zeros of ζ. The flow (yellow) approaching the third non-trivial zero is embedded in the flow (light blue) moving towards the second zero.
Download figure:
Standard image High-resolution imageDue to this flow the phases of the flow lines caught between the lower separatrix going through the picture and the one approaching the hyperbolic point indicated in figure A2 by a green triangle cannot cover a complete interval of  Hence, in contrast to
Hence, in contrast to  where the flow domains in the complex plane are separated from each other, in ζ we find nested regions. For example, the domain (yellow region) for the third non-trivial zero is embedded in the region (light blue) of the second non-trivial zero as indicated in figure A2.
where the flow domains in the complex plane are separated from each other, in ζ we find nested regions. For example, the domain (yellow region) for the third non-trivial zero is embedded in the region (light blue) of the second non-trivial zero as indicated in figure A2.
We conclude by emphasizing that the crucial element of our proof for  was the trigonometric relation, equation (A.6), which allowed us to determine the phases of the separatrices without knowing the locations of the points where the first derivative vanishes. Unfortunately, at the moment we are not aware of an analogous relation for ζ.
was the trigonometric relation, equation (A.6), which allowed us to determine the phases of the separatrices without knowing the locations of the points where the first derivative vanishes. Unfortunately, at the moment we are not aware of an analogous relation for ζ.
Footnotes
- ☆
We dedicate this paper to the memory of Richard Lewis Arnowitt and his many contributions to general relativity and high energy physics.
- 6
'Man findet nun in der That etwa so viel reelle Wurzeln innerhalb dieser Grenzen, und es ist sehr wahrscheinlich, dass alle Wurzeln reell sind.'