Izvestiya: Mathematics

We prove a multiple coloured Tverberg theorem and a balanced coloured Tverberg theorem, applying different methods, tools and ideas. The proof of the first theorem uses a multiple chessboard complex (as configuration space) and the Eilenberg–Krasnoselskii theory of degrees of equivariant maps for non-free group actions. The proof of the second result relies on the high connectivity of the configuration space, established by using discrete Morse theory.

The intersection of two quadrics is called a biquadric. If we mark a non-singular quadric in the pencil of quadrics through a given biquadric, then the given biquadric is called a marked biquadric. In the classical papers of Plücker and Klein, a Kummer surface was canonically associated with every three-dimensional marked biquadric (that is, with a quadratic line complex provided that the Plücker–Klein quadric is marked). In Reid's thesis, this correspondence was generalized to odd-dimensional marked biquadrics of arbitrary dimension 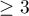$\ge 3$. In this case, a Kummer variety of dimension $g$ corresponds to every biquadric of dimension $2g-1$. Reid only constructed the generalized Plücker–Klein correspondence. This map was not studied later. The present paper is devoted to a partial solution of the problem of creating the corresponding theory.

We consider the problem of the optimal start control for two-dimensional Boussinesq equations describing non-isothermal flows of a viscous fluid in a bounded domain. Using the study of the properties of admissible tuples and of the evolution operator, we prove the solubility of the optimization problem under natural assumptions about the model data. We derive a variational inequality which is satisfied by the optimal control provided that the objective functional is determined by the final observation. We also obtain sufficient conditions for the uniqueness of an optimal control.

We construct an analogue of classical Lie theory in the case of Lie groups and Lie algebras defined over the algebra of dual numbers. As an application, we study approximate symmetries of differential equations and construct analogues of Hjelmslev's natural geometry.

It is well known that the number of homomorphisms from a group 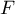$F$ to a group $G$ is divisible by the greatest common divisor of the order of $G$ and the exponent of $F/[F,F]$. We study the question of what can be said about the number of homomorphisms satisfying certain natural conditions like injectivity or surjectivity. 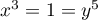A simple non-trivial consequence of our results is the fact that in any finite group the number of generating pairs $(x,y)$ such that $x^3=1=y^5$ is divisible by the greatest common divisor of fifteen and the order of the group $[G,G]\cdot\{g^{15}\mid g\in G\}$.