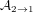Crossover from droplet to flat initial conditions in the KPZ equation from the replica Bethe ansatz

Recently there has been a lot of progress in finding exact solutions to the one-dimensional noisy Kardar–Parisi–Zhang (KPZ) equation. This equation [1] describes the growth of an interface, in the continuum, parameterized by its height field h(x, t) at point x and has numerous experimental realizations [2, 3]. The growth is generated by an additive space-time white noise, and the problem is to characterize the statistics of the height field as a function of time t. While the scaling exponents h ∼ t^1/3, x ∼ t^2/3 have been known for a while [4], the recent focus has been on the PDF (probability distribution function) of the height field. The KPZ problem can be mapped to the problem of a continuous directed polymer (DP) in a quenched random potential, in such a way that h(x, t) = lnZ(x, t) is proportional to the free energy of the DP with its endpoint at x and length t.

As was anticipated from exact solutions of discrete models which belong to the KPZ universality class, such as the PNG growth model [5]–[7], the TASEP particle transport model [8]–[10] or discrete DP models [11, 6], one expects only a few universal statistics at large time, depending on the type of initial condition. Remarkably, the interface retains some memory of the initial condition, even at large time.

For the KPZ equation on the infinite line there are three main classes. The droplet initial condition (which corresponds to a DP with two fixed endpoints) leads to height fluctuations governed at large time by the Tracy–Widom (TW) distribution F₂, the CDF (cumulative distribution function) of the largest eigenvalue of the GUE random matrix ensemble [12]. It has been solved simultaneously by two methods. The first route used a limit from an ASEP model with weak asymmetry [13] and allowed for a rigorous derivation [14, 15]. The second route [16, 17] used methods of disordered systems, namely replica ones, and methods from integrable systems, namely the Bethe ansatz ones. It works on the DP version and allows one to calculate the integer moments of Z = e^h from the known exact solution of the Lieb–Liniger delta Bose gas [18]. Extracting the PDF for h from the integer moments is, as yet, a non-rigorous step. For the droplet initial conditions, both methods obtained the CDF for all times t, in the form of a Fredholm determinant, nicely displaying convergence to F₂ as t → +∞.

The second important class, the flat initial condition, was solved using the replica Bethe ansatz (RBA) [19]–[21] in the form of a Fredholm Pfaffian, valid at all times. At large time the CDF of the height converges to the TW distribution F₁ associated with the GOE ensemble of random matrices. A rigorous derivation is only currently in progress [22]. In fact, remarkable developments have occurred in the mathematics community, from the study of the so-called q-TASEP and related models, which aim to produce many rigorous results as limit processes (e.g. as q → 1) [23]–[25].

The RBA also allowed for the solution of the last important class, the stationary KPZ [26], and of the KPZ equation on the half-line [27] which relates to the GSE random matrix ensemble. Note that all the above mentioned exact solutions arise due to an emerging, and somewhat miraculous, Fredholm determinant or Pfaffian structure, found to hold for arbitrary time. Another important aim is to use the RBA to derive systematically the large time asymptotics, even when the knowledge of the finite time result is unavailable. This strategy was recently explored, leading to another set of results [28]–[34]. The joint distribution of h(x, t) at several space points was obtained [29]–[32]. This is not strictly a 'new' result since from the PNG and TASEP models it was anticipated that the (scaled) many-point statistics of h(x, t) converge to those of the Airy₂ process ${\cal A}_2(x)$ (minus a parabola), whose one-point CDF is given by F₂. The Airy₂ process may be defined as the trajectory of the largest eigenvalue of the GUE Dyson Brownian motion (for a definition and review see e.g. [30, 9]; see also [35]). However, recovering this result within the RBA is a non-trivial and interesting result. Another breakthrough was the calculation within the RBA of the endpoint distribution of the DP [33] directly for infinite time, which was found to agree with the (simultaneous) result concerning the position of the maximum of the Airy 2 process (minus a parabola) [36]–[39]. In both cases, the corresponding finite time problem is unsolved and seems very difficult. A genuinely new result is the recent calculation from the RBA [34] of the two-time distribution for the KPZ equation at infinitely separated times. It is important to note that the manipulations leading directly to the infinite time limit in the RBA involve a substantial amount of 'guessing', which makes it even less rigorous. However, from the point of view of heuristics it is a very interesting route to explore further.

Besides these three main classes, one also expects three universal crossover classes (also called transition classes) with initial conditions which interpolate from one of the three classes at x = −∞ to a distinct one at x = +∞; see e.g. figure 4 in [15]. The aim of the present paper is to study the transition from GUE to GOE statistics in the KPZ equation. This is realized for the so-called 'half-flat' initial condition, which is flat to the left and droplet-like to the right. Interestingly, in [19, 20] we had already obtained the formula for the moments $\overline {Z^n}$ for the half-flat initial condition. There we studied only the x →−∞ limit of this formula to solve the flat case for arbitrary time. This formula seems hard to analyze for arbitrary time; however here we consider its large time limit and obtain the PDF for the KPZ height in the form of a Fredholm determinant interpolating between the F₂ and F₁ distributions. We obtain a new closed formula for the kernel and show that it is equivalent, via some Airy function identities, to the one obtained in appendix A of [41] from a solution of the TASEP. The corresponding Airy process was defined and characterized there and called ${\cal A}_{2 \to 1}$.

Since the recipe for the large time limit seems to work, we extend the calculation to obtain a genuinely new result. We consider the DP problem in the situation where each endpoint is free on its own half-line. It can again be solved in terms of Fredholm determinants, with new kernels. Recast in terms of Airy processes, it amounts to obtaining the distribution of the maximum of the transition process Airy_2→1 (minus a half-parabola) on a half-line.

The outline of the paper is as follows. In section 2 we recall the KPZ and DP models and their connection and define the dimensionless units. In section 3 we recall the known results for the droplet and the flat initial conditions. In section 4 we explain what we aim to do in this paper, give elementary facts about the transition process Airy_2→1 and introduce the generating function. In section 5 we briefly recall the replica Bethe ansatz method and in section 6, the formula from [19, 20]. In section 8 we consider the large time limit of this formula, and obtain the new form for the kernel of the transition process. In section 9 we use identities between Airy functions to put it in a form which is then compared in section 10 to the previous results of [41]. Finally in section 11 we generalize the problem, obtain the new kernels for the so-called LL and LR problems and explain the connection to the extrema of the Airy_2→1 process. We conclude on open problems and give some details in the appendices.

2.1. The KPZ equation

Consider the standard 1D continuum KPZ growth equation for the height field h(x, t):

$$\begin{eqnarray} &&\label {kpzeq} \partial _t h = \nu \nabla ^2 h + \tfrac {1}{2} \lambda _0 (\nabla h)^2 + \sqrt {D} \eta \end{eqnarray} \tag{ 1 }$$

in the presence of the white noise $\overline {\eta (x,t) \eta (x^{\prime },t^{\prime })}=\delta (x-x^{\prime }) \delta (t-t^{\prime })$. We define the scales

$$\begin{eqnarray}&&x_0 = (2 \nu )^3, \quad\qquad t_0 = 2 (2 \nu )^5 , \quad\qquad \lambda _0 h_0 = 2 \nu \end{eqnarray} \tag{ 2 }$$

and use them as units, i.e. we set x → x₀x, t → t₀t and h → h₀h and work from now on in the dimensionless units where the KPZ equation becomes

$$\begin{eqnarray} &&\label {kpzeq2} \partial _t h = \nabla ^2 h + (\nabla h)^2 + \sqrt {2 \bar c} ~ \eta \end{eqnarray} \tag{ 3 }$$

$$\begin{eqnarray} &&\bar c= D \lambda _0^2. \end{eqnarray} \tag{ 4 }$$

2.2. The directed polymer

Consider now Z(x, t|y, 0), the partition function of the continuum directed polymer in the random potential $- \sqrt {\bar c} ~ \eta (x,t)$ with fixed endpoints at (x, t) and (y, 0), at temperature T:

$$\begin{eqnarray} &&\label {zdef} Z(x,t|y,0) = \int _{x(0)=y}^{x(t)=x} {\rm D}x\, {\rm e} ^{- ({1}/{T}) \int _0^t {\rm d} \tau \, [({1}/{2}) ({{\rm d} x}/{{\rm d} \tau })^2 - \sqrt {\bar c} ~ \eta (x(\tau ),\tau ) ]}. \end{eqnarray} \tag{ 5 }$$

As is well known, it can be mapped onto the KPZ equation with the correspondence

$$\begin{eqnarray} &&\frac {\lambda _0}{2 \nu } h \equiv \ln Z , \quad\qquad T=2 \nu . \end{eqnarray} \tag{ 6 }$$

Here and below, overbars denote averages over the white noise η. For both problems we define, as in [16, 17, 19], the dimensionless parameter ∼t^1/3:

$$\begin{eqnarray} &&\label {lambdadef} \lambda = \tfrac {1}{2} (\bar c^2 t/T^5)^{1/3} , \end{eqnarray} \tag{ 7 }$$

which measures the scale of the fluctuations of the DP free energy, i.e. of the KPZ height. From now on we use the same units x₀ = T³ and t₀ = 2T⁵ as above, and in these dimensionless units the partition sum Z = Z(x, t|y, 0) is the solution of

$$\begin{eqnarray} &&\label {dp1} \partial _t Z = \nabla ^2 Z + \sqrt {2 \bar c} ~ \eta Z \end{eqnarray} \tag{ 8 }$$

with initial condition Z(x = 0, t|y, 0) = δ(x − y). In these units the dimensionless parameter is $\lambda =(\bar c^2t/4)^{1/3}$.

2.3. The Cole–Hopf mapping

The Cole–Hopf mapping solves the KPZ equation in terms of the DP partition sum, in the dimensionless units:

$$\begin{eqnarray} &&{\rm e} ^{h(x,t)} = \int {\rm d} y\, Z(x,t|y,0) {\rm e} ^{h(y,t=0)}. \end{eqnarray} \tag{ 9 }$$

which maps equation (3) into (8). We will thus also adopt the notation

$$\begin{eqnarray} &&\label {drop0} h(x,t|y,0) = \ln Z(x,t|y,0), \end{eqnarray} \tag{ 10 }$$

although it is somewhat improper since it requires a regularization near t = 0 (see below).

Below, when specified, we will often set $\bar c=1$ which amounts to the further change of units $x \to x/\bar c$ and $t \to t/\bar c^2$.

The droplet initial conditions for the KPZ equation is by definition the narrow wedge

$$\begin{eqnarray}&&h_{\rm drop}(x,t=0)= - w |x|, \quad\qquad w \to + \infty \end{eqnarray} \tag{ 11 }$$

and corresponds to the fixed endpoint initial condition Z(x, t = 0) = δ(x) for the DP. More generally, h(x, t|y, 0) ≡ h_drop(x − y, t) + ln(w/2) given by (10) corresponds to a sharp wedge centered at y. Everywhere in this paper ≡ means equivalent in law. The additive constant ln(w/2) is necessary for regularization, but we will ignore below all time-independent constants.

It is known [13]–[17] that at large time the one-point fluctuations of the height grow as t^1/3 and are governed by the GUE Tracy–Widom (cumulative) distribution F₂(s) as

$$\begin{eqnarray} &&\label {defxi} h_{\rm drop}(0,t) = \ln Z_{\rm drop}(0,t) \simeq v_0 t + \bar c^{2/3} t^{1/3} \chi _2 \end{eqnarray} \tag{ 12 }$$

$$\begin{eqnarray} &&{\rm Prob}(\chi _2 < s) = F_2(s) = {\rm Det}[I - P_0 K^s_{{Ai}} P_0] \end{eqnarray} \tag{ 13 }$$

where F₂(s) is given by a Fredholm determinant with the Airy kernel

$$\begin{eqnarray} &&\label {airyK} K_{{Ai}}^s(v_1,v_2)= K_{{Ai}}(v_1+s,v_2+s) , \quad\qquad K_{{Ai}}(v,v^{\prime })= \int _{y>0} {\rm d} y\, {Ai}(y+v) {Ai}(y+v^{\prime }) \end{eqnarray} \tag{ 14 }$$

and P₀(v) = θ(v) is the projector on R⁺.

More generally, for droplet initial conditions, the multi-point correlation is believed to converge [30, 15, 42] to the ones of the Airy₂ process ${\cal A}_2(u)$  [6, 9] with (in units¹ where $\bar c=1$):

$$\begin{eqnarray} &&\label {h2} h(x,t) \simeq v_0 t + t^{1/3} ({\cal A}_2(u) - u^2 ), \quad\qquad u=\frac {x}{2 t^{2/3}} \end{eqnarray} \tag{ 15 }$$

where ${\cal A}_2(0) \equiv \chi _2$ and the process ${\cal A}_2(u)$ is stationary, i.e. statistically translationally invariant in u.

For the flat initial condition h(x, t = 0) = 0, it was found [19, 20] that²:

$$\begin{eqnarray}&&h_{\rm flat}(0,t) = \ln Z_{\rm flat}(0,t) = v_0 t + \bar c^{2/3} 2^{-2/3} t^{1/3} \chi _1 \end{eqnarray} \tag{ 16 }$$

$$\begin{eqnarray} &&{\rm Prob}(\chi _1 < s) = F_1(s) = {\rm Det}[1 - P_0 B_s P_0] \end{eqnarray} \tag{ 17 }$$

where F₁(s) is the GOE Tracy–Widom (cumulative) distribution which is expressed as a Fredholm determinant with the kernel B_s(v, v') = Ai(v + v' + s). Again it is believed that in that case the joint distributions of the heights {h_flat(x, t)}_x are governed by the so-called Airy₁ stationary process ${\cal A}_1(u)$ (switching back to units where $\bar c=1$):

$$\begin{eqnarray}&&h(x,t) \simeq v_0 t + 2^{1/3} t^{1/3} {\cal A}_1(2^{-2/3} u) \end{eqnarray} \tag{ 18 }$$

where ${\cal A}_1(0) = \frac {1}{2} \chi _1$. For the definition and normalizations of the Airy₁ process see e.g. [10, 9, 39], and for its (lack of) connection to the GOE Dyson Brownian motion (beyond the one-point distribution), see [40].

Note that there is a connection between these results. Indeed from the definition one expects, in the large time limit,

$$\begin{eqnarray} &&h_{\rm flat}(x,t) = \ln \int {\rm d} y \, {\rm e} ^{h(x,t|y,0)} \equiv \ln \int {\rm d} y\, {\rm e} ^{h(y,t|x,0)} \simeq v_0 t + t^{1/3} \max _u ({\cal A}_{2}(u) - u^2) \end{eqnarray} \tag{ 19 }$$

where we have used that the sets {h(x, t|y, 0)}≡{h(y, t|x, 0)} are statistically equivalent and that, since height fluctuations grow as t^1/3, the integral is dominated by the maximum. Hence,

$$\begin{eqnarray} &&\max _u ({\cal A}_2(u) - u^2) = 2^{-2/3} \chi _1 = 2^{1/3} {\cal A}_1(0), \end{eqnarray} \tag{ 20 }$$

i.e. the maximum of the Airy₂ process minus a parabola is given by the Airy₁ process at one point, as proved in [39].

4.1. Half-flat initial conditions and the STS identity

Consider the double-wedge initial condition for the KPZ field on the real axis:

$$\begin{eqnarray}&&h(x,t=0)= w x ~ \theta (-x) - w^{\prime } x ~ \theta (x) \label {wedgeic} \end{eqnarray} \tag{ 21 }$$

where θ(x) is the Heaviside step function. In this paper we focus on the limit w'→ +∞. In terms of the DP it corresponds to a (left) half-space problem with partition sum

$$\begin{eqnarray} &&\label {hsdef} h_w(x,t)= \ln Z_{w}(x,t) \end{eqnarray} \tag{ 22 }$$

$$\begin{eqnarray}&&Z_{w}(x,t) = \int _{-\infty }^{0} {\rm d} y\, {\rm e} ^{w y} Z(x,t|y,0), \end{eqnarray} \tag{ 23 }$$

with Z_w(x, t = 0) = θ(−x)e^wx. Hence for w = 0 it can be seen as a 'half-flat' initial condition; see figure 1.

Zoom In Zoom Out Reset image size

Our aim here is to calculate the one-point probability distribution (PDF) of (minus) the free energy of the DP, or equivalently, of the height field of the KPZ equation. We write

$$\begin{eqnarray} &&\label {defxi} -F = h = \ln Z = v_0 t + \lambda \xi _t , \quad\qquad Z \equiv Z_{w}(x,t) , \quad \lambda = (\bar c^2 t/4)^{1/3} \end{eqnarray} \tag{ 24 }$$

which defines ξ_t. This is done by calculating via the Bethe ansatz the integer moments of the partition function $\overline {Z^n}$. Using the statistical tilt symmetry (STS) of the problem it is easy to show the exact relation for integer moments (see e.g. [19] appendix A):

$$\begin{eqnarray} &&\label {stsrel} \overline {Z^n_w(x,t)} = {\rm e} ^{-{n x^2}/{4 t}} \overline {Z^n_{w+{x}/{2 t}}(0,t)} \end{eqnarray} \tag{ 25 }$$

or equivalently

$$\begin{eqnarray} &&\label {sts1} \ln Z_w(x,t) + \frac {x^2}{4 t} \equiv _{\rm in ~ law} \ln Z_{w+{x}/{2 t}}(0,t). \end{eqnarray} \tag{ 26 }$$

Hence, up to a simple additive piece in the free energy, the problem depends only on the combination w + x/2t, i.e. changing the endpoint is the same as changing w. Since we know that h₀(−∞, t) ≡ h_flat(0, t) and h_+∞(0, t) ≡ h_drop(0, t) there are thus two limits:

$$\begin{eqnarray}&&w + \frac {x}{2 t} \to + \infty , \quad\qquad h_{w+{x}/{2 t}}(0,t) \equiv h_{\rm drop}(0,t) \end{eqnarray} \tag{ 27 }$$

$$\begin{eqnarray}&&w + \frac {x}{2 t} \to - \infty , \quad\qquad h_{w+{x}/{2 t}}(0,t) \equiv h_{\rm flat}(0,t); \end{eqnarray} \tag{ 28 }$$

hence the present problem extrapolates from droplet to flat initial conditions.

4.2. The relation to the ${\cal A}_{2\to 1}$ transition process

Although this crossover has not yet been fully studied for the KPZ equation, it has been studied in [41] for the TASEP with an initial condition where particles are placed at the even integers, the equivalent of the 'half-flat' initial condition. There the transition process ${\cal A}_{2 \to 1}(u)$ was defined. It enjoys the two limits³

$$\begin{eqnarray} &&\lim _{u_1 \to + \infty } {\cal A}_{2 \to 1}(u + u_1) = 2^{1/3} {\cal A}_1 (2^{-2/3} u) \end{eqnarray} \tag{ 29 }$$

$$\begin{eqnarray} &&\lim _{u_1 \to - \infty } {\cal A}_{2 \to 1}(u + u_1) = {\cal A}_2(u). \end{eqnarray} \tag{ 30 }$$

It was later shown [39] that this transition process satisfies

$$\begin{eqnarray} &&\max _{v < u} ({\cal A}_2(v)-v^2) + \min (0,u)^2 = {\cal A}_{2 \to 1}(u). \end{eqnarray} \tag{ 31 }$$

It is then clear that the crossover studied here in the KPZ equation should be related to this transition process in the limit of infinite time. Indeed, let us generalize our notation slightly and define

$$\begin{eqnarray}&&h^L_{zw}(x,t) = \ln \int _{y < z} {\rm d} y \, {\rm e} ^{h(x,t|y,0)+w y}, \end{eqnarray} \tag{ 32 }$$

so that $h_w(x,t)=h^L_{0w}(x,t)$. Then we again expect that in the large time limit this solution will be related to the maximum of the droplet solution on a half-line⁴

$$\begin{eqnarray} &&h^L_{z0}(x,t) = \ln \int _{y < z} {\rm d} y\, {\rm e} ^{h(x,t|y,0)} \equiv \ln \int _{y < z} {\rm d} y\, {\rm e} ^{h(y,t|x,0)}\nonumber \\ &&\simeq _{t \to \infty } \max _{y<z} h(y,t|x,0) \equiv \max _{y<z-x} h_{\rm drop}(y,t). \end{eqnarray} \tag{ 33 }$$

From (15) one then sees that (in units $\bar c=1$)

$$\begin{eqnarray} &&h^L_{z}(x,t) \simeq _{t \to \infty } t^{1/3} \max _{v < ({z-x})/{2 t^{2/3}}} ({\cal A}_2(v) - v^2 ) = t^{1/3} [{\cal A}_{2 \to 1}(u) - \min (0,u)^2 ]_{u=({z-x})/{2 t^{2/3}}}. \label {hLAiry} \end{eqnarray} \tag{ 34 }$$

More generally,

$$\begin{eqnarray} &&h^L_{zw}(x,t) \simeq _{t \to \infty } \max _{y<z} (h(y,t|x,0) + w y) \equiv w x + \max _{y<z-x} (h_{\rm drop}(y,t) + w y) \end{eqnarray} \tag{ 35 }$$

$$\begin{eqnarray} &&= w x + t^{1/3} \max _{2 t^{2/3} v < z-x} (- v^2 + {\cal A}_2(v) + 2^{2/3} \tilde w \times 2 v ) \end{eqnarray} \tag{ 36 }$$

$$\begin{eqnarray} &&\equiv - \frac {x^2}{4 t} + t \left (w + \frac {x}{2 t}\right )^2 + \max _{v < u} (- v^2 + {\cal A}_2(v) ) \end{eqnarray} \tag{ 37 }$$

$$\begin{eqnarray} &&= - \frac {x^2}{4 t} + t \left (w + \frac {x}{2 t}\right )^2 + t^{1/3} [{\cal A}_{2 \to 1}(u) - \min (0,u)^2 ]_{u=- t^{1/3} (w + ({x-z})/{2 t})} \label {resa21} \end{eqnarray} \tag{ 38 }$$

where we have defined the scaled variable $\tilde w = \lambda w$ and used the stationarity of ${\cal A}_2$ to shift its argument. We also note that the last line can be rewritten as

$$\begin{eqnarray}&&h^L_{zw}(x,t) \simeq _{t \to \infty } = h^{L0}_{zw}(x,t) + t^{1/3} {\cal A}_{2 \to 1}(u) \end{eqnarray} \tag{ 39 }$$

where $h^{(L0)}_{zw}(x,t) = \max _{y<z} (-{(y-x)^2}/{4 t} + w y)$ is the large time solution of the KPZ equation with the same initial conditions, in the absence of noise. This shows why the term −min(0, u)² has been included in the definition of the transition Airy process chosen in [41].

4.3. The generating function and its large time limit

To later extract the PDF from the moments we now introduce the generating function, as in our previous works [16, 19, 20]:

$$\begin{eqnarray} &&\label {defg} g_\lambda (s) = \overline {{\rm e} ^{- {\rm e} ^{- \lambda s} Z_{w}(x,t)}} = 1 + \sum _{n=1}^\infty \frac {(- {\rm e} ^{- \lambda s})^n}{n!} \overline {Z_{w}(x,t)^n} = \overline { \exp (- {\rm e} ^{- \lambda (s - \xi )} ) }. \end{eqnarray} \tag{ 40 }$$

Once g_λ(s) is known, the PDF of (minus) the rescaled free energy, P(ξ), at large time (i.e. λ →∞) is immediately extracted as

$$\begin{eqnarray} &&\label {conv} g_{\infty }(s) = \lim _{\lambda \to \infty } g_\lambda (s) = \overline { \theta (s-\xi ) } = {\rm Prob}(\xi < s) . \end{eqnarray} \tag{ 41 }$$

Here we will calculate the generating function g_+∞(s) for the half-flat initial condition using the replica Bethe ansatz. We will check that it does reproduce correctly the two limits:

$$\begin{eqnarray}&&w + \frac {x}{2 t} \to + \infty , \quad\qquad g_\infty (s) = \lim _{t \to \infty } {\rm Prob}(\xi _t < s) = F_2(2^{-2/3} s) \end{eqnarray} \tag{ 42 }$$

$$\begin{eqnarray}&&w + \frac {x}{2 t} \to - \infty , \quad\qquad g_\infty (s) = \lim _{t \to \infty } {\rm Prob}(\xi _t < s) = F_1(s) , \end{eqnarray} \tag{ 43 }$$

in terms of the scaled random variable ξ_t defined in (24), where F₁(s) and F₂(s) are respectively the GOE and GUE Tracy–Widom distributions.

The calculation of the nth integer moment of the DP partition sum can be expressed [43, 44] using the eigenstates Ψ_μ and eigenenergies E_μ of the attractive Lieb–Liniger Hamiltonian for n bosons [18]:

$$\begin{eqnarray}&&H_n = -\sum _{\alpha =1}^n \frac {\partial ^2}{\partial {x_\alpha ^2}} - 2 \bar c \sum _{1 \leq \alpha < \beta \leq n} \delta (x_\alpha - x_\beta ), \label {LL} \end{eqnarray} \tag{ 44 }$$

namely⁵ [19],

$$\begin{eqnarray} &&\overline {Z_{w}(x,t)^n}= \sum _\mu \frac {\Psi ^*_\mu (x,\ldots ,x)}{\Vert \mu \Vert ^2} {\rm e} ^{-t E_\mu } \Bigg (\prod _{\alpha =1}^n \int _{-\infty }^0 {\rm d} y_\alpha \, {\rm e} ^{w y_\alpha } \Bigg ) \Psi _\mu (y_1\cdots y_n). \label {sumf} \end{eqnarray} \tag{ 45 }$$

These eigenstates are known from the Bethe ansatz [18]. They are parameterized by a set of rapidities μ ≡{λ₁, ..., λ_n} which are solutions of a set of coupled equations, the Bethe equations (see below). They take the (unnormalized) form (totally symmetric in the x_α):

$$\begin{eqnarray} &&\label {def1} \Psi _\mu (x_1,\ldots ,x_n) = \sum _P A_P \prod _{j=1}^n {\rm e} ^{{\rm i} \sum _{\alpha =1}^n \lambda _{P_\alpha } x_\alpha } , \quad\qquad A_P=\prod _{n \geq \beta > \alpha \geq 1} \Biggl (1 + \frac {{\rm i} \bar c\, {\mathrm {sgn}}(x_\beta - x_\alpha )}{\lambda _{P_\beta } - \lambda _{P_\alpha }}\Biggr ) \end{eqnarray} \tag{ 46 }$$

where the sum runs over all n! permutations P of the rapidities λ_j. The corresponding eigenenergies are $E_\mu =\sum _{\alpha =1}^n \lambda _\alpha ^2$. In the formula (45) we also need

$$\begin{eqnarray} &&\Psi ^*_\mu (x,\ldots ,x) = n! {\rm e} ^{- {\rm i} x \sum _\alpha \lambda _\alpha } . \label {Psixeq} \end{eqnarray} \tag{ 47 }$$

Before discussing the last two ingredients in (45), i.e. the norms ∥μ∥² and the half-space integrals of the Bethe eigenfunctions, let us recall the spectrum of H_n in the limit of infinite system size, i.e. the rapidities solution to the Bethe equations [45]. A general eigenstate is built by partitioning the n particles into a set of n_s ≤ n bound states called strings formed of m_j ≥ 1 particles with $n=\sum _{j=1}^{n_{\rm s}} m_j$. The rapidities associated with these states are written as

$$\begin{eqnarray}&&\label {stringsol} \lambda ^{j, a}=k_j +\frac {{\rm i} \bar {c}}2(m_j+1-2a). \end{eqnarray} \tag{ 48 }$$

Here, a = 1, ..., m_j labels the rapidities within the string j = 1, ..., n_s. Inserting these in (46) leads to the Bethe eigenstates of the infinite system, and their corresponding eigenenergies:

$$\begin{eqnarray} &&\label {en} E_\mu = \sum _{j=1}^{n_{\rm s}} m_j k_j^2-\frac {\bar {c}^2}{12} m_j(m_j^2-1). \end{eqnarray} \tag{ 49 }$$

For now on, we use units where $\bar c=1$. The calculation of the norms is involved. The result however is simple: in the large system size L limit, it can be written as [46]

$$\begin{eqnarray} &&\frac {1}{\Vert \mu \Vert ^2} = \frac {1}{n! L^{n_{\rm s}} } \prod _{1\leq i<j\leq n_{\rm s}} \Phi _{k_i,m_i,k_j,m_j} \prod _{j=1}^{n_{\rm s}} \frac 1{m_j^{2}} , \quad\qquad \Phi _{k_i,m_i,k_j,m_j}=\frac {4(k_i-k_j)^2 +(m_i-m_j)^2}{4(k_i-k_j)^2 +(m_i+m_j)^2}. \nonumber \\ &&\label {norm} \end{eqnarray} \tag{ 50 }$$

Consider now the integral in (45) over the negative half-space. Since the wavefunctions are totally symmetric in their arguments, it can be performed on the sector y₁ < y₂ < ⋯ < y_n < 0. Using that

$$\begin{eqnarray*} &&G_{\lambda } = \int _{-\infty < y_1<y_2< \cdots <y_n < 0} {\rm d} y_1\cdots {\rm d} y_n\, {\rm e} ^{\sum _{\alpha =1}^n (w+ {\rm i} \lambda _\alpha ) y_\alpha } = \prod _{j=1}^{n} \frac {1}{ j w + {\rm i} \lambda _1 + \cdots + {\rm i} \lambda _j }, \end{eqnarray*}$$

a 'miracle' occurs upon performing the summation over the permutations, leading to the factorized form [19, 20]

$$\begin{eqnarray} &&\Bigg (\prod _{\alpha =1}^n \int _{-\infty }^0 {\rm d} y_\alpha \, {\rm e} ^{w y_\alpha } \Bigg ) \Psi _\mu (y_1\cdots y_n) = \sum _P A_P G_{P \lambda } \nonumber \\ &&= \frac {n!}{ \prod _{\alpha =1}^n (w+ {\rm i} \lambda _\alpha )} \prod _{1 \leq \alpha < \beta \leq n} \frac {2 w + {\rm i} \lambda _\alpha + {\rm i} \lambda _\beta - 1}{ 2 w+ {\rm i} \lambda _\alpha + {\rm i} \lambda _\beta } . \label {miracle} \end{eqnarray} \tag{ 51 }$$

Let us now explain a point which was implicit in [19, 20]. Note that, strictly, (51) is valid only for Re(jw + iλ₁ + ⋯ + iλ_j) > 0 for all j. Hence (51), which involves all G_Pλ, is valid a priori when all λ_j are real and w > 0. However, one easily sees that its validity is more general. An important property of Ψ_μ for a string state is that A_P = 0 (for x₁ < ⋯ < x_n) unless the imaginary parts of the rapidities belonging to a given string are in increasing order. For instance for n₂ = 2, m₁ = 2, m₂ = 3, A_P is non-zero only for (λ₁, ..., λ₅) obtained from $(k_1-{{\rm i} \bar c}/{2},k_1+{{\rm i} \bar c}/{2},k_2- {3 {\rm i} \bar c}/{2},k_2-{{\rm i} \bar c}/{2},k_2+{{\rm i} \bar c}/{2},k_2+{3 {\rm i} \bar c}/{2})$ by a permutation of S₅ which respects the order of the imaginary parts inside each string (e.g. $k_1-{{\rm i} \bar c}/{2}$ must always appear before $k_1+{{\rm i} \bar c}/{2}$). From this it is easy to see that the condition Re(jw + iλ_P1 + ⋯ + iλ_Pj) > 0 for all j is satisfied for all terms with non-zero A_P. Physically it just expresses the fact that the bound states have a convergent integral over space, and w > 0 is needed only to make the integral over the center of mass convergent.

Let us recall the derivation in [19, 20], as it will be needed for further generalizations. From the ingredients (47), (49), (50), (51) we can now perform the summation ∑ _μ over the eigenstates in (45). It factors into a sum over the string variables k_j, m_j. One shows that in the infinite system the string momenta m_jk_j are quantized as free particles; hence we can make the replacement ∑ _kj → m_jL∫ (dk_j/2π), and all factors L cancel with the norms. One obtains the moments $\overline {Z^n}$ as a sum (m₁, ..., m_ns)_n over all the partitioning of n:

$$\begin{eqnarray} &&\label {startZ} \overline {Z^n} = \sum _{n_{\rm s}=1}^n \frac {n! 2^n}{n_{\rm s}!} \sum _{(m_1,\ldots ,m_{n_{\rm s}})_n} \prod _{j=1}^{n_{\rm s}} \int \frac {{\rm d} k_j}{2 \pi } \frac {1}{m_j} {\rm e} ^{m_j^3 ({t}/{12})- m_j k_j^2 t - {\rm i} x m_j k_j } \Phi [k,m] S^w[k,m] D^w[k,m] \end{eqnarray} \tag{ 52 }$$

together with the generating function as an expansion in the number of strings:

$$\begin{eqnarray} &&g_\lambda (s) = 1 + \sum _{n_{\rm s}=1}^\infty \frac 1{n_{\rm s}!} Z(n_{\rm s},s) \end{eqnarray} \tag{ 53 }$$

$$\begin{eqnarray} &&Z(n_{\rm s},s) = \sum _{m_1,\ldots , m_{n_{\rm s}}=1}^\infty \prod _{j=1}^{n_{\rm s}} \frac {2^{m_j}}{m_j}\nonumber \\ &&\times \ \int \frac {{\rm d} k_j}{2 \pi } S^w_{m_j,k_j} {\rm e} ^{m_j^3 ({t}/{12})- m_j k_j^2 t - \lambda m_j s - {\rm i} x m_j k_j} \prod _{1 \leq i < j \leq n_{\rm s}} \tilde D^w_{m_i,k_i,m_j,k_j} \label {start} \end{eqnarray} \tag{ 54 }$$

In g_λ(s) the summations over the m_j are free. The factors S^w and D^w are obtained by inserting the string rapidities (48) into (51). They read

$$\begin{eqnarray} &&\label {sw} S^w_{m,k} = \frac {(-1)^m \Gamma (z)}{\Gamma (z + m)} , \quad\qquad z= 2 {\rm i} k + 2 w. \end{eqnarray} \tag{ 55 }$$

and

$$\begin{eqnarray} &&\label {dw} D^w_{m_1,k_1,m_2,k_2} = \frac {\Gamma \left (1-z -({m_1+m_2})/{2}\right ) \Gamma \left (1-z +({m_1+m_2})/{2}\right ) }{ \Gamma \left (1-z +({m_1-m_2})/{2}\right ) \Gamma \left (1-z -({m_1-m_2})/{2}\right )}\end{eqnarray} \tag{ 56 }$$

$$\begin{eqnarray} &&= (-1)^{m_2} \frac {\Gamma (1- z + ({m_1+m_2})/{2}) \Gamma (z + ({m_1-m_2})/{2}) }{ \Gamma (1- z + ({m_1-m_2})/{2}) \Gamma (z + ({m_1+m_2})/{2})} ,\nonumber \\ &&z= {\rm i} k_1+{\rm i} k_2 + 2 w \label {dw2} \end{eqnarray} \tag{ 57 }$$

and in (52), (54) we have defined the notation

$$\begin{eqnarray} &&\tilde D^w_{m_i,k_i,m_j,k_j} = D^w_{m_i,k_i,m_j,k_j} \Phi _{k_i,m_i,k_j,m_j} , \quad\qquad S^w[k,m]= \prod _{j=1}^{n_{\rm s}} S^w_{m_j,k_j} \end{eqnarray} \tag{ 58 }$$

$$\begin{eqnarray}&&D^w[k,m]= \prod _{1 \leq i < j \leq n_{\rm s}} D^w_{m_i,k_i,m_j,k_j} , \quad\qquad \Phi [k,m]= \prod _{1 \leq i < j \leq n_{\rm s}} \Phi _{k_i,m_i,k_j,m_j} \end{eqnarray} \tag{ 59 }$$

involving the factor (50) coming from the norm. Note that we have also performed the shift $Z \to Z {\rm e} ^{\bar c^2 t/12}$ which yields the factor $-\bar c^2/12$ in v₀ in section 3.

Two remarks are in order:

(i) The STS relation (25) between moments can be retrieved by performing a change of integration variable in the integral (54):

$$\begin{eqnarray} &&{\rm i} k_j \to {\rm i} k_j + \frac {x}{2 t} \end{eqnarray} \tag{ 60 }$$

resulting in the global shift Z(n_s, s)|_{x, w} → Z(n_s, s)|_{0, w'}e^{−(x2/4t) ∑_jm_j} with a new value w → w' = w + x/2t. Since we know that this STS relation holds, this shift (followed by shifting the integration contour back to the real axis) must be legitimate provided w' = w + (x/2t) > 0 since this is the assumption used to derive (54).

(ii) While the formula for the moments $\overline {Z^n}$ is well defined, because of the exponential cubic divergence of the series, the formula (54) should be taken in some analytical continuation sense, i.e. it is valid as a formal series in t. One way to do that, as discussed in [16, 17] and below, is to use the Airy trick, valid for Re(z) > 0:

$$\begin{eqnarray} &&\label {airytrick} \int _{-\infty }^\infty {\rm d} y\, {Ai}(y) {\rm e} ^{y z} = {\rm e} ^{z^3/3}, \end{eqnarray} \tag{ 61 }$$

the summations over m being then carried later at fixed y and usually convergent.

Let us first perform some rescaling and rearrangement of our starting expression, to make taking the large time limit in section 8 easier. In the $\bar c=1$ dimensionless units, one has t = 4λ³. One can the define the scaled position and slope:

$$\begin{eqnarray}&&w = \frac {\tilde w}{\lambda }=\frac {\tilde w}{(t/4)^{1/3}} , \quad\qquad x=\lambda ^2 \tilde x = (t/4)^{2/3} \tilde x \end{eqnarray} \tag{ 62 }$$

such that $\tilde w$ and $\tilde x$ will be kept finite in the large time limit. One then performs the change k_j → k_j/λ in the integral. We get

$$\begin{eqnarray} &&Z(n_{\rm s},s) = \prod _{j=1}^{n_{\rm s}} \sum _{m_j=1}^{+\infty } \frac {2^{m_j}}{\lambda m_j} \int \frac {{\rm d} k_j}{2 \pi } \frac {(-1)^{m_j} \Gamma (({2 {\rm i} k_j + 2 \tilde w})/{\lambda })}{\Gamma (({2 {\rm i} k_j + 2 \tilde w})/{\lambda } + m_j)} {\rm e} ^{({1}/{3}) \lambda ^3 m_j^3 - 4 \lambda m_j k_j^2 - \lambda m_j s - {\rm i} \lambda m_j k_j \tilde x} \nonumber \\ &&\times \ \prod _{1 \leq i < j \leq n_{\rm s}} D^w_{m_i,k_i/\lambda ,m_j,k_j/\lambda } \frac {4(k_i-k_j)^2 +\lambda ^2 (m_i-m_j)^2}{4(k_i-k_j)^2 +\lambda ^2 (m_i+m_j)^2}. \label {startresc} \end{eqnarray} \tag{ 63 }$$

An equivalent expression is obtained using the Airy trick and the double Cauchy identity:

$$\begin{equation*} \prod _{1 \leq i < j \leq n_{\rm s}} \frac {4(k_i-k_j)^2 +\lambda ^2 (m_i-m_j)^2}{4(k_i-k_j)^2 +\lambda ^2 (m_i+m_j)^2} = {\rm det}\Bigg [\frac {1}{ 2 {\rm i} (k_i - k_j) + \lambda m_i + \lambda m_j }\Bigg ]_{n_{\rm s} \times n_{\rm s}} \prod _{j=1}^{n_{\rm s}} (2 \lambda m_j) \end{equation*}$$

followed by the shift $y_j \to y_j + s+ 4 k_j^2$, which leads to

$$\begin{eqnarray} &&Z(n_{\rm s},s) = \prod _{j=1}^{n_{\rm s}} \sum _{m_j=1}^{+\infty } 2^{m_j+1} \int \frac {{\rm d} k_j}{2 \pi } \,{\rm d} y_j\, \frac {(-1)^{m_j} \Gamma (({2 {\rm i} k_j + 2 \tilde w})/{\lambda })} {\Gamma (({2 {\rm i} k_j + 2 \tilde w})/{\lambda } + m_j)}\nonumber \\ &&\times \ {Ai}(y_j+ 4 k_j^2 + s) {\rm e} ^{\lambda m_j (y_j - i k_j \tilde x) } \prod _{1 \leq i < j \leq n_{\rm s}} D^w_{m_i,k_i/\lambda ,m_j,k_j/\lambda }\nonumber \\ &&\times \ {\rm det}\left [\frac {1}{ 2 {\rm i} (k_i - k_j) + \lambda m_i + \lambda m_j }\right ]_{n_{\rm s} \times n_{\rm s}}. \label {2} \end{eqnarray} \tag{ 64 }$$

Note that we know from the STS relation (26) that g(s) only depends on the following combination of variables:

$$\begin{eqnarray} &&\label {gsts} g_\lambda (s;w,x) = \tilde g_\lambda \left (s + \frac {\tilde {x}^2}{16} , \tilde w + \frac {\tilde x}{8} \right ). \end{eqnarray} \tag{ 65 }$$

We now study the limit of large time, i.e. λ → +∞. We will now assume that in this limit we can set the complicated factor $D^w_{m_i,k_i/\lambda ,m_j,k_j/\lambda }$ to 1, which we do from now on. This appears to be true a posteriori from the result that we will obtain. An attempt at a justification is discussed in appendix A.

Let us evaluate the resulting expression, setting $D^w_{m_i,k_i/\lambda ,m_j,k_j/\lambda } \to 1$ in (64), keeping λ arbitrary for now and keeping in mind that ultimately we will be interested in the limit λ → +∞. Using the expression for a determinant as a sum of permutations σ ∈ S_ns of signature (−1)^σ, ${\rm det} M = \sum _\sigma (-1)^\sigma \prod _{j=1}^{n_{\rm s}} M_{j,\sigma (j)}$, and the re-exponentiation formula 1/a = ∫ _v>0e^−av, we introduce n_s auxiliary variables v_j and rewrite as follows:

$$\begin{eqnarray} &&Z(n_{\rm s},s) = \sum _{\sigma } (-1)^\sigma \prod _{j=1}^{n_{\rm s}} \sum _{m_j=1}^{+\infty } 2^{m_j+1} \int _{v_j>0} \int \frac {{\rm d} k_j}{2 \pi } \,{\rm d} y_j\, \frac {(-1)^{m_j} \Gamma (({2 {\rm i} k_j + 2 \tilde w})/{\lambda })}{\Gamma (({2 {\rm i} k_j + 2 \tilde w})/{\lambda } + m_j)} \nonumber \\ &&\times \ {Ai}(y_j+ 4 k_j^2 + s) {\rm e} ^{\lambda m_j (y_j - {\rm i} k_j \tilde x) - 2 {\rm i} (k_j - k_{\sigma (j)}) v_j - v_j (m_j + m_{\sigma (j)})}. \label {3} \end{eqnarray} \tag{ 66 }$$

We can now use ∑ _jv_ja_σ(j) = ∑ _jv_σ⁻¹(j)a_j and relabel the sum over permutations as σ → σ⁻¹ to obtain

$$\begin{eqnarray} &&Z(n_{\rm s},s) = \sum _{\sigma } (-1)^\sigma \prod _{j=1}^{n_{\rm s}} \sum _{m_j=1}^{+\infty } 2^{m_j+1} \int _{v_j>0} \int \frac {{\rm d} k_j}{2 \pi }\, {\rm d} y_j \frac {(-1)^{m_j} \Gamma (({2 {\rm i} k_j + 2 \tilde w})/{\lambda })}{\Gamma (({2 {\rm i} k_j + 2 \tilde w})/{\lambda } + m_j)} \nonumber \\ &&\times \ {Ai}(y_j+ 4 k_j^2 + s) {\rm e} ^{\lambda m_j (y_j - {\rm i} k_j \tilde x) - 2 {\rm i} k_j (v_j - v_{\sigma (j)}) - m_j (v_j + v_{\sigma (j)})} \label {3} \end{eqnarray} \tag{ 67 }$$

where now we can further shift the variable $y \to y + v_j + v_{\sigma (j)} + {\rm i} k_j \tilde x$ using the identity (for λ > 0)

$$\begin{eqnarray} &&\int _{-\infty }^{+\infty } {\rm d} y\, {Ai}(y) {\rm e} ^{\lambda (y - {\rm i} k x)} = \int _{-\infty }^{+\infty } {\rm d} y\, {Ai}(y+ {\rm i} k x) {\rm e} ^{\lambda y}. \end{eqnarray} \tag{ 68 }$$

Under this form it clearly appears that Z(n_s, s) has a determinantal form:

$$\begin{eqnarray}&&Z(n_{\rm s},s) = \prod _{j=1}^{n_{\rm s}} \int _{v_j>0} {\rm det} M(v_i,v_j)|_{n_{\rm s} \times n_{\rm s}} \end{eqnarray} \tag{ 69 }$$

with the kernel

$$\begin{eqnarray} &&M(v_1,v_2) = \int \frac {{\rm d} k}{2 \pi }\, {\rm d} y \, {Ai}(y + 4 k^2 + {\rm i} k \tilde x + v_1 + v_2 + s) {\rm e} ^{-2 {\rm i} k (v_1-v_2)} \phi _\lambda (k,y) \label {M} \end{eqnarray} \tag{ 70 }$$

$$\begin{eqnarray} &&\phi _\lambda (k,y) = \sum _{m=1}^\infty \frac {(-1)^{m} 2^{m+1} \Gamma (({2 {\rm i} k + 2 \tilde w})/{\lambda })}{\Gamma (({2 {\rm i} k + 2 \tilde w})/{\lambda } + m)} {\rm e} ^{\lambda m y} \end{eqnarray} \tag{ 71 }$$

which we now study in the large λ limit. We show that

$$\begin{eqnarray} &&\label {lim1} \phi _{+\infty }(k,y) = - 2 \theta (y) - \frac {1}{{\rm i} k + \tilde w} \delta (y). \end{eqnarray} \tag{ 72 }$$

There are several ways to do that; the simplest is to use the Mellin–Barnes (MB) identity:

$$\begin{eqnarray} &&\label {MB} \sum _{m=1}^{+\infty } (-1)^{m} f(m) = \frac {-1}{2 {\rm i} } \int _{C} {\rm d} s\, \frac {1}{\sin \pi s} f(s) \end{eqnarray} \tag{ 73 }$$

where C_j = a + ir, 0 < a < 1, r ∈] −∞, ∞[. It requires being able to deform the contour and close it around the positive real axis, picking up the residues of the inverse sine function. Clearly the conditions for that are (i) f(s) has no pole for Re(s) ≥ a, (ii) f(s) does not grow too fast at large Re(s) > 0. The first condition is necessary for us not to 'miss' any pole: in fact if there are such poles in f(s) they can just be added to the formula. Here both conditions are clearly satisfied. Hence we obtain

$$\begin{eqnarray} &&\phi _\lambda (k,y) = \frac {-1}{2 {\rm i} } \int _{C} {\rm d} s\, \frac {1}{\sin \pi s} 2^{s+1} \frac {\Gamma (({2 {\rm i} k + 2 \tilde w})/{\lambda })}{\Gamma (({2 {\rm i} k + 2 \tilde w})/{\lambda } + s)} {\rm e} ^{\lambda s y} \end{eqnarray} \tag{ 74 }$$

and with the rescaling s_j → s_j/λ, we obtain, in the limit λ → +∞,

$$\begin{eqnarray} &&\phi _{+\infty }(k,y) = \int _{C} \frac {- {\rm d} s}{2 {\rm i} \pi s} \frac {2 {\rm i} k + 2 \tilde w + s}{{\rm i} k + \tilde w} {\rm e} ^{s y} \end{eqnarray} \tag{ 75 }$$

where now the contours C_j are the same as above, but with a = 0⁺. We used that Γ(x/λ) ∼ λ/x at large λ. We can now perform the integrations over the s_j, using

$$\begin{eqnarray} &&\int _{C} \frac {- {\rm d} s}{2 {\rm i} \pi s} {\rm e} ^{s y } = - \theta (y) , \quad\qquad \int _{C} \frac {- {\rm d} s}{2 {\rm i} \pi } {\rm e} ^{s y} = - \delta (y)\label {eq76} \end{eqnarray} \tag{ 76 }$$

and we obtain (72). Note that 'undoing' the MB trick, one sees that at large λ

$$\begin{eqnarray} &&\phi _\lambda (k,y) \simeq \sum _{m=1}^\infty (-1)^{m} \frac {2 {\rm i} k + 2 \tilde w + \lambda m}{{\rm i} k + \tilde w} {\rm e} ^{\lambda m y} \end{eqnarray} \tag{ 77 }$$

$$\begin{eqnarray} &&= \left (2 + \frac {1}{{\rm i} k + \tilde w} \partial _y\right ) \frac {{\rm e} ^{\lambda y}}{1+ {\rm e} ^{\lambda y}} \to _{\lambda \to +\infty } - 2 \theta (y) - \frac {1}{{\rm i} k + \tilde w} \delta (y) , \end{eqnarray} \tag{ 78 }$$

re-obtaining the same result via a direct summation over m.⁶

Inserting (72) into the kernel M we finally obtain the large λ limit:

$$\begin{eqnarray}&&Z(n_{\rm s},s) = \prod _{j=1}^{n_{\rm s}} (-1)^{n_{\rm s}} \int _{v_j>0} {\rm det} K(v_i,v_j)|_{n_{\rm s} \times n_{\rm s}}. \end{eqnarray} \tag{ 79 }$$

Hence the generating function takes the form of a Fredholm determinant:

$$\begin{eqnarray} &&\label {fd1} g_{\infty }(s) = {\rm Det}[I - {\cal K}] , \quad\qquad {\cal K}(v_1,v_2) = \theta (v_1) \theta (v_2) K(v_1,v_2) \end{eqnarray} \tag{ 80 }$$

with the kernel

$$\begin{eqnarray} &&\label {K0} K(v_1,v_2) = \int \frac {{\rm d} k}{2 \pi } \,{\rm d} y\, \left (2 \theta (y) + \frac {\delta (y) }{{\rm i} k + \tilde w} \right ) {Ai}(y + 4 k^2 + {\rm i} k \tilde x + v_1 + v_2 + s) {\rm e} ^{-2 {\rm i} k (v_1-v_2)} \end{eqnarray} \tag{ 81 }$$

which is our main result, with here $\tilde w>0$, and we recall that $\tilde x=x/\lambda ^2$ and $\tilde w=\lambda w$. The STS symmetry can be checked by performing the shift ${\rm i} k \to {\rm i} k + {\tilde x}/{8}$ and bringing the contour back to the real axis. This effects the shifts $w \to w + {\tilde x}/{8}$ and $s \to s + {\tilde x^2}/{16}$ in agreement with (65).⁷ Hence $\tilde g_{\infty }$ in that formula is also given by (80) and the kernel K, but with $\tilde x$ set to 0.

The GUE limit is easy to check on this form for K. Setting $\tilde x=0$ and $\tilde w \to + \infty$, the second part of K vanishes and one recovers exactly the GUE kernel in the form given in equation (26) of [16] (after the change k → k/2).

Checking the GOE limit is more delicate. One can take w = 0⁺ and let x →−∞. In that limit it turns out that one can make the replacement

$$\begin{eqnarray} &&\frac {1}{{\rm i} k + 0^+} \to 2 \pi \delta (k) \end{eqnarray} \tag{ 82 }$$

(a related property was noted in [20]), and that the first term vanishes. Hence K → B_s, the kernel of the F₁ distribution.

We now give an equivalent form of the kernel where the limits can be conveniently studied.

We now display three useful identities involving Airy functions. The first one is

$$\begin{eqnarray} &&\label {id1} 2 \int \frac {{\rm d} k}{2 \pi } {Ai}(4 k^2 + a+b+ {\rm i} k \tilde x) {\rm e} ^{2 {\rm i} k (b-a)}\nonumber \\ &&= 2^{-{1}/{3}} {Ai}\left (2^{{1}/{3}} \left (a+\frac {\tilde x^2}{32}\right )\right ) {Ai}\left (2^{{1}/{3}} \left (b+\frac {\tilde x^2}{32}\right )\right ) {\rm e} ^{({\tilde x}/{4}) (b-a)} \end{eqnarray} \tag{ 83 }$$

where $a,b,k,\tilde x$ are real numbers. This identity is well known in the case $\tilde x=0$  [48]. Starting from the identity for $\tilde x=0$, we can make the shifts ${\rm i} k \to {\rm i} k - {\tilde x}/{8}$ and $a \to a+{\tilde x^2}/{32}$, $b \to b+{\tilde x^2}/{32}$ to obtain the above identity, but now k is on a contour parallel to the real axis. Bringing this contour back to the real line, we obtain (83).

The second identity reads, for $\tilde w>0$,

$$\begin{eqnarray} &&2 \int \frac {{\rm d} k}{2 \pi } {Ai}(4 k^2 + a+b+ {\rm i} k \tilde x) \frac {{\rm e} ^{2 {\rm i} k (b-a)}}{{\rm i} k + \tilde w} = \int _0^{+\infty } {\rm d} r \, 2^{-{1}/{3}} {Ai}\left (2^{{1}/{3}} \left (a+\frac {r}{4}+\frac {\tilde x^2}{32}\right )\right )\nonumber \\ &&\times \ {Ai}\left (2^{{1}/{3}} \left (b-\frac {r}{4}+\frac {\tilde x^2}{32}\right )\right ) {\rm e} ^{({\tilde x}/{4}) (b-a)- r ({\tilde x}/{8}+\tilde w)}. \label {id2} \end{eqnarray} \tag{ 84 }$$

It is obtained by introducing an auxiliary variable, writing ${1}/({{\rm i} k + \tilde w}) = \int _0^{+\infty } {\rm d} r\, {\rm e} ^{- r({\rm i} k + \tilde w)}$, then using the above identity (83) with a → a + r/4, b → b − r/4.⁸

Note that if we set $\tilde w<0$ we can use instead ${1}/({{\rm i} k + \tilde w}) =- \int _{-\infty }^0 {\rm d} r\, {\rm e} ^{-r({\rm i} k + \tilde w)}$; hence we obtain exactly the same integral with $\int _0^{+\infty } {\rm d} r \to - \int _{-\infty }^0 {\rm d} r$. Here we do not need $\tilde w<0$; however it is useful to consider the limit $\tilde w=0^+$ minus $\tilde w=0^-$, which picks up the residue of the pole at k = 0 leading to another useful identity:

$$\begin{eqnarray} &&\label {id4} \int _{-\infty }^{+\infty } {\rm d} r \, 2^{-4/3} {Ai}\left (2^{{1}/{3}} \left (a+\frac {r}{4}+\frac {\tilde x^2}{32}\right )\right )\nonumber \\ &&\times \ {Ai}\left (2^{{1}/{3}} \left (b-\frac {r}{4}+\frac {\tilde x^2}{32}\right )\right ) {\rm e} ^{- r ({\tilde x}/{8})} = {Ai}(a+b) {\rm e} ^{({\tilde x}/{4}) (a-b)}. \end{eqnarray} \tag{ 85 }$$

Using (83) and (84) with a = v₁ + (y + s)/2, b = v₂ + (y + s)/2 we can rewrite the kernel (81) equivalently (see footnote 7) as

$$\begin{eqnarray} &&K(v_1,v_2) = \int _{0}^{+\infty } {\rm d} r \int \frac {{\rm d} k}{2 \pi } {\rm d} y \, \left (\theta (y) \delta (r) + \frac {1}{2} \delta (y) \right ) \end{eqnarray} \tag{ 86 }$$

$$\begin{eqnarray} &&\times \ 2^{-1/3} {Ai}\left (2^{{1}/{3}} \left (v_1 + \frac {y+s}{2} + \frac {r}{4} +\frac {\tilde x^2}{32} \right )\right ) \nonumber \\ &&\times \ {Ai}\left (2^{{1}/{3}} \left (v_2 + \frac {y+s}{2} - \frac {r}{4} +\frac {\tilde x^2}{32}\right ) \right ) {\rm e} ^{- r (\tilde w+{\tilde x}/{8})}. \end{eqnarray} \tag{ 87 }$$

We now carry out the rescaling y → 2^2/3y, r → 2^5/3r. Using the similarity transformation

$$\begin{eqnarray}&&K(v_1,v_2) = 2^{{1}/{3}} \tilde K(2^{{1}/{3}} v_1,2^{{1}/{3}} v_2) \end{eqnarray} \tag{ 88 }$$

and changing the notation: r → y in the second integral, we obtain the equivalent form for the kernel:

$$\begin{eqnarray} &&\label {result2} g_\infty (s) = {\rm Prob}(\xi < s) = {\rm Det}[I - {\cal K} ] , \quad\qquad {\cal K}(v_1,v_2) = \theta (v_1) \theta (v_2) \tilde K(v_1,v_2) \end{eqnarray} \tag{ 89 }$$

$$\begin{eqnarray} &&\tilde K(v_1,v_2) = K_{{Ai}}(v_1+\sigma ,v_2+\sigma ) + K^u_2(v_1+\sigma ,v_2+\sigma ) , \quad\qquad \sigma = 2^{-2/3} \left (s + \frac {\tilde x^2}{16}\right ) \end{eqnarray} \tag{ 90 }$$

in terms of the standard Airy kernel (14) and the kernel:

$$\begin{eqnarray} &&\label {result3} K^u_{2}(v_1,v_2) = \int _{y>0} {\rm d} y\, {Ai}(v_1 + y) {Ai}(v_2 - y) {\rm e} ^{ 2 y u} , \quad\qquad u = - 2^{2/3} \left (\tilde w + \frac {\tilde x}{8}\right )\nonumber \\ &&= {-} \int _{y<0} {\rm d} y\, {Ai}(v_1 + y) {Ai}(v_2 - y) {\rm e} ^{ 2 y u }\nonumber \\ &&\quad +\ 2^{-{1}/{3}} {Ai}(2^{-{1}/{3}} (v_1+v_2 - 2 u^2)) {\rm e} ^{- u(v_1-v_2)} \end{eqnarray} \tag{ 91 }$$

where we recall that $\tilde w= \lambda w$, $x = \lambda ^2 \tilde x$ and λ = (t/4)^1/3. The second form for K₂ is obtained by making the substitutions r → 2^5/3y, $a+{\tilde x^2}/{32} \to 2^{-1/3} v_1$, $b+{\tilde x^2}/{32} \to 2^{-1/3} v_2$ and ${\tilde x}/{8} \to - 2^{-2/3} u$ in (85).

It is easy to recover the GUE droplet limit by taking $\tilde w + {\tilde x}/{8} \to +\infty$ in (89)–(91). One sees that K₂ vanishes in that limit; hence one recovers

$$\begin{eqnarray} &&g_\infty (s) = {\rm Prob}(\xi < s) \to F_2\left (\sigma =2^{-2/3} \left (s + \frac {\tilde x^2}{16}\right ) \right ) \Leftrightarrow \lambda \xi = \chi _2 t^{1/3} - \frac {x^2}{4 t} \end{eqnarray} \tag{ 92 }$$

which coincides with the known result (15). Note that it is in fact a double limit, where we keep the combination $s+ {\tilde x^2}/{16}$ finite, to account for the average profile − x²/4t of the droplet solution.

To recover the GOE flat limit, we need to consider $\tilde w + {\tilde x}/{8} \to - \infty$ (while keeping $\tilde w>0$, a purely technical restriction). This time, since the average profile is flat we keep s finite. Hence K_Ai(v₁ + σ, v₂ + σ) vanishes in that limit, and so does the first term in the second expression for K₂. Hence we are left with only the second piece of K₂, or more precisely,

$$\begin{eqnarray} &&{\cal K}(v_1,v_2) \simeq _{\tilde {x} \to - \infty } 2^{-{1}/{3}} {Ai}(2^{-{1}/{3}} (v_1+v_2 + 2 \sigma - 2 u^2)) \theta (v_1) \theta (v_2) \end{eqnarray} \tag{ 93 }$$

where we have again discarded the factor e^{−τ(v₁−v₂)} which is immaterial in calculating the Fredholm determinant. Performing the change v₁ → 2^1/3v₁, v₂ → 2^1/3v₂ and comparing with (24), we obtain

$$\begin{eqnarray}&&g_\infty (s) = {\rm Prob}(\xi < s) \to F_1(s - 4 \tilde w^2 - \tilde w \tilde x) \Leftrightarrow \lambda \xi = \lambda \chi _1 + w x + t w ^2 \end{eqnarray} \tag{ 94 }$$

and hence we recover the GOE Tracy–Widom distribution, up to a shift equal to the average profile, i.e. the solution of the KPZ equation in the absence of noise with initial condition wx.

One can now compare (89)–(91) with the result of appendix A of [41]. The kernel there is identical to ours provided we make the identification

$$\begin{eqnarray}&&2^{-2/3} \xi = - 2^{-2/3} \frac {\tilde x^2}{16} + {\cal A}_{2 \to 1}(u) + \max (0,u)^2 , \quad\qquad u = - 2^{2/3} \left (\tilde w + \frac {\tilde x}{8}\right ) . \end{eqnarray} \tag{ 95 }$$

This can also be written as (ξ being defined in (24))

$$\begin{eqnarray} &&\lambda \xi = - \frac {x^2}{4 t} + t^{1/3} ({\cal A}_{2 \to 1}(u) - \min (0,u)^2 + u^2 ) \end{eqnarray} \tag{ 96 }$$

which is exactly (in rescaled variables, and for z = 0) the prediction of equation (38) obtained there from the argument of dominance of the maximum in the large time limit. Hence we recover quite precisely for the KPZ equation, from the RBA calculation, the transition process which was obtained in the context of the TASEP. This shows the desired universality.

11.1. Definitions and relations

It turns out that the Bethe ansatz formula (45) is easily generalized to study the partition sums of a DP where each of the two endpoints is free to explore its own half-space. This in turn gives interesting information on the extremal properties of the transition process ${\cal A}_{2 \to 1}$ (minus a half-parabola). There are clearly two cases: either the two half-spaces are on the same side, or they are on opposite sides; see figures 2 and 3. We thus now define

$$\begin{eqnarray} &&h^{\rm LL}_{zwz^{\prime }w^{\prime }}(t) : = \ln \int _{x<z^{\prime }} {\rm d} x \int _{y < z} {\rm d} y\, {\rm e} ^{h(x,t|y,0)+ w y + w^{\prime } x} = \ln \int _{x < z^{\prime }} {\rm d} x\, {\rm e} ^{h^L_{wz}(x,t) + w^{\prime } x} \end{eqnarray} \tag{ 97 }$$

$$\begin{eqnarray} &&h^{\rm LR}_{zwz^{\prime }w^{\prime }}(t) : = \ln \int _{x > z^{\prime }} {\rm d} x \int _{y < z} {\rm d} y\, {\rm e} ^{h(x,t|y,0)+ w y - w^{\prime } x} = \ln \int _{x > z^{\prime }} {\rm d} x\, {\rm e} ^{h^L_{wz}(x,t) - w^{\prime } x}. \end{eqnarray} \tag{ 98 }$$

Note that h^LR is well defined for w = w' = 0, since, as can be seen in figure 3, the line tension of the polymer (i.e. the diffusion kernel) makes all integrals convergent. On the other hand h^LL is finite only for w, w' > 0 since there is nothing to prevent the polymer being arbitrary far to the left; see figure 2.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Again we can expect that in the large t limit these integrals will be dominated by their maximum. One thus expects, setting w = w' = 0, that

$$\begin{eqnarray} &&h^{\rm LR}_{zz^{\prime }}(t) = \ln \int _{x > z^{\prime }} {\rm d} x\, {\rm e} ^{h^L_{z}(x,t)} \to _{t \to + \infty } \max _{x>z^{\prime }} h^L_z(x,t) \end{eqnarray} \tag{ 99 }$$

$$\begin{eqnarray} &&\simeq t^{1/3} \max _{x>z^{\prime }}[{\cal A}_{2 \to 1}(v) - \min (0,v)^2 ]_{v=(z-x)/(2 t^{2/3})} \end{eqnarray} \tag{ 100 }$$

$$\begin{eqnarray} &&= t^{1/3} \max _{v < u=({z-z^{\prime }})/{2 t^{2/3}}} [{\cal A}_{2 \to 1}(v) - \min (0,v)^2 ] \label {max5} \end{eqnarray} \tag{ 101 }$$

where in the second line we have used (34). Because of the term −min(0, v)², this optimization problem is well defined for v →−∞, the GUE side. Optimization on the complementary interval [u, +∞[(the GOE side) is clearly divergent.

Keeping now w, w' > 0 we can also write

$$\begin{eqnarray} &&h^{\rm LL}_{zwz^{\prime }w^{\prime }}(t) = \ln \int _{x < z^{\prime }} {\rm d} x\, {\rm e} ^{h^L_{z}(x,t) + w^{\prime } x} \to _{t \to + \infty } \max _{x<z^{\prime }} (h^L_{zw}(x,t) + w^{\prime } x) \end{eqnarray} \tag{ 102 }$$

$$\begin{eqnarray} &&\simeq t w^2 + \max _{x<z^{\prime }} ((w+w^{\prime }) x + t^{1/3}\nonumber \\ &&\quad \times \ [{\cal A}_{2 \to 1}(v) - \min (0,v)^2 ]_{v=- t^{1/3} w + ({z-x})/{2 t^{2/3}}}) \end{eqnarray} \tag{ 103 }$$

$$\begin{eqnarray} &&= - t w^2 - 2 t w w^{\prime } + (w+w^{\prime }) z \nonumber \\ &&\quad +\ t^{1/3} \max _{v> u= ({z-z^{\prime }-2 t w})/{2 t^{2/3}}} [{\cal A}_{2 \to 1}(v) - \min (0,v)^2 - 2 v \times 2^{2/3} (\tilde w+\tilde w^{\prime }) ] \label {maxAiry21new} \end{eqnarray} \tag{ 104 }$$

where in the second line we have used (38) and we require w + w' > 0 for the problem to be well defined. We have defined the scaled variables $\tilde w= \lambda w$ and $\tilde w^{\prime }=\lambda w^{\prime }$; hence $2^{2/3} (\tilde w+\tilde w^{\prime })=t^{1/3} (w+w^{\prime })$. Note the symmetry property which arises from the above definitions: $h^{\rm LL}_{zwz^{\prime }w^{\prime }}(t) \equiv h^{\rm LL}_{z^{\prime }w^{\prime }zw}(t)$ which implies $\max _{x<z} (h^L_{z^{\prime }w^{\prime }}(x,t) + w x) \equiv \max _{x<z^{\prime }} (h^L_{zw}(x,t)+ w^{\prime } x)$, and hence (104) must also be symmetric w.r.t. to the exchange of (z, w) with (z', w'). This can be checked in the absence of noise where the solution, in the infinite time limit, reads (this amounts to setting ${\cal A}_{2 \to 1}(v) \to 0$ in (104))

$$\begin{eqnarray} &&h^{LL0}_{zwz^{\prime }w^{\prime }}(t) = \max _{x<z^{\prime }, y<z} \left (- \frac {(x-y)^2}{4 t} + w y + w^{\prime } x\right ) = \theta (z^{\prime }-z>2 w^{\prime } t) [t w^{\prime 2} + (w+w^{\prime }) z ] \nonumber \\ &&+\ \theta (2 w t< z^{\prime }-z<2 w^{\prime } t) \left [w z + w^{\prime } z^{\prime } - \frac {(z-z^{\prime })^2}{4 t}\right ]\nonumber \\ &&+\ \theta (z^{\prime }-z<-2 w t) [t w^2 + (w+w^{\prime }) z^{\prime } ] \end{eqnarray} \tag{ 105 }$$

which is complicated but clearly symmetric in the exchange of (z, w) with (z', w'). The fact that such a symmetry holds also (in law) for the noisy case is not entirely easy to guess from just looking at (104). However it must be correct, and we do indeed find that our result below satisfies it.

11.2. Quantum mechanics

Let us now express the moments of the partition sums:

$$\begin{eqnarray}&&Z^{\rm LL}(t) = Z^{\rm LL}_{zwz^{\prime }w^{\prime }}(t) = {\rm e} ^{h^{\rm LL}_{zwz^{\prime }w^{\prime }}(t)} \end{eqnarray} \tag{ 106 }$$

$$\begin{eqnarray}&&Z^{\rm LR}(t) = Z^{\rm LR}_{zwz^{\prime }w^{\prime }}(t) = {\rm e} ^{h^{\rm LR}_{zwz^{\prime }w^{\prime }}(t)} \end{eqnarray} \tag{ 107 }$$

using the eigenstates μ = {λ₁, ..., λ_n} of the Lieb–Liniger model. Generalizing formula (45) we see that

$$\begin{eqnarray} &&\overline {(Z^{\rm LL})^n} = \sum _\mu (I_\mu ^L(w^{\prime }) )^* {\rm e} ^{ (n w^{\prime }- {\rm i} \sum _\alpha \lambda ^*_\alpha ) z^{\prime }} \frac {{\rm e} ^{-t E_\mu } }{\Vert \mu \Vert ^2} {\rm e} ^{ (n w+{\rm i} \sum _\alpha \lambda _\alpha ) z} I_\mu ^L(w) \end{eqnarray} \tag{ 108 }$$

$$\begin{eqnarray} &&\overline {(Z^{\rm LR})^n} = \sum _\mu (I_\mu ^R(w^{\prime }) )^* {\rm e} ^{ (- n w^{\prime }- {\rm i} \sum _\alpha \lambda ^*_\alpha ) z^{\prime }} \frac {{\rm e} ^{-t E_\mu } }{\Vert \mu \Vert ^2} {\rm e} ^{ (n w+{\rm i} \sum _\alpha \lambda _\alpha ) z} I_\mu ^L(w) \end{eqnarray} \tag{ 109 }$$

where we have defined

$$\begin{eqnarray}&&I_\mu ^L(w) = \prod _{j=1}^n \int _{-\infty }^0 {\rm d} y_j\, {\rm e} ^{w y_j} \Psi _\mu (y_1\cdots y_n) \end{eqnarray} \tag{ 110 }$$

$$\begin{eqnarray}&&I_\mu ^R(w^{\prime }) = \prod _{j=1}^n \int ^{+\infty }_{0} {\rm d} x_j\, {\rm e} ^{- w^{\prime } x_j} \Psi _\mu (x_1 \cdots x_n) = I_{-\mu }^L(w^{\prime }) \end{eqnarray} \tag{ 111 }$$

where − μ denotes the state with reversed rapidities − μ = {− λ₁, ..., −λ_n} and we use Ψ_μ(−x₁, ..., −x_n) = Ψ_−μ(x₁, ..., x_n), as can be seen from (46).

Up to now the formulas have been general. Let us now consider the limit L → +∞ and insert the string states. Let us define

$$\begin{eqnarray} &&\label {shift} \ln Z^{\rm LL} = w z + w^{\prime } z^{\prime } + \ln \tilde Z^{\rm LL} , \quad\qquad \ln Z^{\rm LR} = w z - w^{\prime } z^{\prime } + \ln \tilde Z^{\rm LR}. \end{eqnarray} \tag{ 112 }$$

From the results of [19, 20] (equation (76)), and section 6 (see the notation there) we have

$$\begin{eqnarray}&&I_\mu ^L(w) = n! (-2)^n S^w[k,m] D^w[k,m] \end{eqnarray} \tag{ 113 }$$

$$\begin{eqnarray}&&I_\mu ^R(w^{\prime }) = n! (-2)^n S^{w^{\prime }}[-k,m] D^{w^{\prime }}[- k,m] = I_\mu ^L(w^{\prime })^* \end{eqnarray} \tag{ 114 }$$

and we recall the property

$$\begin{eqnarray}&&(S^w_{m,k})^* = S^w_{m,- k} , \quad\qquad (D^w_{m_1,k_1,m_2,k_2})^*=D^w_{m_1,-k_1,m_2,-k_2} \end{eqnarray} \tag{ 115 }$$

from the definitions (55), (56).

The moments thus read

$$\begin{eqnarray} &&\overline {(\tilde Z^{\epsilon })^n} = \sum _{n_{\rm s}=1}^n \frac {n! (-4)^n}{n_{\rm s}!} \sum _{(m_1,\ldots ,m_{n_{\rm s}})_n} \Phi [k,m] S^w[k,m] S^{w^{\prime }}[\epsilon k,m] D^w[k,m] D^{w^{\prime }}[\epsilon k,m] \end{eqnarray} \tag{ 116 }$$

$$\begin{eqnarray} &&\times \ \prod _{j=1}^{n_{\rm s}} \frac {1}{m_j} {\rm e} ^{m_j^3 ({t}/{12})- m_j k_j^2 t - {\rm i} (z^{\prime }-z) m_j k_j} \end{eqnarray} \tag{ 117 }$$

where from now on we define

$$\begin{eqnarray}&&LL\quad \Leftrightarrow \quad \epsilon = -1, \quad\qquad LR\quad \Leftrightarrow \quad \epsilon = +1. \end{eqnarray} \tag{ 118 }$$

We then define the generating functions:

$$\begin{eqnarray}&&g_\lambda ^{\rm LL}(s) = \sum _{n=0}^{+\infty } \frac {1}{n!} {\rm e} ^{- \lambda n s} \overline {(\tilde Z^{\rm LL})^n} \end{eqnarray} \tag{ 119 }$$

and similarly for $g_\lambda ^{\rm LR}(s)$. It is easy to see that $g_\lambda ^{\epsilon }(s)$ is then given exactly by the same formula as g_λ(s) in (54) with the substitution [47]

$$\begin{eqnarray}&&S^w_{m_j,k_j} \to (-2)^{m_j} S^w_{m_j,k_j} S^{w^{\prime }}_{m_j, \epsilon k_j} , \quad\qquad x \to z^{\prime }-z \end{eqnarray} \tag{ 120 }$$

$$\begin{eqnarray}&&D^w_{m_i,k_i,m_j,k_j} \to D^w_{m_i,k_i,m_j,k_j} D^{w^{\prime }}_{m_i, \epsilon k_i,m_j, \epsilon k_j}. \end{eqnarray} \tag{ 121 }$$

11.3. The large time limit and the first form for the kernel

We now consider the large time limit and again set all factors D^w, D^w' to unity. We define again the scaled variables $\tilde z=z/\lambda ^2$, $\tilde z^{\prime }=z^{\prime }/\lambda ^2$, $\tilde w= \lambda w$, $\tilde w^{\prime }= \lambda w^{\prime }$. Performing exactly the same steps as in sections 7 and 8, and using the formula (55), we arrive at the following expressions in terms of Fredholm determinants:

$$\begin{eqnarray}&&g_\lambda ^{\epsilon }(s) \to {\rm Det}[I - {\cal M}] , \quad\qquad {\cal M}(v_1,v_2) = \theta (v_1) \theta (v_2) M(v_1,v_2) \end{eqnarray} \tag{ 122 }$$

with the same kernel M as in (70) (with $\tilde x=\tilde z-\tilde z^{\prime }$) with

$$\begin{eqnarray} &&\phi _\lambda (k,y) \to \phi ^{\epsilon }_\lambda (k,y) = \sum _{m=1}^\infty \frac {(-1)^{m} 2^{2m+1} \Gamma (({2 {\rm i} k + 2 \tilde w})/{\lambda }) \Gamma (({2 {\rm i} k \epsilon + 2 \tilde w^{\prime }})/{\lambda })} {\Gamma (({2 {\rm i} k + 2 \tilde w})/{\lambda } + m) \Gamma (({2 {\rm i} k \epsilon + 2 \tilde w^{\prime }})/{\lambda } + m)} {\rm e} ^{\lambda m y}. \end{eqnarray} \tag{ 123 }$$

We again use the Mellin–Barnes identity (73) and carry out the rescaling s_j → s_j/λ, to obtain, in the limit λ → +∞,

$$\begin{eqnarray} &&\phi ^{\epsilon }_{+\infty }(k,y) = \int _{C} \frac {- {\rm d} s}{2 {\rm i} \pi s} \frac {1}{2} \frac {(2 {\rm i} k + 2 \tilde w + s)(2 {\rm i} k \epsilon + 2 \tilde w^{\prime } + s)}{({\rm i} k + \tilde w)({\rm i} k \epsilon + \tilde w^{\prime })} {\rm e} ^{s y} \end{eqnarray} \tag{ 124 }$$

$$\begin{eqnarray} &&= \int _{C} \frac {- {\rm d} s}{2 {\rm i} \pi s} \left [2 + \frac {s}{{\rm i} k + \tilde w} + \frac {s}{ {\rm i} k \epsilon + \tilde w^{\prime }} + \frac {1}{2} \frac {s^2}{({\rm i} k + \tilde w) ({\rm i} k \epsilon + \tilde w^{\prime })} \right ] {\rm e} ^{s y} \end{eqnarray} \tag{ 125 }$$

$$\begin{eqnarray} &&= {-} 2 \theta (y) - \left [\frac {1}{{\rm i} k + \tilde w} + \frac {1}{{\rm i} k \epsilon + \tilde w^{\prime }} \right ] \delta (y) - \frac {1}{2} \frac {1}{({\rm i} k + \tilde w)({\rm i} k \epsilon + \tilde w^{\prime })} \delta ^{\prime }(y). \end{eqnarray} \tag{ 126 }$$

Hence we finally obtain that

$$\begin{eqnarray} &&\label {defxi2} h^\epsilon _{zwz^{\prime }w^{\prime }}(t) = v_0 t + w x - \epsilon w^{\prime } x^{\prime } + \lambda \xi , \quad\qquad \lambda = (t/4)^{1/3} \end{eqnarray} \tag{ 127 }$$

with, as t →∞,

$$\begin{eqnarray} &&\label {fd2} {\rm Prob}(\xi < s) = g_\infty ^{\epsilon }(s) = {\rm Det}[I - {\cal K}^{\epsilon } ] , \quad\qquad {\cal K}^{\epsilon }(v_1,v_2) = \theta (v_1) \theta (v_2) K^{\epsilon }(v_1,v_2) \end{eqnarray} \tag{ 128 }$$

with the kernels

$$\begin{eqnarray} &&\label {KLL} K^{\epsilon }(v_1,v_2) = \int \frac {{\rm d} k}{2 \pi } \,{\rm d} y\, \Bigg [2 \theta (y) + \Bigg (\frac {1}{{\rm i} k + \tilde w} + \frac {1}{{\rm i} k \epsilon + \tilde w^{\prime }} \Bigg ) \delta (y) - \frac {1}{2} \frac {1}{({\rm i} k + \tilde w)({\rm i} k \epsilon + \tilde w^{\prime })} \delta (y) \partial _y \Bigg ] \nonumber \\ &&\times \ {Ai}(y + 4 k^2 + {\rm i} k (\tilde z^{\prime } - \tilde z ) + v_1 + v_2 + s) {\rm e} ^{-2 {\rm i} k (v_1-v_2)} \end{eqnarray} \tag{ 129 }$$

where $\tilde w, \tilde w^{\prime }>0$ and we recall that = −1 for LL and = +1 for LR. The STS symmetry is again recovered from the shift ${\rm i} k \to {\rm i} k + ({\tilde z^{\prime }-\tilde z})/{8}$ followed by the shift back to the real axis, and it shows that all the dependence in z, z', w, w' has the form (see footnote 7)

$$\begin{eqnarray} &&\label {sym1} g_\infty ^\epsilon (s) = \tilde g^\epsilon _\infty \left (s + \frac {(\tilde z^{\prime }-\tilde z)^2}{16} , \tilde w + \frac {\tilde z^{\prime }-\tilde z}{8} , \tilde w^{\prime } + \epsilon \frac {\tilde z^{\prime }-\tilde z}{8}\right ) \end{eqnarray} \tag{ 130 }$$

which is a symmetric function of its last two arguments (obvious for = +1 (LR) and using k →−k followed by the transposition of the kernel for = −1 (LL)). The function $\tilde g^\epsilon _\infty$ has the same form (128) with the same kernel K where $\tilde z - \tilde z^{\prime }$ is set to 0.

One easily checks some limits. Taking both $\tilde w, \tilde w^{\prime } \to + \infty$ in (129), one recovers the GUE kernel. The same is thus true if one takes $\tilde z^{\prime }-\tilde z \to + \infty$. If one takes $\tilde w^{\prime } \to + \infty$ at fixed w, one recovers the half-flat kernel (89)–(91) as expected.

11.4. The second form for the kernel

We again transform these kernels to another equivalent form. Details are given in appendix B. Our final result is that (127) holds with

$$\begin{eqnarray} &&\label {result5} g^\epsilon _\infty (s) = {\rm Prob}(\xi < s) = {\rm Det}[I - {\cal K}^\epsilon ] , \quad\qquad {\cal K}^\epsilon (v_1,v_2) = \theta (v_1) \theta (v_2) \tilde K^\epsilon (v_1,v_2) \end{eqnarray} \tag{ 131 }$$

with = −1 for LL, = +1 for LR and the kernel (see footnote 7)

$$\begin{equation*} \tilde K^{\epsilon }(v_1,v_2) = K_{{Ai}}(v_1+\sigma ,v_2+ \sigma ) + \bar K^{\epsilon }(v_1+\sigma ,v_2+\sigma ) , \quad\qquad \sigma = 2^{-2/3} \left (s + \frac {(\tilde z^{\prime }-\tilde z)^2}{16}\right ) \end{equation*}$$

where K_Ai is the Airy kernel (14) and

$$\begin{eqnarray} &&\bar K^{\rm LL}(v_1,v_2) = K_2^u(v_1,v_2) + K_2^{u^{\prime }}(v_2,v_1) + K_3^{\rm LL}(v_1,v_2)\label {result6} \end{eqnarray} \tag{ 132 }$$

$$\begin{eqnarray} &&\bar K^{\rm LR}(v_1,v_2) = K_2^u(v_1,v_2) + K_2^{u^{\prime }}(v_1,v_2) + K_3^{\rm LR}(v_1,v_2) \end{eqnarray} \tag{ 133 }$$

$$\begin{eqnarray}&&u = - 2^{2/3} \left (\tilde w + \frac {{\tilde z}^{\prime }-\tilde z}{8}\right ) , \quad\qquad u^{\prime } = - 2^{2/3} \left (\tilde w^{\prime } + \epsilon \frac {{\tilde z}^{\prime }-\tilde z}{8}\right ) \end{eqnarray} \tag{ 134 }$$

in terms of the kernel $K_2^u$ defined in (91) and in terms of a third kernel:

$$\begin{eqnarray} &&K_3^{\rm LL}(v_1,v_2) = (\partial _{v_1}+\partial _{v_2}) \int _0^{+\infty } {\rm d} r\, \frac {{Ai}(v_1+r){Ai}(v_2-r) {\rm e} ^{2 r u} + {Ai}(v_1-r){Ai}(v_2+r) {\rm e} ^{2 r u^{\prime }}}{2(u+u^{\prime })} \nonumber \\ &&K_3^{\rm LR}(v_1,v_2) = (\partial _{v_1}+\partial _{v_2}) \int _0^{+\infty } {\rm d} r\, {Ai}(v_1+r){Ai}(v_2-r) \frac {{\rm e} ^{2 r u} - {\rm e} ^{2 r u^{\prime }}}{2(u^{\prime }-u)}. \nonumber \\ &&\label {last} \end{eqnarray} \tag{ 135 }$$

We note that $\tilde K^{\rm LR}$ is invariant in the exchange of u and u', while $\tilde K^{\rm LL}$ is changed in its transpose⁹; hence we recover the symmetry of the function $\tilde g^\epsilon _{\infty }$ in equation (130).

11.5. The maximum of the transition process

As one example of an application, consider g^LR(s) and set w = w' = 0 and hence u = u'. Putting (101) together with our above result (131)–(135) and the definition of ξ (127), we obtain that

$$\begin{eqnarray}&&t^{1/3} \max _{v < u} [{\cal A}_{2 \to 1}(v) - \min (0,v)^2 ] = t^{1/3} \chi ^u - \frac {(z-z^{\prime })^2}{4 t} = t^{1/3} (\chi ^u - u^2) \end{eqnarray} \tag{ 136 }$$

where χ^u is distributed according to

$$\begin{eqnarray} &&{\rm Prob}(\chi ^u < S) = {\rm Det}[I - {\cal P}], \quad\qquad {\cal P}(v_1,v_2) = \theta (v_1) \theta (v_2) P(v_1+S,v_2+S) \end{eqnarray} \tag{ 137 }$$

$$\begin{eqnarray} &&P(v_1,v_2) = K_{{Ai}}(v_1,v_2) + (2 - \tfrac {1}{2} (\partial _{v_1} + \partial _{v_2}) \partial _u ) K_2^u(v_1,v_2) . \end{eqnarray} \tag{ 138 }$$

More results concerning the maximum of ${\cal A}_{2 \to 1}(v) - \min (0,v)^2 - b v$ on either the interval v ∈ [u, +∞[(RR) or the interval v ∈] −∞, u] are also easily extracted from the above formula (in view of e.g. (104)).

To conclude, we have shown how the replica Bethe ansatz allows us to find the large time limit of the PDF of the height field of the continuum KPZ equation for the half-flat initial condition. This PDF takes the form of a Fredholm determinant. We show that its kernel can be transformed to the one found for the TASEP with the corresponding initial condition, a manifestation of KPZ universality. Being confident that the procedure for taking the large time limit gives the correct answer, although this is at this stage not fully justifiable, we obtain the one-point PDF for the problem of a directed polymer with each endpoint on its own half-space. It also takes the form of Fredholm determinants with new kernels that we display and analyze. These are related to the extremal statistics of the half-flat initial condition. It seems that it should now be possible, by taking a similar limit, to study the many-point problem and recover the complete Airy_2→1 process.

It would also be interesting to test the present results numerically, or in liquid crystal experiments. They also have consequences for the conductance g of disordered 2D conductors deep in the Anderson localized regime, and specifically for the conductance from a point lead (x, t) to an extended lead (0, y)y ∈ [0, L[. Extending the results of [49], we surmise that the one-point distribution of lng, scaled by t^1/3, should exhibit the GUE to GOE universal crossover distribution. Similarly our LR (and LL) results can in principle be tested for two parallel half-line leads (eventually tilted by small angles of ∼w, w'). This could provide a rather detailed test of the conjectured relation between the positive weight DP problem and the Anderson problem, which, at present, is not based on any exactly solvable model.

I am grateful to J Quastel for suggesting the first part of this calculation, and informing me of work in preparation on flat and half-flat initial conditions [22]. I thank P Calabrese for discussions and collaborations closely related to many aspects of this work. I thank A Borodin for useful discussions.

The rationale for setting the D^w factor to unity in the large time limit is as follows. Assume that one can use the Mellin–Barnes identity (73) on the starting formula (64) and write

$$\begin{eqnarray} &&Z(n_{\rm s},s) = \prod _{j=1}^{n_{\rm s}} \int _{C_j} \frac {- {\rm d} s_j}{2 {\rm i} \pi \sin \pi s_j} 2^{s_j+1} \int \frac {{\rm d} k_j}{2 \pi } \int {\rm d} y_j {Ai}(y_j + 4 k_j^2 + {\rm i} k_j \tilde x + s)\nonumber \\ &&\times \ \frac { \Gamma (({2 {\rm i} k_j + 2 \tilde w})/{\lambda }) {\rm e} ^{\lambda s_j y}}{\Gamma (({2 {\rm i} k_j + 2 \tilde w})/{\lambda } + s_j)} \nonumber \\ &&\times \ \prod _{1 \leq {\rm i} < j \leq n_{\rm s}} D^w_{s_i,k_i/\lambda ,s_j,k_j/\lambda } \times {\rm det}\left [\frac {1}{ 2 {\rm i} (k_i - k_j) + \lambda s_i + \lambda s_j }\right ]_{n_{\rm s} \times n_{\rm s}} \label {new} \end{eqnarray} \tag{ A.1 }$$

where C_j = a + ir_j, 0 < a < 1. Then carrying out the rescaling s_j → s_j/λ and taking the large λ limit, one finds that we do indeed have $D^w_{s_i,k_i/\lambda ,s_j,k_j/\lambda } \to 1$ from the definition (56). Pursuing the calculation then immediately leads to the same formula as in section 8, as the s_j integrals then decouple.

This is the type of argument which was used in [28, 31, 33, 34]. At present its proper justification escapes us, however. One condition for the Mellin–Barnes identity (73) to hold is that f(s_j) has no poles for Res_j > a. One easily sees that the determinant is not a problem, as its poles for s_i + s_j live on the imaginary axis. However examination of the formula (56) for $D^w_{s_i,k_i/\lambda ,s_j,k_j/\lambda }$ (if we take it as the proper analytical continuation for complex m_j) shows that at fixed k_j it has numerous poles where some of the Res_j > a.

Given that we know that setting D^w → 1 does give the correct answer in a number of cases, including in the present study, it is quite likely that there is indeed an integral representation either identical or similar to the one given above. One way to check would be to actually enumerate the additional poles, add their contributions and show that they do indeed vanish for infinite λ. Another check would be to see whether the finite time solution of [19, 20] can also be retrieved from (A.1) or a modification thereof. Finally, analytical continuations in the m_j other than (56) may be searched for. These go beyond the present study. It is likely that a better understanding of why and how this limit works will come from the other routes, as limits from the ASEP, q-TASEP or the O'Connell semi-discrete polymer, which produce better controlled nested contour integral formulas (see e.g. [23, 22]).

Let us start with the kernel in (129). Writing in the last term ${1}/{({\rm i} k + \tilde w)({\rm i} k \epsilon + \tilde w^{\prime })} = {1}/({\tilde w^{\prime }-\epsilon \tilde w}) ({1}/({{\rm i} k + \tilde w}) - {\epsilon }/({{\rm i} k \epsilon + \tilde w^{\prime }}))$ using (84) with a = v₁ + (y + s/2), b = v₂ + (y + s/2) and carrying out the rescaling y → 2^2/3y, r → 2^5/3r, we find

$$\begin{eqnarray}&&K^\epsilon (v_1,v_2) = 2^{1/3} \tilde K^\epsilon (2^{1/3} v_1,2^{1/3} v_2). \end{eqnarray} \tag{ B.1 }$$

Hence we obtain equations (131) and (132) in the text with

$$\begin{eqnarray} &&\bar K^{\epsilon }(v_1,v_2) = \int _{0}^{+\infty } {\rm d} r \int \frac {{\rm d} k}{2 \pi } \,{\rm d} y\, \delta (y) \left (1- \frac {1}{2\times 2^{2/3} (\tilde w^{\prime } - \epsilon \tilde w)} \partial _y\right ) \end{eqnarray} \tag{ B.2 }$$

$$\begin{eqnarray} &&\times \ {Ai}\big (v_1 + y + r \big ) {Ai}\big (v_2 + y - r \big ) {\rm e} ^{- 2 r 2^{2/3} (\tilde w+({\tilde z^{\prime }-\tilde z})/{8})} \end{eqnarray} \tag{ B.3 }$$

$$\begin{eqnarray} &&+\ \int _{0}^{+\infty } {\rm d} r \int \frac {{\rm d} k}{2 \pi }\,{\rm d} y\, \delta (y) \left (1+ \frac {\epsilon }{2\times 2^{2/3} (\tilde w^{\prime } - \epsilon \tilde w)} \partial _y\right ) \end{eqnarray} \tag{ B.4 }$$

$$\begin{eqnarray} &&\times \ {Ai}\big (v_1 + y + \epsilon r \big ) {Ai}\big (v_2 + y - \epsilon r \big ) {\rm e} ^{- 2 r 2^{2/3} (\tilde w^{\prime }+ \epsilon ({\tilde z^{\prime }-\tilde z})/{8})}. \end{eqnarray} \tag{ B.5 }$$

This then leads to the form given in the text.