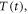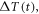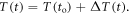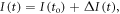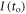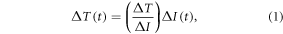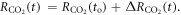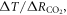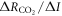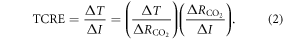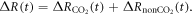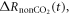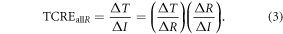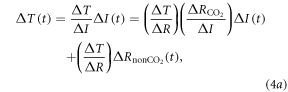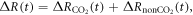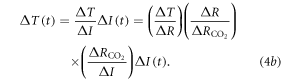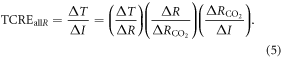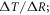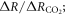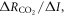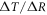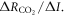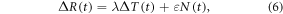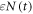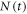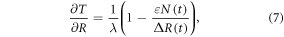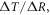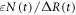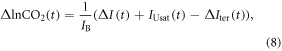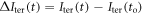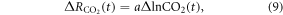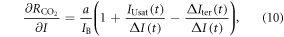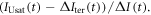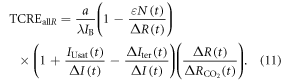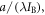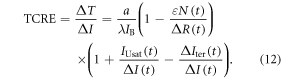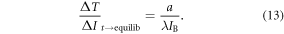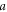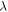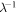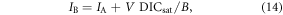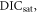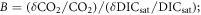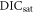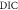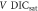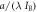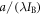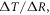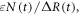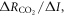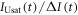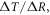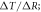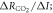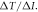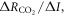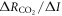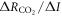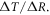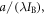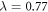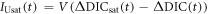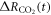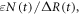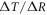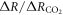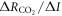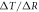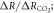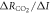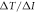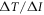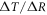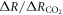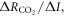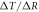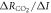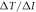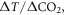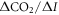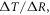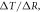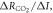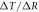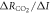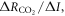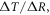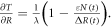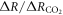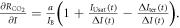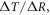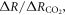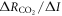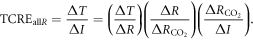A framework to understand the transient climate response to emissions

In order to understand our framework, assume that the global-mean surface air temperature (K) at time t, $T(t),$ is defined by a time-dependent anomaly, ${\rm{\Delta }}T(t),$ relative to the temperature at the pre-industrial at time t_o, $T(t)=T({t}_{{\rm{o}}})+{\rm{\Delta }}T(t).$ The cumulative amount of carbon (PgC) emitted to the atmosphere from all anthropogenic sources at time t is similarly defined, $I(t)=I({t}_{{\rm{o}}})+{\rm{\Delta }}I(t),$ with $I({t}_{{\rm{o}}})$ taken to be zero. The surface temperature anomaly is then related to the cumulative amount of carbon emitted since the pre-industrial via the transient climate response to cumulative carbon emissions, the TCRE, represented mathematically by ${\rm{\Delta }}T/{\rm{\Delta }}I$,

$$\begin{eqnarray}&&{\rm{\Delta }}T(t)=\left(\displaystyle \frac{{\rm{\Delta }}T}{{\rm{\Delta }}I}\right){\rm{\Delta }}I(t),\end{eqnarray} \tag{ 1 }$$

where the Δ notation denotes differences relative to the pre-industrial (rather than a small incremental interval). Our aim is now to connect this surface warming definition (1) to the controlling factors for the TCRE, which are assumed to be the dependence of surface warming on radiative forcing and the dependence of radiative forcing on cumulative carbon emissions.

Start by assuming that the radiative forcing (W m⁻²) driving climate change is only from atmospheric CO₂, which is defined by ${R}_{{{\rm{CO}}}_{2}}(t)\quad ={R}_{{{\rm{CO}}}_{2}}({t}_{{\rm{o}}})+{\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}(t).$ Here we choose to express the TCRE in (1) in terms of the product of the dependence of surface warming on radiative forcing from atmospheric CO₂, ${\rm{\Delta }}T/{\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}},$ and the dependence of radiative forcing on carbon emissions, ${\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}/{\rm{\Delta }}I$:

$$\begin{eqnarray}&&{\rm{TCRE}}=\displaystyle \frac{{\rm{\Delta }}T}{{\rm{\Delta }}I}=\left(\displaystyle \frac{{\rm{\Delta }}T}{{\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}}\right)\left(\displaystyle \frac{{\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}}{{\rm{\Delta }}I}\right).\end{eqnarray} \tag{ 2 }$$

More generally, the radiative forcing driving climate change includes contributions from atmospheric CO₂ and other non-CO₂ contributions, so that the change in radiative forcing since the pre-industrial era is given by ${\rm{\Delta }}R(t)={\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}(t)+{\rm{\Delta }}{R}_{{{\rm{nonCO}}}_{2}}(t).$ The change in non-CO₂ radiative forcing, ${\rm{\Delta }}{R}_{{{\rm{nonCO}}}_{2}}(t),$ includes contributions from aerosols emitted via anthropogenic and volcanic activity (Ottera et al 2010, Booth et al 2012) and other non-CO₂ greenhouse gases, such as methane with a shorter lifetime than CO₂ (Pierrehumbert 2014).

The definition of the TCRE may be extended to include the effect of all contributions to the radiative forcing, such that

$$\begin{eqnarray}&&{{\rm{TCRE}}}_{{\rm{all}}R}=\displaystyle \frac{{\rm{\Delta }}T}{{\rm{\Delta }}I}=\left(\displaystyle \frac{{\rm{\Delta }}T}{{\rm{\Delta }}R}\right)\left(\displaystyle \frac{{\rm{\Delta }}R}{{\rm{\Delta }}I}\right).\end{eqnarray} \tag{ 3 }$$

While this definition looses the clarity of the original TCRE definition in (2) in terms of isolating the climate response to cumulative carbon emissions, this generalisation for TCRE_{all R} in (3) is needed if the climate response is to be diagnosed from a climate model including non-CO₂ radiative forcing. To extend the TCRE definition in (3), the surface temperature change in (1) is written as

$$\begin{eqnarray}&&{\rm{\Delta }}T(t)=\displaystyle \frac{{\rm{\Delta }}T}{{\rm{\Delta }}I}{\rm{\Delta }}I(t)=\left(\displaystyle \frac{{\rm{\Delta }}T}{{\rm{\Delta }}R}\right)\left(\displaystyle \frac{{\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}}{{\rm{\Delta }}I}\right){\rm{\Delta }}I(t)\\ &&\quad \quad \quad \quad \;+\left(\displaystyle \frac{{\rm{\Delta }}T}{{\rm{\Delta }}R}\right){\rm{\Delta }}{R}_{{{\rm{nonCO}}}_{2}}(t),\end{eqnarray} \tag{ 4a }$$

which makes explicit the surface warming from the separate effects of the radiative forcing from CO₂ and non-CO₂ contributions. Exploiting the definition of ${\rm{\Delta }}R(t)={\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}(t)+{\rm{\Delta }}{R}_{{{\rm{nonCO}}}_{2}}(t),$ the surface warming is then equivalently written as

$$\begin{eqnarray}&&{\rm{\Delta }}T(t)=\displaystyle \frac{{\rm{\Delta }}T}{{\rm{\Delta }}I}{\rm{\Delta }}I(t)=\left(\displaystyle \frac{{\rm{\Delta }}T}{{\rm{\Delta }}R}\right)\left(\displaystyle \frac{{\rm{\Delta }}R}{{\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}}\right)\\ &&\quad \quad \quad \quad \;\times \left(\displaystyle \frac{{\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}}{{\rm{\Delta }}I}\right){\rm{\Delta }}I(t).\end{eqnarray} \tag{ 4b }$$

Accordingly, the definition for the TCRE for all radiative forcing contributions in (3) is then expressed as

$$\begin{eqnarray}&&{{\rm{TCRE}}}_{{\rm{all}}R}=\displaystyle \frac{{\rm{\Delta }}T}{{\rm{\Delta }}I}=\left(\displaystyle \frac{{\rm{\Delta }}T}{{\rm{\Delta }}R}\right)\left(\displaystyle \frac{{\rm{\Delta }}R}{{\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}}\right)\left(\displaystyle \frac{{\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}}{{\rm{\Delta }}I}\right).\end{eqnarray} \tag{ 5 }$$

This definition of the TCRE for all radiative forcing contributions in (5) is made up of the product of three differential terms: the dependence of surface warming on radiative forcing, ${\rm{\Delta }}T/{\rm{\Delta }}R;$ the fractional radiative contribution from atmospheric CO₂, ${\rm{\Delta }}R/{\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}};$ and the dependence of radiative forcing from atmospheric CO₂ on carbon emissions, ${\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}/{\rm{\Delta }}I$ (depicted in figure 1(b) by red, grey and blue arrows respectively). This definition of the TCRE for all radiative forcings shares the same dependence of the radiative forcing from CO₂ on cumulative carbon emissions, ${\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}/{\rm{\Delta }}I,$ as appearing in the original TCRE definition in (2), but is now generalised to include the non-CO₂ radiative forcing contribution.

Our aim is now to assess the behaviour of the TCRE on centennial timescales using a combination of ocean theory and diagnostics of two Earth System Models, GENIE only including radiative forcing from atmospheric CO₂ and IPSL-CM5A-LR including CO₂ and non-CO₂ radiative forcing.

Our ocean theory is only appropriate for the dependence of surface warming on radiative forcing, ${\rm{\Delta }}T/{\rm{\Delta }}R$ and the dependence of radiative forcing from atmospheric CO₂ on carbon emissions, ${\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}/{\rm{\Delta }}I.$ The diagnostics of the TCRE and TCRE_{all R} using (2) and (5) respectively are automatically the same for GENIE, but differ for IPSL-CM5A-LR. On centennial and millennial timescales, we expect that the climate response is dominated by the effect of carbon emissions, so that the TCRE and TCRE_{all R} become similar to each other. However, on shorter timescales, the TCRE and TCRE_{all R} differ from each other due to the effects of other forcing agents, such as aerosols and non-CO₂ greenhouse gases.

Our framework defining the TCRE and TCRE_{all R} in (2) and (5) respectively is now combined with theoretical balances for a global heat balance and buffered carbon inventory following Goodwin et al (2015).

The global heat balance for climate change involves an increase in radiative forcing since the pre-industrial, ΔR(t) (W m⁻², positive downward) driving a climate response, involving additional outgoing longwave radiation, λΔT(t) (W m⁻²), from the increase in global-mean surface air temperature plus the net downward heat flux into the climate system, N(t) (W m⁻²) (Gregory et al 2004, Gregory and Forster 2008)

$$\begin{eqnarray}&&{\rm{\Delta }}R(t)=\lambda {\rm{\Delta }}T(t)+\varepsilon N(t),\end{eqnarray} \tag{ 6 }$$

where λ is the equilibrium climate parameter (W m⁻² K⁻¹) and $\varepsilon N(t)$ is the scaled net heat flux into the climate system. The net heat flux $N(t)$ is dominated by the ocean heat uptake, accounting for over 90% of the anthropogenic warming of the climate system (Church et al 2011). The net heat flux $N(t)$ is scaled in (6) by a non-dimensional parameter, ε, to take into account the enhanced effect of ocean heat flux in increasing global-mean surface temperature relative to global-mean radiative forcing (Hansen et al 1984, Winton et al 2010). This heat balance is rearranged to provide an expression for the dependence of surface warming on radiative forcing

$$\begin{eqnarray}&&\displaystyle \frac{\partial T}{\partial R}=\displaystyle \frac{1}{\lambda }\left(1-\displaystyle \frac{\varepsilon N(t)}{{\rm{\Delta }}R(t)}\right),\end{eqnarray} \tag{ 7 }$$

where the fractional form, ${\rm{\Delta }}T/{\rm{\Delta }}R,$ is replaced by a differential form as there is a functional relationship and the effective ocean heat flux is normalised by the radiative forcing, $\varepsilon N(t)/{\rm{\Delta }}R(t)$.

The buffered carbon inventory connects the logarithm of atmospheric CO₂ to the sum of the cumulative carbon emission, ΔI(t), plus the carbon undersaturation of the ocean, I_Usat(t) (PgC), minus the increase in the terrestrial carbon uptake, ΔI_ter(t) (PgC), all divided by the buffered carbon inventory, I_B (PgC) (Goodwin et al 2015):

$$\begin{eqnarray}&&{\rm{\Delta }}{{\rm{lnCO}}}_{2}(t)=\displaystyle \frac{1}{{I}_{{\rm{B}}}}({\rm{\Delta }}I(t)+{I}_{{\rm{Usat}}}(t)-{\rm{\Delta }}{I}_{{\rm{ter}}}(t)),\end{eqnarray} \tag{ 8 }$$

where CO₂ is the mixing ratio of atmospheric carbon dioxide (ppm), I_Usat(t) is how much carbon the ocean needs to take up to reach an equilibrium with the atmosphere and ${\rm{\Delta }}{I}_{{\rm{ter}}}(t)={I}_{{\rm{ter}}}(t)-{I}_{{\rm{ter}}}({t}_{{\rm{o}}})$ is the change in the residual terrestrial carbon sink since the pre-industrial era and I_B is the buffered carbon inventory for the atmosphere and ocean (Goodwin et al 2007). This buffered carbon inventory takes into account a positive feedback; increasing atmospheric CO₂ enhances ocean acidity and inhibits the ability of the ocean to take up more atmospheric CO₂ leading to an increasing fraction of the emitted carbon remaining in the atmosphere; thus, (8) expresses how atmospheric CO₂ increases exponentially with the sum of the cumulative carbon emission plus the ocean undersaturation and minus the terrestrial uptake.

The global heat balance (6) and buffered carbon inventory (8) are connected together via the radiative forcing from atmospheric CO₂, ${\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}(t),$ defined by the logarithm of atmospheric CO₂ (Myhre et al 1998)

$$\begin{eqnarray}&&{\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}(t)=a{\rm{\Delta }}{{\rm{lnCO}}}_{2}(t),\end{eqnarray} \tag{ 9 }$$

where the logarithm conveys how there is a saturating effect of increasing atmospheric CO₂ on radiative forcing.

Combing the buffered carbon balance (8) with the definition for radiative forcing from atmospheric CO₂ (9) then provides an expression for the dependence of radiative forcing from atmospheric CO₂ on carbon emissions (Goodwin et al 2015)

$$\begin{eqnarray}&&\displaystyle \frac{\partial {R}_{{{\rm{CO}}}_{2}}}{\partial I}=\displaystyle \frac{a}{{I}_{{\rm{B}}}}\left(1+\displaystyle \frac{{I}_{{\rm{Usat}}}(t)}{{\rm{\Delta }}I(t)}-\displaystyle \frac{{\rm{\Delta }}{I}_{{\rm{ter}}}(t)}{{\rm{\Delta }}I(t)}\right),\end{eqnarray} \tag{ 10 }$$

where the effects of the ocean carbon undersaturation and increase in terrestrial carbon store are normalised by the cumulative carbon emission, $({I}_{{\rm{Usat}}}(t)-{\rm{\Delta }}{I}_{{\rm{ter}}}(t))/{\rm{\Delta }}I(t).$ By combining the differential relations (7) and (10), the TCRE definition for all radiative forcing contributions in (5) becomes

$$\begin{eqnarray}&&{{\rm{TCRE}}}_{{\rm{all}}R}=\displaystyle \frac{a}{\lambda {I}_{{\rm{B}}}}\left(1-\displaystyle \frac{\varepsilon N(t)}{{\rm{\Delta }}R(t)}\right)\\ &&\quad \;\times \left(1+\displaystyle \frac{{I}_{{\rm{Usat}}}(t)}{{\rm{\Delta }}I(t)}-\displaystyle \frac{{\rm{\Delta }}{I}_{{\rm{ter}}}(t)}{{\rm{\Delta }}I(t)}\right)\left(\displaystyle \frac{{\rm{\Delta }}R(t)}{{\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}(t)}\right).\end{eqnarray} \tag{ 11 }$$

The TCRE_{all R} depends on the time-independent factors, $a/(\lambda {I}_{{\rm{B}}}),$ multiplied by the non-dimensional time-dependent terms contained within the three pairs of parentheses: the dependence of surface warming varying with ocean heat uptake; the dependence of radiative forcing from atmospheric CO₂ varying with ocean carbon undersaturation; and the fractional dependence of radiative forcing on atmospheric CO₂. As derived by Goodwin et al (2015), if there is only radiative forcing from CO₂, the TCRE simplifies to

$$\begin{eqnarray}&&{\rm{TCRE}}=\displaystyle \frac{{\rm{\Delta }}T}{{\rm{\Delta }}I}=\displaystyle \frac{a}{\lambda {I}_{{\rm{B}}}}\left(1-\displaystyle \frac{\varepsilon N(t)}{{\rm{\Delta }}R(t)}\right)\\ &&\quad \quad \quad \quad \;\;\times \left(1+\displaystyle \frac{{I}_{{\rm{Usat}}}(t)}{{\rm{\Delta }}I(t)}-\displaystyle \frac{{\rm{\Delta }}{I}_{{\rm{ter}}}(t)}{{\rm{\Delta }}I(t)}\right).\end{eqnarray} \tag{ 12 }$$

For a long-term equilibrium when the radiative forcing is only from atmospheric CO₂, the TCRE asymptotes to a response given by the time-independent factors a/(λI_B) (Williams et al 2012)

$$\begin{eqnarray}&&{\displaystyle \frac{{\rm{\Delta }}T}{{\rm{\Delta }}I}}_{t\to {\rm{equilib}}}=\displaystyle \frac{a}{\lambda {I}_{{\rm{B}}}}.\end{eqnarray} \tag{ 13 }$$

To evaluate the equilibrium response, $a$ (W m⁻²) is the coefficient for the radiative forcing dependence on atmospheric CO₂ (Myhre et al 1998, Forster et al 2013); $\lambda$ (W m⁻² K⁻¹) is the climate parameter (Gregory et al 2004) and equivalently ${\lambda }^{-1}$ is the equilibrium climate sensitivity (Knutti and Hegerl 2008); and I_B (PgC) is the buffered carbon inventory for the atmosphere and ocean (Goodwin et al 2007).

The buffered carbon inventory of the atmosphere and ocean, I_B, represents the accessible amount of carbon in the atmosphere and ocean, and takes into account how the buffering of the ocean carbonate system inhibits the release of carbon from the ocean to the atmosphere: I_B is defined for the pre-industrial era (Goodwin et al 2007) as

$$\begin{eqnarray}&&{I}_{{\rm{B}}}={I}_{{\rm{A}}}+V\;{{\rm{DIC}}}_{{\rm{sat}}}/B,\end{eqnarray} \tag{ 14 }$$

where I_A is the atmospheric inventory of carbon (PgC), ${{\rm{DIC}}}_{{\rm{sat}}}$ is the saturated ocean dissolved inorganic carbon (gC m⁻³) and B is the non-dimensional buffer factor, and V is the volume of the ocean (m³) (table 1). The buffer factor, B, represents the enhanced fractional changes in atmospheric CO₂, relative to the fractional changes in the saturated dissolved inorganic carbon ${{\rm{DIC}}}_{{\rm{sat}}},$ where $B=(\delta {{\rm{CO}}}_{2}/{{\rm{CO}}}_{2})/(\delta {{\rm{DIC}}}_{{\rm{sat}}}/{{\rm{DIC}}}_{{\rm{sat}}});$ B and ${{\rm{DIC}}}_{{\rm{sat}}}$ are evaluated using CO₂ and global-mean temperature, salinity, alkalinity and phosphate values for the pre-industrial ocean (Follows et al 2006, Williams and Follows 2011).

Table 1.  Climate variables in the two Earth System Models of different complexity.

		Earth System Model of Intermediate Complexity, GENIE	Earth System Model IPSL-CM5A-LR
Climate equilibrium parameter	λ	1.28 W m−2 K−1 (Goodwin et al 2015)	0.77 W m−2 K−1 based on a least-square regression (figure 3(a)) (assuming ε = 1.14)
Radiative forcing coefficient from CO2	a	5.77 W m−2	4.47 W m−2 (Andrews et al 2012)
Efficacy	ε	1.07 (Goodwin et al 2015)	1.14 (Geoffroy et al 2013)
Atmospheric carbon inventory at the preindustrial for 1850 at 280 ppmv (using a molar mass 1.77 × 1020 moles)	Ia	594 PgC	594 PgC
Temperature, salinity, alkalinity and Phosphate of global ocean at the pre-industrial	T, S, Alk, PO4	3.61 °C, 34.90, 2.43 mol m−3, 2.21 × 10−3 mol m−3	3.14 °C, 34.73, 2.43 mol m−3, 2.16 × 10−3 mol m−3
DIC of global ocean at the pre-industrial	${\rm{DIC}}$	(12 g mol−1) × 2.29 mol m−3	(12 g mol−1) × 2.347 mol m−3
Saturated DIC at the pre-industrial	${{\rm{DIC}}}_{{\rm{sat}}}$	(12 g mol−1) × 2.218 mol m−3	(12 g mol−1) × 2.221 mol m−3
Ocean saturated carbon inventory at the preindustrial (assuming ocean volume V of 1.341 × 1018 m3)	$V\;{{\rm{DIC}}}_{{\rm{sat}}}$	34 707 PgC	35 730 PgC
Effective global ocean buffer factor at the preindustrial	B	12.66	12.55
Buffered carbon inventory of the atmosphere and ocean	IB	3340 PgC	3440 PgC
Implied TCRE, ΔT/ΔI, at a long-term equilibrium	$a/(\lambda \;{I}_{{\rm{B}}})$	1.35 K(1000 PgC)−1	1.69 K(1000 PgC)−1

The Earth System Model of Intermediate Complexity (GENIE) is configured as a coarse-resolution atmosphere–ocean system, containing coupled circulation and biogeochemistry with 16 ocean layers and 36 × 36 equal-area grid elements over the globe (Ridgwell et al 2007). This version of GENIE includes climate feedbacks, in which increased CO₂ increases the radiative forcing and warms the climate; in this application of GENIE, sediment interactions are disabled. The model configurations are forced to reproduce historical CO₂ concentrations to 2005 and then to follow Representative Concentration Pathways (RCPs, Moss et al 2010) until 2100 for those RCPs with significant warming (RCP 4.5, 6.0 and 8.5).

IPSL-CM5A-LR is an ocean–atmosphere general circulation model including an explicit representation of the carbon cycle on land and in the ocean (Dufresne et al 2013). In this version, the atmospheric component (LMDZ) is integrated with 39 vertical levels and a horizontal resolution of 3.75° × 1.9°, and the oceanic component (NEMOv3.2) is integrated with 31 vertical levels and a horizontal resolution ranging from 0.5° to 2°. For the simulations diagnosed here, the model is forced with prescribed atmospheric CO₂ concentrations, following historical CO₂ values until 2005, and the different RCP from 2005 to 2100; RCP 2.6, 4.5, 6.0 and 8.5. Other forcings, such as land-use changes, other greenhouse gases and anthropogenic aerosols are also included.

The carbon cycle components, ORCHIDEE for the land (Krinner et al 2005) and PISCES for the ocean (Aumont and Bopp 2006), provide net carbon fluxes from the atmosphere to the terrestrial biosphere and the ocean, respectively. These fluxes include the net effect of changing atmospheric CO₂ and those of climate feedbacks. Compatible anthropogenic emissions are diagnosed a posteriori, using modelled air-to-sea and air-to-land carbon fluxes as well as imposed atmospheric CO₂ trajectories, as applied in Jones et al (2013).

The transient climate response is now assessed using GENIE, configured as an idealised atmosphere–ocean model; see Goodwin et al (2015) for further model details. There is only radiative forcing from atmospheric CO₂ with no changes to other radiative forcing agents, such as aerosols, and no changes in the terrestrial sink of carbon, so that the TCRE dependence in (12) simplifies to

$$\begin{eqnarray}&&{\rm{TCRE}}=\displaystyle \frac{{\rm{\Delta }}T}{{\rm{\Delta }}I}=\displaystyle \frac{a}{\lambda {I}_{{\rm{B}}}}\left(1-\displaystyle \frac{\varepsilon N(t)}{{\rm{\Delta }}R(t)}\right)\left(1+\displaystyle \frac{{I}_{{\rm{Usat}}}(t)}{{\rm{\Delta }}I(t)}\right).\end{eqnarray} \tag{ 15 }$$

Within GENIE, the equilibrium TCRE from $a/(\lambda {I}_{{\rm{B}}})$ is given by 1.35 K(1000 PgC)⁻¹, where a = 5.35 W m⁻², λ = 1.28 W m⁻² K⁻¹ and I_B = 3340 PgC (table 1). The efficacy factor weighting the effect of the ocean heat flux on surface temperature is 1.07 (table 1; Goodwin et al 2015).

The temporal evolution of the TCRE is determined by (i) how the dependence of surface warming on radiative forcing, ${\rm{\Delta }}T/{\rm{\Delta }}R,$ varies with the normalised ocean heat uptake, $\varepsilon N(t)/{\rm{\Delta }}R(t),$ versus (ii) how the dependence of radiative forcing from atmospheric CO₂ on carbon emissions, ${\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}/{\rm{\Delta }}I,$ varies with the normalised ocean undersaturation in carbon, ${I}_{{\rm{Usat}}}(t)/{\rm{\Delta }}I(t)$.

Within the GENIE model, the dependence of surface warming on radiative forcing, ${\rm{\Delta }}T/{\rm{\Delta }}R,$ increases in time (figure 2(a)). This increase in ${\rm{\Delta }}T/{\rm{\Delta }}R$ is due to changes in ocean heat uptake as the ocean interior warms and its temperature increases from its pre-industrial state; the ocean surface temperature then increases more rapidly for a specified increase in radiative forcing, since a smaller fraction of the radiative forcing is taken up by the ocean heat flux to warm the ocean interior. This response is equivalent to surface warming leading to a thinning of the surface mixed layer and increasing the stratification in the underlying ocean interior.

Zoom In Zoom Out Reset image size

The dependence of radiative forcing from atmospheric CO₂ on carbon emissions, ${\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}/{\rm{\Delta }}I,$ decreases in time (figure 2(b)). This decrease in ${\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}/{\rm{\Delta }}I$ is due to the ocean taking up carbon, so that the ocean carbon undersaturation decreases. The increase in radiative forcing from atmospheric CO₂ then becomes smaller for additional increases in emitted carbon with a smaller change in the logarithm of CO₂ induced per unit carbon emitted through the decrease in ocean undersaturation.

In consequence, there is a relatively small decrease in the TCRE (figure 2(c)) through a slightly larger decrease in ${\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}/{\rm{\Delta }}I$ being partly compensated by a smaller increase in ${\rm{\Delta }}T/{\rm{\Delta }}R.$ There is only a relatively weak sensitivity to emission pathway on this centennial timescale (different coloured lines in figure 1(a), left panel and figure 2).

In the more complex Earth System Model IPSL-CM5A-LR, the warming response is explored for four RCP emissions scenarios (figure 1(a), right panel). The climate projections are affected also by non-CO₂ radiative forcing, including changes from anthropogenic aerosols, non-CO₂ greenhouse gases, land-use changes and terrestrial changes in carbon storage. Accordingly, the TCRE is now diagnosed using the full expression in (11).

3.3.1. Equilibrium response

Our theory suggests that the TCRE asymptotes to an equilibrium response given by the time-independent factors $a/(\lambda {I}_{{\rm{B}}}),$ each of these input parameters differ slightly from those for GENIE. The buffered carbon inventory I_B is diagnosed as 3440 PgC, similar to the estimate of 3340 PgC for GENIE (table 1). The climate parameter is diagnosed as $\lambda =0.77$ W m⁻² K⁻¹ by solving a least-squares regression of the surface heat balance (Gregory et al 2004); comparing the time series of the radiative forcing minus ocean heat uptake, ${\rm{\Delta }}R-\varepsilon N$ (W m⁻²), versus surface temperature change, ΔT (K) (figure 3(a), table 2). Our estimate of the climate parameter, λ, is very close to estimates of 0.75, 0.76 and 0.79 W m⁻² K⁻¹ based on climate-model projections for an abrupt 4 × CO₂ increase, respectively, from Andrews et al (2012), Dufresne et al (2013) and Geoffroy et al (2013). The climate parameter, λ, is assumed to remain constant over time and is evaluated over the climate model integrations to 2100, rather than from an integration to an equilibrium state: the resulting values of λ vary with the RCP scenario (table 2), which might possibly reflect a time-dependence in its response (Senior and Mitchell 2000) or a sensitivity to regional changes in warming and ocean circulation that differ with each RCP (Armour et al 2013, Winton et al 2013).

Zoom In Zoom Out Reset image size

Table 2.  Estimates of the climate parameter λ from the Earth System Model IPSL-CM5a-LR for emission pathways: RCP2.6, RCP4.5, RCP6.0 and RCP8.5. The climate parameter is estimated from a least squares fit between the radiative forcing minus ocean heat uptake, ${\rm{\Delta }}R-\varepsilon N$ (W m⁻²) and surface temperature change ΔT (K) for an efficacy ε of 1.14 (Geoffrey et al 2013). The average value of λ for all RCPs is 0.77; all correlation coefficients are significant (r > 0.26 for a 99% confidence limit).

	Climate parameter	Correlation coefficient
Emission pathway	λ (W m−2 K−1)	r
RCP 2.6	1.02	0.78
RCP 4.5	0.76	0.92
RCP 6	0.68	0.86
RCP 8.5	0.63	0.97

The coefficient for the radiative forcing dependence on atmospheric CO₂, a, is taken as 4.47 W m⁻² from the effective radiative forcing diagnosed for a climate model projection with an abrupt 4 × CO₂ increase (Andrews et al 2012). This effective radiative forcing estimate is less than the expected theoretical value of 5.35 W m⁻² (Myhre et al 1998) and takes into account rapid adjustments in clouds and other tropospheric and land-surface changes (Forster et al 2013).

The diagnosed values of a, λ and I_B, then suggest an equilibrium dependence of surface warming to cumulative carbon emissions for the Earth System Model of 1.69 K(1000 PgC)⁻¹, slightly larger than the equilibrium dependence of 1.35 K(1000 PgC)⁻¹ for GENIE (table 1).

3.3.2. Transient response

To understand the transient response, the different terms in the global heat balance (6) and buffered carbon inventory (8) are diagnosed. The heat flux into the climate system, N(t), is equated with the ocean heat heat uptake, and diagnosed from the tendency in the global ocean heat content. The ocean carbon undersaturation, I_Usat(t), is diagnosed from the difference in the saturated DIC anomaly and the actual DIC anomaly over the global ocean, ${I}_{{\rm{Usat}}}(t)\quad =V({\rm{\Delta }}{{\rm{DIC}}}_{{\rm{sat}}}(t)-{\rm{\Delta }}{\rm{DIC}}(t))$.

There are temporal variations in the surface heat balance (6) over the 100 year integration. The radiative forcing, ΔR(t), is dominated by the contribution from atmospheric CO₂, ${\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}(t)$ (figure 3(b), black full and dashed lines for RCP8.5). The radiative forcing, ΔR(t), is partly offset by an ocean heat uptake, N(t) (blue line), and the remaining net forcing drives the surface climate response, λΔT(t) (red line) in figure 3(b); assuming ε = 1.14 from Geoffroy et al (2013). At the start of the integration, the climate response is slightly less than the ocean heat uptake, while by the end of the integration, the climate response is slightly larger than the ocean heat uptake. Thus, the normalised ocean heat uptake, $\varepsilon N(t)/{\rm{\Delta }}R(t),$ decreases in time in (11), leading to the dependence of surface warming on radiative forcing increasing in time.

There are likewise temporal changes in the buffered carbon balance (8), although the carbon inventory changes are noticeably smoother. The ocean carbon undersaturation, I_Usat(t) (blue line), is initially comparable to the cumulative carbon emission, ΔI(t) (red line), but becomes slightly smaller over the 100 year integration in figure 3(c). Thus, the normalised ocean undersaturation, I_Usat(t)/ΔI(t), reduces in time and there is also a relatively small increase in the terrestrial store of carbon, ΔI_ter (t) (figure 3(c), green line). Thus,$({I}_{{\rm{Usat}}}(t)-{\rm{\Delta }}{I}_{{\rm{ter}}}(t))/{\rm{\Delta }}I(t)$ reduces in time in (11), leading to the dependence of radiative forcing on carbon emissions decreasing in time.

Accordingly, there are larger centennial trends for the dependencies making up the TCRE_{all R}, than for the TCRE_{all R}: there is a long-term increase in the dependence of surface warming on radiative forcing, ${\rm{\Delta }}T/{\rm{\Delta }}R$ (figure 4(a)), a smaller decrease in the fractional dependence of radiative forcing from atmospheric CO₂, ${\rm{\Delta }}R/{\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}$ (figure 4(b)), and a larger decrease in the dependence of radiative forcing on carbon emissions, ${\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}/{\rm{\Delta }}I$ (figure 4(c)). The resulting TCRE_{all R} then only slightly decreases over the centennial timescale (figure 4(d)).

Zoom In Zoom Out Reset image size

There are though decadal changes in the TCRE_{all R} (figure 4(d)). The decadal variability in ${\rm{\Delta }}T/{\rm{\Delta }}I$ originates from decadal changes in the dependence of surface warming on radiative forcing, ${\rm{\Delta }}T/{\rm{\Delta }}R$ (figure 4(a)) from changes in ocean heat uptake (figure 3(b), blue line), and the fractional dependence of radiative forcing on atmospheric CO₂, ${\rm{\Delta }}R/{\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}$ (figure 4(b)) from the effects of aerosols and non-CO₂ greenhouse gases. In contrast, the dependence of radiative forcing from atmospheric CO₂ on carbon emissions, ${\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}/{\rm{\Delta }}I,$ varies relatively smoothly in time (figure 4(c)) due to the smooth changes in carbon emissions and ocean carbon undersaturation (figure 3(c), red and blue lines).

Our framework for the TCRE_{all R} highlights how there are broadly similar responses in the Earth System Models, GENIE and IPSL-CM5A-LR. The centennial trends of the TCRE_{all R} and its dependences have similar signs to each other in both Earth System Models (figures 2 and 4): both models show a positive trend in the dependence of surface warming on radiative forcing, a negative trend in the dependence of radiative forcing on carbon emissions, and a resulting slight negative trend in the TCRE. Thus, there is traceability between these Earth System Models of different complexity, as there are similar underlying trends in their response.

The exact values of the dependences differ though in each Earth System Model (table 3), as the models contain different representations of the physical circulation and biogeochemistry. The TCRE_{all R} is higher in the IPSL-CM5A-LR model, than in GENIE, and subsequently reduces by a greater amount over the next century (table 3). These differences in the TCRE_{all R} are due to (i) a larger dependence of the surface warming on radiative forcing in IPSL-CM5A-LR than in GENIE, and (ii) conversely a smaller dependence of the radiative forcing from atmospheric CO₂ on cumulative emissions in IPSL-CM5A-LR than in GENIE. There are also interannual and decadal differences in each model due to the IPSL-CM5A-LR containing radiative forcing contributions from aerosols and non-CO₂ greenhouse gases, as well as more complex ocean dynamics altering the ocean uptake of heat and carbon.

Table 3.  Climate dependences for two Earth System Models at 2005 and 2100 for different choices of emission pathways.

	Dependence of surface warming on radiative forcing, ${\rm{\Delta }}T/{\rm{\Delta }}R$		Dependence of radiative forcing from atmospheric CO2 on cumulative carbon emissions, ${\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}/{\rm{\Delta }}I$		Dependence of surface warming on cumulative carbon emissions, the TCREall R, ${\rm{\Delta }}T/{\rm{\Delta }}I$
	K (W m−2)−1		W m−2 (1000 PgC)−1		K (1000 PgC)−1
(a) Earth System model of Intermediate Complexity, GENIE
Year	2005	2100	2005	2100	2005	2100
RCP 4.5	0.50	0.60	5.00	3.98	2.48	2.38
RCP 6	0.50	0.56	5.00	3.93	2.48	2.19
RCP 8.5	0.50	0.55	5.00	3.58	2.48	1.95
(b) Earth System Model IPSL-CM5A-LR
Year	2005	2100	2005	2100	2005	2100
RCP 2.6	0.68	0.94	3.46	2.21	3.55	2.67
RCP 4.5	0.67	0.91	3.46	2.11	3.55	2.56
RCP 6	0.71	0.81	3.46	2.33	3.55	2.31
RCP 8.5	0.67	0.78	3.46	2.30	3.55	2.65

There are only slight differences in each of the climate dependences for the different choices of the RCP emission pathways over a century timescale (figures 1(a), 2 and 4; table 3).

There are two alternative approaches to our framework. Firstly, the TCRE has been previously explained in terms of the dependence of surface temperature on atmospheric CO₂, ${\rm{\Delta }}T/{\rm{\Delta }}{{\rm{CO}}}_{2},$ multiplied by the dependence of atmospheric CO₂ on cumulative emissions, ${\rm{\Delta }}{{\rm{CO}}}_{2}/{\rm{\Delta }}I$ (Matthews et al 2009, Gillett et al 2013). Their approach highlights how the TCRE is nearly constant due to partial compensation between changes in the dependence of surface temperature on CO₂ and changes in the air-borne fraction of emitted carbon.

Secondly, the sensitivities of climate models have been understood in terms of empirical parameters, α, β and γ, representing the sensitivity of temperature to atmospheric CO₂, and the sensitivity of carbon invetories to atmospheric CO₂ and temperature respectively (Friedlingstein et al 2006, Plattiner et al 2008). This approach has been used to understand the contributions of the different land and ocean inventories to carbon uptake and feedback on climate.

In our view, the connection to the underlying theory is more transparent in our framework, since there are clear dependences on the logarithm of atmospheric CO₂ drawing upon the buffered carbon inventory (8) and the definition of radiative forcing from atmospheric CO₂ in (9). While our framework includes a term accounting for changes in the terrestrial carbon sink, our theory is designed to make clearer the central contribution of the ocean, rather than drawing upon empirical relationships between changes in the land sinks of carbon (Friedlingstein et al 2006).

The long-term trends for the TCRE can be simply understood in terms of the heat and carbon uptake for an idealised representation of the atmosphere–ocean-terrestrial system. The additional heat supplied to the climate system is primarily taken up by the ocean, while the additional carbon is taken up by both the ocean and terrestrial system.

In order to understand how the TCRE is controlled, now consider how the climate response to carbon emissions is likely to alter in time:

(i) the additional heat supplied from an increase in radiative forcing is used to warm both the surface and ocean interior. As the ocean interior warms in time, a smaller proportion of the radiative forcing is taken by the interior and a larger proportion of the radiative forcing then warms the surface. Thus, the dependence of surface warming on radiative forcing, ${\rm{\Delta }}T/{\rm{\Delta }}R,$ is expected to increase in time as the ocean interior adjusts to a new equilibrium (figure 5(a)). Equivalently, the radiative forcing is likely to increase the stratification in time and lead to an increase in the dependence of surface warming on radiative forcing.

Zoom In Zoom Out Reset image size

(ii) For a given carbon emission, radiative forcing is initially expected to be large as most of the emitted carbon is in the form of atmospheric CO₂. The radiative forcing is then expected to decline as the excess atmospheric CO₂ is taken up by the ocean and terrestrial system. Thus, the dependence of radiative forcing from atmospheric CO₂ on cumulative carbon emissions, ${\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}/{\rm{\Delta }}I,$ is expected to decrease in time as the ocean and terrestrial system take up the excess atmospheric CO₂ (figure 5(b)).

(iii) The resulting surface warming response to cumulative carbon emissions (the TCRE) then only weakly varies, depending on the partial compensation between the dependences of surface warming on radiative forcing, ${\rm{\Delta }}T/{\rm{\Delta }}R,$ and the radiative forcing from atmospheric CO₂ on emissions, ${\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}/{\rm{\Delta }}I$.

This inference supports the argument of Solomon et al (2009) as to why long-term irreversible climate change persists after the cessation of carbon emissions; the gradual reduction in radiative forcing from atmospheric CO₂ is partly compensated by a decline in ocean heat uptake, so that global warming is likely to continue to persist on a millennial timescale.

The decadal changes in the TCRE_allR can be understood via our relationship (11). The dependence of surface warming on radiative forcing, ${\rm{\Delta }}T/{\rm{\Delta }}R,$ is controlled by the heat flux from the atmosphere to the ocean weighted by the efficacy, such that $\frac{\partial T}{\partial R}=\frac{1}{\lambda }\left(1-\frac{\varepsilon N(t)}{{\rm{\Delta }}R(t)}\right).$ The magnitude and sign of the ocean heat flux (figure 3(b), blue line) can easily change on interannual to decadal timescales given changes in atmosphere and ocean heat storage. For example, there is a hiatus in surface warming for 2000–2010, which is attributed to an increase in ocean heat uptake (Guemas et al 2013, Watanabe et al 2013). These changes in ocean heat uptake might be associated with coupled atmosphere–ocean phenomena, such as the El Nino Southern Oscillation, or changes in ocean ventilation, particularly associated with formation of water masses in the North Atlantic and Southern Ocean.

The dependence of radiative forcing on the contribution from atmospheric CO₂, ${\rm{\Delta }}R/{\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}$ (figure 4(c)) can likewise easily alter through the release of atmospheric aerosols, particularly linked to volcanic and anthropogenic emissions (Ottera et al 2010, Booth et al 2012), and changes in other non-CO₂ greenhouse gases, such as methane (Pierrehumbert 2014).

The dependence of radiative forcing from CO₂ on carbon emissions, ${\rm{\Delta }}{R}_{{{\rm{CO}}}_{2}}/{\rm{\Delta }}I,$ is controlled by the carbon undersaturation of the ocean relative to the atmosphere and changes in the terrestrial sink of carbon, $\frac{\partial {R}_{{{\rm{CO}}}_{2}}}{\partial I}=\frac{a}{{I}_{{\rm{B}}}}\left(1+\frac{{I}_{{\rm{Usat}}}(t)}{{\rm{\Delta }}I(t)}-\frac{{\rm{\Delta }}{I}_{{\rm{ter}}}(t)}{{\rm{\Delta }}I(t)}\right).$ The carbon undersaturation of the ocean, I_Usat(t), only alters slowly in time (figure 3(c), blue line) and is less sensitive to the interannual and decadal changes in the carbon flux between the atmosphere and ocean, such as seen in climate model simulations of natural variability in air-sea CO₂ and O₂ fluxes (Resplandy et al 2015). The terrestrial sink probably weakly increases in time, ΔI_ter(t) (figure 3(c), green line), although there is a large range in the magnitude and sign in the projected terrestrial response for different climate models (Friedlingstein et al 2006).