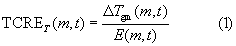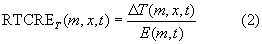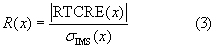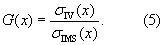Abstract
Cumulative CO2 emissions are near linearly related to both global and regional changes in annual-mean surface temperature. These relationships are known as the transient climate response to cumulative CO2 emissions (TCRE) and the regional TCRE (RTCRE), and have been shown to remain approximately constant over a wide range of cumulative emissions. Here, we assessed how well this relationship holds for seasonal patterns of temperature change, as well as for annual-mean and seasonal precipitation patterns. We analyzed an idealized scenario with CO2 concentration growing at an annual rate of 1% using data from 12 Earth system models from the Coupled Model Intercomparison Project Phase 5 (CMIP5). Seasonal RTCRE values for temperature varied considerably, with the highest seasonal variation evident in the Arctic, where RTCRE was about 5.5 °C per Tt C for boreal winter and about 2.0 °C per Tt C for boreal summer. Also the precipitation response in the Arctic during boreal winter was stronger than during other seasons. We found that emission-normalized seasonal patterns of temperature change were relatively robust with respect to time, though they were sub-linear with respect to emissions particularly near the Arctic. Moreover, RTCRE patterns for precipitation could not be quantified robustly due to the large internal variability of precipitation. Our results suggest that cumulative CO2 emissions are a useful metric to predict regional and seasonal changes in precipitation and temperature. This extension of the TCRE framework to seasonal and regional climate change is helpful for communicating the link between emissions and climate change to policy-makers and the general public, and is well-suited for impact studies that could make use of estimated regional-scale climate changes that are consistent with the carbon budgets associated with global temperature targets.

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence.
Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Cumulative CO2 emissions have been shown to be a useful metric to estimate the global-mean temperature change resulting from human CO2 emissions (Matthews et al 2009, Allen et al 2009). A growing body of research has confirmed that global temperatures respond approximately linearly to cumulative emissions (Matthews et al 2009, Gillett et al 2013, Collins et al 2013, Leduc et al 2015) which has led to the formal definition of this relationship as the 'transient climate response to cumulative CO2 emissions' (TCRE) (Gillett et al 2013, Collins et al 2013). Estimates of the TCRE have now been widely used to compare model responses to cumulative emissions, as well as to estimate the total allowable emissions (or carbon budgets) associated with different levels of global-mean temperature change (Meinshaisen et al 2009, Zickfeld et al 2009, Friedlingstein et al 2014, Rogelj et al 2016).
While useful to inform efforts to meet climate mitigation targets such as 2 °C of global warming, the TCRE is limited in its ability to estimate the likelihood of climate impacts that manifest at the local (rather than global) scale. To expand the utility of the TCRE framework for climate impact assessments, Leduc et al (2016) recently demonstrated that regional changes in annual-mean temperature can also be linearly related to cumulative CO2 emissions. This analysis suggests that there is considerable potential to quantify regional TCRE (or RTCRE) values based on the patterns of climate response to cumulative emissions as an extension of the current global TCRE framework.
Furthermore, there is reason to expect that seasonal temperature change patterns, as well as patterns of annual-mean and seasonal precipitation, might also scale approximately linearly as a function of cumulative emissions. For many years, researchers have employed a technique known as pattern-scaling to estimate the regional temperature and precipitation changes associated with a given level of global mean warming (Santer et al 1990, National Research Council 2011, Tebaldi and Arblaster 2014). This technique is premised on the finding that climate patterns normalized by global-mean temperature remain approximately constant across a wide range of global temperature changes, which has been shown to hold for both annual-mean and seasonal patterns of both temperature and precipitation (National Research Council 2011, Tebaldi and Arblaster 2014, Mitchell 2003). Given a linear global temperature response to cumulative emissions, we therefore expect that it should be possible to extend the pattern-scaling approach from global-mean temperature to cumulative emissions, and apply this to both annual-mean and regional temperature and precipitation change patterns.
In this paper, we calculate annual-mean and seasonal regional temperature and precipitation responses to cumulative CO2 emissions based on an ensemble of models from the Coupled Model Intercomparison Project Phase 5 (CMIP5) (Taylor et al 2012). In addition to the RTCRE patterns, we quantify the robustness of the patterns in terms of inter-model spread, calculate the contribution of internal variability to inter-model spread, and assess to what extent these RTCRE patterns remain stable over time.
2. Methods
We used simulation data from the Coupled Model Intercomparison Project Phase 5 (CMIP5) (Taylor et al 2012). Specifically, we analyzed temperature and precipitation data from a scenario where CO2 concentration was rising annually by 1 percent from preindustrial levels (about 285 ppm) to fourfold this level after 140 years (experiment 1pct CO2) (Gillett et al 2013). As non-CO2 forcings were not considered in this experiment, it allows an excellent opportunity to calculate the effects of cumulative CO2 emissions alone. We used data from 12 earth system models; this model ensemble (table 1) was the same as that used by Leduc et al (2016), and for each model, only one realization of the experiment was available. In addition to using annual mean values (ANN), we did our analysis using also the means over four seasons: December–January–February (DJF), March–April–May (MAM), June–July–August (JJA), and September–October–November (SON). Regional changes in temperature and precipitation were averaged seasonally, but the scaling was still done using annual global total CO2 emissions.
The data processing methodology that we used is based on that of Leduc et al (2016). To study the global mean response, we evaluated the TCRE for temperature (TCRET) as:
where ΔTgm(m,t) is change in global mean temperature for model m at time t, and E(m, t) is the diagnosed cumulative CO2 emissions. The metric for precipitation (TCREP) was calculated in the same way as a ratio of change in global mean precipitation and cumulative emissions. We evaluated TCRE by comparing the means over 20-year average windows at the start of the simulation and at the time of doubling of CO2 concentration, using the model ensemble mean as the best estimate of the TCRE.
RTCRE for temperature (RTCRET) was evaluated for each model m, grid-cell x, and time t as:
where ΔT is the local change in temperature and E is the diagnosed cumulative CO2 emissions. The metric for precipitation (RTCREP) was calculated in the same way. As for global mean response, we used 20-year average windows centered at the time of doubling of CO2 concentration to evaluate the annual and seasonal means local changes, which is standard practice when evaluating climate change patterns. As for TCRE, we used the model ensemble mean as the best estimate for RTCRE. We calculated the spatial multi-model means by first interpolating all model data onto the grid of CanESM2 (2.8° of resolution).
To test whether the RTCRE stays constant over time, we calculated RTCRE for different 20-year windows relative to a same reference period (the first 20 years of the time series). We then show to what extent the zonal mean temperature and relative precipitation change remains stable over the 140 year duration of these simulations.
To assess the robustness of the climate change patterns, we calculated the ratio of the RTCRE and inter-model spread defined as:
where RTCRE(x) is the ensemble mean RTCRE change in location x and σIMS(x) is the standard deviation of RTCRE in the model ensemble. Both are evaluated at the time of doubling of the CO2 concentration as described above. The ratio is basically a signal to inter-model spread ratio, which is a convenient measure since the inter-model spread is often the largest where the signal is also large (Leduc et al 2016).
The previous measure of robustness can be interpreted as a standard signal to noise ratio in cases where the internal variability dominates the inter-model spread. To account for this effect, we calculated how the internal variability of the climate affects the RTCRE. As in Leduc et al (2016), we estimated,using the variance inflation factor from Wilks (2011), that over a N-year period, the effect of internal variability on RTCRE is:
where σ1(x)2 is the inter-annual variance of the detrended time series of annual mean temperature or relative change in precipitation with respect to the 20 year reference period. E is the cumulative CO2 emissions at the time of doubling of the CO2 concentration, and ϕ(x) is autocorrelation of the detrended time series with lag of one year. Autocorrelation with lag of two years was negligible for both variables, and therefore higher-order terms are not needed to calculate the internal variability. We detrended using a fourth-order polynomial fit (Hawkins and Sutton 2009, Leduc et al 2016). To quantify the contribution of the internal variability to the inter-model spread, we thus calculated the ratio of the effect of internal variability on the RTCRE to the inter-model spread in RTCRE:
3. Results
3.1. Annual mean temperature and precipitation response
Figures 1(a) and (b) show the change in global mean temperature and precipitation as a function of cumulative CO2 emissions for all 12 models and for the ensemble mean. The plots also contain straight lines representing ensemble mean TCRE at the time of doubling of CO2 concentration. In general, models with a strong temperature response had also a strong precipitation response. The ensemble mean TCRET and TCREP were 1.68 °C per Tt C and 2.5% per Tt C, respectively. Following the convention established in previous works (Matthews et al 2009, Gillett et al 2013, Leduc et al 2015 and 2016), these values were calculated as a change (in temperature or precipitation) per cumulative CO2 emissions at the time when the atmospheric CO2 concentration has doubled its initial concentration for each model individually before calculating the ensemble mean. Although evaluating TCRE at the time of doubling of CO2 concentration has been shown to be more stable than if it is calculated at a certain amount of cumulative emissions (Leduc et al 2015), the ensemble mean was very similar using both of these two methods (compare solid and dashed black lines in figures 1 (a) and (b)).
Figure 1 Ensemble mean of annual TCRE for (a) temperature and (b) precipitation and RTCRE for (c) temperature (reproduced figure 1(a) from Leduc et al (2016) with hatching added) and (d) precipitation. Hatching indicates areas where ∣RTCRE∣ > 2σIMS. (c) Reprinted by permission from Macmillan Publishers Ltd: Nat. Clim. Change 6 474–8, copyright 2016.
Download figure:
Standard image High-resolution imageFigures 1(c) and (d) show the ensemble mean annual mean RTCRE for temperature and precipitation. As discussed in Leduc et al (2016), land areas and especially the Arctic showed a strong temperature response to CO2 emissions mainly due to sea-ice feedback (Kumar et al 2010, Screen and Simmonds 2010). RTCRET values were greater than two times the inter-model spread (σIMS) over most of the globe (hatched regions in figure 1(c)). Here we also show the RTCREP as a relative change in precipitation per Tt C emitted. The strongest positive response took place at the Equator in the Pacific Ocean and Northeastern Africa, where RTCREP was about 30%–40% per Tt C. Over land areas, precipitation decreased considerably (by 8%–32% per Tt C) in Southern Europe, Northwestern Africa, and Southern parts of North America. RTCREP was mostly positive (about 5–25% per Tt C) at both poles. Unlike for temperature, only over small regions RTCREP was greater than 2σIMS, indicating considerably lower robustness as discussed in more detail in section 3.4.
3.2. Seasonal temperature and precipitation response
Figures 2(a) and (b) show seasonal TCRET in DJF and in JJA, respectively. Global mean responses were fairly similar to annual mean response for all seasons in terms of both model spread and ensemble mean. TCRET was 1.72, 1.63, 1.64, and 1.73 °C per Tt C for DJF, MAM, JJA, and SON, respectively. See figures S1(a) and (c) available at stacks.iop.org/ERL/12/075002/mmedia for TCRET for MAM and SON, respectively.
Figure 2 Seasonal TCRET in (a) DJF and (b) JJA and seasonal RTCRET in (c) DJF and (d) JJA. Hatching indicates areas where ∣RTCRE∣ > 2σIMS.
Download figure:
Standard image High-resolution imageFigures 2(c) and (d) show the RTCRET during DJF and JJA, respectively. Arctic amplification was most visible during DJF, where the highest value of RTCRET was 8.9 °C per Tt C in some parts of the Arctic. Everywhere below latitude 50 °N, RTCRET was below 3.8 °C per Tt C. There was little variation inside the latitude band between 40 °S and 30 °N: the zonal mean RTCRET was between 1.3 and 1.6 °C per Tt C within this region. For other seasons, the zonal variability of TCRET was considerably lower but land-sea contrasts were still apparent. For JJA, RTCRET was below 3.3 °C per Tt C everywhere, with the largest values occurring in Northern Eurasia and over parts of the Southern Ocean.
TCREP was 2.66, 2.40, 2.22, and 2.55 % per Tt C for DJF, MAM, JJA, and SON, respectively. RTCREP for annual means (figure 1(b)), DJF (figure 3(a)), MAM (figure S2(b)), JJA (figure 3(b)), and SON (figure S2(d)) were relatively similar in mid-latitudes and near the Equator. The most significant example of seasonal variability was the stronger precipitation response in the Arctic during DJF and SON. RTCREP in the Arctic (above 60°N) was mostly around about 20%–40% per Tt C in DJF, whereas for other seasons the values were mostly below 24% per Tt C. There were clear seasonal differences also in Southern Africa: a slight positive response (0%–8% per Tt C) in DJF and mainly negative response in other seasons (up to about −20% per Tt C). Also parts of Australia, Northern America, and Southern America had a different sign of RTCREP in different seasons.
Figure 3 Seasonal TCREP in (a) DJF and (b) JJA and seasonal RTCRET in (c) DJF and (d) JJA. Hatching indicates areas where ∣RTCRE∣ > 2σIMS.
Download figure:
Standard image High-resolution imageAs discussed in section 3.4 and shown with the limited extent of the hatched areas in figures 3(c) and (d) and figures S3(b) and (d), precipitation response had larger inter-model spread and was more sensitive to interannual variability than the temperature response. Therefore, the results on precipitation should be interpreted with caution.
3.3. Stability of climate change patterns over time
Figure 4 shows zonal mean of RTCRE over time for both temperature and precipitation. RTCRET stayed relatively stable over time. However, there was clearly noticeable decrease especially in the Arctic region, but also elsewhere in both annual and seasonal mean values (figures 4(a)–(c), figures S3(a) and (b)). This general decrease is consistent with previous work that has shown that TCRE deviates from linearity at very high levels of cumulative emissions (e.g. Leduc et al 2015, Herrington and Zickfeld 2014) The larger decrease of RTCRET in the Arctic can be attributed mostly to the weakening of the sea-ice albedo feedback (Leduc et al 2016). Although the Arctic amplification manifested mostly during DJF, the relative decrease with respect to time of zonal mean of RTCRE was similar for all DJF and JJA, suggesting that seasonal sea-ice albedo feedback changes are of comparable magnitude to the annual-mean change.
RTCREP stayed also relatively constant over time (figures 4(d) and (e), figures S3(c) and (d)). Different seasons had changes partly in opposite directions that made the annual mean RTCREP more stable. For example, in DJF, precipitation increase over the Arctic was stronger at later years, and weaker in SON. There was also some non-monotonic behavior in the precipitation response. During JJA, at latitudes around 50 °N, precipitation response was positive for the time window of the years 20–40, then negative again for the years 40–80, and changed again to positive for the rest of the experiment. At least part of this variation of sign was related to noise from the early years when both the signal and the emissions were small. Therefore, we show results beginning from the years 60–80 in figure 4. In general, there was not such a clear trend for precipitation as seen in the decreased temperature response over time.
Figure 4 Ensemble mean of zonal mean RTCRE for temperature for (a) annual means, (b) DJF, (c) JJA, and for precipitation in (d) annual means, (e) DJF, and JJA.
Download figure:
Standard image High-resolution image3.4. Robustness of RTCRE patterns and the contribution of internal variability
In the following, the ratio of RTCRET to inter-model spread (RT, equation (3)) is used as a measure of robustness of the models' climate change patterns. In general, models agreed relatively well in their RTCRET patterns within the mid-latitudes and the Equator (RT mostly between 4 and 8, see figures 5(a)–(c)). Even though the signal in the annual means (figure 1(c)) and in DJF (figure 2(c)) was largest at high latitudes, also the model spread was large and thus RT values were lower there than at mid-latitudes and the RTCRET values were lower than 2σIMS. Patterns show important disagreements in the Southern Ocean and in the poles (RT mostly below 3). figures 5(d)–(f) show the ratio of internal variability to the inter-model spread (GT, equation (5)) for temperature. Relative importance of the internal variability was considerably higher for seasonal means than for the annual mean. Especially in North America, Australia, and Europe in DJF, the internal variability component was important relative to the whole inter-model spread with values of GT being around 1 (note that GT occasionally exceeded 1, because one ensemble member per model is not enough to capture all internal variability and therefore there is some sampling error that affect the evaluation of equations (4) and (5)). In the areas where internal variability dominated the inter-model spread, more (than 1) ensemble members for individual models would help to produce more robust patterns. Conversely, in regions where internal variability was small compared to the inter-model spread, having more members would likely not increase the robustness of the climate change patterns. Rather, the latter case refers to the situation where an improvement of the patterns involves a reduction of the overall uncertainty in regional climate sensitivity. In JJA, the contribution of internal variability to the inter-model spread was small over most of land areas with exception of Australia, Uruguay, and eastern part of the United States.
Figure 5 The robustness of the RTCRE patterns and the contribution of internal variability to inter-model spread. The first two rows show the robustness (ratio of ensemble mean RTCRE to inter-model spread of RTCRE for temperature, RT) for (a) annual means (ANN), (b) DJF, (c) JJA, and ratio of ensemble mean of the internal variability of RTCRE to the ensemble standard deviation of RTCRE (GT) for (d) annual means, (e) DJF, and (f) JJA. The two bottom rows show the robustness for precipitation (RP) for (g) annual means, (h) DJF, (i) JJA, and ratio of the ensemble mean of the internal variability of RTCRE to the ensemble standard deviation of RTCRE (GP) for (j) annual means, (k) DJF, and (l) JJA.
Download figure:
Standard image High-resolution imageThe robustness (RP) (figures 5(g)–(i)) was considerably lower for precipitation than for temperature. The values for RP were mostly below 3, which means that the signal is relatively weak compared to the model spread over almost all regions. In particular, in most regions where RP was smaller than 0.5, less than 75% of the models agreed on the sign of the change. The robustness was higher in Southern Europe (where precipitation decreased) during JJA and in Siberia and Hudson Bay (where precipitation increased) during DJF with RP values of about 2–4
Internal variability also had a large effect on the robustness of the TCREP metric (figures 5(j)–(l)). Already for the annual results, the ratio between the effect of internal variability on RTCREP and inter-model spread (GP) was over 0.8 over large regions reaching values of over 3 in certain areas. Note that regions with GP > 1 were larger for precipitation, because internal variability was more difficult to calculate accurately for precipitation than for temperature. The large effect of internal variability was clearly visible, when we plotted the regional change in precipitation against cumulative CO2 emissions over Giorgi regions (figure S4, Giorgi and Francisco 2000). For some regions, such as Australia (figure S5(a)), Sahara (figure S5(o)), Central Asia (figure S5(s)), it was practically impossible to evaluate the mean RTCREP because of the noise generated by internal variability in these low-precipitation regions. Means calculated over larger areas are more likely to be stable. As the Giorgi regions had different areas, ranking of regions with similar amount of noise should be done with caution.
Internal variability had an even larger role in the seasonal analysis. Regions with GP > 1 were larger and the values of GP were considerably greater everywhere compared to the annual results (figures 5(j)–(l)).The noise from internal variability was also very evident in the regional mean plots (figures S6–7), suggesting that it may be difficult to detect the effect of cumulative CO2 emissions on seasonal precipitation changes over most areas. However, there were some exceptions that show a more robust relationship, notably Greenland (figure S6(i) and figure S7(i)), Alaska (figure S6(h) and figure S7(h)), and North Asia (in JJA, figure S7(u)) had all clear increase in precipitation.
4. Discussion
The patterns of temperature and precipitation change scaled with cumulative CO2 emissions look visually very similar to those scaled with global mean temperature change (Tebaldi and Arblaster 2014). This is not surprising, given the near linear relationship between cumulative emissions and global mean temperature change as well as the consistent use of CMIP5 data (although using different scenarios and different model ensembles). This gives us confidence that our approach can be presented as a robust and straightforward extension of established and widely used pattern-scaling techniques.
Scaling climate change patterns with cumulative CO2 emissions rather than global mean temperature provides a more direct link between human actions and climate change. Estimating global mean temperature change with TCRE provides an easy-to-understand way of framing the climate response to CO2 emissions. Our work here, together with Leduc et al (2016) presents a generalized TCRE framework, which links cumulative CO2 emissions directly to regional and seasonal change in temperature and precipitation. With traditional pattern scaling with global mean temperature, a simple climate model is required to predict the evolution of the global mean temperature according to a given amount of CO2 emissions (e.g. Goodwin et al 2015). The generalized TCRE framework presented here provides a simple method to link emissions to expected climate change based simply on estimates of anticipated cumulative emissions associated with a given scenario, therefore removing the need to use a simple climate model before pattern scaling.
In theory, this extended TCRE framework could be improved further by employing more advanced methods of pattern scaling. For example, the Time Shift Approach (Herger et al 2015) could be used in almost identical way to the approach we have used here. In this method, the climate change patterns at certain amount of cumulative CO2 emissions would be directly taken from another simulation at a time of the equivalent cumulative CO2 emissions. This would preserve the internal consistency of temperature and precipitation patterns and implicitly take into account non-linearities involved in the retreat of Arctic sea ice.However, the improved accuracy would reducethe conceptual simplicity of scaling climate change patterns with cumulative CO2 emissions and make it less usable for climate impact studies.
Our analysis here was based on CO2- only forcing scenarios. The role of non- CO2 greenhouse gases, aerosols, and land-use change could be evaluated by comparing the results here to analysis of the RCP scenarios with other forcings included. This comparison will be addressed in future work.
5. Conclusions
We analyzed data from an ensemble of 12 CMIP5 models to assess to what extent regional and seasonal changes in temperature and precipitation can be described with a linear relationship to cumulative CO2 emissions. Overall, seasonal RTCRET was a fairly robust measure across models (signal was greater than two inter-model standard deviations over most of the globe), time and emissions. Thus, cumulative CO2 emissions can be used to predict temperature change both at global and regional scale for different seasons with almost similar robustness as for the annual means.
For precipitation the picture is more complicated. Although global total precipitation change scaled well with cumulative CO2 emissions for both annual and seasonal means, the regional change in precipitation was much more uncertain. First, disagreements between different models were large, even on the sign of change. Second, large internal variability made it difficult to extract a clear signal. This was true even when averaged over large regions. This large role of internal variability in precipitation response is, however, not specific to scaling the precipitation response with cumulative CO2 emissions. The same lack of robustness applies to the patterns scaled with global mean temperature change (Tebaldi and Arblaster 2014), and our results support the hypothesis by Tebaldi and Arblaster (2014) that internal variability can contribute to model disagreements even when 20 year averages are used.
Our analysis demonstrates that cumulative CO2 emissions can be linearly linked to regional and seasonal changes in temperature and to some degree also to changes in precipitation. This relationship can be used in assessing carbon budgets (van Vuuren et al 2016) also at regional and seasonal level, and in climate impact studies without using even a simple climate model before pattern scaling, and is also a useful concept in communicating with the general public about how climate will respond to continued anthropogenic CO2 emissions.
Table 1. CMIP5 models and the institutions that provided the model data used in this study.
| Model name | Modeling Center or Group |
|---|---|
| BNU-ESM | College of Global Change and Earth System Science, Beijing Normal University |
| CanESM2 | Canadian Centre for Climate Modelling and Analysis |
| CESM1-BGC | Community Earth System Model Contributors |
| HadGEM2-ES | Met Office Hadley Centre (additional HadGEM2-ES realizations contributed by Instituto Nacional de Pesquisas Espaciais) |
| INM-CM4 | Institute for Numerical Mathematics |
| IPSL-CM5A-LR | Institut Pierre-Simon Laplace |
| IPSL-CM5A-MR | Institut Pierre-Simon Laplace |
| IPSL-CM5B-LR | Institut Pierre-Simon Laplace |
| MIROC-ESM | Japan Agency for Marine-Earth Science and Technology, Atmosphere and Ocean Research Institute (The University of Tokyo), and National Institute for Environmental Studies |
| MPI-ESM-LR | Max-Planck-Institut für Meteorologie (Max Planck Institute for Meteorology) |
| MPI-ESM-MR | Max-Planck-Institut für Meteorologie (Max Planck Institute for Meteorology) |
| NorESM1-ME | Norwegian Climate Centre |
Acknowledgments
A.-I. Partanen was supported by a research grant from Emil Aaltonen Foundation. We acknowledge the World Climate Research Programme's Working Group on Coupled Modelling, which is responsible for CMIP, and we thank the climate modeling groups (listed in table 1 of this paper) for producing and making available their model output. For CMIP the US Department of Energy's Program for Climate Model Diagnosis and Intercomparison provides coordinating support and led development of software infrastructure in partnership with the Global Organization for Earth System Science Portals.