Journal of Physics A: Mathematical and Theoretical

We develop a method based on martingales to study first-passage problems of time-additive observables exiting an interval of finite width in a Markov process. In the limit that the interval width is large, we derive generic expressions for the splitting probability and the cumulants of the first-passage time. These expressions relate first-passage quantities to the large deviation properties of the time-additive observable. We find that there are three qualitatively different regimes depending on the properties of the large deviation rate function of the time-additive observable. These regimes correspond to exponential, super-exponential, or sub-exponential suppression of events at the unlikely boundary of the interval. Furthermore, we show that the statistics of first-passage times at both interval boundaries are in general different, even for symmetric thresholds and in the limit of large interval widths. While the statistics of the times to reach the likely boundary are determined by the cumulants of the time-additive observables in the original process, those at the unlikely boundary are determined by a dual process. We obtain these results from a one-parameter family of positive martingales that we call Perron martingales, as these are related to the Perron root of a tilted version of the transition rate matrix defining the Markov process. Furthermore, we show that each eigenpair of the tilted matrix has a one-parameter family of martingales. To solve first-passage problems at finite thresholds, we generally require all one-parameter families of martingales, including the ones that are not positive. We illustrate this by solving the first-passage problem for run-and-tumble particles exiting an interval of finite width.

In this work, we solve the Schrödinger equation of a particle restricted to move on a cone surface of finite height under the influence of an Aharonov–Bohm magnetic field. The energy eigenvalues and their respective wave functions are obtained analytically as a function of the radial distance from the apex and the apex angle. We compute the Shannon entropy in configuration and momentum space for the ground and the first excited states as a function of the slant height and the apex angle. In the absence of magnetic flux the states (n,m) and (n,−m) have identical Shannon entropies, but for non-zero fluxes the Shannon entropies of these states are different, their values depending on the state, the apex angle and the value of the magnetic flux.

Reaction-diffusion processes are the foundational model for a diverse range of complex systems, ranging from biochemical reactions to social agent-based phenomena. The underlying dynamics of these systems occur at the individual particle/agent level, and in realistic applications, they often display interaction with their environment through energy or material exchange with a reservoir. This requires intricate mathematical considerations, especially in the case of material exchange since the varying number of particles/agents results in 'on-the-fly' modification of the system dimension. In this work, we first overview the probabilistic description of reaction-diffusion processes at the particle level, which readily handles varying number of particles. We then extend this model to consistently incorporate interactions with macroscopic material reservoirs. Based on the resulting expressions, we bridge the probabilistic description with macroscopic concentration-based descriptions for linear and nonlinear reaction-diffusion systems, as well as for an archetypal open reaction-diffusion system. Using these mathematical bridges across scales, we finally develop numerical schemes for open reaction-diffusion systems, which we implement in two illustrative examples. This work establishes a methodological workflow to bridge particle-based probabilistic descriptions with macroscopic concentration-based descriptions of reaction-diffusion in open settings, laying the foundations for a multiscale theoretical framework upon which to construct theory and simulation schemes that are consistent across scales.

Synchronization is an ubiquitous phenomenon in systems composed of coupled oscillators. While it is often beneficial to the system under consideration, there are nevertheless relevant examples where one would like to reduce it, e.g. in brain dynamics. Indeed although synchronization is essential to the good functioning of brain dynamics, hyper-synchronization can induce problems such as epilepsy seizures. Motivated by this problem, we study a pinning control scheme able to decrease synchronization in a system of coupled Kuramoto oscillators, by focusing on the determination of the best selection strategy for the controllers, i.e. capable to guarantee a lower synchronization level. We show that hubs are generally the most advantageous nodes to control, especially when the degree distribution is heterogeneous. Nevertheless in cases of homogeneous degree distribution having a large distance between pinned nodes, in term of network shortest path length, appears to be also a key factor. We challenge the analytical findings on both synthetic and empirical networks, e.g. brain connectome. Our results are in line with previous works that studied pinning control with the opposite goal, i.e. increasing synchronization. These observations shed light on an interesting universality of good practice of node selection disregarding the actual goal of the control scheme.

We calculate the effective electromagnetic Lagrangian up to the lowest-order corrections in the derivatives for two fermionic systems of interest in condensed matter physics in the linearized approximation of the tight-binding Hamiltonian near the Fermi level in the Brillouin zone: (i) the $(3+1)$ description of the simplest Weyl semimetal and (ii) the massive $(2+1)$ electrodynamics, which can serve as a model for the interface between two $(3+1)$ topological insulators. We employ the derivative expansion method which directly provides local effective Lagrangians and allows selecting from the outset both the powers of the electromagnetic potential to be considered together with the number of relevant derivatives. We find new higher-order derivative corrections to Carroll-Field-Jackiw electrodynamics. In general, the new terms we find either have a similar structure or constitute a relativistic generalization of some recent phenomenological proposals found in the literature. In this way, they should be incorporated into these proposals for assessing the relative significance of all the terms included up to a given order.

These notes were presented at the Young Researchers School (YRS) in Maynooth in April 2024 and provide an introduction to conformal field theory (CFT), boundary CFT and Defect CFT. This class is mostly self-contained and includes exercises with solutions. The first part of these notes is concerned with the basics of CFT, and was taught by the author during the pre-school for the YRS 2024. Here the aim is to convey the notion of conformal families, their fusion and the construction of partition functions. The second part of these notes is dedicated to boundaries and defects in CFT and was presented by the author at the main school. As far as boundaries are concerned, emphasis is placed on boundary operators and their state spaces, as well as the boundary state formalism with the Cardy constraint. Topological defects are discussed in analogy, i.e. defect state spaces and the relevant consistency constraint are derived. Verlinde lines are constructed as their simplest solution and their properties are inspected.

Quantum sensors are now universally acknowledged as one of the most promising near-term quantum technologies. The traditional formulation of quantum sensing introduces a concrete bound on ultimate precision through the so-called local sensing framework, in which a significant knowledge of prior information about the unknown parameter value is implicitly assumed. Moreover, the framework provides a systematic approach for optimizing the sensing protocol. In contrast, the paradigm of global sensing aims to find a precision bound for parameter estimation in the absence of such prior information. In recent years, vigorous research has been pursued to describe the contours of global quantum estimation. Here, we review some of these emerging developments. These developments are both in the realm of finding ultimate precision bounds with respect to appropriate figures of merit in the global sensing paradigm, as well as in the search for algorithms that achieve these bounds. We categorize these developments into two largely mutually exclusive camps; one employing Bayesian updating and the other seeking to generalize the frequentist picture of local sensing towards the global paradigm. In the first approach, in order to achieve the best performance, one has to optimize the measurement settings adaptively. In the second approach, the measurement setting is fixed, however the challenge is to identify this fixed measurement optimally.

More then 35 approaches to the Dirac equation derivation are presented. Various physical principles and mathematical methods are used. A review of well-known and not enough known contributions to the problem is given, unexpected and unconventional derivations are presented as well. Three original approaches to the problem suggested by the author are considered: (i) generalization of H. Sallhofer derivation, (ii) obtaining of massless Dirac equation from the Maxwell equations in a maximally symmetrical form, (iii) derivation of the Dirac equation with nonzero mass from relativistic canonical quantum mechanics of the fermion-antifermion spin s = 1/2 doublet. Today we are able to demonstrate new features of our derivations given in original papers. In some sense the important role of the Dirac equation in contemporary theoretical physics is demonstrated. A criterion for the usefulness of one or another derivation of the Dirac equation is established.

We review different exact approaches to string theory. In the context of the Green–Schwarz superstring, we discuss the action in curved backgrounds and its supercoset formulation, with particular attention to superstring backgrounds of the AdS₃ type supported by both Ramond–Ramond and Neveu–Schwarz–Neveu–Schwarz fluxes. This is the basis for the discussion of classical integrability, of worldsheet-scattering factorisation in the uniform lightcone gauge, and eventually of the string spectrum through the mirror thermodynamic Bethe ansatz, which for AdS₃ backgrounds was only derived and analysed very recently. We then illustrate some aspects of the Ramond–Neveu–Schwarz string, and introduce the formalism of Berkovits–Vafa–Witten, which has seen very recent applications to AdS₃ physics, which we also briefly review. Finally, we present the relation between M-theory in the discrete lightcone quantisation and decoupling limits of string theory that exhibit non-relativistic behaviors, highlighting the connection with integrable $T\bar{T}$ deformations, as well as the relation between spin-matrix theory and Landau–Lifshitz models.

This review is based on lectures given at the Young Researchers Integrability School and Workshop 2022 'Taming the string worldsheet' at NORDITA, Stockholm.

The quantum-mechanical transition amplitudes for atomic and molecular processes in strong laser fields are expressed in the form of multidimensional integrals of highly oscillatory functions. Such integrals are ideally suited for the evaluation by asymptotic methods for integrals. Furthermore, using these methods it is possible to identify, in the sense of Feynman's path-integral formalism, the partial contributions of quantum orbits, which are related to particular solutions of the saddle-point equations. This affords insight into the physics of the problem, which would not have been possible by only solving these integrals numerically. We apply the saddle-point method to various quantum processes that are important in strong-field physics and attoscience. The special case of coalescing or near-coalescing saddle points requires application of the uniform approximation. We also present two modifications of the saddle-point method, for the cases where a singular point of the subintegral function exactly overlaps with a saddle point or is located in its close vicinity. Particular emphasis is on the classification of the saddle-point solutions. This problem is solved for the one-dimensional integral over the ionization time, relevant for above-threshold ionization (ATI), while for two-dimensional integrals a classification by the multi-index 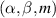$(\alpha,\beta,m)$ is introduced, which is particularly useful for the medium- and high-energy spectrum of high-order harmonic generation (HHG) and backward-scattered electrons (for high-order ATI). For the low-energy structures a classification using the multi-index 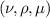$(\nu,\rho,\mu)$ is introduced for the forward-scattering quantum orbits. In addition to laser-induced processes such as ATI, HHG and high-order ATI, we consider laser-assisted scattering as an example of laser-assisted processes for which real solutions of the saddle-point equation exist. Particular attention is devoted to the quantum orbits that describe and visualize these processes. We also consider finite laser pulses, the semiclassical approximation, the role of the Coulomb field and the case of laser fields intense enough to lead into the relativistic regime.

Symmetry of non-Hermitian matrices underpins many physical phenomena. In particular, chaotic open quantum systems exhibit universal bulk spectral correlations classified on the basis of time-reversal symmetry^† (TRS^† ), coinciding with those of non-Hermitian random matrices in the same symmetry class. Here, we analytically study the spectral correlations of non-Hermitian random matrices in the presence of TRS^† with signs +1 and -1, corresponding to symmetry classes AI^† and AII^†, respectively. Using the fermionic replica non-linear sigma model approach, we derive n-fold integral expressions for the n^th moment of the one-point and two-point characteristic polynomials, valid for any matrix dimensions. We also study, in the limit of large matrix dimension, the replica limit n → 0 to derive the density of states and level-level correlations of non-Hermitian random matrices with TRS^†. We compare our analytical findings with numerical results.

In this work, we define a family of probability densities involving the generalized trigonometric functions defined by Drábek and Manásevich [1], which we name Generalized Trigonometric Densities. We show their relationship with the generalized stretched Gaussians and other types of laws such as logistic, hyperbolic secant, and raised cosine probability densities. We prove that, for a fixed generalized Fisher information, this family of densities is of minimal Rényi entropy. Moreover, we introduce generalized moments via the mean of the power of a deformed cumulative distribution. The latter is defined as a cumulative of the power of the probability density function, this second parameter tuning the tail weight of the deformed cumulative distribution. These generalized moments coincide with the usual moments of a deformed probability distribution with a regularized tail. We show that, for any bounded probability density, there exists a critical value for this second parameter below which the whole subfamily of generalized moments is finite for any positive value of the first parameter (power of the moment). In addition, we show that such generalized moments satisfy remarkable properties like order relation w.r.t. the first parameter, or adequate scaling behavior. Then we highlight that, if we constrain such a generalized moment,
both the Rényi entropy and generalized Fisher information achieve respectively their maximum and minimum for the generalized trigonometric densities. Finally, we emphasis that GTDs and cumulative moments can be used to formally characterize heavy-tailed distributions, including the whole family of stretched Gaussian densities.

We analyse a generalised Fokker-Planck equation in which both the nonlinear terms and the diffusivity are non-trivially dependent on the density and its derivatives. The key feature of the equation is its integrability, for it is linearisable through a Cole-Hopf transformation. We determine solutions of travelling wave and multi-kink type by resorting to a geometric construction in the regime of small viscosity. The resulting asymptotic solutions are time dependent Heaviside step functions representing classical (viscous) shock waves. As a result, line segments in the space of independent variables arise as resonance conditions of exponentials and represent shock trajectories. We then discuss fusion and fission dynamics exhibited by the multi-kinks by drawing parallels in terms of shock collisions and scattering processes between particles, which preserve total mass and momentum. Finally, we propose Backlund transformations and examine their action on the solutions to the equation under study

Perturbing transition rates in a steady nonequilibrium system, e.g. modeled by a Markov jump process, causes a change in the local currents. Their susceptibility is usually expressed via Green-Kubo relations or their nonequilibrium extensions. However, we may also wish to directly express the mutual relation between currents.
Such a nonperturbative interrelation was discovered by P.E. Harunari et al,
by applying algebraic graph theory showing the mutual linearity of currents over different edges in a graph. We give a novel and shorter derivation of that current relationship where we express the current-current susceptibility as a difference in mean first-passage times. It allows an extension to multiple currents, which remains affine but the relation is not additive.

We provide a mathematically and conceptually robust notion of quantum superpositions of graphs,
for the purpose of modelling a 'fully quantum internet' or states of geometry in quantum gravity.
We argue that, crucially, quantum superpositions of graphs require node names for their correct
alignment, which we demonstrate through a no-signalling argument. The need for node names was
often overlooked or disagreed upon in previous proposals. Still, node names should remain a fiducial
construct, serving a similar purpose to the labelling of points through a choice of coordinates in
continuous space. Graph renamings, aka isomorphisms, are understood as a change of coordinates
on the graph and correspond to a natively discrete analogue of continuous diffeomorphisms. We
postulate renaming invariance as a symmetry principle in discrete topology of similar weight to
diffeomorphism invariance in the continuous. We explain how to impose renaming invariance at the
level of quantum superpositions of graphs, in a way that still allows us to talk about an observable
centred at a specific node.

We develop a method based on martingales to study first-passage problems of time-additive observables exiting an interval of finite width in a Markov process. In the limit that the interval width is large, we derive generic expressions for the splitting probability and the cumulants of the first-passage time. These expressions relate first-passage quantities to the large deviation properties of the time-additive observable. We find that there are three qualitatively different regimes depending on the properties of the large deviation rate function of the time-additive observable. These regimes correspond to exponential, super-exponential, or sub-exponential suppression of events at the unlikely boundary of the interval. Furthermore, we show that the statistics of first-passage times at both interval boundaries are in general different, even for symmetric thresholds and in the limit of large interval widths. While the statistics of the times to reach the likely boundary are determined by the cumulants of the time-additive observables in the original process, those at the unlikely boundary are determined by a dual process. We obtain these results from a one-parameter family of positive martingales that we call Perron martingales, as these are related to the Perron root of a tilted version of the transition rate matrix defining the Markov process. Furthermore, we show that each eigenpair of the tilted matrix has a one-parameter family of martingales. To solve first-passage problems at finite thresholds, we generally require all one-parameter families of martingales, including the ones that are not positive. We illustrate this by solving the first-passage problem for run-and-tumble particles exiting an interval of finite width.

Symmetry of non-Hermitian matrices underpins many physical phenomena. In particular, chaotic open quantum systems exhibit universal bulk spectral correlations classified on the basis of time-reversal symmetry^† (TRS^† ), coinciding with those of non-Hermitian random matrices in the same symmetry class. Here, we analytically study the spectral correlations of non-Hermitian random matrices in the presence of TRS^† with signs +1 and -1, corresponding to symmetry classes AI^† and AII^†, respectively. Using the fermionic replica non-linear sigma model approach, we derive n-fold integral expressions for the n^th moment of the one-point and two-point characteristic polynomials, valid for any matrix dimensions. We also study, in the limit of large matrix dimension, the replica limit n → 0 to derive the density of states and level-level correlations of non-Hermitian random matrices with TRS^†. We compare our analytical findings with numerical results.

In this work, we solve the Schrödinger equation of a particle restricted to move on a cone surface of finite height under the influence of an Aharonov–Bohm magnetic field. The energy eigenvalues and their respective wave functions are obtained analytically as a function of the radial distance from the apex and the apex angle. We compute the Shannon entropy in configuration and momentum space for the ground and the first excited states as a function of the slant height and the apex angle. In the absence of magnetic flux the states (n,m) and (n,−m) have identical Shannon entropies, but for non-zero fluxes the Shannon entropies of these states are different, their values depending on the state, the apex angle and the value of the magnetic flux.

Reaction-diffusion processes are the foundational model for a diverse range of complex systems, ranging from biochemical reactions to social agent-based phenomena. The underlying dynamics of these systems occur at the individual particle/agent level, and in realistic applications, they often display interaction with their environment through energy or material exchange with a reservoir. This requires intricate mathematical considerations, especially in the case of material exchange since the varying number of particles/agents results in 'on-the-fly' modification of the system dimension. In this work, we first overview the probabilistic description of reaction-diffusion processes at the particle level, which readily handles varying number of particles. We then extend this model to consistently incorporate interactions with macroscopic material reservoirs. Based on the resulting expressions, we bridge the probabilistic description with macroscopic concentration-based descriptions for linear and nonlinear reaction-diffusion systems, as well as for an archetypal open reaction-diffusion system. Using these mathematical bridges across scales, we finally develop numerical schemes for open reaction-diffusion systems, which we implement in two illustrative examples. This work establishes a methodological workflow to bridge particle-based probabilistic descriptions with macroscopic concentration-based descriptions of reaction-diffusion in open settings, laying the foundations for a multiscale theoretical framework upon which to construct theory and simulation schemes that are consistent across scales.

We calculate the effective electromagnetic Lagrangian up to the lowest-order corrections in the derivatives for two fermionic systems of interest in condensed matter physics in the linearized approximation of the tight-binding Hamiltonian near the Fermi level in the Brillouin zone: (i) the $(3+1)$ description of the simplest Weyl semimetal and (ii) the massive $(2+1)$ electrodynamics, which can serve as a model for the interface between two $(3+1)$ topological insulators. We employ the derivative expansion method which directly provides local effective Lagrangians and allows selecting from the outset both the powers of the electromagnetic potential to be considered together with the number of relevant derivatives. We find new higher-order derivative corrections to Carroll-Field-Jackiw electrodynamics. In general, the new terms we find either have a similar structure or constitute a relativistic generalization of some recent phenomenological proposals found in the literature. In this way, they should be incorporated into these proposals for assessing the relative significance of all the terms included up to a given order.

We analyse a generalised Fokker-Planck equation in which both the nonlinear terms and the diffusivity are non-trivially dependent on the density and its derivatives. The key feature of the equation is its integrability, for it is linearisable through a Cole-Hopf transformation. We determine solutions of travelling wave and multi-kink type by resorting to a geometric construction in the regime of small viscosity. The resulting asymptotic solutions are time dependent Heaviside step functions representing classical (viscous) shock waves. As a result, line segments in the space of independent variables arise as resonance conditions of exponentials and represent shock trajectories. We then discuss fusion and fission dynamics exhibited by the multi-kinks by drawing parallels in terms of shock collisions and scattering processes between particles, which preserve total mass and momentum. Finally, we propose Backlund transformations and examine their action on the solutions to the equation under study

We provide an analytical formula for the volume ratio between bipartite X-states with positive partial transpose and all bipartite X-states. The result applies to arbitrary m×n-bipartite systems and the volume expressions are derived with respect to the Hilbert-Schmidt measure.

We argue that a consistent coupling of a quantum theory to gravity requires an extension of ordinary `first order' Riemannian geometry to second order Riemannian geometry, which incorporates both a line element and an area element.
This extension results in a misalignment between the dimension of the manifold and the dimension of the tangent spaces. In particular, we find that for a 4-dimensional spacetime, tangent spaces become 18-dimensional.
We then discuss the construction of physical theories within this framework, which involves the introduction of terms that are quadratic in derivatives in the action. On a flat spacetime, the quadratic sector is perpendicular to the first order sector and only affects the normalization of the path integral, whereas in a curved spacetime the quadratic sector couples to the first order sector. Moreover, we suggest that, despite the introduction of higher order derivatives, the Ostragradski instability may be avoided, due to an order mixing of the two sectors.
Finally, we comment on extensions to higher order geometry and on relations with non-commutative and generalized geometry.

We propose a method to design a magnetic field detector using a noisy two-qubit system. The system evolves under a noisy Heisenberg interaction Hamiltonian, and we investigate its behavior by calculating both the $l_1$-norm of quantum coherence and the return probability in the presence and absence of an external magnetic field. We allow for decoherence modeled by quasi-static charge noise in the exchange coupling of the two-qubit system and find that, while the magnetic field does not significantly influence the decoherence process, it introduces a distinct oscillation in the return probability over time. Importantly, the oscillation frequency is directly proportional to the strength of the applied magnetic field, providing a clear signature that can be used for magnetic field detection. These results point towards the feasibility of realizing a practical quantum-based magnetic field detector, with the ability to operate under noisy conditions while maintaining sensitivity to the field strength.

In this work, we make use of Lie algebraic methods to obtain the time evolution operator for an optomechanical system with linear and quadratic couplings between the field and the mechanical oscillator. Firstly, we consider the case of a non-driven system and find its exact time evolution operator, secondly we consider the case of a forced system whose time evolution operator is obtained in an approximate form. We confront our analytical results with a numerical simulation and find a good agreement between them.