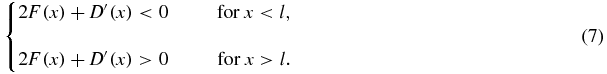The misconception of mean-reversion

As noted in the introduction the Ornstein–Uhlenbeck restoring force is quantified by the function F(x) = r(x − l). This force function is linear, and is thus rather particular and specific. If we replace the linear Ornstein–Uhlenbeck force function by a nonlinear force function we arrive at the Langevin stochastic differential equation

$$\begin{equation} \dot{X}( t) =-F\big( X( t) \big) +\sigma \dot{W} ( t). \end{equation} \tag{ 3 }$$

The Langevin equation (3) was introduced and pioneered by Paul Langevin [30], and is a cornerstone equation in the physical sciences [31–35].

As in the case of the Ornstein–Uhlenbeck process we consider the Langevin force function F(x) to be reverting toward a reversion level l. Namely, we consider the Langevin force function F(x) to be negative valued for x < l, and to be positive valued for x > l. The random process (X(t))_{t ⩾ 0} governed by the Langevin equation (3) is asymptotically stationary, and it converges in law (as t → ∞) to a stochastic steady state which manifests the 'stochastic balance' between the two opposing drivers—the Langevin restoring force and the perturbing white noise. The stationary distribution governing the steady state of the Langevin equation (3) is quantified by the probability density function

$$\begin{equation} \phi _{{\rm L}}( x) =c_{{\rm L}}\exp \bigg( -\frac{2}{\sigma ^{2}}\int ^{x}F( s) {\rm d}s\bigg) \end{equation} \tag{ 4 }$$

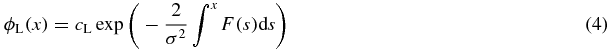
(−∞ < x < ∞; c_L being a normalizing constant). The density ϕ_L(x) is the stationary solution of the Fokker–Planck equation corresponding to the Langevin equation (3) [29]. The necessary and sufficient condition required to assure the validity of equation (4) is the integrability of the density ϕ_L(x) over the real line. The function V(x) = ∫^xF(s)ds (−∞ < x < ∞) appearing in equation (4) is a potential corresponding to the Langevin force function F(x).

The shape of the Langevin force function F(x)—negative valued below the reversion level, and positive valued above the reversion level—straightforwardly implies that the density ϕ_L(x) is unimodal, and that it attains its global maximum at the level l. Namely, the reversion level l is the mode of the density ϕ_L(x)—the stationary density of the Langevin dynamics. Thus, shifting from a linear Ornstein–Uhlenbeck restoring force to a nonlinear Langevin restoring force we conclude that:

• Mode-reversion always holds but, in general, mean-reversion is not bound to hold.
• In the special case where the Langevin stationary density is symmetric around its mode, and possesses a well-defined mean, then the mode and the mean coincide, and the reversion is to the common mode-mean.

In the case of the Ornstein–Uhlenbeck process the stationary distribution is Gaussian. The Gaussian distribution has finite moments, and its density is unimodal and is symmetric around its mode. Hence, the mean of the Gaussian distribution is well defined, and it coincides with the Gaussian mode. In contrast, in the case of general Langevin dynamics neither must the mean be well defined, nor does it necessarily coincide with the mode.

The following examples illustrate the 'failure of mean-reversion' in the context of Langevin dynamics. In all the examples we set, with no loss of generality, $\sigma =\sqrt{2}$.

Laplace example. Consider the nonlinear force function given by: F(x) = −p₋ for x < 0, and F(x) = p₊ for x > 0 (where p₋ and p₊ are positive parameters). The reversion level of this force function is the origin l = 0, and the resulting stationary density is Laplace: ϕ_L(x) = c_Lexp ( − p₋|x|) for x < 0, and ϕ_L(x) = c_Lexp ( − p₊|x|) for x > 0. This Laplace density is unimodal, it attains its mode at the origin, and it is symmetric around its mode if and only if p₋ = p₊. The mean of this Laplace density is (1/p₊) − (1/p₋). Thus, mean-reversion holds only in the symmetric scenario characterized by p₋ = p₊.

Student example. Consider the nonlinear force function F(x) = (1 + p)x/(p + x²) (where p is a positive parameter). The reversion level of this force function is the origin l = 0, and the resulting stationary density is Student: ϕ_L(x) = c_L/(1 + x²/p)^{(1 + p)/2}. The parameter value p = 1 yields a Cauchy–Lorentz density, and the parameter limit p → ∞ yields a Gauss density. This Student density is unimodal, it attains its mode at the origin, and it is symmetric around its mode. The mean of this Student density is ill-defined in the parameter range p ⩽ 1, and is zero in the parameter range p > 1. Thus, although this Student density is symmetric around its mode—the very notion of mean-reversion is well-defined only in the parameter range p > 1.

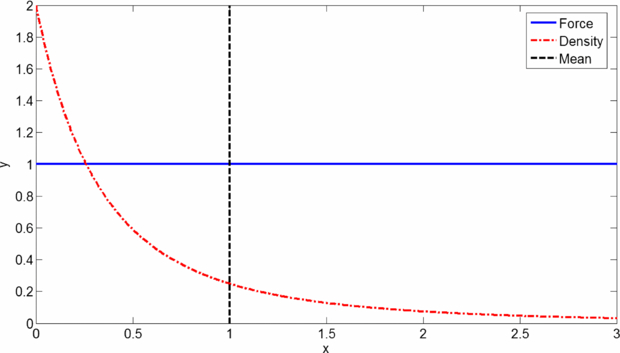
Gamma example. In this example the Langevin dynamics take place on the positive half-line (x > 0). Consider the nonlinear force function F(x) = 1 − p/x (where p is a positive parameter). The reversion level of this force function is l = p, and the resulting stationary density is Gamma: ϕ_L(x) = c_Lexp ( − x)x^p (x > 0). This Gamma density is unimodal and skewed, and it attains its mode at the reversion level l = p. The mean of this Gamma density is p + 1. Thus, the mean is always greater than the mode—implying that mean-reversion never holds. This example is schematically illustrated in figure 1.

Zoom In Zoom Out Reset image size

Inverse Gamma example. In this example the Langevin dynamics take place on the positive half-line (x > 0). Consider the nonlinear force function F(x) = (p + 1 − 1/x)/x (where p is a positive parameter). The reversion level of this force function is l = 1/(p + 1), and the resulting stationary density is inverse Gamma: ϕ_L(x) = c_Lexp ( − 1/x)/x^{p + 1} (x > 0). This inverse Gamma density is unimodal and skewed, and it attains its mode at the reversion level l = 1/(p + 1). The mean of this inverse Gamma density is infinite in the parameter range p ⩽ 1, and is given by 1/(p − 1) in the parameter range p > 1. Thus, the mean is always greater than the mode—implying that mean-reversion never holds.

Pareto example. In this example the Langevin dynamics take place on the positive half-line (x > 0). Consider the nonlinear force function F(x) = (1 + p)/(1 + x) (where p is a positive parameter). The reversion level of this force function is the origin l = 0, and the resulting stationary density is Pareto: ϕ_L(x) = c_L/(1 + x)^{1 + p} (x > 0). This Pareto density is monotone decreasing, and it attains its mode at the reversion level l = 0. The mean of this Pareto density is infinite in the parameter range p ⩽ 1, and is given by 1/(p − 1) in the parameter range p > 1. Thus, the mean is always greater than the mode—implying that mean-reversion never holds. This example—in the parameter range p > 1—is schematically illustrated in figure 2.

Zoom In Zoom Out Reset image size

We note that the Student example, the inverse Gamma example, and the Pareto example represent scenarios of Langevin dynamics taking place in asymptotically logarithmic potential wells—which are of significant importance in statistical physics [36, 37].

The stochastic dynamics governing the Ornstein–Uhlenbeck process are a sub-class of the more general Langevin dynamics. In turn, the Langevin dynamics are a sub-class of general diffusion dynamics given by the stochastic differential equation

$$\begin{equation} \dot{X}( t) =-F( X( t)) +\sqrt{D( X( t)) }\dot{W}( t). \end{equation} \tag{ 5 }$$

In equation (5) the magnitude of the perturbing noise is state-dependent and is quantified by the diffusion function D(x)—a positive valued and smooth function defined on the real line. Namely, when the process (X(t))_{t ⩾ 0} is at the state x then the magnitude of the perturbing noise is $\sqrt{D( x) }$. The special case of Langevin dynamics is characterized by constant diffusion functions: D(x) ≡ σ².

The predominate and focal role of general diffusion dynamics in continuous-time financial models is eloquently pinpointed in [9]: 'Continuous-time models are widely used to study issues that include the decision to optimally consume, save, and invest, portfolio choice under a variety of constraints, contingent claim pricing, capital accumulation, resource extraction, game theory, and more recently contract theory. Many refinements and extensions are possible, but the basic dynamic model for the variable(s) of interest X(t)is a stochastic differential equation (of the form given by equation (5))'. Equation (5) is indeed the very bedrock of contemporary continuous-time financial models [19, 38–40].

As in the case of the Ornstein–Uhlenbeck process, and as in the case of Langevin dynamics, we consider the force function F(x) to be pushing toward a reversion level l. Namely, we consider the force function F(x) to be negative valued for x < l, and to be positive valued for x > l. The random process (X(t))_{t ⩾ 0} governed by the stochastic differential equation (5) is asymptotically stationary, and it converges in law (as t → ∞) to a stochastic steady state which manifests the 'stochastic balance' between the two opposing drivers—the restoring force and the perturbing white noise. The stationary distribution governing the steady state of the random process (X(t))_{t ⩾ 0} is quantified by the probability density function

$$\begin{equation} \phi _{{\rm D}}( x) =c_{{\rm D}}\frac{1}{D( x) }\exp \bigg( -2\int ^{x}\frac{F( s) }{D( s) }{\rm d}s\bigg) \end{equation} \tag{ 6 }$$

(−∞ < x < ∞; c_D being a normalizing constant). The density ϕ_D(x) is the stationary solution of the Fokker–Planck equation corresponding to the stochastic differential equation (5) [29]. The necessary and sufficient condition required to assure the validity of equation (6) is the integrability of the density ϕ_D(x) over the real line.

A straightforward analysis applied to the stationary density ϕ_D(x) yields the following mode-reversion and mean-reversion conclusions:

• The stationary density ϕ_D(x) is unimodal, and its mode coincides with the reversion level l, if and only if the following condition holds:
  $$\begin{equation} \left\lbrace \begin{array}{@{}ccc@{}}2F( x) +D^{\prime }( x) <0 & {\rm \ \ } & {\rm for }\ x<l, \\ & {\rm \ \ } & \\ 2F( x) +D^{\prime }( x) >0 & {\rm \ \ } & {\rm for }\ x>l. \end{array} \right. \end{equation} \tag{ 7 }$$
• If—in addition to the condition of equation (7)—the stationary density ϕ_D(x) is symmetric around its mode, and possesses a well-defined mean, then the mode and the mean coincide, and the reversion is to the common mode-mean.

Note that in the case of Langevin dynamics D'(x) ≡ 0 and hence the condition of equation (7) is trivially satisfied. In the physical sciences scenarios involving potential functions with multiple minima are prevalent. A potential function V(x) induces the force function F(x) = V'(x), and a natural question arising is: do the minima of the potential function V(x) coincide with the modes of the corresponding stationary densityϕ_D(x)? Consider a potential function V(x) with extrema attained at the points l₁ < l₂ < ⋅⋅⋅ < l_n, where: n is an odd integer, the oddly indexed extremal points are local minima, and the evenly indexed extremal points are local maxima. This implies that the force function F(x) is negative valued on the intervals {( − ∞, l₁), (l₂, l₃), ...(l_{n − 1}, l_n)}, and is positive valued on the intervals {(l₁, l₂), (l₃, l₄), ...(l_n, ∞)}. The shape of the potential function V(x) is reflected in the shape of the stationary density ϕ_D(x) if and only if the extrema of both these functions coincide, and the oddly indexed extremal points are local maxima of ϕ_D(x), and the evenly indexed extremal points are local minima of ϕ_D(x). A straightforward analysis of the stationary density ϕ_D(x) implies that 'shape reflection' holds if and only if the function 2F(x) + D'(x) is negative valued on the intervals {( − ∞, l₁), (l₂, l₃), ...(l_{n − 1}, l_n)}, and is positive valued on the intervals {(l₁, l₂), (l₃, l₄), ...(l_n, ∞)}. This conclusion is the multimodal analogue of the unimodal mode-reversion conclusion stated above. As in the unimodal setting—in the case of Langevin dynamics D'(x) ≡ 0 and hence 'shape reflection' always holds.

In this subsection we consider two transformations of the Ornstein–Uhlenbeck process. These transformations exemplify—even in the context of the mean-reverting Ornstein–Uhlenbeck process—how non-constant diffusion functions naturally arise, and how both mode-reversion and mean-reversion can fail to hold. Throughout this subsection (X(t))_{t ⩾ 0} denotes the Ornstein–Uhlenbeck process presented in the introduction.

The first transformation considers the square displacement of the Ornstein–Uhlenbeck process off its mean, i.e. the process (X₁(t))_{t ⩾ 0} given by X₁(t) = (X(t) − l)². The square-displacement process (X₁(t))_{t ⩾ 0} is non-negative valued. Moreover, Ito's formula [13] implies that the stochastic dynamics of the square-displacement process (X₁(t))_{t ⩾ 0} are governed by the diffusion dynamics of equation (5), with force function F₁(x) = 2rx − σ² (x ⩾ 0), and with diffusion function D₁(x) = 4σ²x (x ⩾ 0). The reversion level of this force function is l₁ = σ²/(2r). Plugging these force and diffusion functions into equation (6) yields the Gamma density

$$\begin{equation} \phi _{{\rm D}}( x) =c_{{\rm D}}\frac{1}{\sqrt{x}}\exp \bigg( - \frac{r}{\sigma ^{2}}x\bigg) \end{equation} \tag{ 8 }$$

(x > 0). This Gamma density is monotone decreasing, and its mode is attained at the origin (yielding an infinite peak). Moreover, the mean of this Gamma density is well-defined and is σ²/(2r). Hence, the reversion level coincides with the mean and is greater than the mode: mode < mean =l₁. We conclude that when passing from the Ornstein–Uhlenbeck process (X(t))_{t ⩾ 0} to the square-displacement process (X₁(t))_{t ⩾ 0} we lose the mode-reversion, but yet we retain the mean-reversion.

The second transformation considers the exponentiation of the Ornstein–Uhlenbeck process, i.e. the process (X₂(t))_{t ⩾ 0} given by X₂(t) = exp (X(t)). Exponentiation is commonplace in settings where the dynamics are multiplicative (rather than additive), and where temporal changes are measured in percentages; such settings are widespread in economics and finance [19, 41], and appear also in the physical sciences—e.g., [42–44]. The geometric Ornstein–Uhlenbeck process (X₂(t))_{t ⩾ 0} is positive valued. Moreover, Ito's formula [13] implies that the stochastic dynamics of the geometric Ornstein–Uhlenbeck process (X₂(t))_{t ⩾ 0} are governed by the diffusion dynamics of equation (5), with force function F₂(x) = x[r(ln (x) − l) − σ²/2] (x > 0), and with diffusion function D₂(x) = σ²x² (x > 0). The reversion level of this force function is l₂ = exp (l + σ²/(2r)). Plugging these force and diffusion functions into equation (6) yields the lognormal density

$$\begin{equation} \phi _{{\rm D}}( x) =c_{{\rm D}}\frac{1}{x}\exp \bigg( -\frac{r }{\sigma ^{2}}( \ln ( x) -l) ^{2}\bigg) \end{equation} \tag{ 9 }$$

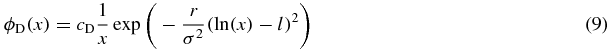
(x > 0). This lognormal density is unimodal and skewed, and it attains its mode at the level exp (l − σ²/(2r)). Moreover, the mean of this lognormal density is well-defined and is exp (l + σ²/(4r)). Hence, the reversion level is greater than the mean, and the mean is greater than the mode: mode < mean<l₂. We conclude that when passing from the Ornstein–Uhlenbeck process (X(t))_{t ⩾ 0} to the geometric Ornstein–Uhlenbeck process (X₂(t))_{t ⩾ 0} we lose both the mode-reversion and the mean-reversion.

The following examples demonstrate the wide range of behaviors that emerge once the diffusion functions are non-constant.

Logistic example. Consider the hyperbolic-sine force function F(x) = (p/2)sinh (x) (where p is a positive parameter), and the hyperbolic-cosine diffusion function D(x) = cosh (x). The reversion level of this force function is the origin l = 0, and the resulting stationary density is logistic: ϕ_D(x) = c_D(cosh (x))^{−p − 1}. This logistic density is unimodal, it attains its mode at the origin, and it is symmetric around its mode. The mean of this logistic density is zero. Thus, the reversion level l coincides with both the mode and the mean, and we have reversion to the common mode-mean. Note that in this example the condition of equation (7) is indeed satisfied.

Student example. Consider the force function $F( x) =x/2 \sqrt{1+x^{2}/p}$, and the diffusion function $D( x) =\sqrt{ 1+x^{2}/p}$ (where p is a positive parameter). The reversion level of this force function is the origin l = 0, and the resulting stationary density is Student: ϕ_D(x) = c_D/(1 + x²/p)^{(1 + p)/2}. This Student density is unimodal, it attains its mode at the origin, and it is symmetric around its mode. The mean of this Student density is ill-defined in the parameter range p ⩽ 1, and is zero in the parameter range p > 1. Thus, the very notion of mean-reversion is well-defined only in the parameter range p > 1; in this parameter range the reversion level l coincides with both the mode and the mean, and we have reversion to the common mode-mean. Note that in this example the condition of equation (7) is indeed satisfied.

Gamma example. In this example the diffusion dynamics take place on the positive half-line (x > 0). Consider the linear force function F(x) = (x − p)/2 (where p is a positive parameter), and the linear diffusion function D(x) = x. The reversion level of this force function is l = p, and the resulting stationary density is Gamma: ϕ_D(x) = c_Dexp ( − x)x^{p − 1} ( x > 0). In the parameter range p ⩽ 1 this Gamma density is monotone decreasing, and its mode is attained at the origin (yielding an infinite peak). In the parameter range p > 1 this Gamma density is unimodal and skewed, and it attains its mode at the level p − 1. The mean of this Gamma density is p. Thus, the reversion level coincides with the mean and is greater than the mode: mode < mean =l. Namely, in this example mean-reversion always holds, whereas mode-reversion never holds. This example—in the parameter range p > 1—is schematically illustrated in figure 3.

Zoom In Zoom Out Reset image size

Inverse Gamma example. In this example the diffusion dynamics take place on the positive half-line (x > 0). Consider the force function F(x) = (p − 1/x)/2 (where p is a positive parameter), and the linear diffusion function D(x) = x. The reversion level of this force function is l = 1/p, and the resulting stationary density is inverse Gamma: ϕ_D(x) = c_Dexp ( − 1/x)/x^{p + 1} (x > 0). This inverse Gamma density is unimodal and skewed, and it attains its mode at the level 1/(p + 1). The mean of this inverse Gamma density is infinite in the parameter range p ⩽ 1, and is given by 1/(p − 1) in the parameter range p > 1. Thus, the reversion level is greater than the mode and is smaller than the mean: mode <l < mean. Namely, in this example neither mode-reversion nor mean-reversion ever hold.

Pareto example. In this example the diffusion dynamics take place on the positive half-line (x > 0). Consider the constant force function F(x) = p/2 (where p is a positive parameter), and the linear diffusion function D(x) = 1 + x. The reversion level of this force function is l = 0, and the resulting stationary density is Pareto: ϕ_D(x) = c_D/(1 + x)^{1 + p} (x > 0). This Pareto density is monotone decreasing, and it attains its mode at the reversion level l = 0. The mean of this Pareto density is infinite in the parameter range p ⩽ 1, and is given by 1/(p − 1) in the parameter range p > 1. Thus, the reversion level coincides with the mode and is smaller than the mean: l =mode < mean. Namely, in this example mode-reversion always holds, whereas mean-reversion never holds. Note that in this example the condition of equation (7) is indeed satisfied. This example—in the parameter range p > 1—is schematically illustrated in figure 4.

Zoom In Zoom Out Reset image size

A class of examples. Consider a diffusion function D(x) which is symmetric around the origin, and a force function given by F(x) = −(p₋/2)D(x) for x < 0, and given by F(x) = (p₊/2)D(x) for x > 0 (where p₋ and p₊ are positive constants). The reversion level of this force function is the origin l = 0, and the resulting stationary density is

$$\begin{equation} \phi _{{\rm D}}( x) =c_{{\rm D}}\frac{1}{D( x) } \cdot \left\lbrace \begin{array}{@{}ccc@{}}\exp ( -p_{-}|x|) & {\rm \ \ } & {\rm for }\ x<0, \\ & {\rm \ \ } & \\ \exp ( -p_{+}|x|) & {\rm \ \ } & {\rm for }\ x>0. \end{array} \right. \end{equation} \tag{ 10 }$$

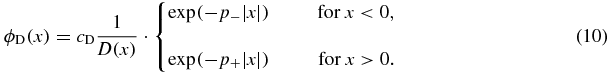
This density is unimodal if and only if the function 1/D(x) is non increasing on the positive half-line (x > 0)—in which case the mode of the density is attained at the origin, and mode-reversion holds. On the other hand, this density is symmetric around the origin if and only if p₋ = p₊—in which case its mean is zero, provided that its mean is indeed well defined. In what follows we show how different choices of the diffusion function D(x), and of the parameters p₋ and p₊, can yield very different examples.

Example I: D(x) = 1/|x|. In this example the density ϕ_D(x) is bi-modal: it has a local maximum at the level −1/p₋, has a global minimum at the origin, and has a local maximum at the level 1/p₊. Moreover, the mean of this density is well-defined. Hence, in this example: (i) the reversion is to the most improbable value of the density; (ii) the notion of mode-reversion is ill-defined—since the density is not unimodal; (iii) mean-reversion holds if and only if p₋ = p₊.

Example II: $D( x) =\exp ( -|x|) \sqrt{|x|}( 1+|x|) )$, and p₋ = p₊ = 1. In this example the density ϕ_D(x) is bi-modal: it attains its global maxima at the levels ±1, and it attains its global minimum at the origin. However, this density has no well-defined mean. Hence, in this example: (i) the reversion is to the most improbable value of the density; (ii) the notion of mode-reversion is ill-defined—since the density is not unimodal; (iii) the notion of mean-reversion is ill-defined—since the density does not have a well-defined mean.

Example III: D(x) = 1/(2 + cos (x)). In this example the density ϕ_D(x) is infinite-modal: it has infinitely many local minima and local maxima, and it attains its global maximum at the origin. Moreover, the mean of this density is well-defined. Hence, in this example: (i) the reversion is to the most probable value of the density; (ii) the notion of mode-reversion is ill-defined—since the density is not unimodal; (iii) mean-reversion holds if and only if p₋ = p₊.

Example IV: D(x) = 1/(sin (x))². In this example the density ϕ_D(x) is infinite-modal: it has infinitely many local maxima, and infinitely many global minima—one of them attained at the origin. Moreover, the mean of this density is well-defined. Hence, in this example: (i) the reversion is to one of the most improbable values of the density; (ii) the notion of mode-reversion is ill-defined—since the density is not unimodal; (iii) mean-reversion holds if and only if p₋ = p₊.