Abstract
Conformal field theory (CFT) has proven to be one of the richest and deepest subjects of modern theoretical and mathematical physics research, especially as regards statistical mechanics and string theory. It has also stimulated an enormous amount of activity in mathematics, shaping and building bridges between seemingly disparate fields through the study of vertex operator algebras, a (partial) axiomatisation of a chiral CFT. One can add to this that the successes of CFT, particularly when applied to statistical lattice models, have also served as an inspiration for mathematicians to develop entirely new fields: the Schramm–Loewner evolution and Smirnov's discrete complex analysis being notable examples.
When the energy operator fails to be diagonalisable on the quantum state space, the CFT is said to be logarithmic. Consequently, a logarithmic CFT is one whose quantum space of states is constructed from a collection of representations which includes reducible but indecomposable ones. This qualifier arises because of the consequence that certain correlation functions will possess logarithmic singularities, something that contrasts with the familiar case of power law singularities. While such logarithmic singularities and reducible representations were noted by Rozansky and Saleur in their study of the U (1|1) Wess–Zumino–Witten model in 1992, the link between the non-diagonalisability of the energy operator and logarithmic singularities in correlators is usually ascribed to Gurarie's 1993 article (his paper also contains the first usage of the term 'logarithmic conformal field theory').
The class of CFTs that were under control at this time was quite small. In particular, an enormous amount of work from the statistical mechanics and string theory communities had produced a fairly detailed understanding of the (so-called) rational CFTs. However, physicists from both camps were well aware that applications from many diverse fields required significantly more complicated non-rational theories. Examples include critical percolation, supersymmetric string backgrounds, disordered electronic systems, sandpile models describing avalanche processes, and so on. In each case, the non-rationality and non-unitarity of the CFT suggested that a more general theoretical framework was needed.
Driven by the desire to better understand these applications, the mid-1990s saw significant theoretical advances aiming to generalise the constructs of rational CFT to a more general class. In 1994, Nahm introduced an algorithm for computing the fusion product of representations which was significantly generalised two years later by Gaberdiel and Kausch who applied it to explicitly construct (chiral) representations upon which the energy operator acts non-diagonalisably. Their work made it clear that underlying the physically relevant correlation functions are classes of reducible but indecomposable representations that can be investigated mathematically to the benefit of applications. In another direction, Flohr had meanwhile initiated the study of modular properties of the characters of logarithmic CFTs, a topic which had already evoked much mathematical interest in the rational case.
Since these seminal theoretical papers appeared, the field has undergone rapid development, both theoretically and with regard to applications. Logarithmic CFTs are now known to describe non-local observables in the scaling limit of critical lattice models, for example percolation and polymers, and are an integral part of our understanding of quantum strings propagating on supermanifolds. They are also believed to arise as duals of three-dimensional chiral gravity models, fill out hidden sectors in non-rational theories with non-compact target spaces, and describe certain transitions in various incarnations of the quantum Hall effect. Other physical applications range from two-dimensional turbulence and non-equilibrium systems to aspects of the AdS/CFT correspondence and describing supersymmetric sigma models beyond the topological sector. We refer the reader to the reviews in this collection for further applications and details.
More recently, our understanding of logarithmic CFT has improved dramatically thanks largely to a better understanding of the underlying mathematical structures. This includes those associated to the vertex operator algebras themselves (representations, characters, modular transformations, fusion, braiding) as well as structures associated with applications to two-dimensional statistical models (diagram algebras, eg. Temperley–Lieb; quantum groups). Not only are we getting to the point where we understand how these structures differ from standard (rational) theories, but we are starting to tackle applications both in the boundary and bulk settings. It is now clear that the logarithmic case is generic, so it is this case that one should expect to encounter in applications. We therefore feel that it is timely to review what has been accomplished in order to disseminate this improved understanding and motivate further applications.
We now give a quick overview of the articles that constitute this special issue.
Adamović and Milas provide a detailed summary of their rigorous results pertaining to logarithmic vertex operator (super)algebras constructed from lattices. This survey discusses the C2-cofiniteness of the (p, p') triplet models (this is the generalisation of rationality to the logarithmic setting), describes Zhu's algebra for (some of) these theories and outlines the difficulties involved in explicitly constructing the modules responsible for their logarithmic nature.
Cardy gives an account of a popular approach to logarithmic theories that regards them, heuristically at least, as limits of ordinary (but non-rational) CFTs. More precisely, it seems that any given correlator may be computed as a limit of standard (non-logarithmic) correlators, any logarithmic singularities that arise do so because of a degeneration when taking the limit. He then illustrates this phenomenon in several theories describing statistical lattice models including the n → 0 limit of the O(n ) model and the Q → 1 limit of the Q-state Potts model.
Creutzig and Ridout review the continuum approach to logarithmic CFT, using the percolation (boundary) CFT to detail the connection between module structure and logarithmic singularities in correlators before describing their proposed solution to the thorny issue of generalising modular data and Verlinde formulae to the logarithmic setting. They illustrate this proposal using the three best-understood examples of logarithmic CFTs: the (1, 2) models, related to symplectic fermions; the 
fractional level WZW model on 
, related to the beta gamma ghosts; and the WZW model on GL(1|1). The analysis in each case requires that the spectrum be continuous; C2-cofinite models are only recovered as orbifolds.
Flohr and Koehn consider the characters of the irreducible modules in the spectrum of a CFT and discuss why these only span a proper subspace of the space of torus vacuum amplitudes in the logarithmic case. This is illustrated explicitly for the (1, 2) triplet model and conclusions are drawn for the action of the modular group. They then note that the irreducible characters of this model also admit fermionic sum forms which seem to fit well into Nahmrsquo;s well-known conjecture for rational theories. Quasi-particle interpretations are also introduced, leading to the conclusion that logarithmic C2-cofinite theories are not so terribly different to rational theories, at least in some respects.
Fuchs, Schweigert and Stigner address the problem of constructing local logarithmic CFTs starting from the chiral theory. They first review the construction of the local theory in the non-logarithmic setting from an angle that will then generalise to logarithmic theories. In particular, they observe that the bulk space can be understood as a certain coend. The authors then show how to carry out the construction of the bulk space in the category of modules over a factorisable ribbon Hopf algebra, which shares many properties with the braided categories arising from logarithmic chiral theories. The authors proceed to construct the analogue of all-genus correlators in their setting and establish invariance under the mapping class group, i.e. locality of the correlators.
Gainutdinov, Jacobsen, Read, Saleur and Vasseur review their approach based on the assumption that certain classes of logarithmic CFTs admit lattice regularisations with local degrees of freedom, for example quantum spin chains (with local interactions). They therefore study the finite-dimensional algebras generated by the hamiltonian densities (typically the Temperley–Lieb algebras and their extensions) that describe the dynamics of these lattice models. The authors then argue that the lattice algebras exhibit, in finite size, mathematical properties that are in correspondence with those of their continuum limits, allowing one to predict continuum structures directly from the lattice. Moreover, the lattice models considered admit quantum group symmetries that play a central role in the algebraic analysis (representation structure and fusion).
Grumiller, Riedler, Rosseel and Zojer review the role that logarithmic CFTs may play in certain versions of the AdS/CFT correspondence, particularly for what is known as topologically massive gravity (TMG). This has been a very active subject over the last five years and the article takes great care to disentangle the contributions from the many groups that have participated. They begin with some general remarks on logarithmic behaviour, much in the spirit of Cardyrsquo;s review, before detailing the distinction between the chiral (no logs) and logarithmic proposals for critical TMG. The latter is then subjected to various consistency checks before discussing evidence for logarithmic behaviour in more general classes of gravity theories including those with boundaries, supersymmetry and galilean relativity.
Gurarie has written an historical overview of his seminal contributions to this field, putting his results (and those of his collaborators) in the context of understanding applications to condensed matter physics. This includes the link between the non-diagonalisability of L0 and logarithmic singularities, a study of the c → 0 catastrophe, and a proposed resolution involving supersymmetric partners for the stress–energy tensor and its logarithmic partner field.
Henkel and Rouhani describe a direction in which logarithmic singularities are observed in correlators of non-relativistic field theories. Their review covers the appropriate modifications of conformal invariance that are appropriate to non-equilibrium statistical mechanics, strongly anisotropic critical points and certain variants of TMG. The main variation away from the standard relativistic idea of conformal invariance is that time is explicitly distinguished from space when considering dilations and this leads to a variety of algebraic structures to explore. In this review, the link between non-diagonalisable representations and logarithmic singularities in correlators is generalised to these algebras, before two applications of the theory are discussed.
Huang and Lepowsky give a non-technical overview of their work on braided tensor structures on suitable categories of representations of vertex operator algebras. They also place their work in historic context and compare it to related approaches. The authors sketch their construction of the so-called P(z)-tensor product of modules of a vertex operator algebra, and the construction of the associativity isomorphisms for this tensor product. They proceed to give a guide to their works leading to the first authorrsquo;s proof of modularity for a class of vertex operator algebras, and to their works, joint with Zhang, on logarithmic intertwining operators and the resulting tensor product theory.
Morin-Duchesne and Saint-Aubin have contributed a research article describing their recent characterisation of when the transfer matrix of a periodic loop model fails to be diagonalisable. This generalises their recent result for non-periodic loop models and provides rigorous methods to justify what has often been assumed in the lattice approach to logarithmic CFT. The philosophy here is one of analysing lattice models with finite size, aiming to demonstrate that non-diagonalisability survives the scaling limit. This is extremely difficult in general (see also the review by Gainutdinov et al ), so it is remarkable that it is even possible to demonstrate this at any level of generality.
Quella and Schomerus have prepared an extensive review covering their longstanding collaboration on the logarithmic nature of conformal sigma models on Lie supergroups and their cosets with applications to string theory and AdS/CFT. Beginning with a very welcome overview of Lie superalgebras and their representations, harmonic analysis and cohomological reduction, they then apply these mathematical tools to WZW models on type I Lie supergroups and their homogeneous subspaces. Along the way, deformations are discussed and potential dualities in the corresponding string theories are described.
Ruelle provides an exhaustive account of his substantial contributions to the study of the abelian sandpile model. This is a statistical model which has the surprising feature that many correlation functions can be computed exactly, in the bulk and on the boundary, even though the spectrum of conformal weights is largely unknown. Nevertheless, there is much evidence suggesting that its scaling limit is described by an, as yet unknown, c = −2 logarithmic CFT.
Semikhatov and Tipunin present their very recent results regarding the construction of logarithmic chiral W-algebra extensions of a fractional level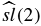 
algebra. The idea is that these algebras are the centralisers of a rank-two Nichols algebra which possesses at least one fermionic generator. In turn, these Nichols algebra generators are represented by screening operators which naturally appear in CFT bosonisation. The major advantage of using these generators is that they give strong hints about the representation theory and fusion rules of the chiral algebra.
Simmons has contributed an article describing the calculation of various correlation functions in the logarithmic CFT that describes critical percolation. These calculations are interpreted geometrically in a manner that should be familiar to mathematicians studying Schramm–Loewner evolutions and point towards a (largely unexplored) bridge connecting logarithmic CFT with this branch of mathematics.
Of course, the field of logarithmic CFT has benefited greatly from the work of many of researchers who are not represented in this special issue. The interested reader will find many links to their work in the bibliographies of the special issue articles and reviews.
In summary, logarithmic CFT describes an extension of the incredibly successful methods of rational CFT to a more general setting. This extension is necessary to properly describe many different fundamental phenomena of physical interest. The formalism is moreover highly non-trivial from a mathematical point of view and so logarithmic theories are of significant interest to both physicists and mathematicians. We hope that the collection of articles that follows will serve as an inspiration, and a valuable resource, for both of these communities.