Abstract
Vortices in the solar photosphere can be linked to a wide range of events, such as small-scale solar eruptions, wave excitation, and heating of the upper part of the solar atmosphere. Despite their importance in solar physics, most of the current studies on photospheric vortices are based on methods that are not invariant under time-dependent translations and rotations of the reference frame and are Eulerian; i.e., they are based on single snapshots of a velocity field and, therefore, do not convey information on the true long-term motion of fluid particles on a time-varying field. Another issue with methods for vortex detection is that typically they provide false identifications in highly compressible flows. This Letter presents a novel criterion that effectively removes wrong detections based on the geometry of the streamlines of the displacement vector of fluid elements and can be readily applied to other astrophysical flows. The new criterion is applied to the Lagrangian-averaged vorticity deviation (LAVD), which is a recently developed frame invariant vortex detection method. The advantage of LAVD is that it delimits the vortices' outer boundaries precisely by following up the trajectories of fluid elements in space and time. The proposed method is compared with two other techniques using horizontal velocity fields extracted from Hinode satellite data.
Export citation and abstract BibTeX RIS
1. Introduction
The turbulent flows observed in the photosphere influence the conditions found in the upper solar atmosphere as they transport and compress the magnetic field lines. One of the remarkable features of these turbulent flows is the presence of vortical motions in different scales. They were first detected by Brandt et al. (1988) after Nordlund (1985) showed from simulations that strong downflow regions tend to display swirling motions. The photospheric vortices can twist magnetic field lines and mix their polarities, leading to small-scale eruptions (Kitiashvili et al. 2013) and solar magnetic tornadoes (Su et al. 2012; Wedemeyer-Böhm et al. 2012; Wedemeyer & Steiner 2014). The vortices in strongly magnetized intergranular lanes may also be linked with more intense pointing flux (Shelyag et al. 2012), which could explain energy transport to the upper atmosphere. Another way vortices may influence the energy transport is by triggering magnetohydrodynamic (MHD) waves that could channel the necessary amount of energy to both chromosphere and corona (Murawski et al. 2018). Therefore, investigating the evolution of photospheric vortices is a crucial step toward the understanding of nanoflare dynamics and energy transport from the photosphere to the corona.
Most of the existing observational studies of vortices are based on following up passively advected tracers in the flow (Attie et al. 2009; Bonet et al. 2010) or on visual inspection of the motion of magnetic structures (Bonet et al. 2008; Balmaceda et al. 2010) to check for swirling patterns. There are also more automated methods, such as vorticity strength (VS; Zhou et al. 1999) and Γ detection (Graftieaux et al. 2001), which recently have been applied to detect photospheric vortices (Moll et al. 2012; Giagkiozis et al. 2017; Kato & Wedemeyer 2017). The VS method identifies only vortex regions without giving precise information on their boundaries, which should be inferred based on user-defined thresholds or some other technique. Γ detection computes the vortex boundary, but the method is based on the topology of the streamlines of the velocity field, which is not an objective quantity; i.e., it is not invariant under time-dependent rotations and translations of the observer. Most of the existing methods for defining vortices may not be valid if an accelerated frame is used. This may pose a problem when following up the vortices and finding information on their dynamics, because what is perceived as a vortex by an observer may not be seen as such by another observer in a different frame. For further discussions on the importance of objectivity in the detection of coherent structures in fluids, see, e.g., Peacock et al. (2015) and Haller et al. (2016).
None of the methods employed to identify vortices in the photosphere so far can precisely objectively identify vortex boundaries. Furthermore, the aforementioned techniques are Eulerian, being based on single snapshots of the velocity field and not taking into account the dynamics of fluid particles in a time-varying field, where a given vortex may be short-lived and have a small impact on the long-term behavior of particles. In this Letter we introduce the Lagrangian Averaged Vorticity Deviation (LAVD) technique, developed by Haller et al. (2016) to identify objective Lagrangian vortex boundaries; it has been successfully employed in vortex detection in 3D numerical simulations of an MHD dynamo (Rempel et al. 2017). We present state-of-the-art vortex detection in the photosphere, comparing the VS, Γ, and LAVD methods. Although all of the techniques have their strengths and weaknesses, we verify that some false detections are found, in the sense that the resulting vortical structures do not generate true swirling patterns in the fluid pathlines. Thus, we introduce a new parameter d to dismiss false vortex detections based on the streamlines of the displacement vector. By combining LAVD with d, we propose a robust objective Lagrangian method to detect photospheric vortices.
2. Data and Methodology
The velocity field used in our analysis was obtained by applying local correlation track (LCT) to the series of intensity maps from the quiet-Sun disk center. The intensity maps were constructed using Stokes I and V images from the Narrowband Filter Imager on board Hinode on 2010 November 2–3. The cadence of observations is 90 s and the total time of uninterrupted observation is 24 hr. The spatial resolution is around 0 32. More information on the data and the employed LCT parameters can be found in Gošić et al. (2014) and Requerey et al. (2018), respectively. Figure 1 displays the area of the selected quiet-Sun region, on a single supergranulation cell of about 50 Mm × 50 Mm, colored by the intensity of the horizontal velocity vectors at t = 05:47:34 UT. This quiet-Sun region presents coherent vortex flows with lifetimes ranging from a couple of minutes to around 5 hr.
32. More information on the data and the employed LCT parameters can be found in Gošić et al. (2014) and Requerey et al. (2018), respectively. Figure 1 displays the area of the selected quiet-Sun region, on a single supergranulation cell of about 50 Mm × 50 Mm, colored by the intensity of the horizontal velocity vectors at t = 05:47:34 UT. This quiet-Sun region presents coherent vortex flows with lifetimes ranging from a couple of minutes to around 5 hr.
Figure 1. Horizontal component of the photospheric velocity field on a single supergranulation cell of about 50 Mm × 50 Mm for a quiet-Sun region at disk center for t = 05:47:34 UT on 2010 November 2.
Download figure:
Standard image High-resolution imageThe identification of a vortex is intrinsically related to its definition. In the literature of fluid dynamics, there is a general agreement that vortices are related to high-vorticity regions in the flow (Haller 2005). However, that condition is not sufficient to define a vortex, as intense vorticity may not be associated with swirling motions, but with vigorous shear instead. To avoid detecting the shearing and non-swirling flows, both the VS and Γ methods provide ways to identify regions where the vorticity is higher than the strain. The VS method identifies eddies structures based on an analysis of the eigenvalues of the velocity gradient tensor 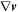 . Kato & Wedemeyer (2017) developed an algorithm where first the VS field is obtained as the imaginary part of all eigenvalues in the flow plane. Next, they consider the local maxima of this VS field as vortex candidates; a vortex is determined approximately as a circle whose area is equivalent to the area enclosed by a contour line for intensity values larger than 10% of the intensity peak value. We call the new methodology developed by Kato & Wedemeyer (2017) vorticity strength and convexity (VSC).
. Kato & Wedemeyer (2017) developed an algorithm where first the VS field is obtained as the imaginary part of all eigenvalues in the flow plane. Next, they consider the local maxima of this VS field as vortex candidates; a vortex is determined approximately as a circle whose area is equivalent to the area enclosed by a contour line for intensity values larger than 10% of the intensity peak value. We call the new methodology developed by Kato & Wedemeyer (2017) vorticity strength and convexity (VSC).
The Γ method is able to determine both the vortex boundary and its center by means of two scalar quantities, Γ1 and Γ2, computed at each point P in a plane. For each possible contour S around P, the scalars are calculated as
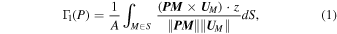
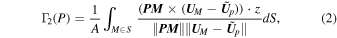
where PM denotes the displacement vector from point P to a point M in S, UM and Up denote the velocity vectors at M and P, respectively, z is a unit vector normal to the plane, A is the area of S, and 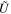 is the mean velocity vector in region S. Γ1 is used to detect vortex cores, because in the center of an axisymmetrical vortex its value reaches unity. Graftieaux et al. (2001) established the contour of a vortex as the outer boundary of the region surrounding a vortex core where rotation dominates over strain. For an incompressible velocity field, that would be the contour of the regions where
is the mean velocity vector in region S. Γ1 is used to detect vortex cores, because in the center of an axisymmetrical vortex its value reaches unity. Graftieaux et al. (2001) established the contour of a vortex as the outer boundary of the region surrounding a vortex core where rotation dominates over strain. For an incompressible velocity field, that would be the contour of the regions where 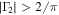 .
.
The VSC and Γ2 methods are Galilean invariant, but they have never been shown to be objective. Haller et al. (2016) developed a technique to define coherent vortices objectively by using the LAVD
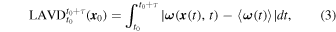
where 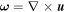 is the vorticity, τ is a given time interval, and
is the vorticity, τ is a given time interval, and  denotes the instantaneous spatial mean. The fluid particle positions are obtained as solutions of the equation
denotes the instantaneous spatial mean. The fluid particle positions are obtained as solutions of the equation 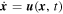 with the initial condition
with the initial condition 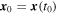 . The candidates for vortex centers are found as points of local maxima of the LAVD field. Haller et al. (2016) demonstrated that the spin tensor and the vorticity are not objective quantities, whereas the averaged vorticity deviation (the integrand in Equation (3)) is an objective quantity. Besides being frame invariant, another advantage of the LAVD method compared to an Eulerian vortex detection is that it actually identifies the vortices persisting in the flow, and not only an instantaneous swirl-like structure that may not last and therefore have low impact in the plasma flow dynamics.
. The candidates for vortex centers are found as points of local maxima of the LAVD field. Haller et al. (2016) demonstrated that the spin tensor and the vorticity are not objective quantities, whereas the averaged vorticity deviation (the integrand in Equation (3)) is an objective quantity. Besides being frame invariant, another advantage of the LAVD method compared to an Eulerian vortex detection is that it actually identifies the vortices persisting in the flow, and not only an instantaneous swirl-like structure that may not last and therefore have low impact in the plasma flow dynamics.
3. Results
The methods for vortex detection described in the previous section consider that the vortex candidates are regions with significant vorticity. As mentioned before, a region with high vorticity does not necessarily imply a vortex. Both LAVD and VSC try to dismiss the wrong vortex candidates by applying a condition of high convexity to the vortex boundaries. For LAVD, the boundaries are obtained as the outermost convex closed contour lines surrounding points of local LAVD maxima. For VSC, Kato & Wedemeyer (2017) tried to fit a circle inside a closed contour line around the local maxima of the VS field. Instead of a circle, we consider the more general condition used for LAVD; i.e., that the outermost convex closed contour line around the local maxima of VS provides a vortex boundary. A certain deviation from convexity is acceptable, being measured by the convexity deficiency, c, defined as the ratio of the area difference between the curve and its convex hull to the area enclosed by the curve (Haller et al. 2016).
To illustrate some of the problems found in vortex detection, Figure 2 shows the boundary of structures identified as vortices by the VSC (Figures 2(a) and (b)) and LAVD (Figures 2(c) and (d)) methods using different values for the convex deficiency, c. For the VSC method the contours were obtained for t0 = 05:47:34 UT, and for LAVD the contours were obtained by integrating from t0 = 05:47:34 UT to t1 = 06:02:34 UT. We have selected a time interval of 15 minutes, which is around twice the mean duration of vortices in the photosphere of a quiet Sun (Bonet et al. 2010). The streamlines in Figure 2 are for the fluid displacement vector field 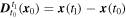 , where
, where 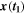 is obtained by integrating
is obtained by integrating 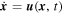 from t = t0 to t = t1 with
from t = t0 to t = t1 with 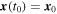 as initial condition. Because VSC is an Eulerian operator, we want to know the displacement field for a short time interval, then, in Figures 2(a) and (b),
as initial condition. Because VSC is an Eulerian operator, we want to know the displacement field for a short time interval, then, in Figures 2(a) and (b), 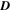 is computed for t0 = 05:47:34 UT and t1 = 05:49:04 UT. In the case of LAVD, (Figures 2(c) and (d))
is computed for t0 = 05:47:34 UT and t1 = 05:49:04 UT. In the case of LAVD, (Figures 2(c) and (d)) 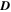 is computed for t0 = 05:47:34 UT and t1 = 06:02:34 UT. In Figures 2(a) and (c) it can be seen that a shear region is wrongly detected as a vortex by both operators, even when a low convexity deficiency (c = 0.00001) is used. As a matter of fact, our experience reveals that the value of c should not be too small because the highly compressible solar plasma often displays vortical regions with a strong departure from convexity. For instance, in Figure 2(b) the streamlines show a clearly vortical structure, but VSC missed the vortex center for c = 0.00001, whereas the vortex was correctly identified for c = 0.07. In other words, dismissing detections by requiring that the structure should have a low convexity deficiency may not only result in false detections, but also fail to detect some true vortices. Therefore, some other criterion is needed to filter vortex detection in photospheric plasma flows. As for the Γ method, it corrects the false identifications by using the parameter Γ1, which analyses the geometry of the velocity streamlines. Thus, from all the vortex boundary candidates identified in the velocity flow by Γ2, we are left with the contours that encompass a point where the velocity streamlines obey the Γ1 criterion.
is computed for t0 = 05:47:34 UT and t1 = 06:02:34 UT. In Figures 2(a) and (c) it can be seen that a shear region is wrongly detected as a vortex by both operators, even when a low convexity deficiency (c = 0.00001) is used. As a matter of fact, our experience reveals that the value of c should not be too small because the highly compressible solar plasma often displays vortical regions with a strong departure from convexity. For instance, in Figure 2(b) the streamlines show a clearly vortical structure, but VSC missed the vortex center for c = 0.00001, whereas the vortex was correctly identified for c = 0.07. In other words, dismissing detections by requiring that the structure should have a low convexity deficiency may not only result in false detections, but also fail to detect some true vortices. Therefore, some other criterion is needed to filter vortex detection in photospheric plasma flows. As for the Γ method, it corrects the false identifications by using the parameter Γ1, which analyses the geometry of the velocity streamlines. Thus, from all the vortex boundary candidates identified in the velocity flow by Γ2, we are left with the contours that encompass a point where the velocity streamlines obey the Γ1 criterion.
Figure 2. False (left panel) and true (right panel) vortex detections by VSC (at t = 05:47:34 UT) and LAVD (ti = 05:47:34 UT and tf = 06:02:34 UT) methods with different convex deficiency (c) parameters. The streamlines in VSC (LAVD) detections are for the fluid displacement, 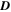 , from t0 = 05:47:34 UT to t1 = 05:49:04 UT (t1 = 06:02:34 UT). (a), (b) VSC detection for c = 0.07 (red lines) and c = 0.00001 (light blue lines). (c), (d) LAVD detection for c = 0.07 (orange lines) and 0.00001 (petrol blue lines).
, from t0 = 05:47:34 UT to t1 = 05:49:04 UT (t1 = 06:02:34 UT). (a), (b) VSC detection for c = 0.07 (red lines) and c = 0.00001 (light blue lines). (c), (d) LAVD detection for c = 0.07 (orange lines) and 0.00001 (petrol blue lines).
Download figure:
Standard image High-resolution image3.1. Lagrangian Vortex Detection
The validation by the Γ1 parameter relies on a vortex definition based on the geometry of the instantaneous streamlines. Such a definition is stated by Robinson (1991, p. 614)
"A vortex exists when instantaneous streamlines mapped onto a plane normal to the vortex core exhibit a roughly circular or spiral pattern when viewed from a reference frame moving with the center of the vortex core."
While the definition above is intuitive, an instantaneous description of the velocity field may not reflect the path followed by the fluid elements as the velocity field evolves in time. Therefore, we suggest a new method to correct false vortex detections based on the geometry of the streamlines of the displacement field  .
.
To check whether a structure detected by LAVD or VSC is a true vortex, we perform the geometric verification of the streamlines of the displacement vector. This is done by checking the displacement of particles that are initially placed at each grid point and then advected by the velocity flows during the selected time interval. In a cartesian grid, a particle at point (i, j) is considered a vortex center if the x and y-components of the displacement vectors (Dx, Dy) of the particles at the four nearest neighboring points, (i, j + 1), (i − 1, j), (i, j − 1), (i + 1, j), obey the following conditions for a clockwise vortex (counter-clockwise vortex),
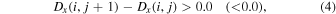
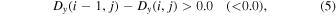
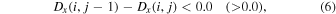

We call the conditions on Equations (4)–(7) the d criterion and they are illustrated in Figure 3 for a counter-clockwise vortex.
Figure 3. Neighboring points and their displacements around the grid point (i, j).
Download figure:
Standard image High-resolution imageFigure 4 displays the results obtained by applying the VSC, LAVD, and Γ methods to the velocity field of our quiet-Sun region. Figures 4(a) and (c) show the original detection with c = 0.07 for VSC (at t0 = 05:47:34 UT) and LAVD (t0 = 05:47:34 and t1 = 06:02:34 UT) with the horizontal displacement vector, 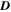 . We have relaxed the convexity parameter as we verified that the use of smaller c values only results in the loss of some real vortices. For the validation of the VSC (LAVD) detection we use the d-parameter, considering the displacement of fluid elements from t0 = 05:47:34 UT to t1 = 05:49:04 UT (t1 = 06:02:34 UT). The points that are in accordance with the d-parameter are shown as blue points in Figures 4(a)–(d). Figures 4(b), (d) are colored by
. We have relaxed the convexity parameter as we verified that the use of smaller c values only results in the loss of some real vortices. For the validation of the VSC (LAVD) detection we use the d-parameter, considering the displacement of fluid elements from t0 = 05:47:34 UT to t1 = 05:49:04 UT (t1 = 06:02:34 UT). The points that are in accordance with the d-parameter are shown as blue points in Figures 4(a)–(d). Figures 4(b), (d) are colored by 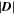 and shows the contours detected by VSC (LAVD), where at least one grid point obeys the d-parameter. The results for the Γ2 and Γ1 at t = 05:47:34 UT are given in Figures 4(e) and (f). All of the potential vortex contours obtained for
and shows the contours detected by VSC (LAVD), where at least one grid point obeys the d-parameter. The results for the Γ2 and Γ1 at t = 05:47:34 UT are given in Figures 4(e) and (f). All of the potential vortex contours obtained for 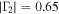 are shown in Figure 4(e) colored in green, together with the points that obey the criterion
are shown in Figure 4(e) colored in green, together with the points that obey the criterion 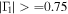 , denoted by black circles. We have selected a lower value for
, denoted by black circles. We have selected a lower value for 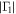 due to the non-axisymmetric nature of vortices in the photosphere. Figure 4(f) shows the Γ detection with the plane color-coded by the intensity of horizontal velocities in the photosphere.
due to the non-axisymmetric nature of vortices in the photosphere. Figure 4(f) shows the Γ detection with the plane color-coded by the intensity of horizontal velocities in the photosphere.
Figure 4. Vortex detection by the normal and corrected Eulerian and Lagrangian methods. (a) Structures (red) and the displacement vector field,  , detected by the normal VSC method (at t0 = 05:47:34 UT) for c = 0.07 and the points (blue) obeying the d criterion. (b) Vortex detection by the corrected VSC+d method (from t0 = 05:47:34 UT to t1 = 05:49:04 UT), colored in red, and the horizontal plane colored by
, detected by the normal VSC method (at t0 = 05:47:34 UT) for c = 0.07 and the points (blue) obeying the d criterion. (b) Vortex detection by the corrected VSC+d method (from t0 = 05:47:34 UT to t1 = 05:49:04 UT), colored in red, and the horizontal plane colored by 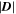 . (c) Structures (orange) and the displacement vector field detected by the normal LAVD method (from t0 = 05:47:34 UT to t1 = 06:02:34 UT) for c = 0.07 and the points (blue) obeying the d criterion. (d) Vortex detection by the corrected LAVD+d method, colored in orange, and the horizontal plane colored by
. (c) Structures (orange) and the displacement vector field detected by the normal LAVD method (from t0 = 05:47:34 UT to t1 = 06:02:34 UT) for c = 0.07 and the points (blue) obeying the d criterion. (d) Vortex detection by the corrected LAVD+d method, colored in orange, and the horizontal plane colored by  . (e) Structures detected by Γ2 are shown by the green contours and the velocity field vectors (dark gray) at t0 = 05:47:34 UT. (f) Vortex detection by the Γ method (green contours) after the selection by the Γ1 criterion; the horizontal plane is colored by the magnitude of the horizontal velocity field.
. (e) Structures detected by Γ2 are shown by the green contours and the velocity field vectors (dark gray) at t0 = 05:47:34 UT. (f) Vortex detection by the Γ method (green contours) after the selection by the Γ1 criterion; the horizontal plane is colored by the magnitude of the horizontal velocity field.
Download figure:
Standard image High-resolution imageThe accuracy of both the d and Γ1 criteria can be checked in Figure 5, which shows a closer view of some of the vortices detected in Figure 4. For the VSC and LAVD methods, Figures 5(a)–(f), the planes are colored by 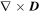 and the black streamlines are for the displacement field. For the LAVD method, we only display structures that were not detected by the Eulerian methods (vortices labeled as B3, B6, and B7 in Figure 4(d)). We confirm that the d-parameter has properly identified the correct vortices among both LAVD and VSC detections as the displacement streamlines show swirling patterns. For the Γ method (Figures 5(g)–(i)) the panels are colored by
and the black streamlines are for the displacement field. For the LAVD method, we only display structures that were not detected by the Eulerian methods (vortices labeled as B3, B6, and B7 in Figure 4(d)). We confirm that the d-parameter has properly identified the correct vortices among both LAVD and VSC detections as the displacement streamlines show swirling patterns. For the Γ method (Figures 5(g)–(i)) the panels are colored by 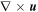 and the dark gray streamlines are for the velocity field.
and the dark gray streamlines are for the velocity field.
Figure 5. Enlargement of the vortex regions detected by VSC, LAVD, and Γ methods. (a), (b), and (c) refer to detections labeled A1, A3, and A4 in Figure 4(b), respectively. (d), (e), and (f) refer to detections labeled B3, B6, and B7 in Figure 4(d), respectively. (g), (h), and (i) refer to detections labeled C1, C2, and C3 in Figure 4(f).
Download figure:
Standard image High-resolution imageThe VSC + d-parameter identified four vortices and the Γ method detected a total of three structures in the quiet-Sun region for t0 = 05:47:34 UT. The vortices labeled as A3 and A4 were not detected by Γ. The A3 vortex was missed by Γ1 which means that the velocity streamlines were not spiraling at the time of the detection. As for the A4 vortex, it did not obey the Γ2 criterion on comparing vorticity and strain in the region. Both Γ and VSC detected the A1/C1 and A2/C2 vortices in Figures 4(b) and (f), but VSC was not able to detect C3. Therefore, the two Eulerian methods do not agree in all detections and also present differences in the vortex shapes. Additionally, there seems to be no clear correlation between the streamlines around the vortex centers and the detected outer boundaries.
Except for C3, the LAVD method detected the same vortices identified by the Eulerian techniques (structures labeled by B1, B2, B4, B5) and also three other vortices labeled as B3, B6, and B7 in Figures 5(d) and (f). Vortex C3 was missed by the Lagrangian method because it is short-lived, having a small impact on the particles' dynamics in the time interval considered. There are also considerable differences between the area of the vortices that were detected by all three methods applied in this Letter. Also, from the plots in Figures 5(d)–(f) it is possible to see that LAVD can delimit the region where the rotation imposed by a vortex more strongly affects the particles' displacements because each vortex boundary closely surrounds an area with strong 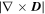 .
.
4. Discussions and Conclusions
The three scalar quantities tested in this Letter, VSC, Γ2, and LAVD, were shown to be prone to false vortex detection when used in our photospheric horizontal velocity fields. This may be due to the highly compressible 3D nature of the plasma, as well as the fact that the velocity vectors are tiny in comparison with the length scales of the quiet-Sun region, which may hinder the accurate numerical computation of fluid trajectories, especially relevant in the LAVD method. Therefore, it is necessary to employ an additional procedure to filter the initial detection. In the Γ method, the Γ1 criterion corrects the wrong detections of Γ2. Although it is necessary to relax the Γ1 values for flows in the photosphere, the final identifications were in general correct, but some true vortices were missed. Nonetheless, the computation of Γ1 is done from a non-objective quantity, the velocity streamlines, which poses a conceptual problem as the detection will depend on the reference frame adopted. To provide a filter for vortex detection for an objective quantity like LAVD, we have introduced the d-parameter. The d-parameter was able to correctly select the true vortices in the regions detected by LAVD, being also effective concerning the regions detected by VSC.
The number of vortices and their shapes as obtained by LAVD+d is usually different from the ones obtained with the Eulerian techniques of VSC and Γ. This is so because the Lagrangian techniques are computed over a given time interval, when new vortices that are not present in the initial snapshot may arise. The LAVD field will provide information on the main coherent structures in the given time interval; that is, the ones with stronger influence over neighboring fluid particles. These are precisely the regions where a stronger convergence of magnetic field lines should take place.
In conclusion, the LAVD method coupled with the d-parameter provides a novel and effective way of detecting objective vortices in the solar photosphere and other astrophysical applications. A series of computations using VSC, Γ, and LAVD in different instances of photospheric velocity fields confirm the results of the present Letter and should appear in a future work.
This work was supported by CAPES, process 88887.137510/2017-00. E.L.R. acknowledges FAPESP 2013/26258-4.









