Abstract
In the Conventional Theory (CT) of the electron broadening of hydrogenlike spectral lines in plasmas, the perturbing electrons are considered moving along hyperbolic trajectories in the Coulomb field of the effective charge Z − 1 (in atomic units), where Z is the nuclear charge of the radiating ion. Thus, the CT assumed that the motion of the perturbing electron can be described in frames of a two-body problem, one particle being the perturbing electron and the other 'particle' being the charge Z − 1. However, in reality it is a three-body problem, involving the perturbing electron, the nucleus, and the bound electron, so that trajectories of the perturbing electrons should be more complicated. In the present paper we take this into account via the standard analytical method of separating rapid and slow subsystems by using the fact that the characteristic frequency of the motion of the bound electron around the nucleus is much higher than the characteristic frequency of the motion of the perturbing electron around the radiating ion. By applying this method we obtain more accurate analytical results for the electron broadening operator than in the CT. We show by examples of the electron broadening of the Lyman lines of He II that the allowance for this effect increases with the electron density Ne, becomes significant already at Ne ∼ 1017 cm−3 and very significant at higher densities. We also briefly discuss a paper by Baryshnikov and Lisitsa (Sov. Phys. JETP 53 (1981) 471) where the fundamental symmetry of the effective potential for this problem was used in a different way.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The theory of the Stark broadening of hydrogenlike spectral lines by plasma electrons, developed by Griem and Shen [1] and later presented also in books [2, 3], is usually referred to as the Conventional Theory, hereafter CT, also known as the standard theory. (Further advances in the theory of the Stark broadening of hydrogenlike spectral lines by plasma electrons can be found, e.g., in books [4, 5] and references therein.) In the CT, the perturbing electrons are considered moving along hyperbolic trajectories in the Coulomb field of the effective charge Z − 1 (in atomic units), where Z is the nuclear charge of the radiating ion. In other words, in the CT there was made a simplifying assumption that the motion of the perturbing electron can be described in frames of a two-body problem, one particle being the perturbing electron and the other 'particle' being the charge Z − 1.
However, in reality one have to deal with a three-body problem: the perturbing electron, the nucleus, and the bound electron. Therefore, trajectories of the perturbing electrons should be more complicated.
In the present paper we take this into account by using the standard analytical method of separating rapid and slow subsystems—see, e.g., book [6]. The characteristic frequency of the motion of the bound electron around the nucleus is much higher than the characteristic frequency of the motion of the perturbing electron around the radiating ion. Therefore the former represents the rapid subsystem and the latter represents the slow subsystem. This approximate analytical method allows a sufficiently accurate treatment in situations where the perturbation theory fails—see, e.g., book [6].
By applying this method we obtain more accurate analytical results for the electron broadening operator than in the CT. We show by examples of the electron broadening of the Lyman lines of He II that the allowance for this effect increases with the electron density Ne, becomes significant already at Ne ∼ 1017 cm−3 and very significant at higher densities.
2. Analytical results
In the CT the electron broadening operator is expressed in the form (see, e.g., paper [1])
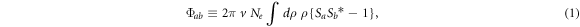
where Ne, 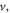 and
and  are the electron density, velocity, and impact parameter, respectively;
are the electron density, velocity, and impact parameter, respectively; 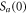 and
and  are the S matrices for the upper (a) and lower (b) states involved in the radiative transition, respectively; {...} stands for the averaging over angular variables of vectors v and ρ. Further in the CT, the collisions are subdivided into weak and strong. The weak collisions are treated by the time-dependent perturbation theory. The impact parameter, at which the formally calculated expression {SaSb* − 1} for a weak collision starts violating the unitarity of the S-matrices, serves as the boundary between the weak and strong collisions and is called Weisskopf radius ρWe.
are the S matrices for the upper (a) and lower (b) states involved in the radiative transition, respectively; {...} stands for the averaging over angular variables of vectors v and ρ. Further in the CT, the collisions are subdivided into weak and strong. The weak collisions are treated by the time-dependent perturbation theory. The impact parameter, at which the formally calculated expression {SaSb* − 1} for a weak collision starts violating the unitarity of the S-matrices, serves as the boundary between the weak and strong collisions and is called Weisskopf radius ρWe.
So, in the CT the integral over the impact parameter diverges at small ρ. Therefore in the CT this integral is broken down in two parts: from 0 to ρWe (strong collisions) and from ρWe to ρmax for weak collisions. The upper cutoff ρmax (typically chosen to be the Debye radius ρD = [T/(4πe2Ne)]1/2, where T is the electron temperature) is necessary because this integral diverges also at large ρ.
In the CT, after calculating the S matrices for weak collisions, the electron broadening operator becomes (in atomic units)

where 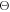 is the scattering angle for the collision between the perturbing electron and the radiating ion (the dependence between
is the scattering angle for the collision between the perturbing electron and the radiating ion (the dependence between 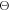 and ρ being discussed below) and the plasma electron and the operator
and ρ being discussed below) and the plasma electron and the operator 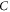 is
is
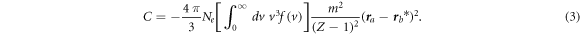
Here f(v) is the velocity distribution of the perturbing electrons, 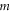 is the reduced mass of the system 'perturbing electron—radiating ion'; r is the radius-vector operator of the bound electron (which scales with Z as 1/Z), its subscripts a or b correspond to this operator acting on the upper or lower states, respectively, involved in the radiative transition. The expression (ra−rb*)2 stands for the scalar product (also known as the dot-product) of the operator (ra−rb*) with itself. In the theory of the dynamical Stark broadening of spectral lines in plasmas by electrons, the corresponding matrix elements are calculated with respect to the unperturbed wave functions.
is the reduced mass of the system 'perturbing electron—radiating ion'; r is the radius-vector operator of the bound electron (which scales with Z as 1/Z), its subscripts a or b correspond to this operator acting on the upper or lower states, respectively, involved in the radiative transition. The expression (ra−rb*)2 stands for the scalar product (also known as the dot-product) of the operator (ra−rb*) with itself. In the theory of the dynamical Stark broadening of spectral lines in plasmas by electrons, the corresponding matrix elements are calculated with respect to the unperturbed wave functions.
In the CT the scattering occurs in the effective Coulomb potential, so that the trajectory of the perturbing electron is hyperbolic and the relation between the impact parameter and the scattering angle is given by
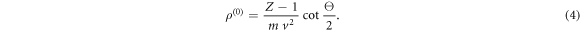
Here the superscript (0) in 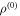 refers to hyperbolic trajectories.
refers to hyperbolic trajectories.
In the present paper we consider the realistic situation where trajectories of the perturbing electrons are more complicated because the perturbing electron, the nucleus, and the bound electron should be more accurately treated as the three-body problem. We use the standard analytical method of separating rapid and slow subsystems—see, e.g., book [6]. It is applicable here because the characteristic frequency vTe/ρWe of the variation the electric field of the perturbing electrons at the location of the radiating ion is much smaller than the frequency Ωab of the spectral line (the latter, e.g., in case of the radiative transition between the Rydberg states would be the Keppler frequency or its harmonics)—more details are presented in appendix.
The first step in this method is to 'freeze' the slow subsystem (perturbing electron) and to find the analytical solution for the energy of the rapid subsystem (the radiating ion) that would depend on the frozen coordinates of the slow subsystem (in our case it will be the dependence on the distance R of the perturbing electron from the radiating ion). To the first non-vanishing order of the R-dependence, the corresponding energy in the parabolic quantization is given by
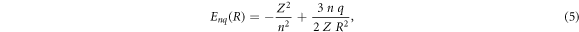
where 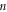 and
and 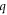 = n1−n2 are the principal and electric quantum numbers, respectively, of the Stark state of the radiating ion; n1 and n2 are the parabolic quantum numbers of that state.
= n1−n2 are the principal and electric quantum numbers, respectively, of the Stark state of the radiating ion; n1 and n2 are the parabolic quantum numbers of that state.
The next step in this method is to consider the motion of the slow subsystem (perturbing electron) in the 'effective potential' Veff(R) consisting of the actual potential plus Enq(R). Since the constant term in equation (5) does not affect the motion, the effective potential for the motion of the perturbing electron can be represented in the form
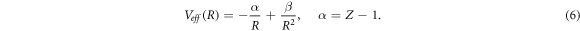
For the spectral lines of the Lyman series, since the lower (ground) state b of the radiating ion remains unperturbed (up to/including the order ∼1/R2), the coefficient β is
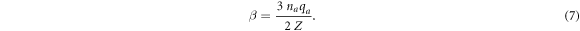
For other hydrogenic spectral lines, for taking into account both the upper and lower states of the radiating ion, the coefficient β can be expressed as
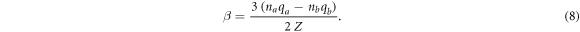
The motion in the potential from equation (6) allows an exact analytical solution. In particular, the relation between the scattering angle and the impact parameter is no longer given by equation (4), but rather becomes (see, e.g., book [7])

Here 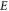 and
and  are the energy and the angular momentum of the perturbing electron, respectively. We can rewrite the angular momentum in terms of the impact parameter
are the energy and the angular momentum of the perturbing electron, respectively. We can rewrite the angular momentum in terms of the impact parameter 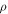 as
as
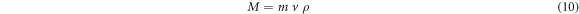
Then a slight rearrangement of equation (9) yields
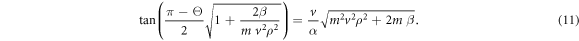
After solving equation (11) for 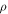 and substituting the outcome in equation (2), a more accurate expression for the electron broadening operator can be obtained. However, equation (11) does not have an exact analytic solution for
and substituting the outcome in equation (2), a more accurate expression for the electron broadening operator can be obtained. However, equation (11) does not have an exact analytic solution for 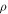 so that this could be done only numerically.
so that this could be done only numerically.
In the present paper, to get the message across in the simplest form, we will provide an approximate analytical solution of equation (11) by expanding it in powers of β. This yields (keeping up to the first power of β)
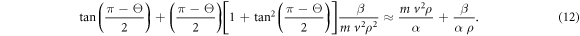
We seek the analytical solution for 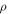 in the form
in the form 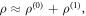 where
where 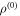 corresponds to
corresponds to  (and was given by equation (4)) and
(and was given by equation (4)) and 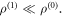 Substitution of
Substitution of 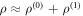 into equation (12) yields the expression
into equation (12) yields the expression
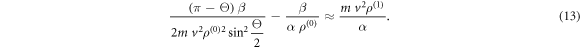
After solving equation (13) for 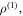 we get the expression for
we get the expression for 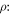
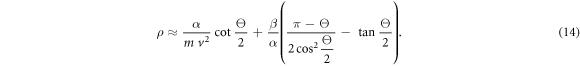
As a reminder, our goal is to perform the integration in equation (1) for obtaining a more accurate analytical result for the electron broadening operator. This can be more easily accomplished by performing the integration over 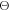 instead of
instead of  For this purpose, first we square equation (14)
For this purpose, first we square equation (14)
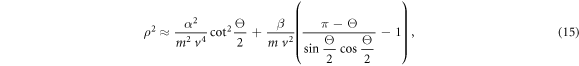
where only the first order terms in  have been kept for consistency. To make formulas simpler, we denote
have been kept for consistency. To make formulas simpler, we denote 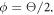 After differentiating equation (15) with respect to
After differentiating equation (15) with respect to 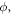 we obtain
we obtain
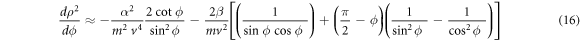
After substituting in the utmost right side of equation (2) first 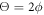 and then
and then 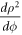 from equation (16), the contribution of the weak collisions to the electron broadening operator becomes
from equation (16), the contribution of the weak collisions to the electron broadening operator becomes
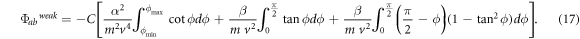
In equation (17), in the two correction terms proportional to 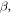 we extended the integration over the full range of the variation of the angle
we extended the integration over the full range of the variation of the angle 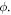 The corresponding minor inaccuracy would not contribute significantly to the electron broadening operator, since the terms involving
The corresponding minor inaccuracy would not contribute significantly to the electron broadening operator, since the terms involving 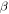 are considered to be a relatively small correction to the first term in equation (17).
are considered to be a relatively small correction to the first term in equation (17).
Performing the integrations in equation (17) we obtain:
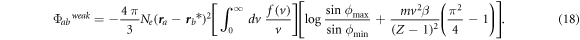
Now we add the CT estimate for the contribution of strong collisions
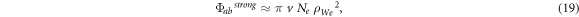
where 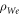 corresponds to
corresponds to  Expressions for
Expressions for 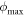 and
and  are given in paper [1] (in their equations (9) and (10a)) as follows
are given in paper [1] (in their equations (9) and (10a)) as follows
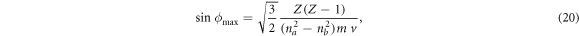

It should be emphasized that the factor  in the denominator of the right side of equation (20) was an approximate allowance by the authors of paper [1] for the contribution of the lower level b while estimating the operator (
in the denominator of the right side of equation (20) was an approximate allowance by the authors of paper [1] for the contribution of the lower level b while estimating the operator (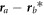 ) for hydrogenic lines of spectral series other than the Lyman lines. However, for the Lyman lines the lower (ground) level does not contribute to electron broadening operator, so that for the Lyman lines equation (20) should be simplified as follows:
) for hydrogenic lines of spectral series other than the Lyman lines. However, for the Lyman lines the lower (ground) level does not contribute to electron broadening operator, so that for the Lyman lines equation (20) should be simplified as follows:
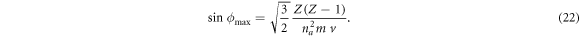
We also note that at relatively small velocities of perturbing electrons, the right side of equations (20) or (22) could exceed unity. In this case one should set  what corresponds to ρmin = 0, so that there would be no contribution from strong collisions. Typically, the range of such small velocities has a very low statistical weight in the electron velocity distribution.
what corresponds to ρmin = 0, so that there would be no contribution from strong collisions. Typically, the range of such small velocities has a very low statistical weight in the electron velocity distribution.
After substituting the above formulas for 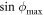 and
and 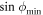 into equation (17), and combining the contributions from weak and strong collisions, we obtain the final results for the electron broadening operator:
into equation (17), and combining the contributions from weak and strong collisions, we obtain the final results for the electron broadening operator:

for the non-Lyman lines and
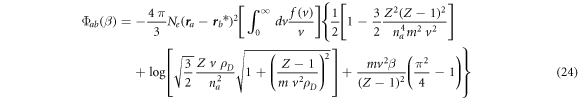
for the Lyman lines. Here and below log[...] stands for the natural logarithm.
3. Significance of the effect of non-hyperbolic trajectories
In order to determine the significance of the effect of non-hyperbolic trajectories, it is necessary to evaluate the ratio of the third term in braces in equation (24) to the first two terms in the same braces
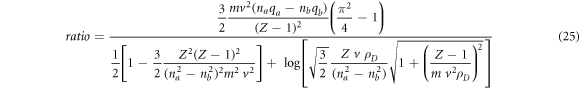
for the non-Lyman lines or the ratio
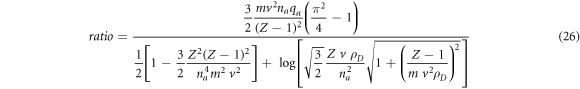
for the Lyman lines.
Below we present numerical examples for several Lyman lines. As it is customary in the Stark broadening theory, instead of the integration over velocities, for the numerical examples we use the mean thermal velocity vT of the perturbing electrons. In atomic units, the mean thermal velocity vT, the Debye radius ρD, and the reduced mass can be expressed as follows
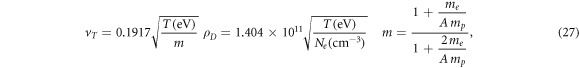
where 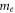 is the electron mass,
is the electron mass, 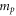 is the proton mass, and
is the proton mass, and 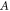 is the atomic number of the radiating ion
is the atomic number of the radiating ion 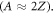
Table 1 presents the values of the ratio from equation (26) for several Lyman lines of He II at the temperature T = 8 eV and the electron density  cm−3.
cm−3.
Table 1.
Ratio from equation (26) for the Stark components of several Lyman lines of He II at the temperature T = 8 eV and the electron density  cm−3.
cm−3.
| n | ∣q∣ |

|
|---|---|---|
| 2 | 1 | 0.3261 |
| 3 | 1 | 0.3748 |
| 3 | 2 | 0.7496 |
| 4 | 1 | 0.5156 |
| 4 | 2 | 1.0311 |
| 4 | 3 | 1.5467 |
Figure 1 shows the ratio from equation (26) versus the electron density Ne for the Stark components of the electric quantum number ∣q∣ = 1 of Lyman-alpha (n = 2), Lyman-beta (n = 3), and Lyman-gamma (n = 4) lines of He II at the temperature T = 8 eV.
Figure 1. Ratio from equation (26) versus the electron density Ne for the Stark components of the electric quantum number ∣q∣ = 1 of Lyman-alpha (n = 2), Lyman-beta (n = 3), and Lyman-gamma (n = 4) lines of He II at the temperature T = 8 eV.
Download figure:
Standard image High-resolution imageIt is seen that for the electron broadening of the Lyman lines of He II, the allowance for the effect under consideration indeed becomes significant already at electron densities Ne ∼ 1017 cm−3 and increases with the growth of the electron density. It should be noted that when the ratio, formally calculated by equation (26), becomes comparable to unity, this is the indication that the approximate analytical treatment based on expanding equation (11) up to the first order of parameter β, is no longer valid. In this case the calculations should be based on solving equation (11) with respect to ρ without such approximation.
4. Conclusions
In this paper we considered the electron broadening of hydrogenlike spectral lines in plasmas more accurately than in the CT. In distinction to the CT, we treated it as a three-body problem involving the perturbing electron, the nucleus, and the bound electron. We employed the standard analytical method of separating rapid and slow subsystems by using the fact that the characteristic frequency of the motion of the bound electron around the nucleus is much higher than the characteristic frequency of the motion of the perturbing electron around the radiating ion.
With the help of this method we obtained more accurate analytical results for the electron broadening operator compared to the CT. By examples of the electron broadening of the Lyman lines of He II, we demonstrated that the allowance for this effect becomes significant at electron densities Ne ∼ 1017 cm−3 and very significant at higher densities.
It is important to emphasize that we were able to obtain the above analytical results primarily due to the underlying fundamental symmetry of the class of potentials V(R) = –A/R + B/R2, where A and B are constants. Namely, this class of potentials possesses an additional conserved quantity Meff2 = M2 + 2 mB, where M is the angular momentum and m is the mass of a particle, so that Meff is the effective angular momentum. As for the impact approximation, it was not crucial to our work—we used it only for the following two purposes: first, to get the message across in a simple form, and second, for the comparison with the CT (in which the impact approximation was crucial), so that we would compare 'apples to apples' rather than 'apples to oranges'. A brief outline of the impact approximation is presented in appendix B.
We also mention that in 1981, Baryshnikov and Lisitsa [8] published very interesting results for the electron broadening of hydrogenlike spectral lines in plasmas (also presented later in book [9]) in frames of the quantum theory of the dynamical Stark broadening, while we obtained our results in frames of the semiclassical theory of the dynamical Stark broadening, just as in the CT. (For clarity: in the semiclassical theory, the radiating atom/ion is treated quantally, while perturbing electrons classically; in the quantum theory both the radiating atom/ion and perturbing electrons are treated quantally.) Both in paper [8] and in our paper, there was used the underlying symmetry of the class of potentials V(R) = −A/R + B/R2 for obtaining analytical solutions.
A specific result for the line width Baryshnikov and Lisitsa [8] obtained for Lyman lines in the classical limit using the impact approximation, as presented in their equations (4.5) and (4.6). We compared their results from equations (4.5) and (4.6) with the CT [1] for He II Lyman lines. It turned out that for Ne ∼ (1017–1018) cm−3, i.e. for the range of electron densities, in which the overwhelming majority of measurements of the width of He II lines were performed, Baryshnikov-Lisitsa's line width exceeds the CT line width by two orders of magnitude or more. In view of the fact that the width of He II lines, measured by various authors in benchmark experiments (i.e., experiments where plasma parameters were measured independently of the line widths), never exceeded the CT width by more than a factor of two (see, e.g., benchmark experiments [10–12]), this seems to indicate that equations (4.5) and (4.6) from paper [8] are inapplicable for He II lines (indeed, the validity condition for equations (4.5) and (4.6) from paper [8], which is Z ≫ n2, is not met). In distinction, the corrections to the CT that we introduced in the present paper, do not exceed the factor of two for He II lines in the range of Ne ∼ (1017–1018) cm−3.
Appendix A.: Validity of using the analytical method based on separating rapid and slow subsystems
The characteristic frequency of the motion of the perturbing electron around the radiating ion in the process of the Stark broadening of spectral lines is the so-called Weisskopf frequency
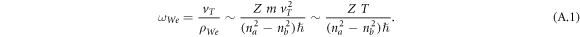
The characteristic frequency of the motion of the bound electron around the nucleus is the frequency of the spectral line
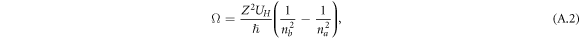
where UH is the ionization potential of hydrogen. The ratio of these two frequencies is
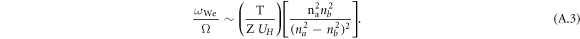
For the simplicity of estimating this ratio, let us consider na ≫ nb, so that
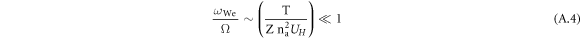
as long as
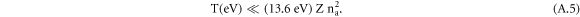
For example, for Z = 2 the above validity condition becomes
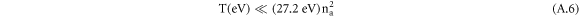
and is satisfied for a broad range of temperatures, at which He II spectral lines are observed in plasmas.
Appendix B.: Brief outline of the impact approximation in the Conventional Theory (CT) of the Stark broadening of spectral lines in plasmas
The dynamical broadening of spectral lines in plasmas by electrons is effective if the number νWe of perturbing electrons in the sphere of the electron Weisskopf radius ρWe is much smaller than unity (see, e.g., review by Lisitsa [13]): νWe = 4πNeρWe3/3 ≪ 1, where ρWe ∼ n2 ħ/(mevTe), n is the principal quantum number of the radiator energy level involved in the radiative transition, and vTe is the mean thermal velocity of plasma electrons. Under this condition, for the overwhelming majority of perturbing electrons, the characteristic frequency of the variation of the electron microfield Ωe ∼ vTe/ρWe is much greater than the instantaneous Stark splitting in the electron microfield. Physically the electron Weisskopf radius is related to the impact parameters ρ ∼ ρWe that contribute most effectively to the dynamical Stark broadening of spectral lines by electrons in plasmas [13].
The gist of dynamical effects in the Stark broadening of spectral lines in plasmas by electrons is the following. Collisions with plasma electrons cause virtual transitions mostly within the upper (n) and lower (n') multiplets during the radiative transition
n ↔ n'. The primary outcome is a decrease of the lifetime of the states n' and/or n of the radiator, thus leading to the broadening of the corresponding spectral line1 .
The fact that virtual transitions occur mostly within the upper and lower multiplets conventionally leads to so-called no-quenching approximation, in which virtual transitions between states of different principal quantum numbers are totally disregarded. This approximation allows to introduce a line space: a direct product of the Hilbert space, spanned on the basis vectors of the n-shell, with the Hilbert space, spanned on the (complex-conjugated) basis vectors of the n'-shell.
Both the impact formalism (developed by Baranger [14] and then by Kolb and Griem [15]) and the key features of the unified formalism (developed by Vidal, Cooper, and Smith [16]) can originate from the same sequence of mathematical operations—see, e.g., review by Sahal-Brechot [17]. The primary difference between them is the following. The impact formalism considers only completed collisions, while the unified formalism allows also for incomplete collisions. (Another distinction is that the unified formalism allows in principle a transition to the nearest-neighbor quasistatic result in the wings of the spectral line—this is a less important distinction because numerically the unified theory does not always yield such transition correctly.)
The most important step toward the impact formalism is the introduction of a coarse-grained time scale Δt, chosen such that
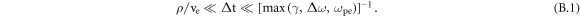
Here γ is the inversed lifetime of the radiator (the impact width of the spectral line is of the order of γ), Δω is the detuning from the unperturbed frequency ω0 of the spectral line, ωpe = (4πNee2/me)1/2 is the plasma electron frequency. Physically, the coarse-grained time scale means that one gives up details of the evolution of the radiator during the time ∼ρ/ve (which is the characteristic time of the individual collision). Instead, the focus is at the evolution of the radiator during the time intervals ∼Δt defined by equation (B.1). The possibility of introducing the coarse-grained time scale controls the limits of validity of the impact formalism. We note that in the unified formalism, the left strong inequality of equation (B.1) is relaxed to: ρ/ve ↕ Δt.
The electron broadening operator Φab is defined via the time evolution operators Ua and Ub for the upper (a) and lower (b) multiplets in the line space, respectively, as follows (see, e.g., review [13]):
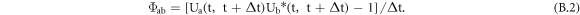
Under the impact approximation Δt ≫ ρ/ve, within the interval (t, t + Δt) the time evolution operators in equation (B.2) are replaced by the corresponding scattering matrices Sa and Sb, leading to equation (1) of the main text. We note that the terminology of having not one, but two scattering matrices Sa and Sb is related to the concept of the line space and is used in the entire extensive scope of literature on the impact broadening of spectral lines in plasmas.
Finally we note that the dynamical Stark broadening of any hydrogenic spectral lines (whether Lyman or non-Lyman) in plasmas by electrons occurs in the overlapping regime: the Stark components of any hydrogenic spectral line become overlapping. This is true even for the simplest hydrogenic line Lyman-alpha, as shown in detail, e.g., by Strekalov and Burshtein [18].
Footnotes
- 1
For clarity: the duration of the radiative transition in plasmas is ∼γ –1, where generally γ = γe + γdi + γhept + γn. Here γe, γdi, γhept, and γn are the contributions, respectively, by electrons, dynamic part of ions, high-frequency electrostatic plasma turbulence, and the natural width.


