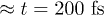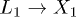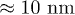Abstract
We use an atomistic approach to provide a novel and ground-breaking interpretation of the ultra-fast carriers relaxation in a realistic material: bulk silicon. By comparing the results of ab initio simulations with recent two-photon photo-emission measurements we show that the description of the carrier relaxation in terms of 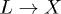 inter-valley scattering is not correct. The ultra-fast dynamics measured experimentally is, instead, due to the scattering between degenerate L states that is activated by the non-symmetric population of the conduction bands induced by the laser field. This ultra-fast relaxation is, then, entirely due to the specific experimental setup and it can be interpreted by introducing a novel definition of the quasi-particle lifetimes in an out-of-equilibrium context.
inter-valley scattering is not correct. The ultra-fast dynamics measured experimentally is, instead, due to the scattering between degenerate L states that is activated by the non-symmetric population of the conduction bands induced by the laser field. This ultra-fast relaxation is, then, entirely due to the specific experimental setup and it can be interpreted by introducing a novel definition of the quasi-particle lifetimes in an out-of-equilibrium context.
Export citation and abstract BibTeX RIS
Introduction
Silicon (Si) is a fundamental building block of semiconductors physics and microelectronics industry [1]. The miniaturization of Si-based devices to the nano-scale regime and the never-ending search for faster devices call for a deep understanding of the fundamental quantum-mechanical process that governs the ultra-short time dynamics of electrons and holes [2,3]. Most of the knowledge of the electronic and optical properties of Si remain, however, limited to the equilibrium regime. Only recently the development of ultra-fast laser pulses [4,5] has opened the opportunity to directly investigate the real-time dynamics in the non-equilibrium (NEQ) regime [6].
In real-time experiments the system is initially perturbed with a short laser pulse (the pump) followed by a second weaker pulse (the probe) that measures a specific physical observable like, for example, the absorption [7,8] or the photo-emission [9,10] spectra. The dynamics induced by the pump is, then, monitored by observing and analyzing the modifications induced in these observable by the presence of photo-excited carriers.
Despite the enormous experimental interest and the continuous development of more refined experimental techniques, the simulation methods are still based either on equilibrium first-principles approaches or on NEQ model Hamiltonians.
In the case of model Hamiltonians the relaxation paths can be calculated by using the NEQ Green's function [2,11,12] or the Monte Carlo [13] methods. The advantage of these approaches is that the modifications induced by the presence of photo-excited charges are correctly taken into account in the evaluation of the scattering transitions. However ad hoc parameters must be introduced to describe both the photo-excitation process and the specific material properties.
First-principles simulations are commonly performed by using time-dependent density-functional theory (DFT) [14] or equilibrium many-body perturbation theory [15]. In the first case the coupling with the laser pulse is described but the dissipative processes are neglected [16] or described in an empirical way [17]. In the second case the laser pulse is replaced by some ad hoc initial guess of the carriers distribution and the scattering rates are derived from the equilibrium quasi-particle (QP) lifetimes [18].
In this letter we demonstrate that an ab initio description of both the photo-excitation process and of the time dependence of the carrier scattering rates is essential for the correct interpretation of the experimental results. In particular we will reproduce the time evolution carriers in bulk Si, observed in a recent two-photons photo-emission (2PPE) experiment [9,10], without relying on any parameter. We will highlight and discuss the different scattering channels created by the pump excitation showing the existence of two different decay regimes: an ultra-fast regime due to transitions between energetically degenerated states, made possible by the symmetry breaking caused by the pump pulse; and a slower regime, where the carriers are taken to the minimum of the conduction band. In addition we will investigate the very fundamental problem of defining the lifetime of a photo-excited carrier. We will show that this definition differs from the equilibrium case, also at a very low carriers concentration. Moreover this lifetime time dependence will clearly mark the different regimes (fast and slow) of the carrier relaxation.
Method
Our theoretical framework is based on a non-linear equation for the time-dependent occupation factors [19], fi(t) ( represents a general band, n, and reciprocal space point, k):
represents a general band, n, and reciprocal space point, k):
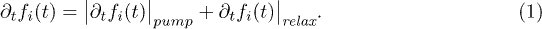
All ingredients of eq. (1) are calculated ab initio [20,21] by using DFT [22]. 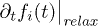 could be derived by using a standard semi-classical Boltzmann approach [2]. Instead
could be derived by using a standard semi-classical Boltzmann approach [2]. Instead  requires an approach based on Green's functions. This is, indeed, the why we use NEQ Green's function theory, reducing the complex quantum kinetic Baym-Kadanoff equations to the full set of eqs. (1)–(5) we are going to present. The detailed derivation is described in refs. [19,23]. It is indeed possible to show that the quantum kinetic equations reduce, within a completed collision approximation [19,24], to a Boltzmann-like equation, with a smeared out energy conservation, plus a coherent term which describes the creation of carriers in presence of an external field.
requires an approach based on Green's functions. This is, indeed, the why we use NEQ Green's function theory, reducing the complex quantum kinetic Baym-Kadanoff equations to the full set of eqs. (1)–(5) we are going to present. The detailed derivation is described in refs. [19,23]. It is indeed possible to show that the quantum kinetic equations reduce, within a completed collision approximation [19,24], to a Boltzmann-like equation, with a smeared out energy conservation, plus a coherent term which describes the creation of carriers in presence of an external field.
Thus, in our approach, eq. (1) originates from the diagonal terms of the equation of motion for time-diagonal NEQ Green's function, i.e. the time-dependent density matrix:  . This is a matrix in the electronic basis
. This is a matrix in the electronic basis 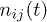 , whose diagonal elements can be interpreted [2] as NEQ occupation factors,
, whose diagonal elements can be interpreted [2] as NEQ occupation factors, 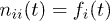 . The general equation has the form
. The general equation has the form

Here U describes, in the length gauge, the coupling with external pump field: 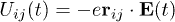 . It is chosen to reproduce the exact experimental setup. The dynamics is governed by the DFT Kohn-Sham [22] Hamiltonian, HKS, corrected by equilibrium many-body effects,
. It is chosen to reproduce the exact experimental setup. The dynamics is governed by the DFT Kohn-Sham [22] Hamiltonian, HKS, corrected by equilibrium many-body effects, 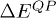 , with
, with 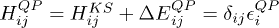 . The deviation from equilibrium of the "Hartree plus exchange correlation effects" are described by the
. The deviation from equilibrium of the "Hartree plus exchange correlation effects" are described by the ![${\Delta\Sigma}[n]$](https://content.cld.iop.org/journals/0295-5075/110/4/47004/revision1/epl17103ieqn12.gif) operator. The equation for
operator. The equation for 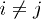 exactly reduces, within the linear regime, to the well-known Bethe-Salpeter equation [15,23] if: i) Σ is evaluated within a "Hartree plus statically screened Fock" approximation and ii) we use
exactly reduces, within the linear regime, to the well-known Bethe-Salpeter equation [15,23] if: i) Σ is evaluated within a "Hartree plus statically screened Fock" approximation and ii) we use  with
with  , a constant de-phasing of the polarization. such equation accounts for excitonic effects and, thus, ensures a very accurate description of the interaction with the laser pulse.
, a constant de-phasing of the polarization. such equation accounts for excitonic effects and, thus, ensures a very accurate description of the interaction with the laser pulse.
The term 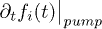 originates from the commutator on the r.h.s. of eq. (2) and describes the creation of carriers by the interaction between the polarization and the external field. Thus, the equation for
originates from the commutator on the r.h.s. of eq. (2) and describes the creation of carriers by the interaction between the polarization and the external field. Thus, the equation for 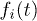 is coupled to the one for nij, i.e. the polarization
is coupled to the one for nij, i.e. the polarization  , and the two must be propagated together.
, and the two must be propagated together.
The term 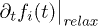 originates from the last two terms on the r.h.s. of eq. (2). It describes the relaxation and dissipation of the photo-excited carriers. It ensures that the carriers dissipate energy and scatter with phonons and electrons in such a way to relax towards the lowest energy states and has the form
originates from the last two terms on the r.h.s. of eq. (2). It describes the relaxation and dissipation of the photo-excited carriers. It ensures that the carriers dissipate energy and scatter with phonons and electrons in such a way to relax towards the lowest energy states and has the form
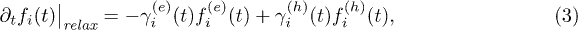
with 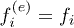 and
and 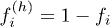 the electron and the hole occupations. In this case the dynamics is fully dictated by the electron and hole lifetimes,
the electron and the hole occupations. In this case the dynamics is fully dictated by the electron and hole lifetimes, 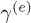 and
and  , include both an electron-phonon (e-p) and an electron-electron (e-e) contribution:
, include both an electron-phonon (e-p) and an electron-electron (e-e) contribution: 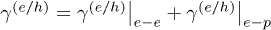 .
.
In the e-p channel we have

while in the e-e channel

Here 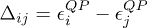 and λ represents a generic phonon mode with momentum q and branch η.
and λ represents a generic phonon mode with momentum q and branch η.  and
and 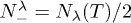 , with
, with 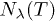 the Bose distribution function at energy
the Bose distribution function at energy 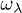 and temperature T. W is the statically screened Couloumb interaction. The P functions represent a smeared energy conservation condition. Finally,
and temperature T. W is the statically screened Couloumb interaction. The P functions represent a smeared energy conservation condition. Finally, 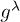 are the screened ionic potential derivatives, calculated within density-functional perturbation theory [25,26]. We have verified that, in the present work, the e-e scattering channel have only a negligible effect on the carrier dynamics due to the very low density of the photo-excited electrons. This is in agreement with the results of recent simulations [18,27,28].
are the screened ionic potential derivatives, calculated within density-functional perturbation theory [25,26]. We have verified that, in the present work, the e-e scattering channel have only a negligible effect on the carrier dynamics due to the very low density of the photo-excited electrons. This is in agreement with the results of recent simulations [18,27,28].
Equations (3)–(5) make clear the different role played by 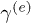 and
and 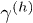 . They describe the elemental process where an initial electron (hole) is scattered in another electron (hole) emitting or absorbing an electron-hole pair (e-e channel) [3] or a phonon [3,29,30]. In the e-p case the energy is transferred back and forth from the electronic to the phonon sub-systems until a thermal equilibrium is reached [2]. Thus, eq. (3) describes both relaxation and dissipation. In the
. They describe the elemental process where an initial electron (hole) is scattered in another electron (hole) emitting or absorbing an electron-hole pair (e-e channel) [3] or a phonon [3,29,30]. In the e-p case the energy is transferred back and forth from the electronic to the phonon sub-systems until a thermal equilibrium is reached [2]. Thus, eq. (3) describes both relaxation and dissipation. In the 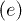 channel the term
channel the term 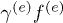 describes the removal of electrons from the state
describes the removal of electrons from the state 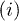 and gives a negative contribution to
and gives a negative contribution to 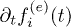 , while
, while  describes removal of holes, thus the filling of the state
describes removal of holes, thus the filling of the state  , and gives a positive contribution.
, and gives a positive contribution.
The two-photon photo-emission experiment
In the 2PPE experiment we aim at describing [9,10], a Si wafer, oriented both along the [111] and the [100] surface directions, is excited with a laser pulse at room temperature. The photo-excited sample is, then, probed with a second laser pulse that photo-emits in the continuum the excited carriers. The photo-emitted current of electrons is measured as a function of the time delay between the pump and the probe. The final result is a measure of the time-dependent occupation of the valence bands (represented by the dots in the main frame of fig. 1). More specifically we consider the population of carriers near the point L1, i.e. at 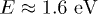 above the Fermi level1
.
above the Fermi level1
.
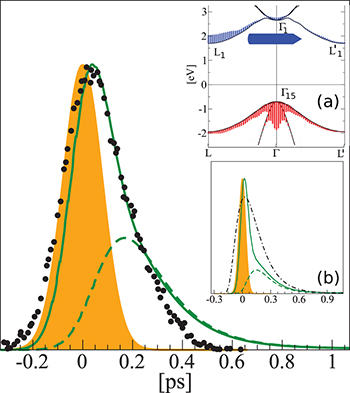
Fig. 1: (Color online) The time-dependent occupations of the L1 (green continuous line) and  (green dashed line) levels are compared with experimental data (black dots) from ref. [9]. The envelope of the laser pulse is also represented (orange shadow). In the inset (a) the carriers population (electrons in blue, holes in red) is superimposed on the band structure at t = 0. The blue arrow indicates the direction of the ultra-fast
(green dashed line) levels are compared with experimental data (black dots) from ref. [9]. The envelope of the laser pulse is also represented (orange shadow). In the inset (a) the carriers population (electrons in blue, holes in red) is superimposed on the band structure at t = 0. The blue arrow indicates the direction of the ultra-fast 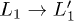 scattering process. In the inset (b) the dynamics with a shorter laser pulse
scattering process. In the inset (b) the dynamics with a shorter laser pulse 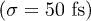 is compared with a gedanken experiment (black dot-dashed line) where the same density of carriers is placed by hand at t = 0 in the
is compared with a gedanken experiment (black dot-dashed line) where the same density of carriers is placed by hand at t = 0 in the 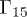 state. With the shorter pulse, the difference between the fast
state. With the shorter pulse, the difference between the fast 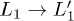 scattering and the slower
scattering and the slower 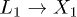 transitions becomes evident.
transitions becomes evident.
Download figure:
Standard imageWe thus consider the electronic real-time dynamics in bulk Si, under the action of a laser pulse, whose parameters are taken directly from the 2PPE experiment [9,10]. The pulse is centered at around 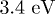 , with duration (the full width at half-maximum) of
, with duration (the full width at half-maximum) of  and intensity of
and intensity of 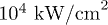 corresponding to an electric-field intensity of
corresponding to an electric-field intensity of 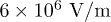 . The total fluence is
. The total fluence is 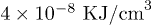 , which means that the pump field creates a carrier density of about
, which means that the pump field creates a carrier density of about 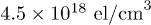 ,
, 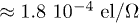 where Ω is the unit cell. As the laser transferred momentum is negligible, on the scale of the solid unit cell size, all pumped carriers are excited vertically from the valence to the conduction bands along the
where Ω is the unit cell. As the laser transferred momentum is negligible, on the scale of the solid unit cell size, all pumped carriers are excited vertically from the valence to the conduction bands along the 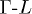 line.
line.
In fig. 1 the experimental occupation of the L1 state (dots) is compared with the solution of eq. (1) (continuous line). The agreement between theory and experiment is excellent. Both the gradual filling and emptying of the L1 state follows quite nicely the experimental curve. The theoretical results correctly describe the ultra-fast decay time-scale 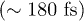 and the
and the  shift of the population peak from the maximum of the pump pulse.
shift of the population peak from the maximum of the pump pulse.
The 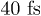 delay reflects the delicate balance between the photo-excitation and the e-p scattering and can only be described by treating both processes on the same footing.
delay reflects the delicate balance between the photo-excitation and the e-p scattering and can only be described by treating both processes on the same footing.
Experimentally [9,10] the ultra-fast decay of the L1 state is interpreted as due to 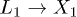 transitions. However, a deeper analysis of the theoretical result reveals a different scenario.
transitions. However, a deeper analysis of the theoretical result reveals a different scenario.
In fig. 1(a), the population of the levels at t = 0 is shown. Blue lines represent charges added and red lines charges removed. The band structure is computed along the  high symmetry path in the Brillouin zone (BZ). In bulk Si L and
high symmetry path in the Brillouin zone (BZ). In bulk Si L and 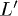 are equivalent points but fig. 1(a) shows that the level
are equivalent points but fig. 1(a) shows that the level  is not populated and most of the carriers are injected in the L1 level.
is not populated and most of the carriers are injected in the L1 level.
The symmetry breaking mechanism
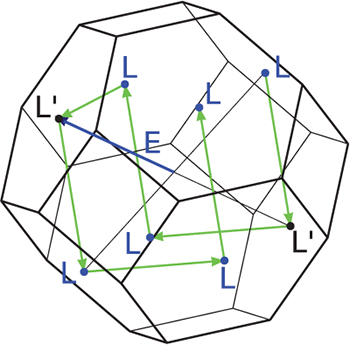
This symmetry breaking mechanism is made possible by the external field (U(t) operator in eq. (1)) which, in the 2PPE experiment, is polarized along the crystallographic [111] direction. This breaks the 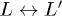 symmetry as the operation that moves L in
symmetry as the operation that moves L in 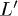 , although being a symmetry of the unperturbed system, does not leave the [111] direction unchanged (see also fig. 2). In practice this means that eq. (1) does not respect this symmetry anymore and k-points connected by a rotation that does not leave the pumping field unchanged are populated in a different way [31]. Electrons are injected in the conduction band along the
, although being a symmetry of the unperturbed system, does not leave the [111] direction unchanged (see also fig. 2). In practice this means that eq. (1) does not respect this symmetry anymore and k-points connected by a rotation that does not leave the pumping field unchanged are populated in a different way [31]. Electrons are injected in the conduction band along the  line but not, for symmetry reasons, along the
line but not, for symmetry reasons, along the  line. This is clearly shown in fig. 1 where the population of the
line. This is clearly shown in fig. 1 where the population of the 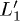 state is represented with a dashed line. The
state is represented with a dashed line. The 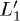 state is gradually filled while L1 is depleted revealing that the real source of the ultra-fast decay observed experimentally is the
state is gradually filled while L1 is depleted revealing that the real source of the ultra-fast decay observed experimentally is the 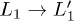 scattering.
scattering.
Fig. 2: (Color online) The primitive 3D Brillouin zone of silicon with the 8 equivalent L-points highlighted. In the presence of a linearly polarized pulse along any of the directions 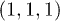 ;
; 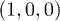 ;
; 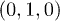 or
or 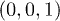 used in the 2PPE experiment [9,10] the 8 L-points are broken into two sub-groups L and
used in the 2PPE experiment [9,10] the 8 L-points are broken into two sub-groups L and  .
.
Download figure:
Standard imageThis scattering is faster than any other scattering as it involves states with the same energy. Indeed fig. 1 shows that initially the dynamics equilibrates the populations of the L1 and 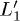 states which reach the same value at
states which reach the same value at 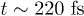 . After this point both states decay simultaneously by using the slower
. After this point both states decay simultaneously by using the slower 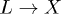 channel towards the conduction band minimum (CBM)2
. After
channel towards the conduction band minimum (CBM)2
. After 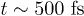 the electrons (holes) can be already described by two Fermi distributions around the CBM VBM (=valence band maximum) with very high temperatures (
the electrons (holes) can be already described by two Fermi distributions around the CBM VBM (=valence band maximum) with very high temperatures (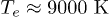 for electrons and
for electrons and 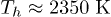 for hole). Once the Fermi distributions are created, the relaxation process is mostly dissipative and phonons are emitted in order to cool the carriers temperatures (after
for hole). Once the Fermi distributions are created, the relaxation process is mostly dissipative and phonons are emitted in order to cool the carriers temperatures (after 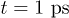 , for example we obtain,
, for example we obtain, 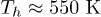 and
and 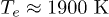 ).
).
A gedanken experiment
To better disentangle the 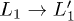 process from the slower
process from the slower 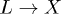 channel we consider a shorter laser pulse with
channel we consider a shorter laser pulse with 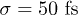 . We also consider a gedanken experiment where electrons are manually excited. One of the approximations most widely used in the literature is to mimic the effect of the laser pulse with some, ad hoc, initial population of carriers in the valence bands. This approximation corresponds to put U = 0 in eq. (2) defining some initial arbitrary population
. We also consider a gedanken experiment where electrons are manually excited. One of the approximations most widely used in the literature is to mimic the effect of the laser pulse with some, ad hoc, initial population of carriers in the valence bands. This approximation corresponds to put U = 0 in eq. (2) defining some initial arbitrary population 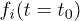 . Here we have chosen an initial population around the
. Here we have chosen an initial population around the 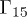 state, with a carrier density equal to the one measured experimentally.
state, with a carrier density equal to the one measured experimentally.
We then show (fig. 1(b)) the population of the L1 state in the gedanken experiment (dot-dashed line), and when the photo-excitation is performed with the shorter pulse for both L1 (continuous line) and 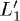 (dashed line). By comparing the results we notice that the decay of the L1 state, when the carriers are manually excited is much slower compared to the case when the carriers are photo-excited. This is because the dynamics following the ad hoc population is symmetric and the L1 and
(dashed line). By comparing the results we notice that the decay of the L1 state, when the carriers are manually excited is much slower compared to the case when the carriers are photo-excited. This is because the dynamics following the ad hoc population is symmetric and the L1 and 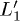 are equally populated. The ultra-fast
are equally populated. The ultra-fast 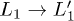 channel is switched off. Instead, when the shorter pump pulse is considered, the two decay time-scales (the ultra-fast
channel is switched off. Instead, when the shorter pump pulse is considered, the two decay time-scales (the ultra-fast 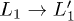 and the slower
and the slower 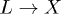 ) are clearly visible. Immediately after the population peak we notice an almost vertical drop of the L1 population. The characteristic time scale is even faster
) are clearly visible. Immediately after the population peak we notice an almost vertical drop of the L1 population. The characteristic time scale is even faster 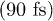 than the one measured experimentally
than the one measured experimentally 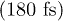 , and still dictated by the length of the laser pulse. After the vertical drop we notice a smoother decay of both the L1 and the
, and still dictated by the length of the laser pulse. After the vertical drop we notice a smoother decay of both the L1 and the 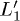 occupations, induced by the much slower
occupations, induced by the much slower  channel.
channel.
Carrier lifetimes: an out-of-equilibrium concept
The most time-consuming part of solving eq. (1) is the update of the 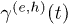 functions whose dependence on the occupations must be re-calculated at each time step. A very tempting possibility would be to keep
functions whose dependence on the occupations must be re-calculated at each time step. A very tempting possibility would be to keep 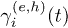 constant. This is indeed the main ingredient of the relaxation time approximation (RTA) that is based on the assumption that
constant. This is indeed the main ingredient of the relaxation time approximation (RTA) that is based on the assumption that  , with
, with 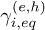 the equilibrium lifetimes, calculated without the presence of any external field3
. This approach has been recently used in ref. [18] to describe the carrier relaxation in Si excited by the weak sunlight.
the equilibrium lifetimes, calculated without the presence of any external field3
. This approach has been recently used in ref. [18] to describe the carrier relaxation in Si excited by the weak sunlight.
In order to investigate further the meaning of the 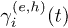 time dependence and their crucial role in describing the experimental results, let us introduce the totally relaxed occupations,
time dependence and their crucial role in describing the experimental results, let us introduce the totally relaxed occupations, 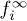 , defined as the occupations at the time trel such that
, defined as the occupations at the time trel such that 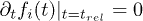 . From eq. (1) and eq. (3) it follows that
. From eq. (1) and eq. (3) it follows that
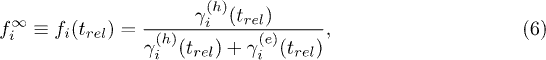
where we have used the fact that at 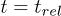 the pump field is switched off and
the pump field is switched off and  .
.
In the equilibrium regime the dependence of the 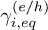 lifetimes on the electronic energies is well known. Indeed for conduction bands
lifetimes on the electronic energies is well known. Indeed for conduction bands 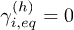 while for valence states
while for valence states 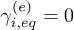 . This means that, from eq. (6), the totally relaxed occupations would be zero for any conduction band.
. This means that, from eq. (6), the totally relaxed occupations would be zero for any conduction band.
This is the reason why in the RTA [18] 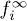 is added as an adjustable parameter in the simulation. It is commonly parametrized as a Fermi distribution with a given temperature and chemical potential. But our simulations reveal that, in general, electrons and holes are distributed with two different Fermi distributions. This means two different chemical potentials and temperatures. In our approach
is added as an adjustable parameter in the simulation. It is commonly parametrized as a Fermi distribution with a given temperature and chemical potential. But our simulations reveal that, in general, electrons and holes are distributed with two different Fermi distributions. This means two different chemical potentials and temperatures. In our approach 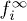 is a by-product of the simulation and it must not be provided at the beginning.
is a by-product of the simulation and it must not be provided at the beginning.
Moreover, the present scheme allows to go well beyond the RTA by formally defining a NEQ carrier lifetime, 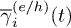 , such that occupation functions satisfy the simple equation
, such that occupation functions satisfy the simple equation  with
with
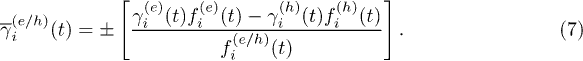
In eq. (7) the + (−) corresponds to electrons (holes). Equation (7) demonstrates that a true instantaneous NEQ carrier lifetime includes contributions from both the electron (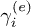 ) and the hole (
) and the hole ( ) lifetimes.
) lifetimes.
The deviation of  from
from 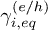 is, indeed, strictly connected with the symmetry breaking mechanism that explains the experimental result. In the
is, indeed, strictly connected with the symmetry breaking mechanism that explains the experimental result. In the 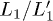 case, indeed,
case, indeed, 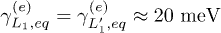 . From fig. 3 we see that, instead, both
. From fig. 3 we see that, instead, both 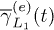 and
and 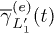 changes, during the simulation, by an order of magnitude. The reason is that, in eq. (7), the
changes, during the simulation, by an order of magnitude. The reason is that, in eq. (7), the 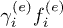 and
and  factors are of the same order and their balance measures the difference of population between the L1 and
factors are of the same order and their balance measures the difference of population between the L1 and 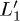 states. We can, therefore, easily recognize in fig. 3 two well-defined regimes: when
states. We can, therefore, easily recognize in fig. 3 two well-defined regimes: when 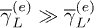 the ultra-fast
the ultra-fast 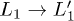 scattering channel is active. When
scattering channel is active. When 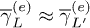 , instead, the relative L1 and
, instead, the relative L1 and 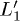 populations are balanced and the dynamics is dictated by the slower
populations are balanced and the dynamics is dictated by the slower 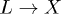 channel.
channel.
Fig. 3: (Color online) The equilibrium lifetime, 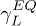 (blue dot-dashed line), is compared with the time-dependent out-of-equilibrium lifetimes defined in eq. (7) for the L1 and
(blue dot-dashed line), is compared with the time-dependent out-of-equilibrium lifetimes defined in eq. (7) for the L1 and 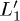 states. Due to the symmetry breaking induced by the laser pulse (the orange shadow represents its Gaussian envelope) we have two in-equivalent lifetimes at L1 (green line) and
states. Due to the symmetry breaking induced by the laser pulse (the orange shadow represents its Gaussian envelope) we have two in-equivalent lifetimes at L1 (green line) and 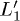 (green dashed line). Their relative intensity defines the ultra-fast
(green dashed line). Their relative intensity defines the ultra-fast  and the slow
and the slow 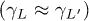 time regimes.
time regimes.
Download figure:
Standard imageA global view of the real-time dynamics
To further illustrate the results of our simulations we also show, in fig. 4, an overview of the carriers dynamics by four snapshots. The carriers distribution is represented here on the band structure4
of Si. Added (removed) carriers are in blue (red). At 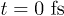 (panel (a)), corresponding to the laser pulse maximum, at
(panel (a)), corresponding to the laser pulse maximum, at 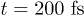 (panel (b)), when the L1 and the
(panel (b)), when the L1 and the 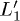 populations are almost the same, at
populations are almost the same, at 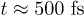 (panel (c)) when both the L1 and
(panel (c)) when both the L1 and  states are almost empty and finally after more than
states are almost empty and finally after more than 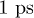 (panel (d)) when the electrons have reached the CBM. The dominant process at each time considered is schematically represented by the arrows.
(panel (d)) when the electrons have reached the CBM. The dominant process at each time considered is schematically represented by the arrows.
Fig. 4: (Color online) Time snapshots of the carriers occupations of the entire band structure taken at times 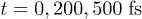 and
and 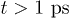 . In each snapshot the arrows schematically represent the dominant channel that drives the dynamics. The initial excitation is followed by an ultra-fast
. In each snapshot the arrows schematically represent the dominant channel that drives the dynamics. The initial excitation is followed by an ultra-fast 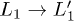 transition. Then the slower
transition. Then the slower  channel will fill the surroundings of CBM that, locally, will be populated with a high-temperature Fermi distribution. Finally, on a longer time-scale, this distribution will be cooled down and the energy transferred to the lattice.
channel will fill the surroundings of CBM that, locally, will be populated with a high-temperature Fermi distribution. Finally, on a longer time-scale, this distribution will be cooled down and the energy transferred to the lattice.
Download figure:
Standard imageConclusions
In conclusion we have presented a fully ab initio simulation of the carrier dynamics in Si. The present scheme, based on the merging of DFT with NEQ Green's function theory, successfully describes the ultra-fast decay of the L1 carrier population measured in a recent 2PPE experiment. We have also highlighted that the microscopic mechanism that drives this ultra-fast decay is not a standard inter-valley scattering but it is due to an ultra-fast (as fast as 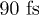 )
) 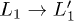 scattering channel activated by the specific polarization the pump laser. This physical interpretation is, also, supported by introducing a novel definition of the non-equilibrium carrier lifetime that provides an intuitive picture of the physical processes activated by the initial photo-excitation.
scattering channel activated by the specific polarization the pump laser. This physical interpretation is, also, supported by introducing a novel definition of the non-equilibrium carrier lifetime that provides an intuitive picture of the physical processes activated by the initial photo-excitation.
Acknowledgments
Financial support was provided by the Futuro in Ricerca grant No. RBFR12SW0J of the Italian Ministry of Education, University and Research. DS thanks G. Onida for the access granted to the etsfmi cluster in Milano and C. Attaccalite for useful discussions.
Footnotes
- 1
- 2
The decay time of our simulated L1 population matches exactly the experiment up to
 . Only at later times we see a small deviation from the measured behavior which, however, corresponds to the activation of the slower
. Only at later times we see a small deviation from the measured behavior which, however, corresponds to the activation of the slower  processes. Experimentally the laser is shone on a surface which can penetrate the sample, at the experimental wavelength, for
processes. Experimentally the laser is shone on a surface which can penetrate the sample, at the experimental wavelength, for  . Thus, the electrons have access to a large number of empty states degenerate with L1. Also surface states close in energy may exist. This explains the small deviation of our simulation from the experimental result.
. Thus, the electrons have access to a large number of empty states degenerate with L1. Also surface states close in energy may exist. This explains the small deviation of our simulation from the experimental result. - 3
- 4
The occupations and the energies on the band structure are fitted from the occupation and the energies evaluated on the double mesh used for the simulation.