Abstract
We examine interaction states between baryons in U(3) configurations. Such interaction states may represent the meson mass spectrum above the pion triplet. Our configuration space is the Lie group U(3) with a Hamiltonian structure for baryons as stationary states. Mesonic states come about via an interaction potential. The Hamiltonian can be diagonalized by a Rayleigh-Ritz method resulting in matrix element integrals that can be solved analytically for the toroidal degrees of freedom by expanding on a suitable set of base functions. We compare calculated eigenvalues for indefinite parity states to observed unflavoured meson masses.
Export citation and abstract BibTeX RIS

Published by the EPLA under the terms of the Creative Commons Attribution 4.0 International License (CC-BY). Further distribution of this work must maintain attribution to the author(s) and the published article's title, journal citation, and DOI.
Introduction
Most work on meson mass spectra select specific groups of states trying to understand them from a quark model perspective [1–2]. More fundamental are lattice gauge theory considerations based on quantum chromodynamics [3] where masses are derived from time decay of correlation functions [4]. Here a select choice of meson and baryon masses, e.g., from 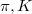 and
and 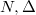 are used to settle quark masses for hadron spectroscopy. The present work wants to avoid quark masses as fitting parameters. The goal is to calculate meson masses without specific reference to quark models. Instead, we want to treat light mesons as interaction states between two baryons. We first introduce the baryons for whom the mesons act as interaction quanta under the strong interactions.
are used to settle quark masses for hadron spectroscopy. The present work wants to avoid quark masses as fitting parameters. The goal is to calculate meson masses without specific reference to quark models. Instead, we want to treat light mesons as interaction states between two baryons. We first introduce the baryons for whom the mesons act as interaction quanta under the strong interactions.
Baryons
We consider baryons as stationary states on an intrinsic U(3) Lie group configuration space. One may consider the configuration space as a generalization of an intrinsic spin space, now with nine degrees of freedom. The intrinsic dynamics to produce the baryon spectrum is a Hamiltonian structure [5],

with configuration variable 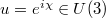 , Laplacian Δ and a Manton-like trace potential [6] radically reinterpreted from lattice gauge theory for non-pertubative quantum chromodynamics [7]. The trace potential in (1) folds out in periodic potentials of nine dynamical variables [8], see fig. 1.
, Laplacian Δ and a Manton-like trace potential [6] radically reinterpreted from lattice gauge theory for non-pertubative quantum chromodynamics [7]. The trace potential in (1) folds out in periodic potentials of nine dynamical variables [8], see fig. 1.
Fig. 1: Trace potential (10) in dynamical variables and projection of these to laboratory space. Figure taken from [16].
Download figure:
Standard imageThe scale  is set by a projection [5] of the intrinsic baryon dynamics to space. The length scale a for the projection is related to the classical electron radius
is set by a projection [5] of the intrinsic baryon dynamics to space. The length scale a for the projection is related to the classical electron radius 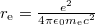 [9,10] by the expression
[9,10] by the expression 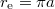 [5]. The factor π manifests the toroidal shape of the intrinsic configuration space, U(3). Our baryonic energy scale
[5]. The factor π manifests the toroidal shape of the intrinsic configuration space, U(3). Our baryonic energy scale 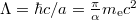 is close to the scale of quantum chromodynamics
is close to the scale of quantum chromodynamics 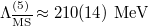 [3].
[3].
The projection scaled by a led to a compact relation for the neutron to electron mass ratio [5]

in agreement with the experimental value [3]. Here  from a Rayleigh-Ritz solution [11] of (1) with 3078 base functions —at the limit of our computer programme— and the fine structure coupling
from a Rayleigh-Ritz solution [11] of (1) with 3078 base functions —at the limit of our computer programme— and the fine structure coupling 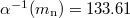 is sliding from
is sliding from 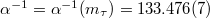 [3,12]. The Hamiltonian structure in (1) also gives good agreement with observed four star resonances for unflavoured baryons [13,14] and with the proton spin structure function [15,16].
[3,12]. The Hamiltonian structure in (1) also gives good agreement with observed four star resonances for unflavoured baryons [13,14] and with the proton spin structure function [15,16].
Unfolding the theory for baryons
To solve (1), we first express the configuration variable in nine dynamical variables 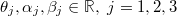 spanning the nine degrees of freedom laid out by the nine generators Tj
, Sj
,Mj
of the algebra u(3), thus
spanning the nine degrees of freedom laid out by the nine generators Tj
, Sj
,Mj
of the algebra u(3), thus

The three Tj
's generate the maximal, Abelian torus of U(3), the Sj
's are off-diagonal generators equivalent to three of the off-diagonal Gell-Mann matrices [17] and take care of spin degrees of freedom. The three Mj
's take care of flavour degrees of freedom. The nine generators are equivalent to kinematic generators in laboratory space, thus one may imagine the intrinsic degrees of freedom to be excited kinematically from laboratory space. In a coordinate representation [17] with 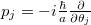 , we have, e.g.,
, we have, e.g.,

We use the Laplacian in a polar decomposition [18]

where 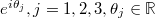 are the three eigenvalues of u in a matrix representation. The derivatives are equivalent to the toroidal generators with generalizations to left invariant coordinate fields
are the three eigenvalues of u in a matrix representation. The derivatives are equivalent to the toroidal generators with generalizations to left invariant coordinate fields 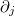 and forms
and forms 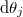 [5]
[5]

and the van de Monde determinant is [19]

The van de Monde determinant only depends on the three eigenangles
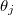 . The trace in the potential is invariant under conjugation
. The trace in the potential is invariant under conjugation 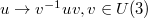 . In particular we can use a conjugation to diagonalize u to get
. In particular we can use a conjugation to diagonalize u to get

Thus, the potential likewise only depends on the eigenangles and is periodic in these [8], see fig. 1,

where

The polar decomposition (5) suits the potential (10) such that we can factorize the wave function

We namely multiply through by J with (5) and (9) inserted in (1) and introduce 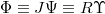 to get
to get
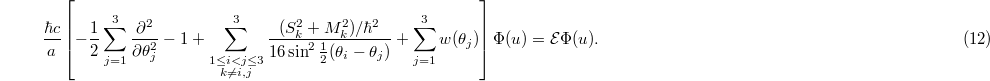
The nominator in the third term in (12) acts only on the off-toroidal degrees of freedom and we want to integrate these out like when solving the hydrogen atom [17]. This is possible by exploiting the fact that the indexing 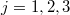 of the three sets of dynamical variables
of the three sets of dynamical variables 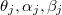 is arbitrary. Therefore, we can average over the off-toroidal degrees of freedom if only we know the spectrum of
is arbitrary. Therefore, we can average over the off-toroidal degrees of freedom if only we know the spectrum of 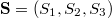 and
and 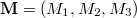 . The spectrum of the spin operators Sj
is well known,
. The spectrum of the spin operators Sj
is well known,

from the commutation relations (cf., e.g., p. 145 in [20])

Note the minus sign on the right-hand side as in intrinsic body fixed coordinate systems in nuclear physics [21]. The three operators Mj connect the algebra by commuting into the spin subalgebra generated by the three spin generators Sj

The spectrum for 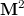 follows from a lengthy calculation [13,16]. Here we give the result
follows from a lengthy calculation [13,16]. Here we give the result

where 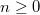 is a non-negative integer, y is the hypercharge and i3 is the isospin three-component. For
is a non-negative integer, y is the hypercharge and i3 is the isospin three-component. For 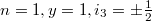 and spin
and spin 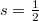 we get the minimum value
we get the minimum value

Thus, integrating out the off-toroidal degrees of freedom our problem in (12) greatly simplifies to yield for the toroidal wave function 

where the dimensionless eigenvalue 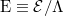 with energy scale
with energy scale  , total potential
, total potential

where the potential C and the Laplacian  are
are

As mentioned, the labelling of the eigenangles 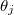 is arbitrary so the toroidal wave function
is arbitrary so the toroidal wave function 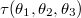 should be symmetric in these. The Jacobian J in (7), on the other hand is antisymmetric, so the measure-scaled toroidal wave function
should be symmetric in these. The Jacobian J in (7), on the other hand is antisymmetric, so the measure-scaled toroidal wave function 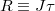 must be antisymmetric. Thus, R can be expanded on Slater determinants
must be antisymmetric. Thus, R can be expanded on Slater determinants

Colour quark fields are generated by the momentum form as 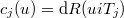 and used, e.g., for parton distribution functions, e.g., for u and d quarks with
and used, e.g., for parton distribution functions, e.g., for u and d quarks with 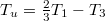 and
and 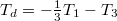 [5].
[5].
Rayleigh-Ritz method
We want to find eigenvalues 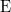 in (18) equivalent to
in (18) equivalent to

In the Rayleigh-Ritz method [11], [16] one expands the eigenfunctions on an orthogonal set of base functions with a set of expansion coefficients, multiply the equation by the complex conjugate expansion, integrates over the entire variable volume and ends up with a matrix problem in the expansion coefficients from which a set of eigenvalues can be obtained. In standard quantum mechanics lingo this is called diagonalization of the Hamiltonian. Thus with the approximation

we have the integral equation

The counting variable l in (23) is a suitable ordering of the set of triples p, q, r in (21) such that we expand on an orthogonal set. Equation (24) can be interpreted as a vector eigenvalue problem, where a is a vector, whose elements are the expansion coefficients al . Thus, (24) is equivalent to the eigenvalue problem

where the matrix elements of H and F are given by

and

When the set of expansion functions is orthogonal, (25) implies

from which we get a spectrum of N eigenvalues determined as the set of components of a vector E generated from the eigenvalues of the matrix 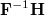 , i.e.,
, i.e.,

The lowest-lying eigenvalues will be better and better determined for increasing values of N in (23). For the base (21) the integrals (26) and (27) can be solved analytically.
The exact expressions to be used in constructing H and F are given below for the base (21). For p<q<r and s<t<u we have the following orthogonality relations:

Here we have used the Kronecker delta

The Laplacian yields

The matrix elements for the intrinsic potential (9) and the centrifugal potential C in (19) are more involved [16]. We give explicit expressions for these when considering interaction states.
Interaction states
The trace potential in (1) is half the square of the shortest geodesic d(e, u) from the origo e, the neutral element, to the configuration point 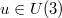 . Thus we could equally well write (1) as
. Thus we could equally well write (1) as

This form opens for the introduction of interaction states between two baryons with intrinsic configuration variables 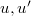 , respectively. We namely take the interaction quanta to be eigenstates of
, respectively. We namely take the interaction quanta to be eigenstates of

for proper choices of spins, hypercharges and isospins, hidden in the Laplacians for the respective configuration variables. Note that we have deliberately omitted the intrinsic potentials 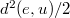 and
and 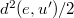 , respectively, as these relate to the intrinsic structure of the individual baryons whereas here we want to consider their interaction keeping the kinetic terms at the point of interaction. It is our task in the present work to solve (34).
, respectively, as these relate to the intrinsic structure of the individual baryons whereas here we want to consider their interaction keeping the kinetic terms at the point of interaction. It is our task in the present work to solve (34).
The shortest geodesic is left (and right) invariant, thus

by left translation with 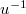 . This left invariance is what secures local gauge invariance of strong interactions in laboratory space [14,22].
. This left invariance is what secures local gauge invariance of strong interactions in laboratory space [14,22].
We shall interpret the interaction potential as a representation of unflavoured antiquark-quark states, e.g., 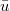 -quark
-quark 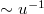 -configuration and d-quark
-configuration and d-quark 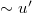 -configuration leading to mesonic interaction states. In table 1, we are therefore going to take the following set of quark quantum numbers,
-configuration leading to mesonic interaction states. In table 1, we are therefore going to take the following set of quark quantum numbers,

to get the centrifugal potentials in (12) for the configuration variables u and 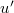 , respectively.
, respectively.
Table 1:. Light unflavoured mesons above the pion triplet compared to interaction states from (34). Isospin and spin assignments are for the observed states only. The masses for interaction states are tentative. They are sensitive to averaging over off-toroidal degrees of freedom (60). The values shown are for base sets combined from 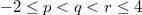 and
and 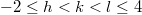 (i.e., 1225 base functions) and for
(i.e., 1225 base functions) and for 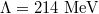 . They are given for indefinite parity Slater determinants (21).
. They are given for indefinite parity Slater determinants (21).
| Meson [3] | Quantum | Observed | Interaction |
|---|---|---|---|
| experiment | numbers | (MeV) | state |
| I, J | (MeV) | ||
| η | 0,0 | 547.862 | 452 |
| f0 | 0,0 | 400–550 | 705 |
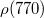
| 1,1 | 775.26 | 714 |
| ω | 0,1 | 782.65 | 809 |
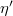
| 0,0 | 957.78 | 816 |
| f0(980) | 0,0 | 990 | 886 |
| a0 | 1,0 | 980 | 911 |
| – | – | – | – |
The new thing about making (35) operational in the interaction potential 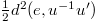 is that we cannot in general diagonalize both u and
is that we cannot in general diagonalize both u and 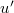 by conjugation with the same
by conjugation with the same 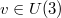 and thus the shortest geodesic cannot be expressed only by the eigenangles
and thus the shortest geodesic cannot be expressed only by the eigenangles 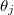 and
and 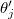 . Therefore our wave function cannot be factorized in toroidal and off-toroidal factors like in (11) for our single baryon case.
. Therefore our wave function cannot be factorized in toroidal and off-toroidal factors like in (11) for our single baryon case.
We have to find a way of averaging over the off-toroidal degrees of freedom in u and 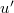 . We will do this by what we could call a one shot Monte Carlo integration. As an exemplar situation we take
. We will do this by what we could call a one shot Monte Carlo integration. As an exemplar situation we take 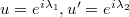 and we want to calculate the value of the interaction potential for these two configuration variables which share eigenvalues but are at finite distance. The result is (57)
and we want to calculate the value of the interaction potential for these two configuration variables which share eigenvalues but are at finite distance. The result is (57)

Calculation of off-diagonal distance
To calculate the squared distance in (37) requires quite a bit of algebra, which we here go through. To simplify we use the two-dimensional analogues of 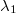 and
and 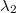

and define

With 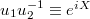 , we consider
, we consider

Now

and we have the nice relation [23]

where

and

Thus,

Omitting the unit matrix I we get

This yields

We want to exploit the conjugation relation [24]

Using (48) we can calculate the trace needed in (40) from just finding the eigenvalues of 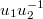 in (47). To do this we set up the eigenvalue equation
in (47). To do this we set up the eigenvalue equation

and find two complex conjugate eigenvalues,

from which the eigenvalues λ for 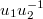 are
are

To get the eigenvalues for the generator X, we need the complex logarithm [25]

For our case we have

with the angular argument determined from (51) by

This yields by diagonalization with some 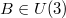

from which we get

and finally as disclosed in (37)

Integrating the trace potential in the off-diagonal degrees of freedom
We cannot factorize the wave function 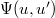 in (34) like we did in (11) because the interaction trace potential cannot be reduced to an expression containing only the eigenangles
in (34) like we did in (11) because the interaction trace potential cannot be reduced to an expression containing only the eigenangles 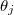 and
and 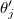 for u and
for u and 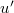 , respectively. But we can expand the measure-scaled function
, respectively. But we can expand the measure-scaled function

on factorized functions of the form

We then have

Here we used the exemplar off-toroidal average from (57) and independent diagonalizations of u and 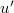 like in (8).
like in (8).
Rayleigh-Ritz matrix elements for interaction states
We here explain how to obtain matrix elements for the centrifugal terms and the interaction term from (34). In (59) we expand R and 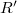 on Slater determinants (21)
on Slater determinants (21)

For clarity, below, we use the following notation:

The norm integrals follow from (30):

Note that l and o are letters, not the numbers one and zero! The subscripts 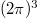 indicate that we integrate from
indicate that we integrate from  to π in all three eigenangles
to π in all three eigenangles 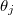 and
and 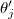 , respectively. Also the Laplacian integrals for (20) factorize
, respectively. Also the Laplacian integrals for (20) factorize

The centrifugal potential likewise comes in factors depending on the three  s and the three
s and the three 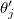 s respectively
s respectively
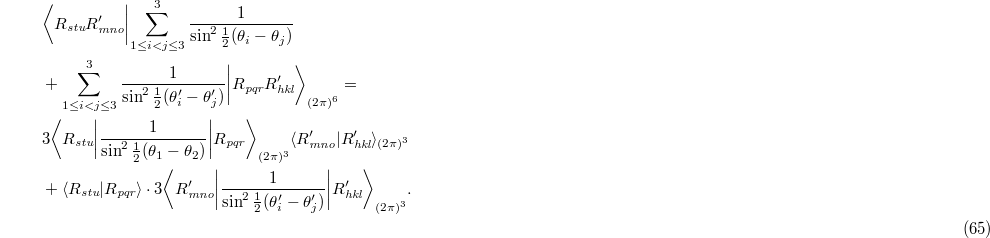
Here we exploited the arbitrary labelling of the eigenangles to make do with 3 times the terms for 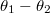 and
and  , respectively. However, to do the integrals over these factors we change variables to
, respectively. However, to do the integrals over these factors we change variables to 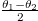 and
and  in order to manage the seemingly singular expression for
in order to manage the seemingly singular expression for 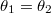 . It namely turns out that the Slater determinants can be separated in terms that suit these new variables in such a way that the integrals can be calculated analytically to give finite results.
. It namely turns out that the Slater determinants can be separated in terms that suit these new variables in such a way that the integrals can be calculated analytically to give finite results.
To do the integrals in (65) let

Then we find

Applying this we have

where the factor 4 comes from the shift of variables and nn is a shorthand notation for

from the sine integrals (cf., e.g., pp. 172–180 in [16])

Now

and with shorthand notation

our matrix element will contain nine terms

For the interaction integrals we apply a similar technique, now pairing  and
and 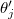 for variable shifts to
for variable shifts to 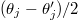 and
and 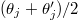 and use the shorthand notation
and use the shorthand notation

for the integral

We then have the full interaction term
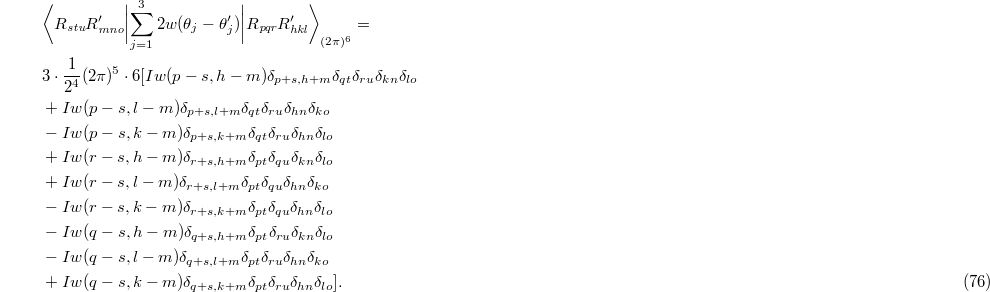
In both (73) and (76) it is understood that the index triples fulfil

This greatly reduces the number of terms in both expressions but leaves open a completenes issue. Results are shown in table 1. All results follow from a single energy scale, 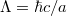 with the length scale a given by
with the length scale a given by 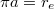 as for the baryon spectrum (1). No quark mass parameters are involved and no fitting has been undertaken. The π-mesons are treated seperately elsewhere as revived Goldstone bosons from a slightly misaligned Higgs mechanism in [26].
as for the baryon spectrum (1). No quark mass parameters are involved and no fitting has been undertaken. The π-mesons are treated seperately elsewhere as revived Goldstone bosons from a slightly misaligned Higgs mechanism in [26].
Conclusion
We have examined a model for mesons as interaction states between baryons in U(3) configurations. The model eigenstates have masses comparable to the observed unflavoured mesons above the pions. However, direct identification remains preliminary. In particular both η and 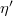 lie low —perhaps because of missing strange flavour contributions and underestimation of the off-toroidal contribution. On the other hand, f0 and f0(980) are high and low, respectively, which may be seen as missing parity splitting. Spin and isospin coupling should be specified by expansion on D-functions for off-toroidal degrees of freedom and a way to average over these for the interaction potential be sought.
lie low —perhaps because of missing strange flavour contributions and underestimation of the off-toroidal contribution. On the other hand, f0 and f0(980) are high and low, respectively, which may be seen as missing parity splitting. Spin and isospin coupling should be specified by expansion on D-functions for off-toroidal degrees of freedom and a way to average over these for the interaction potential be sought.
Acknowledgments
I thank the Technical University of Denmark for an inspiring working environment.





