Abstract
The dynamics of a magnetically forced conducting fluid in confined geometries is studied. A pseudospectral method with volume penalisation is used to solve the resistive magnetohydrodynamic equations. A helical magnetic field is imposed via boundary conditions, which generates a response in the velocity field for large enough magnitudes. Different helical structures are observed in the flow depending on the magnitude and direction of the forcing and the cross-sectional geometry of the fluid domain. A computational technique for finding a solenoidal vector field which can be used in complex geometries is also proposed.
Export citation and abstract BibTeX RIS
Communicated by Y Hattori
1. Introduction
Vortical structure formation plays an important role in magnetohydrodynamic (MHD) flows in a variety of settings and applications, such as the Earthʼs core (Moffatt 1978), metal casting, and fusion devices of the reversed field pinch (RFP) type (Taylor 1974) and of the tokamak type (Wesson 2011). The development of large rotational structures has been addressed before in Bos et al (2008) and Neffaa et al (2008). While some analytic results exist for MHD flows, we must generally rely on numerical simulations in order to understand the behaviour of those fluids in confined geometries. Understanding structures in MHD flows lends insight into the underlying mathematical properties and can help to control MHD flows more efficiently.
In this paper we explore the behaviour of a conducting fluid and the evolution of the flow topology under the influence of external magnetic forcing in two cylindrical geometries. In previous investigations we focused on the structure formation of magnetofluids in two-dimensional (Bos et al 2008, Neffaa et al 2008) and toroidally confined (Morales et al 2012) domains. The case of a cylindrical domain was considered numerically in Shan et al (1991) and Shan and Montgomery (1993b) in the case of non-penetration boundary conditions. This choice was necessary for these simulations because the fields were decomposed into eigenfunctions of the curl operator in order to observe the dynamics of helical structures, and it was argued, via an energy-minimization argument, that the dominant mode of the flow is such a helical basis function. The instability threshold, determined analytically, was confirmed numerically and the evolution of the flow with the magnitude of the forcing was described. Due to the absence of an efficient physical-space to Chandrasekhar–Kendall function-space transform, the nonlinear term was computed directly, with rapidly increasing computational cost. In this paper, we use a pseudospectral method (Canuto et al 1987) combined with a volume penalisation method for imposing boundary conditions in complex geometries (Arquis and Caltagirone 1984, Angot et al 1999). Thus we were able to implement different boundary conditions than used in Shan et al (1991) and to perform simulations in cylindrical geometries with different cross-sections. A related study, which was limited to circular cross-sections and for different parameters focusing on the RFP application can be found in Bonfiglio et al (2013) and Veranda et al (2013). The self-organization of compressible MHD flows into helical structures has also been observed in Horiuchi and Sato (1986) and Zhu (1995), for example, where the mechanism of self-organization is magnetic re-connection.
This paper is organized as follows: in section 2 we give a mathematical description of the problem and present our numerical technique. In section 3, we explore the structure of the velocity field in a circular geometry when forced by an external helical magnetic field, and we show the effect of wrapping number in section 4. Alignment statistics are discussed in section 5. Section 6 shows how the flow topology changes when the cross-section is modified. We give our conclusions and future perspectives in section 7.
2. Mathematical description and numerical method
2.1. Mathematical description
Let  denote the velocity and
denote the velocity and  the magnetic field of the conducting fluid. The time evolution of these quantities using conventional Alfvén normalized variables, is given by
the magnetic field of the conducting fluid. The time evolution of these quantities using conventional Alfvén normalized variables, is given by
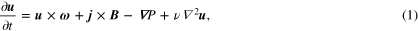

where P is the total pressure,  is the vorticity, and
is the vorticity, and  is the current density. Physical parameters are the kinematic viscosity
is the current density. Physical parameters are the kinematic viscosity  , and the magnetic diffusivity
, and the magnetic diffusivity  . Both the velocity and magnetic field are considered to be incompressible, so
. Both the velocity and magnetic field are considered to be incompressible, so  and
and  .
.
The fluid is confined in a cylinder of length  with its axis oriented along the z-axis. The ends of the cylinder are treated as periodic. The cross-section of the cylinder in the x–y plane is either a circle of radius 1 or an ellipse with major radius 1 along the x-axis and minor radius
with its axis oriented along the z-axis. The ends of the cylinder are treated as periodic. The cross-section of the cylinder in the x–y plane is either a circle of radius 1 or an ellipse with major radius 1 along the x-axis and minor radius  along the y-axis corresponding to an eccentricity of
along the y-axis corresponding to an eccentricity of  . No-slip (and non-penetration) boundary conditions are imposed on the velocity field. A helical forcing is imposed in the boundary conditions for
. No-slip (and non-penetration) boundary conditions are imposed on the velocity field. A helical forcing is imposed in the boundary conditions for  where the normal component is set to zero, the z-component is set to B0, and the poloidal component is set to Bc. This corresponds to the boundary conditions for the magnetic field following a helix along the wall, as illustrated in figure 1. We define the wrapping number q to be the number of rotations achieved by a magnetic streamline following the boundary conditions between z = 0 and
where the normal component is set to zero, the z-component is set to B0, and the poloidal component is set to Bc. This corresponds to the boundary conditions for the magnetic field following a helix along the wall, as illustrated in figure 1. We define the wrapping number q to be the number of rotations achieved by a magnetic streamline following the boundary conditions between z = 0 and  , and we choose
, and we choose  pairs which provide integral values of q for the simulations in this paper. It was shown in Shan and Montgomery (1993a, 1993b) that the instability of the current setup is determined by two parameters: the Hartmann number and the pinch-ratio. The Hartmann number was chosen proportional to the axial magnetic field, and the pinch-ratio is proportional to the wrapping number. Our description in terms of B0 and q is thus equivalent to the previous investigations.
pairs which provide integral values of q for the simulations in this paper. It was shown in Shan and Montgomery (1993a, 1993b) that the instability of the current setup is determined by two parameters: the Hartmann number and the pinch-ratio. The Hartmann number was chosen proportional to the axial magnetic field, and the pinch-ratio is proportional to the wrapping number. Our description in terms of B0 and q is thus equivalent to the previous investigations.
Figure 1. Sketch of the flow configuration: a conducting fluid in a cylinder is forced with a helical magnetic field imposed at the boundary.
Download figure:
Standard image High-resolution imageFigure 2. Schematic of fluid domain  and penalised domain
and penalised domain  in computational domain
in computational domain  .
.
Download figure:
Standard image High-resolution imageThe magnetic field is initialized to a linear profile that matches the boundary conditions. The velocity field is set to an uncorrelated Gaussian solenoidal random field with kinetic energy of the order 10−7.
2.2. Numerical method
The numerical method used for the simulations we studied is a Fourier pseudospectral method, with boundary conditions implemented via the penalisation method. A detailed description of the code and its validation can be found in Morales et al (2014).
The cylinder is immersed in a computational domain consisting of a periodic box of dimensions  , which we denote Ω. The fluid domain is denoted
, which we denote Ω. The fluid domain is denoted  , with the wall domain (also called solid domain) denoted
, with the wall domain (also called solid domain) denoted  , where
, where  , and
, and  . Let χ be the characteristic function for
. Let χ be the characteristic function for  . For the velocity, on which we impose homogeneous Dirichlet boundary conditions, we add
. For the velocity, on which we impose homogeneous Dirichlet boundary conditions, we add  to the right-hand side of (equation 1), where η is the penalisation parameter. We determine P by first computing the nonlinear source term
to the right-hand side of (equation 1), where η is the penalisation parameter. We determine P by first computing the nonlinear source term  and solving the Poisson equation
and solving the Poisson equation  . Substituting the resulting pressure gradient into (equation 1) enforces
. Substituting the resulting pressure gradient into (equation 1) enforces  .
.
For the magnetic field, we first find the penalisation field  which matches the helical-forcing boundary conditions on
which matches the helical-forcing boundary conditions on  and which is solenoidal in
and which is solenoidal in  . A method for generating this field is given in the
. A method for generating this field is given in the  by adding
by adding  to (equation 2). In order to ensure that
to (equation 2). In order to ensure that  , we compute
, we compute  and project
and project  onto the solenoidal manifold via a Helmholtz projection, which removes any divergence introduced by the penalisation term. Note that the penalisation field is itself solenoidal; this implies that the only source of divergence is due to the presence of
onto the solenoidal manifold via a Helmholtz projection, which removes any divergence introduced by the penalisation term. Note that the penalisation field is itself solenoidal; this implies that the only source of divergence is due to the presence of  in the penalisation term. A detailed validation of the penalisation method to impose tangential forcing at the boundary can be found in Morales et al (2014) for Taylor–Couette flow. In contrast to (Morales et al 2012), we penalise the magnetic field in the entire computational domain in order to avoid discontinuities in the nonlinear source term.
in the penalisation term. A detailed validation of the penalisation method to impose tangential forcing at the boundary can be found in Morales et al (2014) for Taylor–Couette flow. In contrast to (Morales et al 2012), we penalise the magnetic field in the entire computational domain in order to avoid discontinuities in the nonlinear source term.
The resulting equations are advanced in time in Fourier space using a second-order Adams–Bashforth method using an integrating factor for the diffusive terms. The time-step dt is restricted by the CFL condition (with a coefficient of 0.1) and the penalisation stability condition (Kolomenskiy and Schneider 2009) which imposes  . Laminar simulations were performed with 1283 Fourier modes while turbulent simulations were performed with 2563 modes. After dealiasing, 853 or 1713 degrees of freedom remained. The penalisation parameter η was chosen to be 5 × 10−4. It was verified that the results are consistent with those obtained using a resolution of 2563 and/or using
. Laminar simulations were performed with 1283 Fourier modes while turbulent simulations were performed with 2563 modes. After dealiasing, 853 or 1713 degrees of freedom remained. The penalisation parameter η was chosen to be 5 × 10−4. It was verified that the results are consistent with those obtained using a resolution of 2563 and/or using  .
.
3. Circular cross-section with constant axial forcing
Let us first consider a cylinder with circular cross-section. The kinetic energy of the fluid is initially low, and, after a short time (a few Alfvénic time units, depending on the boundary forcing) the kinetic energy grows exponentially with no change in topology, which is consistent with the linear instability of helical modes as described in Shan et al (1991), before reaching a new steady state. In certain cases (low wrapping numbers / boundary forcing magnitude) this does not occur, and the kinetic energy is essentially zero for the duration of the simulation. Example kinetic energy and kinetic energy dissipation curves are shown in figure 3.
Figure 3. Kinetic energy as a function of time (left) and dissipation of kinetic energy as a function of time (right) for simulations in circular geometry with B0 = 4.5 and  (red, long-dashed),
(red, long-dashed),  (blue, short-dashed),
(blue, short-dashed),  (green, solid).
(green, solid).
Download figure:
Standard image High-resolution imageWe set B0 = 4.5 and vary Bc so that integral values of wrapping numbers q are achieved. For q = 1 no flow is observed. At q = 2 ( ) we observe a helical structure in the velocity field consisting of two pairs of helices, as shown in figure 4. With these forcing parameters, the velocity modes have the same wrapping number as the boundary forcing of the magnetic field, which is also observed with wrapping number 3 (
) we observe a helical structure in the velocity field consisting of two pairs of helices, as shown in figure 4. With these forcing parameters, the velocity modes have the same wrapping number as the boundary forcing of the magnetic field, which is also observed with wrapping number 3 ( ). At wrapping number 4, the structure begins to break down, and is replaced with a helical dipole at q = 5 (
). At wrapping number 4, the structure begins to break down, and is replaced with a helical dipole at q = 5 ( ), with wavenumber 2 in the axial direction, as shown in figure 5. This low-order mode, which resembles the minimal dissipation mode as in Montgomery et al (1989), endures even at q = 20 (see figure 6), at which point the velocity field in the z-direction is disordered and exhibits a full spectrum, as shown in figure 7.
), with wavenumber 2 in the axial direction, as shown in figure 5. This low-order mode, which resembles the minimal dissipation mode as in Montgomery et al (1989), endures even at q = 20 (see figure 6), at which point the velocity field in the z-direction is disordered and exhibits a full spectrum, as shown in figure 7.
Figure 4. Axial velocity profile for wrapping number 2 with  in a circular geometry. Left: the two-dimensional cut is taken at z = 4. Right: isosurfaces of uz at
in a circular geometry. Left: the two-dimensional cut is taken at z = 4. Right: isosurfaces of uz at  , which correspond to isocontours in the left image. The poloidal wavenumber of the helical structure is 2, and the axial wavenumber is 1, i.e., the
, which correspond to isocontours in the left image. The poloidal wavenumber of the helical structure is 2, and the axial wavenumber is 1, i.e., the  mode dominates.
mode dominates.
Download figure:
Standard image High-resolution imageFigure 5. Axial velocity profile for wrapping number 5 with  in a circular geometry. Left: two-dimensional cut taken at z = 4. Right: isosurfaces at
in a circular geometry. Left: two-dimensional cut taken at z = 4. Right: isosurfaces at  , showing a
, showing a  mode.
mode.
Download figure:
Standard image High-resolution imageFigure 6. Axial velocity profile for wrapping number 20 with  in a circular geometry at t = 20. Left: two-dimensional cut taken at z = 4. Right: isosurfaces at
in a circular geometry at t = 20. Left: two-dimensional cut taken at z = 4. Right: isosurfaces at  , showing a central
, showing a central  mode away from the boundary. An animation can be found in the supplementary material.
mode away from the boundary. An animation can be found in the supplementary material.
Download figure:
Standard image High-resolution imageFigure 7. Power spectrum of the axial velocity (left) and axial magnetic field (right) at x = 0,  for the simulations shown in figure 4 (blue, dashed line) and figure 6 (green, solid line).
for the simulations shown in figure 4 (blue, dashed line) and figure 6 (green, solid line).
Download figure:
Standard image High-resolution image4. Circular cross-section with varying wrapping number and axial field
In the previous section, we increased forcing by increasing the wrapping number to explore the effect on the topology of the flow. In order to understand the individual roles of forcing and wrapping number, we also perform a number of simulations with wrapping number  and various forcing amplitudes.
and various forcing amplitudes.
For wrapping number 1, we observe the formation of structures first at forcing amplitude  , consisting of two helical structures of opposite-signed axial velocity and axial wavenumber 1, matching the forcing wrapping number. This structure is also present for
, consisting of two helical structures of opposite-signed axial velocity and axial wavenumber 1, matching the forcing wrapping number. This structure is also present for  , and exhibits decreasing regularity as the forcing parameter increased. For wrapping number 2, self-organization occurs at lower forcing values, first appearing at
, and exhibits decreasing regularity as the forcing parameter increased. For wrapping number 2, self-organization occurs at lower forcing values, first appearing at  , at which point we observe three helical pairs, as shown in figure 8. The structure of the flow becomes increasingly complex as
, at which point we observe three helical pairs, as shown in figure 8. The structure of the flow becomes increasingly complex as  increases, and an axial-wavenumber 1 mode appears at
increases, and an axial-wavenumber 1 mode appears at  , which persists up to
, which persists up to  . At wrapping number 3, we observed axial-wavenumber 1 helical structures at
. At wrapping number 3, we observed axial-wavenumber 1 helical structures at  , with two helical pairs at low forcing degenerating into less ordered (but still helical) structures as forcing magnitude increased. Finally, simulations with q = 4 show an axial wavenumber 2 helical pair at
, with two helical pairs at low forcing degenerating into less ordered (but still helical) structures as forcing magnitude increased. Finally, simulations with q = 4 show an axial wavenumber 2 helical pair at  , which persists up to
, which persists up to  . These results are summarized in figure 9, which may be compared to figure 1 in Shan and Montgomery (1993b), which shows the linearly unstable modes as a function of pinch ratio
. These results are summarized in figure 9, which may be compared to figure 1 in Shan and Montgomery (1993b), which shows the linearly unstable modes as a function of pinch ratio  and Hartmann number
and Hartmann number  in a parameter region different than given here.
in a parameter region different than given here.
Figure 8. Axial velocity profile for wrapping number 2 with  (
( ) in a circular geometry. Left: two-dimensional cut taken at z = 6. Right: isosurfaces at
) in a circular geometry. Left: two-dimensional cut taken at z = 6. Right: isosurfaces at  , showing a
, showing a  mode.
mode.
Download figure:
Standard image High-resolution imageFigure 9. Mode diagram of the flow topology of helical modes observed at a given wrapping number q and forcing amplitude  . Modes are (m,n), where m is the poloidal mode number and n is the toroidal (axial) mode number.
. Modes are (m,n), where m is the poloidal mode number and n is the toroidal (axial) mode number.
Download figure:
Standard image High-resolution image5. Alignment statistics
In figure 10 we show the probability density functions (pdfs) of the cosine of the angles between  ,
,  and
and  . These angles are chosen since they locally determine the strength of the Navier–Stokes nonlinearity, Lorentz force and magnetic field induction. Two cases are compared: a laminar one in which the velocity and magnetic field are stationary, and a turbulent multi-mode state. It is shown that already the laminar state shows non-trivial alignment properties. When the flow becomes turbulent the dynamics relax to a state in which in particular the magnetic field aligns more strongly with the velocity field compared to the laminar state. The
. These angles are chosen since they locally determine the strength of the Navier–Stokes nonlinearity, Lorentz force and magnetic field induction. Two cases are compared: a laminar one in which the velocity and magnetic field are stationary, and a turbulent multi-mode state. It is shown that already the laminar state shows non-trivial alignment properties. When the flow becomes turbulent the dynamics relax to a state in which in particular the magnetic field aligns more strongly with the velocity field compared to the laminar state. The  alignment becomes weaker and the
alignment becomes weaker and the  alignment does not dramatically increase or decrease in strength.
alignment does not dramatically increase or decrease in strength.
Figure 10. Probability distribution function for the cosine of the angle between  and
and  (red, solid),
(red, solid),  and
and  (blue, dashed), and
(blue, dashed), and  and
and  (green, dotted) at t = 30. The left figure shows values for a laminar flow with
(green, dotted) at t = 30. The left figure shows values for a laminar flow with  , and the right figure is for a turbulent flow with
, and the right figure is for a turbulent flow with  .
.
Download figure:
Standard image High-resolution imageSuch rapid local relaxation processes, in particular observed here for the  alignment have been observed previously in hydrodynamic (Pelz et al 1985) and MHD (Servidio et al 2008) turbulence. In particular in the latter work similar alignments as the ones in the present work are investigated in the case of isotropic MHD turbulence. It is observed in their results that the
alignment have been observed previously in hydrodynamic (Pelz et al 1985) and MHD (Servidio et al 2008) turbulence. In particular in the latter work similar alignments as the ones in the present work are investigated in the case of isotropic MHD turbulence. It is observed in their results that the  alignment becomes very strong. Furthermore, due to isotropy all their pdfs showed alignment–antialignment symmetry. This symmetry is lost in the pdfs of
alignment becomes very strong. Furthermore, due to isotropy all their pdfs showed alignment–antialignment symmetry. This symmetry is lost in the pdfs of  and
and  of our simulations due to the imposed helical character of the magnetic field. We do not think that the alignment in the turbulent case can be explained in an easy way. However, it was suggested by Kraichnan and Panda (1988) that the
of our simulations due to the imposed helical character of the magnetic field. We do not think that the alignment in the turbulent case can be explained in an easy way. However, it was suggested by Kraichnan and Panda (1988) that the  alignment observed in isotropic turbulence might be one representation of a more generic property of turbulent systems to suppress their nonlinearity. The rapid relaxation observed in the present work can also be thought to be an expression of this property.
alignment observed in isotropic turbulence might be one representation of a more generic property of turbulent systems to suppress their nonlinearity. The rapid relaxation observed in the present work can also be thought to be an expression of this property.
6. Elliptical cross section
Let us now consider a cylinder with elliptical cross section defined by  . As in the previous section, we keep the wrapping number constant and modify the forcing magnitude. The onset of kinetic energy growth occurs at much stronger forcing than in the circular case, with q = 1,
. As in the previous section, we keep the wrapping number constant and modify the forcing magnitude. The onset of kinetic energy growth occurs at much stronger forcing than in the circular case, with q = 1,  our first detection. At this point, the velocity field forms five pairs of opposite-sign helices, as shown in figure 11. As forcing is increased, 6 pairs are observed at
our first detection. At this point, the velocity field forms five pairs of opposite-sign helices, as shown in figure 11. As forcing is increased, 6 pairs are observed at  , and 5 pairs again at
, and 5 pairs again at  , 110, 120, and 130. As forcing amplitude is increased, the velocity field becomes increasingly concentrated at the border.
, 110, 120, and 130. As forcing amplitude is increased, the velocity field becomes increasingly concentrated at the border.
Figure 11. Axial velocity profile for wrapping number 1 with  (
( ) in an elliptical geometry. Left: two-dimensional cut at z = 4. Right: isosurfaces at
) in an elliptical geometry. Left: two-dimensional cut at z = 4. Right: isosurfaces at  , showing a
, showing a  mode.
mode.
Download figure:
Standard image High-resolution image7. Conclusion
In this article we studied the self-organization of the flow in a conducting fluid confined in a cylinder. The flow is forced by a helical magnetic field imposed via boundary conditions. This phenomenon was first explored by Shan et al (1991) using a purely spectral method for circular cross-sections with non-penetration boundary conditions. The simulations presented here used a large number of grid points, different parameter regimes, and were performed in cylinders with both circular and elliptical cross-sections. The penalisation technique can also be used in more general geometries. In cylinders of circular cross-section, various helical flows develop depending on the value of the wrapping number and forcing amplitude, tending toward a unique low-order mode at large values of the forcing parameters. This mode is present even when the fluid starts to exhibit turbulent dynamics. For the elliptical cross-section, the situation is different: a ring of vortices with poloidal mode number five or six forms and encloses a weak flow area. These vortices follow the topology of the imposed magnetic field. The magnitude of the forcing required to trigger this instability is much larger than for circular cases. For further work, it would be interesting to study the flow for larger ranges of Hartman number and pinch ratio, and to investigate the influence of the eccentricity of the ellipse on the topology of the flows obtained. Indeed, these first results in cylinders with non-circular cross-section reveal the significant influence of the shape on the modes which are excited. This observation might have important implications for the control of RFP fusion reactors, where the shape and frequency of the helically extended modes determine the quality of the plasma confinement. Even though in realistic RFP simulations the strong temperature gradient will have an important influence on the dynamics, already the isothermal visco-resistive MHD description is shown to reproduce a number of key features of the dynamics in Bonfiglio et al (2013).
Acknowledgments
This work was supported by the contract SiCoMHD (ANR-Blanc 2011-045), with simulations performed on IDRIS under project 91664 and made use of the HPC resources of Aix-Marseille Université financed by the project Equip@Meso (ANR-10-EQPX-29-01) of the program 'Investissements dʼAvenir' supervised by the ANR.
Appendix.: Numerical method for producing a solenoidal penalisation field
Let  be the computational, fluid, and solid domains, respectively, with
be the computational, fluid, and solid domains, respectively, with  . Given a Dirichlet boundary condition on
. Given a Dirichlet boundary condition on  represented by
represented by  such that
such that

where  is the normal vector on
is the normal vector on  . We wish to extend
. We wish to extend  to a sufficiently regular function
to a sufficiently regular function  on the entire computational domain
on the entire computational domain  such that
such that  . In order to find
. In order to find  numerically, we introduce a pseudo-time
numerically, we introduce a pseudo-time  and time-step the equation
and time-step the equation

where  is a diffusion parameter,
is a diffusion parameter,  is the characteristic function for
is the characteristic function for  and we call
and we call  the pseudo-time penalisation parameter. For the simulations in this paper, we chose
the pseudo-time penalisation parameter. For the simulations in this paper, we chose  , and we used an adaptive 1st/2nd order embedded Runge–Kutta time-integrator and a pseudospectral method in space, projecting
, and we used an adaptive 1st/2nd order embedded Runge–Kutta time-integrator and a pseudospectral method in space, projecting  onto the solenoidal manifold via a Helmholtz decomposition after each time-step. The time-stepping in
onto the solenoidal manifold via a Helmholtz decomposition after each time-step. The time-stepping in  is stopped when
is stopped when

where η is the penalisation parameter used to advance the fluid. This is to say that the maximum error between the penalisation field  and the desired value
and the desired value  on the boundary is less than one fifth the error expected from the penalisation term used in time-stepping the fluid. Since the boundary conditions obey the compatibility condition (equation A.1), the resulting field is consistent with a solenoidal field and should not be affected by projection onto the solenoidal manifold. Moreover, the stopping condition (inequality A.3) is satisfied only when the resulting penalisation field closely matches the boundary conditions.
on the boundary is less than one fifth the error expected from the penalisation term used in time-stepping the fluid. Since the boundary conditions obey the compatibility condition (equation A.1), the resulting field is consistent with a solenoidal field and should not be affected by projection onto the solenoidal manifold. Moreover, the stopping condition (inequality A.3) is satisfied only when the resulting penalisation field closely matches the boundary conditions.
The stop condition (A.3) implies that the error in the boundary conditions is sub-leading-order, and the use of a Helmholtz decomposition provides a penalisation field which is divergence-free up to machine precision. The choice of  determines the regularity of the field and the number of time-steps required for condition (A.3) to be achieved.
determines the regularity of the field and the number of time-steps required for condition (A.3) to be achieved.












